There are various definitions of the term decision tree. Most commonly, a decision tree provides a representation of the process of judging the class of a given data instance or record from the root node down to some leaf node. As a major classification model, the decision tree induction builds a decision tree as a classification model using the input dataset and class label pairs. A decision tree can be applied to various combinations of the following attribute data types, but is not limited to, including nominal valued, categorical, numeric and symbolic data, and their mixture. The following list is an illustration of Hunt's decision tree definition. The Step #7 applies a selected attribute test condition to partition the records to smaller datasets.

The decision tree is popular for its simplicity and low computational effort compared to other algorithms. Here are some characteristics of the decision tree induction:
- The greedy strategy is usually applied to the decision tree.
- It infers a decision tree once upon the entire training dataset.
- The algorithm requires no parameters to obtain the classification model from the input dataset.
- Like many other tasks, finding an optimal decision tree is an NP-complete problem.
- The algorithm to build the decision tree enables construction of the decision tree quickly. Tree construction is efficient, even upon large datasets.
- It provides an expressive way for discrete-valued functions.
- It is robust while opposed to noise.
- Using a top-down, recursive partition, the divide-and-conquer strategy is applied to most of the decision tree algorithms.
- The size of the sample dataset usually decreases dramatically when traversed down the tree.
- A subtree can be replicated many times in the decision tree.
- The test condition usually contains only one attribute.
- The performance of decision tree algorithms is affected by the impurity measure.
It is time to consider the decision tree when the instances in the source dataset are describable by the attribute-value pair, and the target function has discrete values, while the training dataset possibly has some noise.
An example of a decision tree built with the input dataset in a table (classical play golf dataset) is shown in the following diagram. The decision tree is composed of three entities or concepts: the root node, the internal node, and the leaf node. The leaf is given a class label. Nodes other than the leaf conduct tests on the attribute set to determine which input data belongs to which branch (child) of the node.

Given a built decision tree, a test record can be classified easily. From the root node, apply the test condition of that node to the test record and go to the next node with the corresponding test result until a leaf, by which we can decide which class the test record belongs to, is reached.
Now there will be two issues. One is how to divide the training set as per a certain node while the decision induction tree grows according to a chosen test condition upon various attribute sets. This will be a question related to attribute selection measure, which are illustrated in the following section. The second but important issue is related to model overfitting.
There are two strategies for the termination of the growth of the limiting decision induction tree node. Using the naïve strategy, for a certain node, when all the data objects within a node are assigned to it belong to the same class or all records with the same attribute values; as a result, the node related will be assigned with the class label as the majority of training records within that node. The second strategy terminates the algorithm earlier, which is meant to avoid model overfitting and will be introduced in the tree pruning section.
The node can have more than two children or branches depending on the attribute test condition and the selected attribute. To split the node, attribute selection measures with various implementations are applied. Attribute selection measures within the same node may also vary for binary branches or multiway branches. Some common attribute selection measures are the following:
- Entropy: This concept is used in information theory to describe the impurity of an arbitrary collection of data. Given the target attribute class set with size of c, and
 as the proportion/probability of S belonging to class i, the definition is here, and the definition Gain is shown in the next point. Entropy always means how disordered a dataset is. The higher the value of entropy, the more the uncertainty shown by the source dataset.
The size and coverage of the training set assigned to a certain node affect the correctness of the following equations. The gain is better for those situations.
as the proportion/probability of S belonging to class i, the definition is here, and the definition Gain is shown in the next point. Entropy always means how disordered a dataset is. The higher the value of entropy, the more the uncertainty shown by the source dataset.
The size and coverage of the training set assigned to a certain node affect the correctness of the following equations. The gain is better for those situations.
- Gain:

- Gain Ratio: This is applied in the C4.5 classification algorithm using the following formula:

- Information Gain: The ID3 algorithm uses this statistical property to decide which attribute is selected to be tested at any node in the tree, and measures the association between inputs and outputs of the decision tree.
With the concept of information gain, the definition of a decision tree can be thought of in this way:
- A decision tree is a tree-structured plan that uses a set of attribute tests to predict output
- To decide which attribute should be tested first, simply find the one with the highest information gain
- It, then, recurs
- Gini Index: It is used in the CART classification algorithm. The Gini index for a specific split point is calculated using the following equation. It is used to gauge the purity of the split point.

- Split Info:
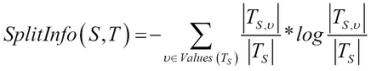
The initial decision tree is often built with many branches reflecting outliers or noise, which are also common causes of model overfitting. Usually, the direct consequent in tree pruning is needed for the after-dealt of decision tree aiming, which is required for classifying higher accuracy or lower error rates. The two types of pruning in production are as follows:
- Post-pruning: This approach is to perform tree pruning after the tree grows to the maximum form. The cost-complexity pruning algorithm used in CART and the pessimistic pruning in C4.5 are both examples of post-pruning.
- Pre-pruning: This is also known as the early stopping strategy, which avoids an over-matured tree generation, to stop the growth of a tree earlier using additional restrictions, such as a threshold.
Repetition and replication are the two major factors that make decision trees unreasonably large and inefficient.
Here is the pseudocode of the general decision induction tree algorithm:

Another variety of the algorithm is described here, with input parameters as follows:
- D denotes the training data
-
The leaf size is defined by

-
The leaf purity threshold is defined by

The output of the algorithm is a decision tree, as shown in the following screenshot:

Line 1 denotes the partition size. Line 4 denotes the stopping condition. Line 9 through line 17 try to get the two branches with the new split. Finally, line 19 applies the algorithm recursively on the two new subbranches to build the subtree. This algorithm is implemented with R in the following section.
The main function of the R code for the generic decision tree induction is listed as follows. Here data is the input dataset, c is the set of class labels, x is the set of attributes, and yita and pi have the same definitions as in the previous pseudocodes:
1 DecisionTree <- function(data,c,x,yita,pi){
2 result.tree <- NULL
3 if( StoppingCondition(data,c,yita,pi) ){
4 result.tree <- CreateLeafNode(data,c,yita,pi)
5 return(result.tree)
6 }
7
8 best.split <- GetBestSplit(data,c,x)
9 newdata <- SplitData(data,best.split)
10
11 tree.yes <- DecisionTree(newdata$yes,c,x,yita,pi)
12 tree.no <- DecisionTree(newdata$no,c,x,yita,pi)
13 result.tree <- CreateInternalNode(data,
14 best.split,tree.yes,tree.no)
15
16 result.tree
17 }One sample dataset is chosen to verify the generic decision tree induction algorithm, the weather dataset. It is from the R package Rattle, which contains 366 examples of 23 attributes, and one target or the class label. In the R language, weather is a data frame, which contains 366 observations of 24 variables. The details for the dataset can be retrieved with the following R code:
> Library(rattle) > str(weather)
