Clustering is defined as an unsupervised classification of a dataset. The objective of the clustering algorithm is to divide the given dataset (a set of points or objects) into groups of data instances or objects (or points) with distance or probabilistic measures. Members in the same groups are closer by distance or similarity or by other measures. In other words, maximize the similarity of the intracluster (internal homogeneity) and minimize the similarity of the intercluster (external separation).
In this chapter, you will learn how to implement the top algorithms for clusters with R; these algorithms are listed here:
- Search engine and the k-means algorithm
- Automatic abstracting of document texts and the k-medoids algorithm
- The CLARA algorithm
- CLARANS
- Unsupervised image categorization and affinity propagation clustering
- Web page clustering and spectral clustering
- News categorization and hierarchical clustering
A clustering algorithm is used for the preparation of further analysis, while the other objective is to understand the nature of the dataset. The most common clustering process is illustrated in the following diagram:
The key steps in this process include the following:
- Feature selection: This step chooses distinguished features from the original dataset
- Clustering algorithm design: This step designs an appropriate algorithm based on the currently available clustering algorithms, or it just builds one from scratch
- Cluster validation: This step evaluates the clusters and provides a degree of confidence about the result
- Result interpretation: This step gives an intrinsic idea of the input dataset
There are many categorization methods to categorize clustering algorithms; the major categories are partition-based methods, density-based methods, hierarchical methods, spectral methods, grid-based methods, and so on.
Every clustering algorithm has its limitations and best practices for certain conditions or datasets. Once an algorithm is chosen, the parameters and distance measures (only for some algorithms) related to that algorithm need careful consideration as well. Then, we will list the most popular clustering algorithms and their corresponding parallel versions (if available).
Here is the short list of clustering algorithms and their complexities:
|
Cluster algorithm |
Capability of tracking high dimensional data |
|---|---|
|
k-means |
No |
|
Fuzzy c-means |
No |
|
Hierarchical clustering |
No |
|
CLARA |
No |
|
CLARANS |
No |
|
BIRCH |
No |
|
DBSCAN |
No |
|
CURE |
Yes |
|
WaveCluster |
No |
|
DENCLUE |
Yes |
|
FC |
Yes |
|
CLIQUE |
Yes |
|
OptiGrid |
Yes |
|
ORCLUS |
Yes |
The difficulties or targets in another aspect of clustering algorithms are the arbitrary shape of clusters, large volume of datasets, high-dimensional datasets, insensitivity to noise or outlier, low reliance to user-defined parameters, capability of dealing with new data without learning after the initial learning or clustering, sensitivity to the intrinsic, or nature of the number of clusters, nice data visualization, and application to both numeric or nominal data types.
The general process of partition-based clustering is iterative. The first step defines or chooses a predefined number of representatives of the cluster and updates the representative after each iteration if the measure for the clustering quality has improved. The following diagram shows the typical process, that is, the partition of the given dataset into disjoint clusters:
The characteristics of partition-based clustering methods are as follows:
- The resulting clusters are exclusive in most of the circumstances
- The shape of the clusters are spherical, because of most of the measures adopted are distance-based measures
- The representative of each cluster is usually the mean or medoid of the corresponding group (cluster) of points
- A partition represents a cluster
- These clusters are applicable for small-to-medium datasets
- The algorithm will converge under certain convergence object functions, and the result clusters are often local optimum
The k-means clustering algorithm is basically a greedy approach that defines the centroid of each cluster with its mean value. It is efficient for dealing with a large dataset. The k-means algorithm is a kind of exclusive clustering algorithm in which data is clustered in an exclusive way, and one object only belongs to, at the most, one group or cluster. It is also a type of partitional clustering algorithm in which clusters are created in one step, in contrast to a couple of steps.
The value of k is often determined by the domain knowledge, the dataset, and so on. At the start, k objects in the initial dataset D (the size of D is n, where 
) are randomly selected as the initial centers for the initial k clusters. In the iteration of the k-means algorithm, each object is assigned to the most similar or closest (various measures are used for distance or similarity) cluster (mean). Once the iteration ends, the mean for each cluster is updated or relocated. The k-means algorithm performs as much iteration as possible until there is no change that the clusters get from the previous clustering.
The quality of the specific cluster of the clustering algorithm is measured by various merits. One of them is formulated in the following equation. This is within the cluster variation measure, where 
stands for the centroid of the cluster 
. Here, k is the number of clusters, whereas 
represents the Euclidean distance of the two points. The minimum value of E is the needed value and depicts the best quality clusters. This evaluation or assessing objective function serves as the ideal one, though not practical for concrete problems. The k-means algorithm provides easy methods for an approximate-to-ideal value. The k-means algorithm is also known as the squared error-based clustering algorithm.
In practice, the k-means algorithm can run several times with a different initial set of centroids to find a relatively better result.
The varieties of the k-means clustering algorithm are designed with different solutions for the selection of initial k centroids or means. The similarity or dissimilarity is measured, and the way to calculate the means is established.
The shortages of the k-means clustering method are listed as follows:
- The means of clusters must be defined with a function
- It is only applicable to numeric data type
- The value of k needs to be predefined by users, and it is difficult
The input parameters for a dual SVM algorithm is as follows:
- D, which is the set of training objects
- K
These parameters are used as depicted in the summarized pseudocodes of the k-means clustering algorithm given as follows:
This algorithm is a variant of the k-means algorithm; it can deal with categorical data types and large datasets. It can be integrated with the k-means method to deal with the clustering of the dataset that contains all data types. The algorithm is mentioned as follows:
Take a look at the ch_05_kmeans.R, ch_05_kernel_kmeans.R, and ch_05_kmedoids.R R code files from the bundle of R code for the previously mentioned algorithms. The code can be tested using the following commands:
> source("ch_05_kmeans.R") > source("ch_05_kernel_kmeans.R") > source("ch_05_kmedoids.R")
Along with the nonstop accumulation of Internet documents, the difficulties in finding some useful information keeps increasing. To find information in these documents or web pages or from the Web, four search methodologies are provided to us:
- The unassisted keyword search
- The assisted keyword search
- The directory-based search
- The query-by-example search
Web page clustering is an important preprocessing step to web data mining, which is one solution among the many possible solutions. The document clustering occurs in the progress of IR and text clustering. Many web clustering criteria are provided, such as the semantic, the structure, the usage-based criteria, and so on. Domain knowledge plays an important role in web page clustering.
Term Frequency-Inverse Document Frequency (TF-IDF) is applied during the preprocessing of the document dataset. One modeling method to represent a data instance for document clustering is the vector-space model. Given a term space, each dimension with a specific term in the documents and any document in the original document dataset can be represented by a vector, as depicted in the following equation. This definition implies that mostly, frequently used terms play an important role in the document:
Each value in a dimension denotes the frequency of the term that labels the dimension appearing in the document. For simplicity, the vector needs to be normalized as a unit length before processing it further, the stop words should be removed, and so on. As a potential and popular solution, the TF often weighs every term using the inverse document frequency among the document datasets. The inverse document frequency is denoted by the following formula in which n is the dataset size, and 
is the document's number that contains the term, 
:
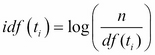
Given the definition of inverse document frequency, there is another popular definition of the vector model to denote a document in the document collection for further processing using a clustering algorithm; 
is the frequency of term in the document 
:
The measures used in the document clustering are versatile and tremendous. Cosine method is one among them, and we will use the vector dot production in the equation while the corresponding centroid is defined as c in the successive equation:
Reuters-21578 is one publicly-available document dataset for further research. TREC-5, 6, and 7 are also open source datasets.
With this measure definition, the k-means algorithm is used for web page clustering, as it displays its efficiency and always acts as a component for a practical web search engine.