We have seen that box plots are a great way of comparing the distribution of a continuous variable across different categories. As you might expect, box plots are very easy to produce using ggplot2. The following snippet produces the box-and-whisker plot that we saw earlier, depicting the relationship between the petal lengths of the different iris species in the iris dataset:

  > library(ggplot)
  > qplot(Species, Petal.Length, data=iris, geom="boxplot", 
  +       fill=Species)

First, we specify the variable on the x-axis (the iris species) and then the continuous variable on the y-axis (the petal length). Finally, we specify that we are using the iris dataset, that we want a box plot, and that we want to fill the boxes with different colors for each iris species.

Another fun way of comparing distributions between the different categories is by using an overlapping density plot:

  > qplot(Petal.Length, data=iris, geom="density", alpha=I(.7), 
  +       fill=Species)

Here we need only specify the continuous variable, since the fill parameter will break down the density plot by species. The alpha parameter adds transparency to show more clearly the extent to which the distributions overlap.

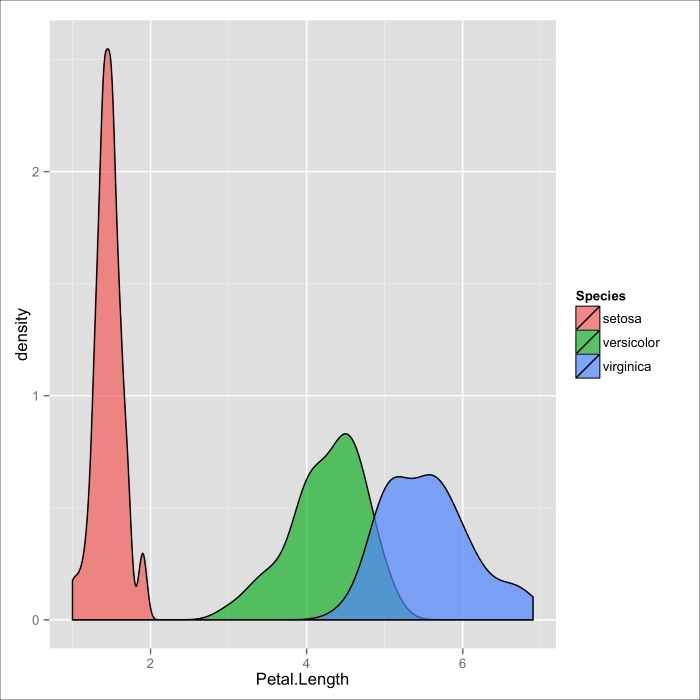
Figure 3.9: Overlapping density plot of petal length of iris flowers across species

If it is not the distribution you are trying to compare but some kind of single-value statistic (like standard deviation or sample counts), you can use the by function to get that value across all categories, and then build a bar plot where each category is a bar, and the heights of the bars represent that category's statistic. For the code to construct a bar plot, refer back to the last section in Chapter 1, RefresheR.

The visualization of categorical data is a grossly understudied domain and, in spite of some fairly powerful and compelling visualization methods, these techniques remain relatively unpopular.

My favorite method for graphically illustrating contingency tables is to use a mosaic plot. To make mosaic plots, we will need to install and load the VCD (Visualizing Categorical Data) package:

  > # install.packages("vcd")
  > library(vcd)
  >
  > ucba <- data.frame(UCBAdmissions)
  > mosaic(Freq ~ Gender + Admit, data=ucba,
  +        shade=TRUE, legend=FALSE)

Figure 3.10: A mosaic plot of the UCBAdmissions dataset (across all departments)

The first argument to the mosaic function is a formula. This formula is meant to be read as: display frequency broken down by gender and whether the applicant was admitted. shade=TRUE adds a little life to the plot by adding colors to the boxes. The colors are actually very meaningful, as is the legend we opted not to show with the final parameter—but its meaning is beyond the scope of this section.

The mosaic plot represents each cell of a 2x2 contingency table as a tile; the area of the box is proportional to the number of observations in that cell. From this plot, we can easily tell that (a) more men applied to UCB than women, (b) more applicants were rejected than accepted, and (c) women were rejected at a higher proportion than male applicants.

You remember how this was misleading, right? Let's look at the mosaic plot for only department A:

  > mosaic(Freq ~ Gender+Admit, data=ucba[ucba$Dept=="A",],
  +        shade=TRUE, legend=FALSE)

Figure 3.11: A mosaic plot of the UCBAdmissions dataset for department A

Hopefully, this plot makes the treachery of Simpson's paradox more apparent. Notice how there were far fewer female applicants than males, but the admission rates for the female applicants were much higher. Try visualizing the mosaic plots for the other departments by yourself!

The canonical way of displaying relationships between two continuous variables is via scatterplots. The scatterplot for the women's heights and weights that we saw earlier in this chapter was produced with the following R code snippet:

  > qplot(height, weight, data=women, geom="point")

Whether you put height and weight first depends on which variable you want tied to the x-axis.

What about that fancy regression line?!, you ask frantically. ggplot2 gracefully provides this feature with just a few extra characters. The scatterplot of the relationship between the weight of a car and its miles per gallon was produced as follows:

  > qplot(wt, mpg, data=mtcars, geom=c("point", "smooth"),
  +       method="lm", se=FALSE)'

Here, we are specifying that we want two kinds of geometric objects, point and smooth. The latter is responsible for the regression line. method="lm" tells qplot that we want to use a linear model to create the trend line.

If we leave out the method, ggplot2 will choose a method automatically; in this case, it would default to a method of drawing a non-linear trend line called LOESS:

  > qplot(wt, mpg, data=mtcars, geom=c("point", "smooth"), se=FALSE)

Figure 3.12: A scatterplot of the relationship between the weight of a car and its miles per gallon, and a trend-line smoothed with LOESS

The se=FALSE directive instructs ggplot2 not to plot the estimates of the error. We will get to what this means in a later chapter.

Finally, there is an excellent way to visualize correlation matrices like the one we saw with the iris dataset in the section Comparing multiple correlations. To do this, we have to install and load the corrgram package as follows:

  > # install.packages("corrgram")
  > library(corrgram)
  >
  > corrgram(iris, lower.panel=panel.conf, upper.panel=panel.pts)

Figure 3.13: A corrgram of the iris data set's continuous variables

With corrgrams, we can exploit the fact the correlation matrices are symmetrical by packing in more information. On the lower left panel, we have the Pearson correlation coefficients (never mind the small ranges beneath each coefficient for now). Instead of repeating these coefficients for the upper right panel, we can show a small scatterplot there instead.

We aren't limited to showing the coefficients and scatterplots in our corrgram, though; there are many other options and configurations available:

  > corrgram(iris, lower.panel=panel.pie, upper.panel=panel.pts,
  +          diag.panel=panel.density,
  +          main=paste0("corrgram of petal and sepal ",
  +                      "measurements in iris data set"))

Figure 3.14: Another corrgram of the iris dataset's continuous variables

Notice that this time, we can overlay a density plot wherever there is a variable name (on the diagonal) —just to get a sense of the variables' shapes. More saliently, instead of text coefficients, we have pie charts in the lower-left panel. These pie charts are meant to graphically depict the strength of the correlations.

If the color of the pie is blue (or any shade thereof), the correlation is positive; the bigger the shaded area of the pie, the stronger the magnitude of the correlation. If, however, the color of the pie is red or a shade of red, the correlation is negative, and the amount of shading on the pie is proportional to the magnitude of the correlation.

To top it all off, we added the main parameter to set the title of the plot. Note the use of paste0 so that I could split the title up into two lines of code.

To get a better sense of what corrgram is capable of, you can view a live demonstration of examples if you execute the following at the prompt:

  > example(corrgram)