 Industry-specific investment
by Ágnes Vidovics-Dancs, Kata Váradi, Tamás Vadász, Ágnes Tuza, Balázs Árpád Szucs,
R: Data Analysis and Visualization
Industry-specific investment
by Ágnes Vidovics-Dancs, Kata Váradi, Tamás Vadász, Ágnes Tuza, Balázs Árpád Szucs,
R: Data Analysis and Visualization
- R: Data Analysis and Visualization
- Table of Contents
- R: Data Analysis and Visualization
- I. Module 1: Data Analysis with R
- 1. RefresheR
- 2. The Shape of Data
- 3. Describing Relationships
- 4. Probability
- 5. Using Data to Reason About the World
- 6. Testing Hypotheses
- 7. Bayesian Methods
- 8. Predicting Continuous Variables
- 9. Predicting Categorical Variables
- 10. Sources of Data
- 11. Dealing with Messy Data
- 12. Dealing with Large Data
- 13. Reproducibility and Best Practices
- II. Module 2: R Graphs
- 1. R Graphics
- 2. Basic Graph Functions
- Introduction
- Creating basic scatter plots
- Creating line graphs
- Creating bar charts
- Creating histograms and density plots
- Creating box plots
- Adjusting x and y axes' limits
- Creating heat maps
- Creating pairs plots
- Creating multiple plot matrix layouts
- Adding and formatting legends
- Creating graphs with maps
- Saving and exporting graphs
- 3. Beyond the Basics – Adjusting Key Parameters
- Introduction
- Setting colors of points, lines, and bars
- Setting plot background colors
- Setting colors for text elements – axis annotations, labels, plot titles, and legends
- Choosing color combinations and palettes
- Setting fonts for annotations and titles
- Choosing plotting point symbol styles and sizes
- Choosing line styles and width
- Choosing box styles
- Adjusting axis annotations and tick marks
- Formatting log axes
- Setting graph margins and dimensions
- 4. Creating Scatter Plots
- Introduction
- Grouping data points within a scatter plot
- Highlighting grouped data points by size and symbol type
- Labeling data points
- Correlation matrix using pairs plots
- Adding error bars
- Using jitter to distinguish closely packed data points
- Adding linear model lines
- Adding nonlinear model curves
- Adding nonparametric model curves with lowess
- Creating three-dimensional scatter plots
- Creating Quantile-Quantile plots
- Displaying the data density on axes
- Creating scatter plots with a smoothed density representation
- 5. Creating Line Graphs and Time Series Charts
- Introduction
- Adding customized legends for multiple-line graphs
- Using margin labels instead of legends for multiple-line graphs
- Adding horizontal and vertical grid lines
- Adding marker lines at specific x and y values using abline
- Creating sparklines
- Plotting functions of a variable in a dataset
- Formatting time series data for plotting
- Plotting the date or time variable on the x axis
- Annotating axis labels in different human-readable time formats
- Adding vertical markers to indicate specific time events
- Plotting data with varying time-averaging periods
- Creating stock charts
- 6. Creating Bar, Dot, and Pie Charts
- Introduction
- Creating bar charts with more than one factor variable
- Creating stacked bar charts
- Adjusting the orientation of bars – horizontal and vertical
- Adjusting bar widths, spacing, colors, and borders
- Displaying values on top of or next to the bars
- Placing labels inside bars
- Creating bar charts with vertical error bars
- Modifying dot charts by grouping variables
- Making better, readable pie charts with clockwise-ordered slices
- Labeling a pie chart with percentage values for each slice
- Adding a legend to a pie chart
- 7. Creating Histograms
- Introduction
- Visualizing distributions as count frequencies or probability densities
- Setting the bin size and the number of breaks
- Adjusting histogram styles – bar colors, borders, and axes
- Overlaying a density line over a histogram
- Multiple histograms along the diagonal of a pairs plot
- Histograms in the margins of line and scatter plots
- 8. Box and Whisker Plots
- Introduction
- Creating box plots with narrow boxes for a small number of variables
- Grouping over a variable
- Varying box widths by the number of observations
- Creating box plots with notches
- Including or excluding outliers
- Creating horizontal box plots
- Changing the box styling
- Adjusting the extent of plot whiskers outside the box
- Showing the number of observations
- Splitting a variable at arbitrary values into subsets
- 9. Creating Heat Maps and Contour Plots
- 10. Creating Maps
- 11. Data Visualization Using Lattice
- Introduction
- Creating bar charts
- Creating stacked bar charts
- Creating bar charts to visualize cross-tabulation
- Creating a conditional histogram
- Visualizing distributions through a kernel-density plot
- Creating a normal Q-Q plot
- Visualizing an empirical Cumulative Distribution Function
- Creating a boxplot
- Creating a conditional scatter plot
- 12. Data Visualization Using ggplot2
- 13. Inspecting Large Datasets
- 14. Three-dimensional Visualizations
- 15. Finalizing Graphs for Publications and Presentations
- Introduction
- Exporting graphs in high-resolution image formats – PNG, JPEG, BMP, and TIFF
- Exporting graphs in vector formats – SVG, PDF, and PS
- Adding mathematical and scientific notations (typesetting)
- Adding text descriptions to graphs
- Using graph templates
- Choosing font families and styles under Windows, Mac OS X, and Linux
- Choosing fonts for PostScripts and PDFs
- III. Module 3: Learning Data Mining with R
- 1. Warming Up
- 2. Mining Frequent Patterns, Associations, and Correlations
- An overview of associations and patterns
- Market basket analysis
- Hybrid association rules mining
- Mining sequence dataset
- The R implementation
- High-performance algorithms
- 3. Classification
- Classification
- Generic decision tree induction
- High-value credit card customers classification using ID3
- Web spam detection using C4.5
- Web key resource page judgment using CART
- Trojan traffic identification method and Bayes classification
- Identify spam e-mail and Naïve Bayes classification
- Rule-based classification of player types in computer games and rule-based classification
- 4. Advanced Classification
- 5. Cluster Analysis
- 6. Advanced Cluster Analysis
- Customer categorization analysis of e-commerce and DBSCAN
- Clustering web pages and OPTICS
- Visitor analysis in the browser cache and DENCLUE
- Recommendation system and STING
- Web sentiment analysis and CLIQUE
- Opinion mining and WAVE clustering
- User search intent and the EM algorithm
- Customer purchase data analysis and clustering high-dimensional data
- SNS and clustering graph and network data
- 7. Outlier Detection
- Credit card fraud detection and statistical methods
- Activity monitoring – the detection of fraud involving mobile phones and proximity-based methods
- Intrusion detection and density-based methods
- Intrusion detection and clustering-based methods
- Monitoring the performance of the web server and classification-based methods
- Detecting novelty in text, topic detection, and mining contextual outliers
- Collective outliers on spatial data
- Outlier detection in high-dimensional data
- 8. Mining Stream, Time-series, and Sequence Data
- 9. Graph Mining and Network Analysis
- 10. Mining Text and Web Data
- IV. Module 4: Mastering R for Quantitative Finance
- 1. Time Series Analysis
- 2. Factor Models
- 3. Forecasting Volume
- 4. Big Data – Advanced Analytics
- 5. FX Derivatives
- 6. Interest Rate Derivatives and Models
- 7. Exotic Options
- A general pricing approach
- The role of dynamic hedging
- How R can help a lot
- A glance beyond vanillas
- Greeks – the link back to the vanilla world
- Pricing the Double-no-touch option
- Another way to price the Double-no-touch option
- The life of a Double-no-touch option – a simulation
- Exotic options embedded in structured products
- References
- 8. Optimal Hedging
- 9. Fundamental Analysis
- 10. Technical Analysis, Neural Networks, and Logoptimal Portfolios
- 11. Asset and Liability Management
- 12. Capital Adequacy
- 13. Systemic Risks
- V. Module 5: Machine Learning with R module
- 1. Introducing Machine Learning
- 2. Managing and Understanding Data
- R data structures
- Managing data with R
- Exploring and understanding data
- Exploring the structure of data
- Exploring numeric variables
- Measuring the central tendency – mean and median
- Measuring spread – quartiles and the five-number summary
- Visualizing numeric variables – boxplots
- Visualizing numeric variables – histograms
- Understanding numeric data – uniform and normal distributions
- Measuring spread – variance and standard deviation
- Exploring categorical variables
- Exploring relationships between variables
- 3. Lazy Learning – Classification Using Nearest Neighbors
- 4. Probabilistic Learning – Classification Using Naive Bayes
- 5. Divide and Conquer – Classification Using Decision Trees and Rules
- Understanding decision trees
- Example – identifying risky bank loans using C5.0 decision trees
- Understanding classification rules
- Example – identifying poisonous mushrooms with rule learners
- 6. Forecasting Numeric Data – Regression Methods
- Understanding regression
- Example – predicting medical expenses using linear regression
- Understanding regression trees and model trees
- Example – estimating the quality of wines with regression trees and model trees
- 7. Black Box Methods – Neural Networks and Support Vector Machines
- 8. Finding Patterns – Market Basket Analysis Using Association Rules
- 9. Finding Groups of Data – Clustering with k-means
- 10. Evaluating Model Performance
- 11. Improving Model Performance
- 12. Specialized Machine Learning Topics
- Working with proprietary files and databases
- Working with online data and services
- Working with domain-specific data
- Improving the performance of R
- Managing very large datasets
- Learning faster with parallel computing
- GPU computing
- Deploying optimized learning algorithms
- Building bigger regression models with biglm
- Growing bigger and faster random forests with bigrf
- Training and evaluating models in parallel with caret
- A. Reflect and Test Yourself Answers
- Module 1: Data Analysis with R
- Chapter 1: RefresheR
- Chapter 2: The Shape of Data
- Chapter 3: Describing Relationships
- Chapter 4: Probability
- Chapter 5: Using Data to Reason About the World
- Chapter 6: Testing Hypotheses
- Chapter 7: Bayesian Methods
- Chapter 8: Predicting Continuous Variables
- Chapter 9: Predicting Categorical Variables
- Chapter 10: Sources of Data
- Chapter 11: Dealing with Messy Data
- Chapter 12: Dealing with Large Data
- Module 2: R Graphs
- Chapter 1: R Graphics
- Chapter 2: Basic Graph Functions
- Chapter 3: Beyond the Basics – Adjusting Key Parameters
- Chapter 4: Creating Scatter Plots
- Chapter 5: Creating Line Graphs and Time Series Charts
- Chapter 6: Creating Bar, Dot, and Pie Charts
- Chapter 7: Creating Histograms
- Chapter 8: Box and Whisker Plots
- Chapter 9: Creating Heat Maps and Contour Plots
- Module 4: Mastering R for Quantitative Finance
- Module 5: Machine Learning with R
- Chapter 1: Introducing Machine Learning
- Chapter 2: Managing and Understanding Data
- Chapter 3: Lazy Learning – Classification Using Nearest Neighbors
- Chapter 4: Probabilistic Learning – Classification Using Naive Bayes
- Chapter 5: Divide and Conquer – Classification Using Decision Trees and Rules
- Chapter 6: Forecasting Numeric Data – Regression Methods
- Chapter 7: Black Box Methods – Neural Networks and Support Vector Machines
- Chapter 8: Finding Patterns – Market Basket Analysis Using Association Rules
- Module 1: Data Analysis with R
- B. Bibliography
- Index
Until this point, we considered the entire sample as one. It could be a logical decision to focus only on some industries. Note that choosing the right industry to invest should not be based on past performance pattern; we rather have to analyze comovements with global economic trends over a number of years, and then, based on our prediction for the coming periods, we should pick the one with the best outlook. This method helps you to determine the right weights of the industries in your portfolio, but then, you still need to select individual shares that may overperform the others.
Of course, once one given industry is selected, we may end up with different investment rules than those on the whole sample. So, we may further improve our investment performance by performing the previously shown steps for each industry separately.
At the same time, recall that the more specific you are in data selection (time period, industry, and firm size), the less likely will the strategy created show good performance on other samples or in the future. By increasing the degree of freedom of your strategy building (rerunning all statistical tests for subsamples), you make recommendations fit nearly perfectly to the given sample that may reflect the effects of a number of random events. As these random effects never occur again, adding more and more flexibility after a certain limit will actually worsen the end result.
For the sake of the example, we picked Communications. If we apply the decision-tree technique here, we would end up with the following figure. After that, we have to invest into firms that have seen their revenue growing by less than 21 percent but more than 1.31 percent during the last year, while the net fixed assets ratio was at least 8.06 percent:
d_comm <- d[d[,18] == "Communications",c(3:17,19)] vars <- colnames(d_comm) m <- length(vars) tree_formula <- paste(vars[m], paste(vars[-m], collapse = " + "), sep = " ~ ") library(rpart) tree <- rpart(formula = tree_formula, data = d_comm, maxdepth = 5 ,cp = 0.01, control = rpart.control(minsplit = 100)) tree <- prune(tree, cp = 0.006) par(xpd = T) plot(tree) text(tree, cex = .5, use.n = T, all = T) print(tree)
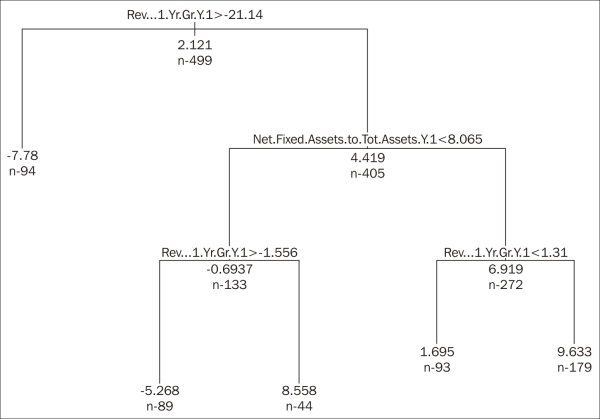
At the same time, building a strategy based on a general sample of a given period may end up overweighting certain industries that show great performance during the given year(s), while, of course, there is no guarantee that the coming years will also prefer the same sectors. So, after building our strategy, we should crosscheck whether there is a serious industry dependency behind that strategy.
A cross-table controlling for the connection of the industry and decision-tree-based investment strategy reveals that we heavily overweighted the Energy and Utilities sectors. The cluster-based strategy, at the same time, gives an extra weight to materials. The code for the latter is shown here:
cross <- table(d[,18], d$selected) colnames(cross) <- c("not selected", "selected") cross not selected selected Communications 488 11 Consumer Discretionary 1476 44 Consumer Staples 675 36 Energy 449 32 Financials 116 1 Health Care 535 37 Industrials 1179 53 Materials 762 99 Technology 894 7 Utilities 287 17 prop.table(cross) not selected selected Communications 0.0677966102 0.0015282023 Consumer Discretionary 0.2050569603 0.0061128091 Consumer Staples 0.0937760489 0.0050013893 Energy 0.0623784385 0.0044456794 Financials 0.0161155877 0.0001389275 Health Care 0.0743262017 0.0051403168 Industrials 0.1637954987 0.0073631564 Materials 0.1058627396 0.0137538205 Technology 0.1242011670 0.0009724924 Utilities 0.0398721867 0.0023617672
We may also be interested in how good our strategy performs across industries. For this, we should see the average TRS of firms chosen and not chosen for all the individual sectors. To create a table like this, we need to use the following command. The output illustrates how the decision-tree-based strategy performs (0 not selected, 1 selected):
t1 <- aggregate(d[ d$tree,19], list(d[ d$tree,18]), function(x) c(mean(x), median(x))) t2 <- aggregate(d[!d$tree,19], list(d[!d$tree,18]), function(x) c(mean(x), median(x))) industry_crosstab <- round(cbind(t1$x, t2$x),4) colnames(industry_crosstab) <- c("mean-1","median-1","mean-0","median-0") rownames(industry_crosstab) <- t1[,1] industry_crosstab mean-1 median-1 mean-0 median-0 Communications 10.4402 11.5531 1.8810 2.8154 Consumer Discretionary 15.9422 10.7034 2.7963 1.3154 Consumer Staples 14.2748 6.5512 4.5523 3.1839 Energy 17.8265 16.7273 5.6107 5.0800 Financials 33.3632 33.9155 5.4558 3.5193 Health Care 26.6268 21.8815 7.5387 4.6022 Industrials 29.2173 17.6756 6.5487 3.7119 Materials 22.9989 21.3155 8.4270 5.6327 Technology 43.9722 46.8772 7.4596 5.3433 Utilities 11.6620 11.1069 8.6993 7.7672
As shown in the preceding output, our strategy performs pretty well in all sectors; though in Consumer Staples, the median of the selected firms is somewhat near to that of not selected. In other cases, we may end up seeing that in some sectors, we do not get very good results, and the TRS of the chosen firms may even be lower than that of the other group. In this case, we would build a separate stock-selection model for those sectors where our model performed weaker.

-
No Comment