 Choosing a classifier
by Ágnes Vidovics-Dancs, Kata Váradi, Tamás Vadász, Ágnes Tuza, Balázs Árpád Szucs,
R: Data Analysis and Visualization
Choosing a classifier
by Ágnes Vidovics-Dancs, Kata Váradi, Tamás Vadász, Ágnes Tuza, Balázs Árpád Szucs,
R: Data Analysis and Visualization
- R: Data Analysis and Visualization
- Table of Contents
- R: Data Analysis and Visualization
- I. Module 1: Data Analysis with R
- 1. RefresheR
- 2. The Shape of Data
- 3. Describing Relationships
- 4. Probability
- 5. Using Data to Reason About the World
- 6. Testing Hypotheses
- 7. Bayesian Methods
- 8. Predicting Continuous Variables
- 9. Predicting Categorical Variables
- 10. Sources of Data
- 11. Dealing with Messy Data
- 12. Dealing with Large Data
- 13. Reproducibility and Best Practices
- II. Module 2: R Graphs
- 1. R Graphics
- 2. Basic Graph Functions
- Introduction
- Creating basic scatter plots
- Creating line graphs
- Creating bar charts
- Creating histograms and density plots
- Creating box plots
- Adjusting x and y axes' limits
- Creating heat maps
- Creating pairs plots
- Creating multiple plot matrix layouts
- Adding and formatting legends
- Creating graphs with maps
- Saving and exporting graphs
- 3. Beyond the Basics – Adjusting Key Parameters
- Introduction
- Setting colors of points, lines, and bars
- Setting plot background colors
- Setting colors for text elements – axis annotations, labels, plot titles, and legends
- Choosing color combinations and palettes
- Setting fonts for annotations and titles
- Choosing plotting point symbol styles and sizes
- Choosing line styles and width
- Choosing box styles
- Adjusting axis annotations and tick marks
- Formatting log axes
- Setting graph margins and dimensions
- 4. Creating Scatter Plots
- Introduction
- Grouping data points within a scatter plot
- Highlighting grouped data points by size and symbol type
- Labeling data points
- Correlation matrix using pairs plots
- Adding error bars
- Using jitter to distinguish closely packed data points
- Adding linear model lines
- Adding nonlinear model curves
- Adding nonparametric model curves with lowess
- Creating three-dimensional scatter plots
- Creating Quantile-Quantile plots
- Displaying the data density on axes
- Creating scatter plots with a smoothed density representation
- 5. Creating Line Graphs and Time Series Charts
- Introduction
- Adding customized legends for multiple-line graphs
- Using margin labels instead of legends for multiple-line graphs
- Adding horizontal and vertical grid lines
- Adding marker lines at specific x and y values using abline
- Creating sparklines
- Plotting functions of a variable in a dataset
- Formatting time series data for plotting
- Plotting the date or time variable on the x axis
- Annotating axis labels in different human-readable time formats
- Adding vertical markers to indicate specific time events
- Plotting data with varying time-averaging periods
- Creating stock charts
- 6. Creating Bar, Dot, and Pie Charts
- Introduction
- Creating bar charts with more than one factor variable
- Creating stacked bar charts
- Adjusting the orientation of bars – horizontal and vertical
- Adjusting bar widths, spacing, colors, and borders
- Displaying values on top of or next to the bars
- Placing labels inside bars
- Creating bar charts with vertical error bars
- Modifying dot charts by grouping variables
- Making better, readable pie charts with clockwise-ordered slices
- Labeling a pie chart with percentage values for each slice
- Adding a legend to a pie chart
- 7. Creating Histograms
- Introduction
- Visualizing distributions as count frequencies or probability densities
- Setting the bin size and the number of breaks
- Adjusting histogram styles – bar colors, borders, and axes
- Overlaying a density line over a histogram
- Multiple histograms along the diagonal of a pairs plot
- Histograms in the margins of line and scatter plots
- 8. Box and Whisker Plots
- Introduction
- Creating box plots with narrow boxes for a small number of variables
- Grouping over a variable
- Varying box widths by the number of observations
- Creating box plots with notches
- Including or excluding outliers
- Creating horizontal box plots
- Changing the box styling
- Adjusting the extent of plot whiskers outside the box
- Showing the number of observations
- Splitting a variable at arbitrary values into subsets
- 9. Creating Heat Maps and Contour Plots
- 10. Creating Maps
- 11. Data Visualization Using Lattice
- Introduction
- Creating bar charts
- Creating stacked bar charts
- Creating bar charts to visualize cross-tabulation
- Creating a conditional histogram
- Visualizing distributions through a kernel-density plot
- Creating a normal Q-Q plot
- Visualizing an empirical Cumulative Distribution Function
- Creating a boxplot
- Creating a conditional scatter plot
- 12. Data Visualization Using ggplot2
- 13. Inspecting Large Datasets
- 14. Three-dimensional Visualizations
- 15. Finalizing Graphs for Publications and Presentations
- Introduction
- Exporting graphs in high-resolution image formats – PNG, JPEG, BMP, and TIFF
- Exporting graphs in vector formats – SVG, PDF, and PS
- Adding mathematical and scientific notations (typesetting)
- Adding text descriptions to graphs
- Using graph templates
- Choosing font families and styles under Windows, Mac OS X, and Linux
- Choosing fonts for PostScripts and PDFs
- III. Module 3: Learning Data Mining with R
- 1. Warming Up
- 2. Mining Frequent Patterns, Associations, and Correlations
- An overview of associations and patterns
- Market basket analysis
- Hybrid association rules mining
- Mining sequence dataset
- The R implementation
- High-performance algorithms
- 3. Classification
- Classification
- Generic decision tree induction
- High-value credit card customers classification using ID3
- Web spam detection using C4.5
- Web key resource page judgment using CART
- Trojan traffic identification method and Bayes classification
- Identify spam e-mail and Naïve Bayes classification
- Rule-based classification of player types in computer games and rule-based classification
- 4. Advanced Classification
- 5. Cluster Analysis
- 6. Advanced Cluster Analysis
- Customer categorization analysis of e-commerce and DBSCAN
- Clustering web pages and OPTICS
- Visitor analysis in the browser cache and DENCLUE
- Recommendation system and STING
- Web sentiment analysis and CLIQUE
- Opinion mining and WAVE clustering
- User search intent and the EM algorithm
- Customer purchase data analysis and clustering high-dimensional data
- SNS and clustering graph and network data
- 7. Outlier Detection
- Credit card fraud detection and statistical methods
- Activity monitoring – the detection of fraud involving mobile phones and proximity-based methods
- Intrusion detection and density-based methods
- Intrusion detection and clustering-based methods
- Monitoring the performance of the web server and classification-based methods
- Detecting novelty in text, topic detection, and mining contextual outliers
- Collective outliers on spatial data
- Outlier detection in high-dimensional data
- 8. Mining Stream, Time-series, and Sequence Data
- 9. Graph Mining and Network Analysis
- 10. Mining Text and Web Data
- IV. Module 4: Mastering R for Quantitative Finance
- 1. Time Series Analysis
- 2. Factor Models
- 3. Forecasting Volume
- 4. Big Data – Advanced Analytics
- 5. FX Derivatives
- 6. Interest Rate Derivatives and Models
- 7. Exotic Options
- A general pricing approach
- The role of dynamic hedging
- How R can help a lot
- A glance beyond vanillas
- Greeks – the link back to the vanilla world
- Pricing the Double-no-touch option
- Another way to price the Double-no-touch option
- The life of a Double-no-touch option – a simulation
- Exotic options embedded in structured products
- References
- 8. Optimal Hedging
- 9. Fundamental Analysis
- 10. Technical Analysis, Neural Networks, and Logoptimal Portfolios
- 11. Asset and Liability Management
- 12. Capital Adequacy
- 13. Systemic Risks
- V. Module 5: Machine Learning with R module
- 1. Introducing Machine Learning
- 2. Managing and Understanding Data
- R data structures
- Managing data with R
- Exploring and understanding data
- Exploring the structure of data
- Exploring numeric variables
- Measuring the central tendency – mean and median
- Measuring spread – quartiles and the five-number summary
- Visualizing numeric variables – boxplots
- Visualizing numeric variables – histograms
- Understanding numeric data – uniform and normal distributions
- Measuring spread – variance and standard deviation
- Exploring categorical variables
- Exploring relationships between variables
- 3. Lazy Learning – Classification Using Nearest Neighbors
- 4. Probabilistic Learning – Classification Using Naive Bayes
- 5. Divide and Conquer – Classification Using Decision Trees and Rules
- Understanding decision trees
- Example – identifying risky bank loans using C5.0 decision trees
- Understanding classification rules
- Example – identifying poisonous mushrooms with rule learners
- 6. Forecasting Numeric Data – Regression Methods
- Understanding regression
- Example – predicting medical expenses using linear regression
- Understanding regression trees and model trees
- Example – estimating the quality of wines with regression trees and model trees
- 7. Black Box Methods – Neural Networks and Support Vector Machines
- 8. Finding Patterns – Market Basket Analysis Using Association Rules
- 9. Finding Groups of Data – Clustering with k-means
- 10. Evaluating Model Performance
- 11. Improving Model Performance
- 12. Specialized Machine Learning Topics
- Working with proprietary files and databases
- Working with online data and services
- Working with domain-specific data
- Improving the performance of R
- Managing very large datasets
- Learning faster with parallel computing
- GPU computing
- Deploying optimized learning algorithms
- Building bigger regression models with biglm
- Growing bigger and faster random forests with bigrf
- Training and evaluating models in parallel with caret
- A. Reflect and Test Yourself Answers
- Module 1: Data Analysis with R
- Chapter 1: RefresheR
- Chapter 2: The Shape of Data
- Chapter 3: Describing Relationships
- Chapter 4: Probability
- Chapter 5: Using Data to Reason About the World
- Chapter 6: Testing Hypotheses
- Chapter 7: Bayesian Methods
- Chapter 8: Predicting Continuous Variables
- Chapter 9: Predicting Categorical Variables
- Chapter 10: Sources of Data
- Chapter 11: Dealing with Messy Data
- Chapter 12: Dealing with Large Data
- Module 2: R Graphs
- Chapter 1: R Graphics
- Chapter 2: Basic Graph Functions
- Chapter 3: Beyond the Basics – Adjusting Key Parameters
- Chapter 4: Creating Scatter Plots
- Chapter 5: Creating Line Graphs and Time Series Charts
- Chapter 6: Creating Bar, Dot, and Pie Charts
- Chapter 7: Creating Histograms
- Chapter 8: Box and Whisker Plots
- Chapter 9: Creating Heat Maps and Contour Plots
- Module 4: Mastering R for Quantitative Finance
- Module 5: Machine Learning with R
- Chapter 1: Introducing Machine Learning
- Chapter 2: Managing and Understanding Data
- Chapter 3: Lazy Learning – Classification Using Nearest Neighbors
- Chapter 4: Probabilistic Learning – Classification Using Naive Bayes
- Chapter 5: Divide and Conquer – Classification Using Decision Trees and Rules
- Chapter 6: Forecasting Numeric Data – Regression Methods
- Chapter 7: Black Box Methods – Neural Networks and Support Vector Machines
- Chapter 8: Finding Patterns – Market Basket Analysis Using Association Rules
- Module 1: Data Analysis with R
- B. Bibliography
- Index
These are just four of the most popular classifiers out there, but there are many more to choose from. Although some classification mechanisms perform better on some types of datasets than others, it can be hard to develop an intuition for exactly the ones they are suitable for. In order to help with this, we will be examining the efficacy of our four classifiers on four different two-dimensional made-up datasets—each with a vastly different optimal decision boundary. In doing so, we will learn more about the characteristics of each classifier and have a better sense of the kinds of data they might be better suited for.
The four datasets are depicted in Figure 9.11:

Figure 9.11: A plot depicting the class patterns of our four illustrative and contrived datasets
The first contrived dataset we will be looking at is the one on the top-left panel of Figure 9.11. This is a relatively simple classification problem, because, just by visual inspection, you can tell that the optimal decision boundary is a vertical line. Let's see each of our classifiers fair on this data set:

Figure 9.12: A plot of the decision boundaries of our four classifiers on our first contrived dataset
As you can see, all of our classifiers performed well on this simple data set; all of the methods find an appropriate straight vertical line that is most representative of the class division. In general, logistic regression is great for linear decision boundaries. Decision trees also work well for straight decision boundaries, as long as the boundaries are orthogonal to the axes! Observe the next dataset.
The second dataset sports an optimal decision boundary that is a diagonal line—one that is not orthogonal to the axes. Here, we start to see some cool behavior from certain classifiers.

Figure 9.13: A plot of the decision boundaries of our four classifiers on our second contrived dataset
Though all four classifiers were reasonably effective in this data set's classification, we start to see each of the classifiers' personality come out. First, the k-NN creates a boundary that closely approximates the optimal one. The logistic regression, amazingly, throws a perfect linear boundary at the exact right spot.
The decision tree's boundary is curious; it is made up of perpendicular zig-zags. Though the optimal decision boundary is linear in the input space, the decision tree can't capture its essence. This is because decision trees only split on a function of one variable at a time. Thus, datasets with complex interactions may not be the best ones to attack with a decision tree.
Finally, the random forest, being composed of sufficiently varied decision trees, is able to capture the spirit of the optimal boundary.
This third dataset, depicted in the bottom-left panel of Figure 9.11, exhibits a very non-linear classification pattern:

Figure 9.14: A plot of the decision boundaries of our four classifiers on our third contrived dataset
In the preceding figure, our top performers are k-NN—which is highly effective with non-linear boundaries—and random forest—which is similarly effective. The decision tree is a little too jagged to compete at the top level. But the real loser here is logistic regression. Because logistic regression returns linear decision boundaries, it is ineffective at classifying these data.
To be fair, with a little finesse, logistic regression can handle these boundaries, too, as we'll see in the last example. However, in highly non-linear situations, where the nature of the non-linear boundary is unknown—or unknowable—logistic regression is often outperformed by other classifiers that natively handle these situations with ease.
The last dataset we will be looking at, like the previous one, contains a non-linear classification pattern.
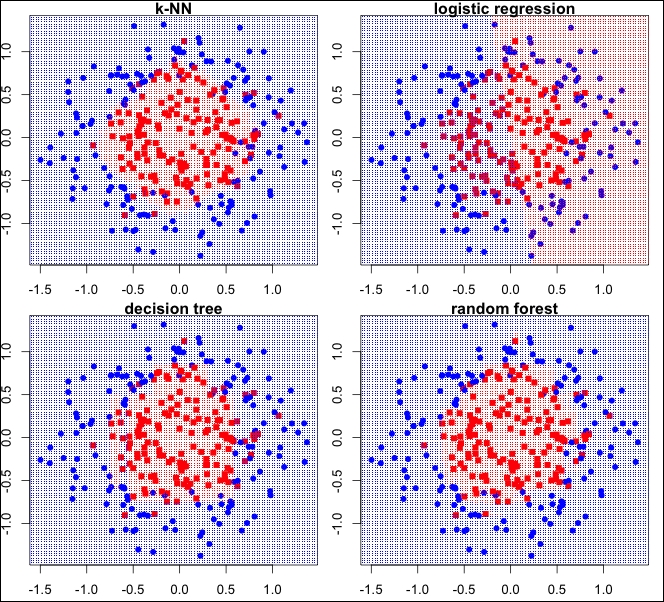
Figure 9.15: A plot of the decision boundaries of our four classifiers on our fourth contrived dataset
Again, just like in the last case, the winners are k-NN and random forest, followed by the decision tree with its jagged edges. And, again, the logistic regression unproductively throws a linear boundary at a distinctively not-linear pattern. However, stating that logistic regression is unsuitable for problems of this type is both negligent and dead wrong.
With a slight change in the incantation of the logistic regression, the whole game is changed, and logistic regression becomes the clear winner:
> model <- glm(factor(dep.var) ~ ind.var1 + + I(ind.var1^2) + ind.var2 + I(ind.var2^2), + data=this, family=binomial(logit))

Figure 9.16: A second-order (quadratic) logistic regression decision boundary
In the preceding figure, instead of modeling the binary dependent variable (dep.var) as a linear combination of solely the two independent variables (ind.var1 and ind.var2), we model it as a function of those two variables and those two variables squared. The result is still a linear combination of the inputs (before the inverse link function), but now the inputs contain non-linear transformations of the other original inputs. This general technique is called
polynomial regression and can be used to create a wide variety of non-linear boundaries. In this example, just squaring the inputs (resulting in a quadratic polynomial) outputs a classification circle that exactly matches the optimal decision boundary, as you can see in Figure 9.16. Cubing the original inputs (creating a cubic polynomial) suffices to describe the boundary in the previous example.
In fact, a logistic regression containing polynomial terms of arbitrarily large order can fit any decision boundary—no matter how non-linear and complicated. Careful, though! Using high order polynomials is a great way to make sure you overfit your data.
My general advice is to only use polynomial regression for cases where you know a priori what polynomial form your boundaries take on—like an ellipse! If you must experiment, keep a close eye on your cross-validated error rate to make sure you are not fooling yourself into thinking that you are doing the right thing taking on more and more polynomial terms.


-
No Comment