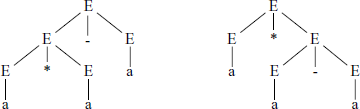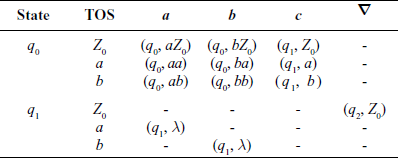A.5 Context-free Languages, CFG and Push-down Automata
Context-free Languages (CFL) have structures which cannot be specified by regular expressions. Most of the computer programming languages are of this type. The grammar which can specify a CFL is called Context-free Grammar (CFG) and acceptor for such a language is called Push-down Automata (PDA).
A.5.1 Context-free Language
We consider first an example:
Palindrome language PAL over ∑ = {a, b} can be defined as:
- λ, a, b ∈ PAL
- ∀ S ∈ PAL, aSa, bSb ∈ PAL
- no other string in PAL unless it can be obtained by applying (1) and (2).
Typical strings in PAL are: a, b, aa, bb, aaa, aba, bab, ![]() ,…
,…
We can write the corresponding grammar immediately as:
Note the occurrence of S on the RHS in rule (2), which makes it a recursive production. This is one of the characteristic features of a CFG.
A.5.2 Context-free Grammars
A CFG is a 4-tuple G =< VN , ∑, S, P >, where
VN is a finite set of variables or non-terminals;
∑ is a finite set, alphabet, of finals or Terminals; VN ∩ ∑ = Ø;
S is the starting symbol, S ∈ VN;
P is a finite set of Production Rules, of the form A → α, where A ∈ VN and α ∈ V* = (VN ∪ ∑)*.
We use the symbol ![]() for example
for example ![]() to mean “β is derivable from α” which denotes that a string (a sentential form) β can be derived from α, using a rule of grammar G.
to mean “β is derivable from α” which denotes that a string (a sentential form) β can be derived from α, using a rule of grammar G.
The closure operation ![]() means “β is derivable from a in zero or more steps”.
means “β is derivable from a in zero or more steps”.
Note the use of the three words:
String: Any arbitrary string derived from an alphabet;
Sentence: Any string strictly in a specified language, i.e. derivable from staring symbol S, containing only T symbols;
Sentential form: A string of T and NT symbols derivable from the staring symbol S.
We also use the following terms while discussing parsing theory:
Phrase: In a sentential form, σ = Ø1βØ2, β is a phrase If ![]() and
and ![]()
Simple phrase: If in the above formula, A ⇒ β, then β is a simple phrase.
Handle: Of a sentential form is, it is leftmost simple phrase.
Definition: Let G = < VN , ∑, S, P > be a CFG. The language generated by
A given language L is CFL if there is a grammar CFG G such that L = L(G).
We give here a theorem about CFL, without giving its proof.
Theorem A.5.1 (Union, catenation and closure of CFL) If L1 and L2 are CFL, then so are L1 ∪ L2, ![]()
Derivation and Ambiguity
Example: Consider a grammar for algebraic expressions, G1: VN = {E}, ∑ = {+, –, *, /, (, ), a}, S = E, and P is given by:
P = {
1. E → E + E
2. E → E – E
3. E → E * E
4. E → E/E
5. E → (E)
6. E → a
}
This is an ambiguous grammar, because there is more than one way in which a sentence can be derived, see Fig. A.13.
To remove this ambiguity, G1 can be rewritten as a non-ambiguous grammar or the ambiguity can be resolved by some other means, such as defining the precedence of the operator symbols.
A normalized or canonical derivation is used to remove even a trivial ambiguity where the resultant derivation tree is the same.
Definition A.5.1 (Leftmost derivation) A leftmost derivation is one in which, at every step of derivation from some initial NT to the final sentence, we always replace the leftmost NT in the sentential form.
We could also similarly define a rightmost derivation which is used in Bottom-up parsing.
Definition A.5.2 (Ambiguous grammar) A CFG G is ambiguous If at least one sentence in L(G) has more than one distinct leftmost derivations.
A well-known example of ambiguity is the nested if-then-else structure.
A non-ambiguous version for ![]() and P is given by:
and P is given by:
P = {
1. E → E + T | E – T | T
3. T → T * F | T/F | F
3. F → (E) | a
}
Simplification of Grammar
There are several features in a grammar which make it difficult to deal with:
λ-productions have the form A → λ. If λ ∈ L(G), we cannot remove all such productions, but can ensure that L(G) –{λ} can be generated by a λ-less grammar.
Unit productions of the form A → B or even A → A.
Useless NT and productions which are never used in production of any sentence in the language. An NT may be either unreachable – no path from S, or dead-end – no further productions.
Chomsky Normal Form
A grammar given in this form is not only simplified, but has further restrictions on the productions.
A CFG G = < VN , ∑, S, P > is in CNF if every production in P is in one of the forms A → BC, or A → a, where A, B, C ∈ VN and a ∈ ∑.
Greibach Normal Form
A grammar given in this form is useful for constructing parsers.
A CFG G = < VN , ∑, S, P > is in GNF if every production in P is of the forms A → α, where α can be represented by an RE ∑VN*, i.e. each RHS starts with a T symbol followed by zero or more NTs.
To convert a CFG to GNF, we must remove any left-recursive rules of the form A → Aα.
A.5.3 Push-down Automata
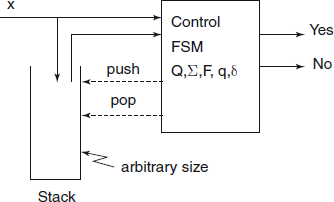
Finite-state machines are limited in ability due to their limited “memory”, which is in the form of the states of the FSM. As we have finite and fixed number of states in any particular FSM, it cannot recognize certain kinds of languages.
If we add a separate, possibly arbitrary size, memory to an FSM, then can we make the machine more powerful? The FSM would then keep track of only the overall situation and details of the input string, sentential forms, etc. be held in that memory. PDA is such a machine, with a push-down stack (a LIFO) as the memory (see Fig. A.14).
Each action of a PDA depends upon the current state of the FSM controller, the next input symbol and top-of-stack symbol (TOS). The actions are:
- Decide the next state of FSM and take a transition to that state;
- Replace the TOS with one or more symbols, including λ, which means effectively pop-off TOS.
Definition A.5.3 (PDA) A PDA is a 7-tuple, M = < Q, ∑, Γ, q0, Z0, δ, F > where
Q – set of states in FSM part;
∑ – input alphabet;
Γ – alphabet on the stack;
q0 – the starting state of FSM;
Z0 – the initial symbol on the stack;
δ – transition function: Q×∑×Γ→ Q × Γ*;
F – set of acceptance or final states of FSM.
If it is a non-deterministic PDA (NPDA), then δ: Q × ∑ × Γ → finite subsets of (Q × Γ*).
While showing the contents of the stack, it is helpful if it is shown horizontally as ![]()
Definition A.5.4 (PDA configuration) A configuration of PDA, written as (q, x, α), where q ∈ Q is the current state of FSM, x ∈ ∑* unread portion of the input and α ∈ Γ* is current stack contents.
We say that some configuration (p, ay, Xβ) derives some other configuration (q, y, γβ), written as
if δ contains the pair (q, γ).
We can extend this definition for k steps by writing ![]() and similarly,
and similarly, ![]() defines a derivation in zero or more steps.
defines a derivation in zero or more steps.
A PDA can accept a string in two ways:
Definition A.5.5 (Acceptance by final state) For a PDA defined as a 7-tuple as above, then a string x ∈ ∑ * is accepted by final state If ![]() for some α ∈ ∑* and qf ∈ F.
for some α ∈ ∑* and qf ∈ F.
Definition A.5.6 (Acceptance by empty stack) A string x ∈ ∑* is accepted by empty stack If ![]()
![]() for some q ∈ Q.
for some q ∈ Q.
The corresponding languages are denoted by Lf(M) and Le(M).
Theorem A.5.2 The two types of acceptances are equivalent, i.e. they recognize the same language.
Example
Consider the language L = {xcREV (x) | x ∈ {a, b}*}. Here, ∑ = {a, b, c, ∇},Γ= {a, b, Z0}, Q = {q0, q1, q2}, q0 is the starting state, F = {q2}. Note that symbol ∇ is used to denote end of string marker.
The transition function δ is shown in Table A.5.
For an input string “abcba”, the operation of the machine is shown Table A.6.
Theorem A.5.3 For every CFG G, there is a PDA recognizing the language L(G).
Theorem A.5.4 For every PDA M, there is a CFG G, generating a language L(G), such that M recognizes the language L(G).
A.5.4 Pumping Lemma for Context-free Languages
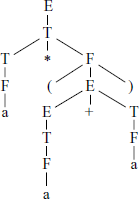
The pumping lemma for class CFL is derived from the corresponding grammar. Consider the grammar ![]() used as an example in Section A.5.2. If we derive a string “a * (a + a)” in this grammar, the derivation tree will be as shown in Fig. A.15.
used as an example in Section A.5.2. If we derive a string “a * (a + a)” in this grammar, the derivation tree will be as shown in Fig. A.15.
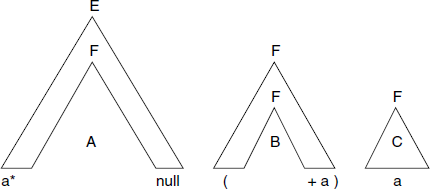
This derivation tree can be broken down into three “jig-saw pieces” as shown in Fig. A.16.
The pieces are named as A, B and C and represent portions of the given string and the NT from which that portion is derived. The label at the top of a piece shows the “socket” where the piece can be plugged-in. For example, piece B can be plugged-in at a socket labelled F. So can piece C also. Some of the ways in which we can plug the pieces is shown in Fig. A.17.
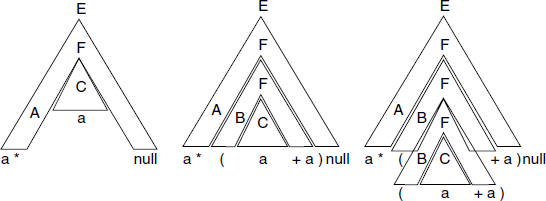
Fig. A.17 Some of the combinations of the three jig-saw pieces; first generates string a * a, second a * (a + a) and third a * ((a + a) + a)
This idea is the basis of the pumping lemma for a CFG. It will be easier if the grammar is in CNF.
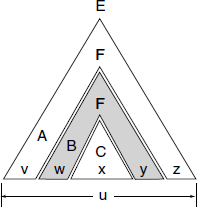
Theorem A.5.5 (Pumping Lemma – 1st form) Let G = < VN, ∑, S, P > be a CFG expressed in CNF, with a total of n NTs. If u ∈ L(G), | u | ≥ 2n+1, then u may be written as: u = vwxyz, for some v, w, x, y and z, satisfying | wy | > 0, | wxy | ≤ 2n+1 and this further implies that ∀m > 0, vwmxymz ∈ L(G).
See Fig. A.18, in which the shaded portion – piece B – can be iterated 0 or more times.
Theorem A.5.6 (Pumping Lemma – 2nd form) Here we remove the requirement that the grammar should be given as CNF. Let L be a CFL. There is an integer N such that for any u ∈ L, | u | ≥ N, there are strings v, w, x, y and z satisfying | wy | > 0, | wxy | ≤ N and further,∀ m ≤ 0, vwmxymz ∈ L.
Example
Show that the language L = {xayb | x, y ∈ {a, b}* and | x | = | y |} is CFL by using pumping lemma.
Select v = null, w = {a, b}, x = a, y = {a, b} and z = b. Then it is easy to see that the lemma is satisfied and thus L is CFL.