6
Labour
CHAPTER OUTLINE
3. Important Factors for Controlling Labour Cost
4. Distinction between Direct and Indirect Labour Costs
10. Differential Piece-Rate System (or Taylor's Plan)
11. Merrick's Multiple Piece-Rate Plan
12. Gantt's Task and Bonus Wage Plan
LEARNING OBJECTIVES
After reading this chapter, you should be able to understand the following topics:
- Important factors for controlling labour cost
- Distinction between direct and indirect labour costs
- Labour turnover
- Causes of labour turnover
- Effects of labour turnover
- Measurement of labour turnover
- Time study
- Motion study
- Piece-rate system
- Incentive system of wage payment
6.1 INTRODUCTION
The second most important element of cost (material being the first one) of production is labour. Labour refers to human contribution to production. The efficiency of production to a large extent depends on the proper utilization of labour force. Therefore, control of labour cost is a major problem before a firm's management.
6.2 LABOUR COST
Labour cost is one of the most important factors considered by an entrepreneur before venturing into the industrial field. It helps in studying the extent of expenditure incurred by entrepreneurs on labour welfare and social security aspects, in addition to wages/salaries paid to labour.
Study of labour costs also helps in fixing wages on a realistic basis, logical collective bargaining, evaluation of welfare measures, studying trends over a period of time, deciding on the location of an industry, etc. Labour cost data are also important for policy formulation at the national and regional levels.
Various aspects of labour cost, such as wages/salaries, bonuses, contributions to provident and other funds, and staff welfare expenses for all employees employed directly or through contractors, are collected every year. The total of these components gives the labour cost. When used in line with the number of man-days worked, this gives the average labour cost per man-day worked.
6.3 IMPORTANT FACTORS FOR CONTROLLING LABOUR COST
To exercise an effective control over labour costs, the essential requisite is efficient utilization of labour and allied factors. The main points that need to be considered for controlling labour costs are the following:
- Assessment of manpower requirements.
- Control over timekeeping and time booking.
- Time and motion study.
- Control over idle time and overtime.
- Control over labour turnover.
- Wage systems.
- Incentive systems.
- Systems of wage payment and incentives.
- Control over casual, contract and other workers.
- Job evaluation and merit rating.
- Labour productivity.
6.4 DISTINCTION BETWEEN DIRECT AND INDIRECT LABOUR COSTS
Any labour cost that is specifically incurred for or can be readily charged to or identified with a specific job, contract, work order or any other unit of cost is termed direct labour cost; it includes all labour that is engaged in converting raw materials into manufactured articles in the case of manufacturing industries and other forms of labour that, although not immediately engaged in converting raw materials into manufactured articles, nonetheless are incurred wholly or specifically for any particular unit of production and, hence, can be readily identified with the unit of production.
Individual incentive plan
Straight piecework plan
Standard hour plan
Bedeaux plan
Taylor's differential piece-rate system
Merrick's multiple piece-rate system
Halsey's 50–50 method
Rowan's plan
Gantt's plan
6.5 LABOUR TURNOVER
Labour turnover is the rate at which employees join and leave an organization. In other words, it refers to ‘how long employees tend to stay’ or ‘the rate of traffic through the revolving door’. Turnover is measured for individual companies and for their industry as a whole. If an organization experiences higher rate of labour turnover as compared to their competitor, it is going to affect them adversely. High turnover can be harmful to a company's productivity if skilled workers are often leaving and the worker population contains a high percentage of novice workers.
It is a normal feature in every organization that some workers leave their jobs and some new workers take their place. This change in the labour force is known as labour turnover. In other words, labour turnover denotes the percentage of change in the labour force in an organization. Labour turnover refers to the number of workers left during the period in relation to the average number of workers employed during the period. It refers to the rate of displacement of labour employed in an organization. A high rate of labour turnover denotes that labour is not stable and that there is frequent change in the labour force in an organization. A high labour turnover rate (LTR) is an important indication of high labour cost. It is therefore not desirable.
6.5.1 Internal versus external turnover
Turnover can be classified as ‘'internal'’ or ‘'external'’. Internal turnover involves employees leaving their current positions and taking up new positions within the same organization. Both positive and negative effects of internal turnover exist and, therefore, it may be equally important to monitor this form of turnover as it is to monitor its external counterpart. Internal turnover might be moderated and controlled by typical human resources (HR) mechanisms, such as an internal recruitment policy or formal succession planning.
6.5.2 Voluntary versus involuntary turnover
Experts differentiate between instances of voluntary turnover, which are initiated at the choice of an employee, and instances of involuntary turnover, where the employee has no choice in his or her termination (such as long-term sickness, death, moving overseas, or employer-initiated termination).
Models of turnover
Over the years, there have been thousands of research articles exploring the various aspects of turnover, and in due course several models of employee turnover have been promulgated. The first model, and by far the one inviting the most attention from researchers, was put forward in 1958 by March and Simon. After this model was proposed, there were several efforts to extend the concept. Since 1958 the following models of employee turnover have been published:
- March and Simon (1958)—Process Model of Turnover
- Porter and Steers (1973)—Met Expectations Model
- Price (1977)—Causal Model of Turnover
- Mobley (1977)—Intermediate Linkages Model
- Hom and Griffeth (1991)—Alternative Linkages Model of Turnover
- Whitmore (1979)—Inverse Gaussian Model for Labour Turnover
- Steers and Mowday (1981)—Turnover Model
- Sheridan & Abelson (1983)—Cusp Catastrophe Model of Employee Turnover
- Jackofsky (1984)—Integrated Process Model
- Lee et al. (1991)—Unfolding Model of Voluntary Employee Turnover
- Aquino et al. (1997)—Referent Cognitions Model
- Mitchell and Lee (2001)—Job Embeddedness Model
6.5.3 Causes of labour turnover
A minimum value of labour turnover is common and is good for all industries. But excessive or high labour turnover is dangerous. Excessive labour turnover may occur due to the following reasons:
- Avoidable causes: low wages and allowances, dissatisfaction with the job, poor working conditions, odd working hours, poor interpersonal relationships, poor welfare facilities, unfair methods of product promotion.
- Unavoidable causes: retirement, death while in service, accident, illness, dismissals and marriages in case of women.
6.5.4 Effects of labour turnover
The major effects of labour turnover are as follows:
- Increased cost of new recruitment and training
- Interruption in production
- Decrease in production
- Lack of coordination
- New workers are more prone to accidents.
6.5.5 Costs of labour turnover
The major costs of labour turnover are as follows:
- Additional recruitment costs
- Lost production costs
- Increased costs of training replacement employees
- Loss of know-how and customer goodwill
- Potential loss of sales (for example, if there is high turnover among the sales force)
- Damage that may occur to morale and productivity (an intangible cost)
6.5.6 Benefits of labour turnover
Labour turnover does not just create costs. Some level of labour turnover is important to bring in new ideas, skills and enthusiasm to the labour force. A ‘natural’ level of labour turnover can be a way in which a business can slowly reduce its workforce without having to resort to redundancies.
6.5.7 Measurement of labour turnover
There are three methods for measuring labour turnover:
- Separation method (number of employees leaving):
- Replacement method (number of employees joining):

- Flux rate method (number of separations + number of replacements):
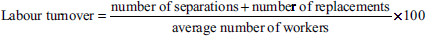
Illustration 1
From the following data provided, find the LTR by applying the (a) flux, (b) replacement and (c) separation methods:
| Number of workers on the payroll: | |
| At the beginning of the month | 450 |
| At the end of the month | 550 |
During the month, eight workers left, 25 workers were discharged and 80 workers were recruited. Of these, 10 workers were recruited in the vacancies of those leaving, whereas the rest of the workers were engaged for an expansion scheme.
Solution:
- LTR by applying the flux method:

- LTR by applying the replacement method:
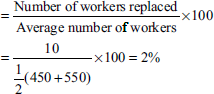
- LTR by applying the separation method:
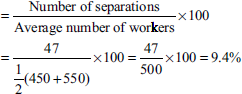
Problem 1.
From the following particulars supplied by the personnel department of a firm, calculate labour turnover:
| Total number of employees at the beginning of the month | 2,010 |
| Number of employees recruited during the month | 50 |
| Number of employees who left during the month | 100 |
| Total number of employees at the end of the month | 1,990 |
Illustration 1a
From the following information, calculate LTR:
| Number of workers at the beginning of the year | 3,900 |
| Number of workers at the end of the year | 4,300 |
During the year, 80 workers left while 160 workers were discharged. A total of 800 workers were recruited during the year; of these, 200 workers were recruited because of leavers and the rest were engaged in accordance with an expansion scheme.
Solution:
LTR:

Labour flux rate:

Labour flux rate denotes total change in the composition of labour force due to additions and separations of workers.
Problem 1a. Raghavendra Metal Company gives the following information
| Number of employees on 1 April 1989: 200 |
| Number of employees on 31 March 1990: 240 |
| Number of employees resigned: 40 |
| Number of employees discharged: 26 |
| Number of employees replaced: 11 |
Calculate labour turnover by applying the three methods.
[Madras, B.Sc., (ICE) May 2000; Bharathidasan, B.Com., April 1991]
[Ans: labour turnover under (a) separation method—18.18%, (b) replacement method—5% and (c) flux method—23.18%]
Illustration 1b
From the following data, find the LTR by applying the (a) flux, (b) replacement and (c) separation methods.
The number of workers on the payroll at the beginning of the month is 500 and that at the end of the month is 600. During the month, 15 workers left, 25 workers were discharged and 150 workers were recruited. Of these, 45 workers were recruited in the vacancies of those leaving, whereas the remaining workers were engaged for an expansion scheme.
Solution: Determination of LTR:
- Flux method
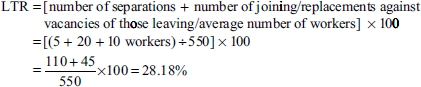
- Replacement method
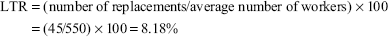
- Separation method
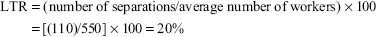
Problem 1b. The personnel department of a concern provides the following information regarding its labour
| Number of employees on 1 January: 1,800 |
| Number of employees on 31 January: 2,200 |
During the month, 20 workers quit and services of 80 workers were terminated. Three-hundred workers are needed; of these, 50 workers are recruited. Calculate LTR.
[Madras, B.Com., (ICE) May 1999]
[Ans: LTR under (a) separation method—10%, (b) replacement method—2.5% and (c) flux method—12.5%]
Hint: The number of workers needed is irrelevant. Those who are actually recruited alone should be taken into account.
Illustration 2
Different methods of labour turnover
- What is meant by the term labour turnover? What is the effect of labour turnover on cost of production?
- From the following data given by the personnel department, calculate LTR by applying the (a) separation, (b) replacement and (c) flux methods:
Number of workers on the payroll: At the beginning of the month 1,200 At the end of the month 1,500
During the month, 20 workers left, 50 workers were discharged and 200 workers were recruited. Of these, 30 workers were recruited in the vacancies of those leaving, whereas the rest were engaged for an expansion scheme.
Solution:
Average number of workers = (1,200 + 1,500) ÷ 2 = 1,350
- Separation method

- Replacement method

- Flux method
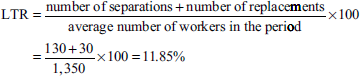
Problem 2. From the following data provided, find the LTR by applying the (a) flux, (b) replacement and (c) separation methods
| Number of workers on the payroll: | |
| At the beginning of the month | 500 |
| At the end of the month | 600 |
During the month, five workers left, 20 workers were discharged and 125 workers were recruited. Of these, 10 workers were recruited in the vacancies of those leaving, whereas the rest were engaged for an expansion scheme.
[I.C.W.A. Inter, June 1993]
[Ans: (a) 18.18%, (b) 1.82%, (c) 20%]
Hint: Replacement method ignores recruitment for expansion. Flux method includes all recruitments including those for expansion.
Illustration 2a
The number of workers on the roll at the commencement of the year were 9,000 and at the end of the year 8,000. The number of separations and replacements during the year were 2,000 and 1,500, respectively. Calculate LTR with the help of the flux method.
Solution: Labour turnover under the flux method:
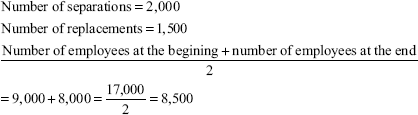
∴ Under the flux method, LTR is calculated as follows:
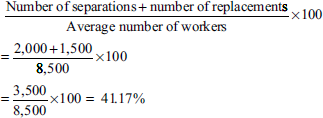
Problem 2a. The following information is extracted from the records of a company for the month of October 1998:
| Number of employees at the beginning of the month | 950 |
| Number of employees at the end of the month | 1,050 |
| Number of employees who resigned | 10 |
| Number of employees who were discharged | 30 |
| Number of employees replaced in the vacancies | 20 |
| Number of employees appointed due to an expansion scheme | 120 |
Calculate LTR.
[Madras, B.Com., C & M, Oct. 1990]
[Ans: LTR under (a) separation method—4%, b) replacement method—2%; and (c) flux method—18%]
Hint: Replacement method ignores recruitment for expansion, and flux method includes all recruitments including those for expansions.
6.6 TIME AND MOTION STUDY
It is the analysis of time spent in going through the different motions of a job. Such studies were first instituted in offices and factories in the United States in the early twentieth century. They were widely adopted as a means of improving work methods by subdividing the different operations of a job into measurable elements.
The first effort at time study was made by F. W. Taylor in the 1880s. Early in the twentieth century, Frank and Lillian Gilbreth developed a more systematic and sophisticated method of time and motion study for industry, taking into account the limits of human physical and mental capacity and the importance of a good physical environment.
The idea of a time and motion study is even today often associated with production lines and the manufacturing industry. It is understood as a source of disagreement between management and workers. However, if used properly a time and motion study can be of benefit to modern companies and their workforce. Unfortunately, too many companies still see a time and motion study as simply a way to increase profits with no benefits returning to the workforce who are ultimately responsible for those profits.
6.6.1 Time study
Time study is an art of observing and recording the time required to complete a job. This analysis involves consideration of the following points:
- The worker should have average efficiency.
- The standard fixed cost may change from industry to industry.
- The person who observes the time (timekeeper) must be very careful.
- The standard cost should include necessary rest and accidental and unavoidable delays.
The time study finds the differences between efficient and inefficient workers.
6.6.2 Motion study
Motion study is an art of observing and recording the movements required to complete a job. There are 17 fundamental motions, which are always present in every human activity. Such studies help in eliminating the unnecessary movements of workers and avoid the wastage of energy.
The standard time can be determined accurately with the help of time and motion studies, which is important for determining labour remuneration.
6.6.3 Merits of time and motion studies
The following are some important advantages of time and motion studies:
- These studies help in determining the proper speed of work by eliminating unnecessary movements.
- They help in the fixation of suitable wage rates and introduction of wage incentive plans.
- Efficiency of workers is increased because they are asked to follow correct procedures and methods of work by avoiding useless movements and to save time and energy.
- They help in increasing output, result in greater efficiency in plant organization and lessen human fatigue.
- They help in assessing the correct labour requirements of an organization.
- These studies help to reduce cost of production per unit and increase total earnings of workers.
- They facilitate labour cost budgeting and labour cost control.
6.7 TIME WAGE SYSTEM
This is the traditional method of wage payment. The time spent on work is made the basis for wage calculations. Wages are paid according to the time spent by workers irrespective of their output.
6.7.1 Merits of time wage system
The merits of the time wage system are as follows:
- Simplicity: The method of wage payment is very simple. Workers do not find any difficulty in calculating their wages in this system.
- Guaranteed wage: Workers are guaranteed minimum wages for the time spent by them on the job. There is no link between wages and output; wages are paid irrespective of output.
- Better quality: When workers are assured of wages on time basis, they tend to improve the quality of goods. If wages are related to output, then workers may think of increasing production without bothering about the quality of goods produced.
- Accepted by unions: This method is acceptable to trade unions because it does not distinguish between workers on the basis of their performance.
- Suitable for beginners: Wage rate system is good for beginners because they may not be able to reach a particular level of production in the beginning.
- Less wastage: Under this system, workers are not in a hurry to push through production. Thus, material and equipment are properly handled without wastage.
6.7.2 Demerits of time wage payment
The demerits of time wage payment are as follows:
- Absence of incentive for efficiency: This method does not distinguish between efficient and inefficient workers.
- Wastage of time: Workers may while away their time because they will not be following a target of production.
- Low production: Since wages are not related to output, workers may produce goods at a slower rate.
- Difficulty in determining labour cost: Because wages are not related to output, employees find it difficult to determine labour cost per unit.
- Need for more supervision: Under this system, workers are not offered incentives for production.
- Employer–employee trouble: Treating all employees equally might lead to trouble between the management and workers.
6.8 PIECE WAGE SYSTEM
Piecework or piece work describes the types of employment in which a worker is paid a fixed ‘piece rate’ for each unit produced or action performed. Piecework is also a form of performance-related pay (PRP) and is the oldest form of performance pay.
In a manufacturing setting, the output of piecework can be measured by the number of physical items (pieces) produced, such as when a garment worker is paid per operational step completed regardless of the time required for the step. In a service setting, the output of piecework can be measured by the number of operations completed, as when a telemarketer is paid by the number of calls made or completed regardless of the outcome of the calls (pay for only certain positive outcomes is more likely to be called a sales commission or incentive pay).
6.8.1 Advantages of the piece wage system
- Piece rate can be used for jobs in which the quantity of work done by a person can be measured.
- Piece rate can be modified to provide a guaranteed hourly or weekly minimum wage.
- Piece rate can be used for jobs in which the quantity of work done by a person or a group is readily counted or calculated.
- The steadiness of production and the quality of the product are also fully ensured.
- This system encourages employees to produce more as their wages are related to their productivity.
- It is fair to both employers and employees.
- It provides workers with the opportunity to secure increased compensation.
- The computation of labour cost becomes a very easy task.
- It helps in preparing estimates or tenders.
- It is advantageous to consumers also as now they get products at affordable rates.
- Meritorious workers are rewarded and poor workers penalized under this system.
- Under this system, strict supervision of workers is not required.
6.8.2 Disadvantages of the piece wage system
The disadvantages of the piece wage system are as follows:
- It makes the workers feel insecure because they get wages on the basis of output.
- It lays too much stress on quantity of production at the cost of quality of a product.
- Labour unions oppose the system because it promotes rivalries among workers.
- This system weakens the labour unions because workers get no time for union activities.
- With the intension to produce more workers handle materials and machinery carelessly and damage them.
- In their eagerness for increased earnings, workers may exert themselves to the point of undermining their health and efficiency.
- As this system believes in strict supervision, workers turn hostile in their attitude.
6.9 STRAIGHT PIECE-RATE SYSTEM
Wages are paid in this system in accordance with the output of production. Wage is calculated irrespective of the time spent on a job. Table 6.1 shows the advantages and disadvantages of the straight piece-rate system.
Table 6.1 Advantages and Disadvantages of Straight Piece-Rate Syste
| Advantages | Disadvantages |
|---|---|
| Simple | Discourages quality focus |
| Easy-to-understand focus on productivity | No job security |
| No compensation for breakdown | |
| Suitable for efficient workers | No compensation for sickness |
| No guarantee of minimum wages | |
| Easy to pacify workers | Discourages group effort |
Suitability
|
6.10 DIFFERENTIAL PIECE-RATE SYSTEM (OR TAYLOR'S PLAN)
There are two types of wages fixes: lower and higher. Those who fail to reach the fixed standard are paid lower wages, and those who reach the standard or above the standard are given higher wages. Here the penalty for not reaching the standard is high; hence, workers tend to produce at the minimum fixed rate.
The idea behind this scheme is to induce all workers to at least attain the standard, at the same time if a worker is found efficient he or she stands to gain.
6.10.1 Advantages of the differential piece-rate system
Advantages of the differential piece-rate system are as follows:
- Provides incentives to efficient workers
- Penalizes inefficient workers
- Focuses on high production rate
- Simple and easy to implement
6.10.2 Disadvantages of the differential piece-rate system
Disadvantages of the differential piece-rate system are as follows:
- Minimum wage is not assured.
- There is no consideration for things that are beyond the control of workers, for example, machine failure and power failure.
- There is overemphasis on high production rate.
- There are chances that quality of work may suffer.
6.11 MERRICK'S MULTIPLE PIECE-RATE PLAN
This is a modification over Taylor's plan. In this plan, a minimum base wage is not guaranteed. Wage is calculated as follows:
- When output is less than 83% of standard output, the scheme for wage fixation is equal to piece-rate scheme.
- When output is 83% or more but less than 100% of the standard = 110% of piece rate.
- When output is 100% or more than 100% of the standard = 120% of piece rate.
6.11.1 Advantages of Merrick's multiple piece-rate plan
The advantage of Merrick's plan is that efficient workers are rewarded.
6.11.2 Disadvantages of Merrick's multiple piece-rate plan
The disadvantages of Merrick's plan are as follows:
- There is a wide gap between efficient and inefficient workers.
- Overemphasis is given on production.
6.12 GANTT'S TASK AND BONUS WAGE PLAN
In this plan, a minimum wage is guaranteed. Minimum wage is given to those workers who complete a job in standard time. If the job is completed in less time, then there is a hike in wage rate. This hike varies from 25% to 50% of the standard rate.
6.12.1 Advantages of Gantt's plan
The advantages of the Gantt's plan are as follows:
- Minimum wage is guaranteed.
- The plan is suited to efficient workers.
6.12.2 Disadvantages of Gantt's plan
The disadvantage of the Gantt's plan is that there is emphasis on high speed or high production rate.
6.13 HALSEY'S PREMIUM PLAN
In this plan, incentive is given to a worker who completes work before the standard time to complete a job. However, a minimum base wage is guaranteed to a worker who completes a job in the standard time fixed for the job.
6.13.1 Advantages of Halsey's premium plan
Advantages of Halsey's plan are as follows:
- It is simple.
- It benefits efficient workers.
- It causes no harm to non-performers.
- The management also benefits from the achievements of workers.
- Minimum base wage is guaranteed.
6.13.2 Disadvantages of Halsey's premium plan
Disadvantages of Halsey's plan are as follows:
- Workers get only a percentage of return on their overachievement.
- As a result of placing undue importance on quantity, quality suffers.
- Management gets the wrong picture of a worker's ability.
6.14 ROWAN'S PLAN
In this plan, an incentive for completing a job in lesser time than the standard time is paid to a worker. The incentive is paid on the basis of a ration, which is time saved over standard time per unit standard time.
6.14.1 Advantages of Rowan's plan
Advantages of the plan are as follows:
- Checks overspeeding and overstraining by workers.
- Assures minimum basic wage.
- Rewards efficiency.
6.14.2 Disadvantages of Rowan's plan
Disadvantages of the plan are as follows:
- Discourages workers from overachieving.
- Difficulty in ascertaining wages as it requires much processing of data.
- Sharing of profit for performance by workers may not be liked by them.
6.15 EMERSON'S EFFICIENCY PLAN
In this plan, a minimum time wage is guaranteed. Working conditions and standard output are fixed on the basis of time study. Bonus scheme is as follows (SO refers to standard output and GW refers to guaranteed wages):
- From 66.67% to 80% of (SO) = (GW) + 4% of output.
- From 66.67% to 90% of (SO) = (GW) + 10% of output.
- From 80% to 90% of (SO) = (GW) + 10% of output.
- From 90% to 100% of (SO) = (GW) + 20% of output.
- Above 100% of (SO) = (GW) + 20% of (SO) + 10% of the aforementioned output (SO).
6.15.1 Advantages of Emerson's efficiency plan
Advantages of Emerson's plan are as follows:
- Guarantees minimum wage till 66.67% of standard output.
- Efficient workers are rewarded handsomely.
6.15.2 Disadvantages of Emerson's efficiency plan
Disadvantages of the plan are as follows:
- Disproportionate rate of bonus below standard output
- Chances of overspeeding and compromise of quality
Illustration 3
A work measurement study was carried out in a firm for 10 hours and the following information was generated:
| Units produced | 400 | |
| Idle time | 20% | |
| Performance rating | 120% | |
| Allowance time | 10% of standard time | |
| What is the standard time for the task? |
Solution:
| Units produced | 400 | |
| Time spent | 10 hours | |
| Idle time | 20% |
Therefore, observed time per unit in minutes =
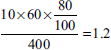
Time per unit is 1.2 minute when performance rating is 120%. Therefore, normal time per unit at 100% performance rating is
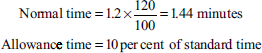
Therefore,
Alternatively, standard time may be calculated as follows:
Illustration 4
Calculate the earnings of workers A and B under straight piece-rate system and Taylor's differential piece-rate system from the following particulars
| Normal rate per hour = Rs 1.80 |
| Standard time per unit = 20 seconds |
| Differentials to be applied: |
| 80% of piece rate below standard |
| 120% of piece rate at or above standard |
| Worker A produces 1,700 units per day and worker B produces 2,000 units per day |
Solution:

Earnings of worker A:
Under straight piece-rate system,
Under Taylor's differential piece-rate system,
High piece rate has been applied because worker A's daily production of 1,700 units is more than the standard daily production of 1,440 units.
Earnings of worker B:
Under straight piece-rate system,
Under Taylor's differential piece-rate system,
High piece rate has been applied because worker B's daily production of 2,000 units is more than the standard daily production of 1,440 units.
Problem 4. On the basis of the following information, calculate the earnings of A and B under (a) straight piece-rate basis and (b) Taylor's differential rate system:
| Standard production: 8 units per hour |
| Normal time rate: Rs 4 per hour |
| Differential rates to be applied: |
| 80% of piece rate below standard |
| 120% of piece rate at or above standard |
| In a 9-hour day, A produced 54 units and B produced 75 units |
[B. Com., Andhra]
[Ans: (a) A = Rs 27.00 and B = Rs 37.50; (b) A = Rs 21.60 and B = Rs 45.00]
Illustration 5
Calculate the earnings of workers A, B and C under straight piece-rate system and Merrick's multiple piece-rate system from the following particulars:
| Normal rate per hour | Rs 1.80 |
| Standard time per unit | 1 minute |
| Output per day is as follows: | |
| Worker A: 390 units | |
| Worker B: 470 units | |
| Worker C: 575 units | |
| Working hours per day are eight. |
Solution:
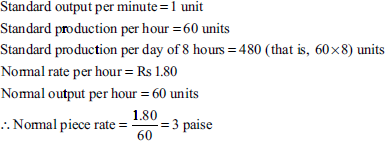
Calculation of level of performance:

Earnings of worker A:
Under the straight piece-rate system,
Under Merrick's multiple piece-rate system,
Normal piece rate has been applied because worker A's level of performance is 80%, which is below 83%.
Earnings of worker B:
Under the straight piece-rate system,
Under Merrick's multiple piece-rate system,
Worker B's level of performance is 93.75%, which is between 83% and 100%; so B is entitled to 110% of normal piece rate (that is, 110% of 3 paise or 3.3 paise per unit).
Earnings of worker C:
Under the straight piece-rate system,
Under Merrick's multiple piece-rate system,
Worker C's level of performance is 115%, which is more than 100% of standard output; so, C is entitled to 120% of normal piece rate (that is, 120% of 3 paise or 3.6 paise per unit).
Problem 5. On the basis of the following information, calculate the earnings of A, B, C and D under Merrick's differential piece-rate system
| Standard production per hour: 12 units | |
| Normal rate per unit: Rs 6 | |
| In an 8-hour day: | |
| A produced | 64 units |
| B produced | 96 units |
| C produced | 84 units |
| D produced | 100 units |
[B. Com. Tirupathi]
[Ans: A—Rs 384.00, B—Rs 633.60, C—Rs 554.40, D—Rs 720.00]
Illustration 6
From the following data, calculate the total monthly remuneration of three workers A, B and C under the Gantt's task and bonus scheme:
- Standard production per month per worker is 1,000 units
- Actual production during the month: A—950 units, B—1,050 units and C—1,150 units
- Piecework rate: 50 paise per unit
Solution: Standard production per month is 1,000 units and piecework rate is 50 paise per unit, so guaranteed monthly payment is Rs 500 (that is, 1,000 units at 50 paise).
Level of performance:

Earnings of worker A:
Worker A's level of performance is 95%, which is below the standard performance; so A will get Rs 500, which is the guaranteed monthly payment.
Earnings of worker B:
Worker B's level of performance is 105%; so B will get wages for the standard time and a 20% bonus. Thus, B's earnings will be as follows:
| Rs | |
|---|---|
| Wages for 1,000 units at 50 paise per unit | 500 |
| Add: 20% bonus | 100 |
| 600 |
Earnings of worker C:
Worker C's level of performance is 110%, which is more than the standard performance; so C will get piece wages plus 20% bonus.
Thus, his earnings are as follows:

Problem 6. The following are particulars applicable to a work process:
| Time rate: Rs 5 per hour |
| High task: 40 units per week |
| Piece rate above high task: Rs 6.50 per unit |
| In a 40-hour week, each of the following workers produced |
| A—35 units |
| B—40 units |
| C—41 units |
Calculate the wages of the workers under Gantt's task and bonus plan.
[Madras, B.A. Corp. C& M, Sept. 1990]
[Ans: earnings: A: time wages 40 × 5 = Rs 200; B: time wages + 20%, bonus = 200 + 40 = Rs 240; C: high piece rate = 41 × 6.5 = Rs 266.5]
Illustration 7
| Rate per hour = Rs 1.50 |
| Time allowed for the job = 22 hours |
| Time taken = 18 hours |
Calculate the total earnings of a worker under the Halsey plan. Also find the effective rate of earning.
Solution:

Therefore, effective rate of earning per hour
Note: The percentage of bonus is to be taken as 50% when it is not given.
Problem 7. Using the following data, calculate the wage payable to a worker under Rowan's premium bonus plan and Halsey's premium bonus plan:
| Time allowed: 40 hours |
| Time taken: 32 hours |
| Rate per hour: Rs 5.00 |
[B. Com., Nagarjuna]
[Ans: Rs 192.00 (Rowan); Rs 180.00 (Halsey)]
Illustration 8
A worker completes a job in a certain number of hours. The standard time allowed for the job is 10 hours, and the hourly rate of wages is Re 1. The worker earns at the 50% rate a bonus of Rs 3 under the Halsey plan. Ascertain the worker's total wages under the Rowan premium plan.
Solution: The worker earns Rs 3 as a bonus at 50%; so total bonus at 100% should be Rs 6. The hourly rate of wages being Re 1, the time saved should be 4 hours.
| Standard time allowed | 10 hours | |
| Add: | Time saved | 4 hours |
| Time taken | 6 hours |
Earnings under the Rowan's premium plan:
where,
T = time taken, that is, 6 hours
S = standard time, that is, 10 hours
R = rate per hour, that is, Re 1

Problem 8. In a manufacturing concern, employees are paid incentive bonus in addition to their normal wages at hourly rates. Incentive bonus is calculated in the proportion of time saved to time allowed. The following are the details of employee X
| Normal wages (rupees per hour) | 4 | |
| Completed units of production | 6,000 | |
| Time allowed (per 100 units) | 0.8 hour | |
| Actual time taken | 42 hours |
You are required to work out the amount of bonus earned and the total amount of wages received.
[Madras, B.A. Corp. C & M, March 1997]
[Ans: bonus earned = Rs 21; standard time = 48 hours; total wages = Rs 189]
Illustration 8a
From the following particulars, you are required to work out the earnings of a worker for a week under (a) straight piece-rate system, (b) differential piece-rate system, (c) Halsey's premium scheme (50% sharing) and (d) Rowan's premium scheme:
| Weekly working hours | 45 | |
| Hourly wage rate | Rs 8.00 | |
| Piece rate per unit | Rs 3.50 | |
| Normal time taken per piece | 20 minutes | |
| Normal output per week | 120 pieces | |
| Actual output per week | 150 pieces | |
| Differential piece rate | 80% of piece rate when output is below normal and 120% of piece rate when output is above normal. |
Solution: Statement showing the computation of earnings of a worker (in a week) under various wage schemes/incentives plans
| Particulars | Amount (Rs) |
|---|---|
| (a) Straight piece rate (actual output per week × piece rate per unit) = (150 units × Rs 3.5) | 525 |
| (b) Differential piece rate (actual output per week × differential piece rate per unit) = (150 units × Rs 3.5 × 120/100, as the output is above normal) | 630 |
| (c) Halsey premium scheme (hours worked per week × rate per hour) + (50% time saved in hours × hourly wage rate) = (45 hours × Rs 8) + 50% (time allowed 20/60 × 150 units = 50 hours − time taken 40 hours) × Rs 8 [= Rs 360 + Rs 40] | 400 |
| (d) Rowan premium scheme (hours worked × rate per hour) + (time saved/time allowed) × time taken × rate per hour = 45 × Rs 8 + [(10 hours/50 hours) × 40 hours × Rs 8] [= Rs 360 + Rs 64] | 424 |
Illustration 8b
Three workers (Govind, Ram and Shyam), having worked for 8 hours, produced 90, 120 and 140 pieces of a product X on a particular day in May in a factory. The time allowed for producing 10 units of X is 1 hour and their hourly rate is Rs 4. Calculate for each of the three workers earnings for the day under the (a) straight piece-rate, (b) Halsey’ premium bonus (50% sharing) and (c) Rowan's premium bonus methods of labour remuneration.
Solution:
- Straight piece-rate system:
Standard labour cost per unit (Rs.4/10) = Re 0.40
Earnings (total) = number of units produced rate per unit
Govind = (90 × Re 0.40) = Rs 36
Ram = (120 × Re 0.40 = Rs 48
Shyam = (140 × Re 0.40) = Rs 56
- Halsey's plan:
Hours worked × rate per hour) + time saved in hours × rate per hour)
Govind = (8 × Rs 4) + (0.50 × nil × Rs 4) Rs 32
Ram = (8 × Rs 4) + [0.50 × (10 – 8)] × Rs 4 = Rs 36
Shyam = (8 × Rs 4) + [0.50] × (12 – 8) × Rs 4 = Rs 40
- Rowan's plan:
(Hours worked × rate per hour) + (time saved / time allowed × time taken × rate per hour
Govind = (8 × Rs 4) + (1/8 hours) × 8 hours × Rs 4 = Rs 36
Ram = (8 × Rs 4) + (4/10) × 8 hours × Rs 4 = Rs 44.8
Shyam = (8 × Rs 4) + (6/12) × 8 hours × Rs 4 = Rs 48
Illustration 9
Standard output per day of 8 hours is 20 units. Actual output of a worker for 8 hours is 22 units. Rate per hour is Rs 2.50. Calculate the wages payable to the worker according to Emerson's efficiency plan.
Solution:
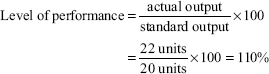
Bonus payable is 45%, which is calculated as follows:
| At 100% efficiency | 20% of time wages |
| For next 10% efficiency at 1% for each | |
| 1% increase in efficiency beyond 100% | 10% of time wages |
| Total bonus payable | 30% of time wages |
Calculation of total wages:

Problem 9. In a manufacturing concern, the daily wages guaranteed for workers is Rs 40. The standard output for a month is 1,000 articles, representing 100% efficiency. The rate of wages is paid without bonus to those workers who show up to 66 2/3% efficiency. Beyond this, bonus is payable in a graded scale
| Efficiency (%) | Bonus (%) |
|---|---|
| 90 | 10 |
| 100 | 20 |
A further increase of 1% of bonus is provided for every 1% increase in efficiency. Calculate the total earnings of A, B, C and D who have worked 26 days in a month with the following productivity: A—500 units, B—900 units, C—1,000 units and D—1,200 units.
[Mysore, B.Com.]
[Ans: earnings of workers: A (only time wages)—26 × 40 = Rs 1,040; B—1,040 + 10% of 1,040 = Rs 1,144; C—1,040 + 20% of 1,040 = Rs 1,248; D—1,040 + 40% of 1,040 = Rs 1,456]
Illustration 10
Form the following particulars prepare labour cost per man-day of 8 hours
| (a) Basic salary | Rs 4 per day |
| (b) Dearness allowance (DA) | 25 paise per every point over 100 (cost of living index for working class); current cost of living index is 800 points |
| (c) Leave salary | 10% of (a) and (b) |
| (d) Employer's contribution to provident fund (PF) | 8% of (a), (b) and (c) |
| (e) Employer's contribution to state insurance | 2.5% of (a), (b) and (c) |
| (f) Expenditure on amenities to labour | Rs 20 per head per mensem |
| (g) Number of working days in a month | 25 days of 8 hours each |
Solution: Statement of labour cost (per man-day of 8 hours):

Problem 10. From the following data, prepare a statement showing the cost per day of 8 hours of engaging a particular type of labour
| (a) | Monthly basic salary plus DA: Rs 1,200 |
| (b) | Leave salary: 5% of (a) |
| (c) | Employer's contribution to PF: 8% of (a) and (b) |
| (d) | Employer's contribution to employees’ state insurance (ESI): 2.5% of (a) and (b) |
| (e) | Pro rata expenditure on amenities to labour: Rs 100 per month |
| (f) | Number of working hours in a month: 200. |
[BCom., Madurai, Calicut]
[Ans: Rs 59.70 per day]
Illustration 11
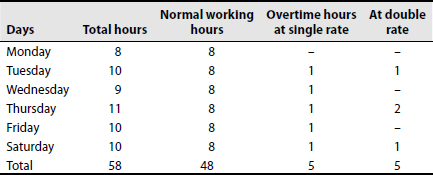
Calculate the normal and overtime wages payable to a worker from the following data:
| Days | Hours worked |
|---|---|
| Monday | 8 hours |
| Tuesday | 10 hours |
| Wednesday | 9 hours |
| Thursday | 11 hours |
| Friday | 10 hours |
| Saturday | 10 hours |
| Total | 58 hours |
| Normal working hours | 8 hours per day |
| Normal rate | Re 1 per hour |
| Overtime rate | Up to 9 hours in a day at single rate and over 9 hours in a day at double rate, or up to 48 hours in a week at single rate and over 48 hours at double rate, whichever is more beneficial to the workers |
Solution:
| Rs | |
|---|---|
| Normal wages for 48 hours at Re 1 | Rs 48 |
| Overtime wages: | |
| At single rate for 5 hours at Re 1 | Rs 5 |
| At double rate for 5 hours at Rs 2 = Rs 10 | Rs 15 |
| Total wages = | Rs 63 |
| Or | |
| Normal wages for 53 hours at Re 1 per hour = | Rs 53 |
| Overtime wages for 5 hours at Rs 2 per hour = | Rs 10 |
| Total wages = | Rs 63 |
Therefore, whichever method is followed, the amount of the wages payable to the worker is Rs 63.
Problem 11. From the following data, prepare a statement showing the cost per man-day of 8 hours:
| (a) | Basic salary and DAs: Rs 300 per month |
| (b) | Leave salary to a worker: 6% of the basic salary and DA |
| (c) | Employer's contribution to PF: 6% of (a) plus (b) |
| (d) | Employee's contribution |
| (e) | Pro rata expenditure on amenities to labour: Rs 25 per head per month |
| (f) | Number of working hours in a month: 200 |
[Madras, B.A. Corp., C & M, Sept. 1995]
[Ans: cost per man-day of 8 hours: Rs 14.48]
Hint: Ignore employee's contribution to PF.
Illustration 12
From the following particulars, prepare a statement of labour cost showing the cost per day (8 hours):
- Monthly salary: Rs 5,000
- Leave salary: 5% of basic salary
- Employer's contribution to PF: 8.5% of (a) and (b)
- Employer's contribution to ESI: 3% of (a) and (b)
- Pro rata experience on amenities to labour: Rs 600 per head per month
- Number of working hours in a month of 25 days: 8 hours per day
Solution: Statement showing the determination of labour cost per day
| Particulars | Amount (Rs) |
|---|---|
| (i) Monthly salary | 5,000 |
| (ii) Leave salary (0.05 × Rs 5,000) | 250 |
| (iii) Contribution to PF [0.85 × (Rs 5,000 + Rs 250)] | 446.25 |
| (iv) ESI (0.03 × Rs 5,250) | 157.3 |
| (v) Allocated share of expenditure on amenities | 600.0 |
| Total labour cost per month | 6,453.55 |
| Number of working days per month | 25 |
| Labour cost per day (Rs 5,828.38/25) | 258.14 |
Problem 12. From the following data, prepare a statement showing the cost per day of 8 hours of engaging in a particular type of labour:
| (a) | Monthly basic salary plus DA: Rs 400 |
| (b) | Leave salary: 5% of (a) |
| (c) | Employer's contribution to PF: 8% of (a) and (b) |
| (d) | Employer's contribution to ESI: 2 ½% of (a) and (b) |
| (e) | Pro rata expenditure on amenities to labour: Rs 35 per head per month |
| (f) | Number of working hours in a month: 200 |
[Madras, B.A. Corp., C & M, May 96]
[Ans: cost per day of 8 hours: Rs 19.96]
Illustration 13
Calculate the normal and overtime wages payable to a worker form the following data:
| Days | Hours worked |
|---|---|
| Monday | 8 |
| Tuesday | 10 |
| Wednesday | 9 |
| Thursday | 11 |
| Friday | 10 |
| Saturday | 10 |
Normal working hours are 8 hours per day, and normal rate is Rs 5 per hour. Overtime rate is up to 9 hours in a day at single rate and over 9 hours at double rate, or up to 48 hours (in a 6-day week) at single rate and over 48 hours at double rate, whichever is beneficial to the workers.
Solution: Statement showing wages payable to a worker (first method):
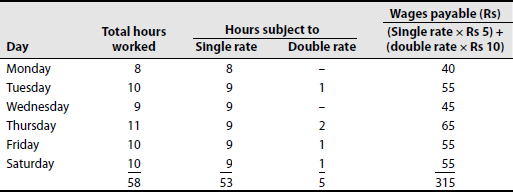
Statement showing wages payable to a worker (second method):
| (53 hours × Rs 5 per hour) | Rs 265 |
| (5 hours × Rs 10 per hour) | Rs 50 |
| Rs 315 |
Note: Both the methods yield identical sum of wages payable to a worker.
Problem 13. Calculate the normal and overtime wages payable to a worker from the following data:
| Days | Hours worked |
|---|---|
| Monday | 8 |
| Tuesday | 10 |
| Wednesday | 9 |
| Thursday | 11 |
| Friday | 9 |
| Saturday | 4 |
| Total | 51 |
Normal working hours is eight per day, and normal rate is Re 0.50 per hour. Overtime rate is up to 9 hours in a day at single rate and over 9 hours in a day at double rate, or up to 48 hours in a week at single rate and over 48 hours at double rate, whichever is more beneficial to the workers.
[Madras, B. Com., April 2001; Oct. 2000; Madras, B.Com., (ICE) May 2000 (old); Madras, B.Com. C & M, April 1998; B.Com., Sept. 1992; March 1991]
[Ans: total wages paid for the week = Rs 27; on a day basis: normal wages = Rs 22 (44 × 0.5), overtime wages = Rs 5 (4 × .5 + 3 × 1); on a weekly basis: normal wages = Rs 24 (48 × 0.5), overtime wages: Rs 3 (3 × 1)]
Hint: Saturday should be taken as half day with four normal working hours.
Illustration 14
Computation of wages under various methods of wage payment: In an engineering factory, wages are paid on a weekly basis (48 hours per week) at a guaranteed hourly rate of Rs 4.00. A study revealed that the time required to manufacture a product is 16 minutes. However, a contingency allowance of 25% is to be added to this for normal idle time, setting up time, etc. During the first week of June 1986, X produced 230 pieces. Compute X's wages for the particular week using the following methods of wage payment: (a) time rate, (b) piece rate with a guaranteed time rate, (c) Rowan's premium bonus scheme and (d) Halsey's premium bonus scheme.
Solution:
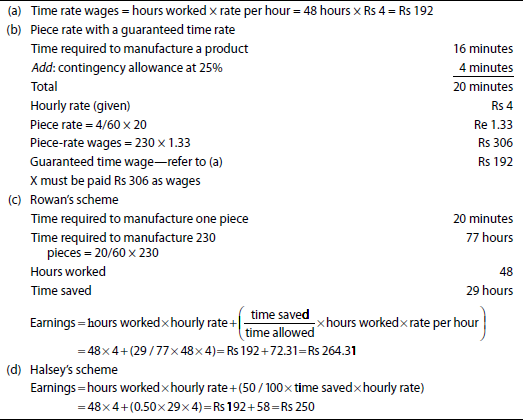
Problem 14. Compute the earnings of a worker under the (a) time rate method, (b) piece-rate method, (c) Halsey's plan and (d) Rowan's plan for the information given as follows
| Wage rate: Rs 5 per hour |
| DA: Re 1 per hour |
| Standard hours: 80 |
| Actual hours: 50 |
[B. Com., Poona]
[Ans: (a) Rs 300, (b) Rs 450, (c) Rs 375 and (d) Rs 393.75]
Illustration 15
Calculation of workers’ earnings and their allocation to jobs: Calculate the earnings of A and B from the following particulars for a month and allocate the labour cost to each job X, Y and Z:
| A | B | |
|---|---|---|
| (i) Basic wages | Rs 200 | Rs 300 |
| (ii) DA | 50% | 50% |
| (iii) Contribution to PF (on basic wages) | 8% | 8% |
| (iv) Contribution to ESI (on basic wages) | 2% | 2% |
| (v) Overtime (hours) | 12 |
The normal working hours for the month are 200. Overtime is paid at double the total of normal wages and DA. Employer's contributions to ESI and PF are at equal rates with employees’ contributions. The two workers were employed on jobs X, Y and Z in the following proportions:

Overtime was done on job Y.
Solution: Statement showing the earnings of workers A and B
| A | B | |
|---|---|---|
| Workers | Rs 200.00 | Rs 300.00 |
| Basic Wages | 100.00 | 150.00 |
| DA (50% of basic wages) | ||
| Overtime wages [2 (basic wage + DA) 12 hours] ÷ 300 | 24.00 | – |
| = (2 × 150 × 10) ÷ 200 | ___________ | ___________ |
| Gross wages earned | 324.00 | 450.00 |
| Less: PF 8% of basic wages | 16.00 | 24.00 |
| ESI: 2% | 4.00 | 6.00 |
| Wages paid (net) | 344.00 | 480.00 |
Statement of labour cost:
| Gross wages (excluding overtime; Rs) | 300 | 450 |
| Employer's contribution to PF and ESI (Rs) | 20 | 30 |
| Ordinary wages (Rs) | 320 | 480 |
| Labour rate per hour of A (320 ÷ 200) | 1.6 | |
| Labour rate per hour of B (480 ÷ 200) | 2.4 |
Statement showing allocation of wages to jobs:
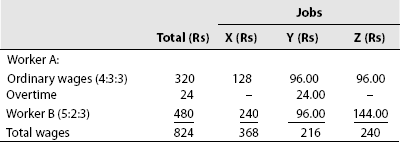
Problem 15. From the following particulars, prepare a statement of labour cost showing the cost per day (8 hours
| (a) | Monthly salary: Rs 900 |
| (b) | Leave salary: 5% of (a) |
| (c) | Employer's contribution to PF: 8 ½% of (a) and (b) |
| (d) | Employer's contribution to ESI: 3% of (a) and (b) |
| (e) | Pro rata expenditure on amenities to labour: Rs 112 per head per month |
| (f) | Number of working hours in a month of 25 days: 8 hours per day |
[Madras, B. Com. (ICE) C & M, May 1999]
[Ans: cost per day = Rs 46.63]
Illustration 16
Labour hourly rate: Calculate the labour hour rate of a worker P from the following data:
| Basic pay | Rs 300 per month |
| DA | Rs 250 per month |
| Fringe benefits | Rs 150 per month |
Number of working days in a year is 300. Thirty days with full-pay leave and 20 days with half-pay leave in a year are availed and allowed. Assume 8-hour days. What would be the effect on hourly rate if only 30 days full pay leave is allowed?
Solution:
| (a) Effective working hours | |
| Working days in a year | 300 |
| Less: leave days (30 + 20) | 50 |
| Effective working days | 250 |
| Working hours in a day | 8 hours |
(i) Total effective working hours: 250 × 8 = 2,000 hours
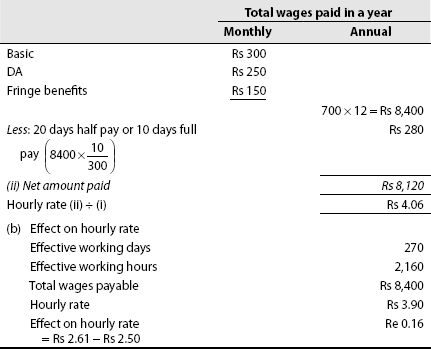
Problem 16. Calculate the labour cost per hour for a worker from the following information
| Basic pay | Rs 200 per month |
| DA | Rs 150 |
| House rent allowance | Rs 100 |
| Number of working days per year—300 | |
| Leave rules | |
| 30 days paid leave (PL) with full pay | |
| 20 days sick leave (SL) with half pay |
Usually, sick leave is fully availed of.
[Madras, B.Com., March 1988]
[Ans: labour cost per hour = Rs 2.34; net labour cost per year = Rs 4,680; effective working days per annum = 250]
Hint: Assume a normal working day of 8 hours.
Illustration 17
Calculate the amount of wages and bonus for a worker from the following particulars:
| Job commenced: Monday, 24 December 1994 at 8 a.m. |
| Job finished: Saturday, 29 December 1994 at 1 p.m. |
| Quantity of work turned out: 638 |
| Quantity of pieces passed: 600 |
| Worker's rate: Rs 6.00 per hour |
| Time allowed: 10 pieces per hour |
| Bonus: 40% of time saved |
Assume that the employee worked for 9 hours a day and that there was no overtime.
Solution:
Time taken:
| Monday to Friday: 5 days, 9 hours per day | 45 hours |
| Saturday: 8 a.m. to 1 p.m. | 5 hours |
| 50 hours | |
| Standard time for 600 pieces at 10 pieces per hour | 60 hours |
| Time saved | 10 hours |
Wages for time taken:

Problem 17. The allowed time for a job was fixed as 1 hour by applying the principles of time and motion studies, but the job was completed in 40 minutes. Calculate the wages under the three methods of payment and find the cost per article, assuming the basic time rate of Rs 5 per hour.
[B. Com., Bangalore, Bombay]
[Ans: piece rate = Rs 5.00; Halsey = Rs 4.16; Rowan = Rs 4.44]
Illustration 18
What will be the earnings of a worker at Rs 6.50 per hour when the worker takes 140 hours to do a volume of work for which the standard time allowed is 200 hours. The plan of bonus is on sliding scale as unde
| Bonus within the first 10% of saving in standard time | 40% of time saved |
| Bonus within the second 10% of saving in standard time | 50% of time saved |
| Bonus within the third 40% of saving in standard time | 50% of time saved |
| Bonus within the fourth 10% of saving in standard time | 70% of time saved |
| Bonus for the rest | 75% of the time saved |
Solution:
Time saved = 200 hours − 140 hour = 60 hour
Basic wages = 140 hours × Rs 6.50 = Rs 910.00
Bonus:
| First 10% of 60 hours: 6 hours at 40% | 2.40 hours |
| Next 10% of 60 hours: 6 hours at 50% | 3.00 hours |
| Next 40% of 60 hours: 24 hours at 50% | 12.00 hours |
| Next 10% of 60 hours: 6 hours at 70% | 4.20 hours |
| Rest 30% of 60 hours: 18 hours at 75% | 13.50 hours |
| 100% 60 hours | 35.10 hours |
| 35.10 hours at Rs6.50 | 228.15 |
| Total earnings | Rs 1138.15 |
Problem 18. In a manufacturing concern, bonus to workers is paid on a slab rate based on cost saving towards labour and overheads. The following are the slab rates:
| Up to 10% saving | 5% of earnings |
| Up to 15% saving | 9% of earnings |
| Up to 20% saving | 13% of earnings |
| Up to 30% saving | 21% of earnings |
| Up to 40% saving | 28% of earnings |
| Above 40% saving | 32% of earnings |
The wage rates per hour of four workers P, Q, R and S are Re 1, Rs 1.10, Rs 1.20 and Rs 1.40, respectively. Overhead is recovered on direct wages at the rate of 200%. The standard cost under wages and overhead per unit of production is fixed at Rs 30. The workers completed one unit each in 8, 7, 5½ and 5 hours, respectively. Calculate the following for each worker
| (a) | Amount of hours earned |
| (b) | Total earnings |
| (c) | Total earnings per hour |
[Madras, B.A. Corp. C & M, March 1997]
[Ans: (a) P = Rs 8, Q = Rs 7.70, R = Rs 6.6, S = Rs 7; (b) P = Rs 9.04, Q = Rs 9.32, R = Rs 8.45, S = Rs 8.47; (c) P = Rs 1.13, Q = Rs 1.33, R = Rs 1.536, S = Rs 1.694]
6.16 ADVANCED-TYPE SOLVED PROBLEMS
- Calculate the earnings of workers A and B from the following particulars for a month and allocate the earnings to each job X, Y and Z
A B (a) Basic wages Rs 200 Rs 200 (b) DA 50% 55% (c) PF (on basic wages) 8% 8% (d) ESI (on basic wages) 2% 2% (e) Overtime 10 hours – (f) Idle time and leave – 16 hours The normal working hours for the month are 200 hours. Overtime is paid at double the normal wage plus DA. Employer's contributions to ESI and PF are at equal in rate with employee's contributions. The month contains 25 working days and one paid holiday. The two workers were employed on jobs X, Y and Z in the following proportions:
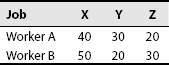
Overtime was done on job Y.
Solution: Statement showing the earnings of workers
A (Rs) B (Rs) Basic wages 200 200 DA 100 110 Overtime wages 30 – Gross wages earned 330 310 Less: Employee's contribution to PF 16 16 Employee's contribution to ESI 4 4 Net wages due 310 290 Statement of labour cost Gross wages (excluding overtime) 300 310 Employer's contribution to PF and ESI 20 20 320 330 Labour cost per hour 1.60 1.65 Allocation of wages to jobs:

- A factory department has 180 workers who are paid an average wage of Rs 17.50 per week (48 hours) and DA per month (208 hours) of Rs 130. PF deduction is at 8% on gross, of which 1 1/6% is for family pension fund for half the number of workers, and ESI is at Rs 1.25 for each worker. The employer contributes an equivalent amount. The company gives only the minimum bonus of 8 1/3% and allows statutory leave of 2 weeks per year with pay. Show the weekly wage summary for the financial books from the departmental labour hour costs for job costing.
Solution:
Weekly wage summary:
Wages (180 workers at Rs 17.50 each) Rs 3,150.00 DA (48/208 × Rs 130 × 180) Rs 5,400.00 Rs 8,550.00 Bonus (8 1/3% of Rs 8,550) Rs 712.50 Rs 9,262.50 Less: PF contribution (8% -1 1/6% of Rs 8,550) Rs 584.00 Family pension (1/2 of 1 1/6 of Rs 8,550) Rs 50.00 ESI contribution at Rs 1.25 per worker Rs 225.00 Rs 859.00 Net wages Rs 8,403.50 Computation of departmental labour cost:
Wages 3,150.00 DA 5,400.00 Bonus 712.50 PF contribution (584 + 50) 634.00 ESI contribution 225.00 Leave pay (8,550 × 2/52) 328.50 Total labour cost 10,450.00 
- In a factory, Raja and Ram produce the same product using the same input material at the same normal wage rate. Bonus is paid to both of them according to normal time wage rate adjusted by the proportion of time saved to standard time for the completion of the product. Time allotted to producing the product is 50 hours. Raja takes 30 hours and Ram takes 40 hours to produce the product. The factory costs of the product for Raja are Rs 6,200 and for Ram Rs 6,560. The factory overhead rate is Rs 24 per man-hour.
Calculate the (a) normal wage rate, (b) cost of material used for producing the product and (c) input of material if the unit material cost is Rs 32.
Solution:
Factory cost of Raja
Material x Wages 30y Bonus (40g × 10/50) 12y Overheads 720 x + 30y + 12y + 720 Factory cost of Ram
Material x Wages 40y Bonus (40g × 10/50) 8y Overheads 960 x + 40y + 8y + 960 

- Two fitters, a labourer and a boy, undertake a job on piece rate for Rs 1,290. The time spent by each of them is 220 ordinary working hours. The rates of pay on time rate basis are Rs 1.50 per hour for each of the two fitters, Re 1 per hour for the labourer and Re 0.50 per hour for the boy. Calculate the following:
- The amount of piecework premium and the share of each worker when the piecework premium is divided proportionately to the time wages paid.
- The selling price of the aforementioned job on the basis of the following additional data: Cost of direct material is Rs 2,010. Works overhead is 20% of prime cost. Selling overhead is 10% of works cost, and profit is 25% on the cost of sales.
Solution:
- Computation of wages:

- The amount of piecework premium:
Piecework wages = Rs 1,290
Time rate wages = Rs 990
Piecework premium = Rs 300
- Apportionment of piecework premium:
Ratio = 330:330:220:110
Fitter 1 = 100
Fitter 2 = 100
Labourer = 67
Boy = 33
- Selling price:
Direct material = Rs 2,010
Direct wages = Rs 1,290
Prime costs = Rs 3,300
Works overhead = Rs 660
Factory cost = Rs 3,960
Selling overhead = Rs 396
Cost of sales = Rs 4,356
Profit = Rs 1,089
Sales = Rs 5,445
- Following are the particulars for March 2000 relating to four employees working in department A of a factory exclusively for job number 130:

The normal working hours per week of 6 days are 48, or 8 hours per day. All Sundays are paid holidays. (There are no other holidays during the month.)
PF contribution was 8% of monthly wages by employees.
PF contribution was 8% of monthly wages by the employer.
ESI contribution was 3% of monthly wages by employee and 5% of monthly wages by the employer.
From the foregoing data, calculate the following:
- Net monthly wages payable by the employer.
- The total amount of PF contribution to be deposited by the employer.
- ESI contribution to be deposited by the employer.
- Total labour cost to the employer for the month of April, chargeable to the job
- Total cost of the job including the cost of materials valued at Rs 6,000 overheads at 50% of prime cost.
Solution:
(a) Calculation of net wages payable for the month Gross wages for the month (a) Foreman at Rs 800 per month Rs 800.00 (b) Mechanic at Rs 15 per day × 30 days Rs 450.00 (c) Machine operator at Rs 12 per day × 30 days Rs 360.00 (d) Worker at Rs 10 per day × 30 days Rs 300.00 Rs 1,910.00 Less: deductions PF contribution at 8% at Rs 1,910 by employees Rs 152.80 ESI contribution at 3% of Rs 1,910 by employees Rs 57.30 Net wages payable Rs 1,699.90 (b) Employer's share of PF (8% of Rs 1,910) Rs 152.80 Employer's share of PF (8% of Rs 1,910) Rs 152.80 Total amount of PF contribution to be deposited by the employer Rs 305.60 (c) Employer's share of ESI (5% of Rs 1,910) Rs 95.50 Employer's share of ESI (3% of Rs 1,910) Rs 57.30 ESI contribution to be deposited by the employer Rs 152.80 (d) Total labour cost to the employer: Total gross wages Rs 1,910.00 Add: employer's contribution towards PF Rs 152.80 Employer's contribution towards ESI Rs 95.50 Rs 2,158.30 (e) Total cost of job Material Rs 6,000.00 Labour cost Rs 2,158.30 Prime cost Rs 8,158.30 Overheads at 50% of prime cost Rs 4,079.15 Total cost of job Rs 12,237.45 - A, B and C in a particular day produced 200, 250 and 300 pieces, respectively, of a product P. Time allowed for the production of 25 units of P is 1 hour and the hourly rate of wage payment is Rs 8. Calculate for each of these three workers the following under Halsey's premium bonus (50% sharing) and Rowan's premium bonus methods of labour remuneration:
- Earnings for the day (8 hours per day) and
- Effective rate of earnings per hour
Solution: Workers

(i) Computation of earnings per day
(a) Halsey's premium bonus method:
Earnings = hourly rate × time taken + time saved/2
A B C 8 × 8 8 × 8 + (8 × 2/10) 8 × 8 (8 × 8 × 4/12) Rs 64 Rs 76.80 Rs 85.33 - Computation of effective rate of earnings per hour:

- A job can be calculated using either worker A or worker B. A takes 32 hours to complete the job, whereas B finishes it in 30 hours. The standard time to finish the job is 40 hours. The hourly wage rate is the same for both the workers. In addition, worker A is entitled to bonus according to Halsey's plan (50% sharing), whereas B is paid bonus as per Rowan's plan. Cost of the job comes to Rs 2,600 irrespective of the worker engaged. Find out the hourly wage rate and cost of raw materials input. Also, show the cost against each element of cost included in factory cost.
Solution:
- Computation of time saved and wages:
Workers A B Standard time (hours) 40 40 Actual time (hour) 32 30 Time saved (hour) 8 10 Wages paid for time taken at Rs x per hour (Rs) 32x 30x - Computation of bonus:

- Computation of total works:
Worker A: 32 + 4x = 36x
Worker B: 30x + 7.5x = 37.5x
- Computation of factory cost of the job:
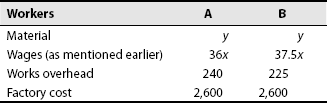
From the aforementioned information, the following simultaneous equations can be written:
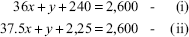
On submitting equation (i) from equation (ii), we get the following results:
15x – 15.x = 0or
1.5x = 15or
x = Rs 10 per hourOn substituting the value of x in equation (1), we get
36 × 10 + y + 240 = 2,600or
y = 2,600 – 360 – 240or
y = Rs 2,000The wage rate per hour is Rs 10 and the cost of raw material input is Rs 2,000 for the job.
- Calculate the earnings of workers A, B and C under the straight piece-rate system and Merrick's piece-rate system from the following particulars:
Normal rate per hour: Rs 2.70
Standard time per unit: 1 minute
Output per day is as follows:
Worker A: 390 units
Worker B: 450 units
Worker C: 600 units
Working hours per day are eight.
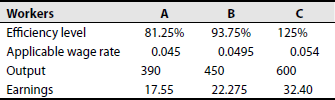
Solution:
Basic calculations:
Normal rate per hour: Rs 2.70
Standard rate per hour: 60 units
Piece rate per unit (2.7/60): 0.045 paise
Efficiency level:
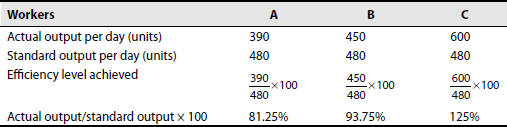
Up to 83% efficiency = Ordinary piece rate
83% to 100% efficiency = 110% of ordinary piece rate
Over 100% efficiency = 120% of ordinary piece rate
Statement of earnings of workers under Merrick's multiple piece-rate system:
- Two workers, Ram and Raju, produce the same product using the same material. Their normal wage rate is also the same. Ram is paid bonus according to the Rowan system, whereas Raju is paid bonus according to the Halsey system. The time allowed to finish the product is 100 hours. Ram takes 60 hours, whereas Raju takes 80 hours to complete the product. The factory overhead rate is Rs 10 per man-hour actually worked. The factory cost for the product for Ram is Rs 3,640 and for Raju is Rs 3,800.
You are required to do the following:
- Find the normal rate of wages
- Find the cost of materials
- Prepare a statement comparing the factory cost of the products as made by the two workers.
Solution:
Basic calculations:
Let x be the cost of material and y be the normal rate of wages per hour.
Factory cost of worker Ram:
Material x Wages 60y Bonus (60y × 40/100) 24y Overheads 600 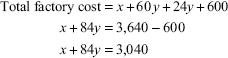
Factory cost of worker Raju:
Material x Wages 80y Bonus (20y × 50/100) 10y Overheads 800 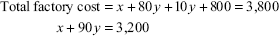
The two simultaneous equations can be solved as follows to ascertain the values of x and y:
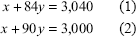
On subtracting equation (1) from equation (2), we get
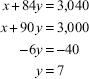
On putting the value of y in equation (1), we get
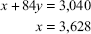
- y was presumed the normal wage rate. Hence, the normal wage rate per hour is 7.
- x was presumed the cost of material. Hence, its value is Rs 3,628.
Comparative statement of the factory costs of the products made by the two workers:
Ram Raju Material cost 3,628 3,628 Direct wages 420 560 Bonus 168 70 Factory overheads 600 800 Factory costs 3,640 3,800
CHAPTER SUMMARY
After reading this chapter one must understand that labour is the second most important cost component of a product. Labour cost has certain special features, and controlling it involves facing some peculiar difficulties. Thus, different incentive schemes are used. Labour cost is also important in the light of controlling labour turnover.
KEY FORMULAE
Calculation of labour turnover
-
- Separation method = number of separations during a period/average number of workers during a period × 100.
- Replacement method = number of replacements during a period/number of workers during a period × 100.
- Flux method = number of separations + number of replacements/average number of workers during a period × 100.
- Skill dilution index = number of persons over four years of service at present/total employees × 100.
- Skill wastage index = number of persons over four years of service at present/total employees four years ago × 100.
- Level of activity = actual production in standard hours/budgeted hours.
- Labour efficiency = actual production in standard hours/actual hours worked.
- Labour cost per unit = direct wages/total number of units.
- Labour utilization = actual hours/available hours.
- Absenteeism = number of absentees/average number of employees.
- Accident frequency per week = number of accidents to date/number of weeks to date.
- Illness = hours lost due to illness/total labour hours.
- Labour productivity = production in standard hours/actual hours.
- Earnings under time rate = hours worked × rate per hour.
- Earnings under the straight piece-rate system = number of units × rate per unit.
- Earnings under Taylor's differential piece-rate system = low piece rate if actual output is below the standard value and high piece rate if actual output is above standard.
- Merrick's differential piece-rate system.
Output payment
Up to 83% ordinary piece rate
83% to 100%: 110% of ordinary piece rate
Above 100%: 120% of ordinary piece rate
Labour
- Gantt's task and bonus plan
Output payment
Output below standard time rate
Output at standard 20% bonus on time rate
Output above standard high piece rate on the entire output
- Halsey's premium plan:
Earnings = hours worked × rate per hour + 50% of time saved × rate per hour
- Rowan system:
Earnings = hours worked × rate per hour + time saved / time allowed in hours worked × rate per hour
- Barth variable-sharing plan:
Earnings = rate per hour × square root of standard hours of actual hours
- Emerson's efficiency bonus:
Earnings = actual hours × rate per hour + bonus percentage × hours worked × rate per hour
Bonus calculation
Efficiency bonus
Up to 66 2/3%: no bonus
66 2/3–% to 100%: up to 20% bonus
Above 100%: 20% + 1% for every 1% increase in efficiency
EXERCISE FOR YOUR PRACTICE
Objective-Type Questions
I. State whether the following statements are true or false:
- Timekeeping and time booking are the same.
- The idle-time report should show normal idle time separately from abnormal idle time.
- For reducing labour cost per unit, a high input-to-output ratio is important.
- Productivity of workers can be improved only if they are supervised closely.
- Time and motion study refers to a study to establish a proper method and time.
- Labour once lost cannot be recouped.
- Time and motion study is conducted by the payroll department.
- Job evaluation and job analysis are the same.
- Labour cost is a second major element of cost.
- The human element in labour makes the control of labour cost difficult.
[Ans: 1—false, 2—true, 3—true, 4—false, 5—true, 6—false, 7—true, 8—true, 9—true, 10—true]
II. Choose the correct answer:
- Time and motion study is conducted by
- Payroll department
- Personnel department
- Timekeeping department
- Engineering department
Ans: (d)
- Wage sheet is prepared by
- Cost accounting department
- Payroll department
- Personnel department
- Timekeeping department
Ans: (b)
- Cost of normal idle time is charged to
- Factory overhead
- Office overhead
- Selling overhead
- Administrative overhead
Ans: (a)
- Under Emerson's efficiency plan, the worker gets wages at
- 100% efficiency
- 80% efficiency
- 33 1/3% efficiency
- 66 2/3% efficiency
Ans: (c)
- Under Gantt's task and bonus plan, no bonus is available to a worker if his or her efficiency is lower than
- 100%
- 50%
- 75%
- 66 2/3%
Ans: (a)
- The system that combines both time and piece rate is
- Emerson's system
- Merrick's differential system
- Halsey system
- Bedaux system
Ans: (a)
- The wage system that benefits the less-efficient workers is
- Time wage
- Piece rate
- Halsey's system
- Rowan's system
Ans: (a)
- The method of remuneration that gives stability of labour cost to the employer is
- Group bonus scheme
- Measured day work
- Premium bonus system
- Straight piece rate
Ans: (b)
- Incentive method of wage payment used for indirect workers is
- Gantt's task and bonus plan
- Rowan's plan
- Taylor's differential piece-rate system
- None of the above
Ans: (d)
- Under the high wage plan, a worker is paid
- Normal wage plus bonus
- At a double rate for overtime
- According to his or her efficiency
- At a time rate higher than the usual rate
Ans: (d)
DISCUSSION QUESTIONS
Short Answer-Type Questions
- What do you understand by the term labour turnover?
- What do you mean by labour?
- Discuss the possible effects of labour turnover.
- Enumerate the causes of labour turnover
- Write notes on (a) time study and (b) motion study.
- What is idle time?
Essay-Type Questions
- Discuss the advantages and disadvantages of the following methods of Remuneration: (a) time rate and (b) piece rate.
- How would you treat the following in cost: (a) overtime, (b) leave with pay, (c) idle time and (d) might shift allowance?
- Explain the causes of idle time.
- When is overtime premium charged as an indirect manufacturing cost?
- Distinguish between direct and indirect labour costs.
- Bring out the merits and demerits of the piece-rate system.
- What are the essential features of a sound wage incentive plan?
- Write about some important incentive wage plans.
PROBLEMS
- Rajan Ltd. follows Taylor's differential piece-rate system, 80 and 120 being the differentials for below-standard and above-standard work. From the following data, ascertain the earnings of workers X and Y:
Standard time: 15 minutes per unit Time worked: 8 hours Units produced: X—28 Y—35 Normal piece rate per unit: Rs 2 [Ans: earnings of X = Rs 44.80; earnings of Y = Rs 84.00]
- From the following particulars, calculate the earnings of workers A and B under the piece-rate system:
Standard time allowed: 10 units per hour Normal time rate per hour: Re 1 Differential to be applied: 80% of piece rate when below standard 120% of piece rate at or above standard In a day of 8 hours, A produced 75 units B produced 100 units [Madras, 1999]
[Ans: earnings of workers:]
A (Rs) B (Rs) Straight piece rate 7.5 10 Taylor's differential piece rate 6 12 - Calculate the earnings of workers A and B under the straight piece-rate system and Taylor's differential piece-rate system from the following particulars:
Normal rate per hours: Rs 1.80 Standard time per unit: 20 seconds Differentials to be applied: 80% of piece rate below standard 120% of piece rate at or above standard Worker A produces 1,300 units per day, and worker B produces 1,500 units per day [Madras, 1989]
[Ans: earnings of workers]
A B (Rs ps.) (Rs ps.) Straight piece-rate system 13.00 15.00 Taylor's differential piece-rate system 10.40 18.00 Hint: Assume normal working day of 8 hours.
- Set out a comparative statement showing the effect of paying wages on (a) Halsey and (b) Rowan premium plans assuming the following:
Standard time: 10 hours Hourly wage rate: Rs 5 Time taken: 8 hours Overhead rate per hour: Rs 6 [B. Com., Bangalore]
[Ans: wages are (a) Rs 45 and (b) Rs 48; employer's savings are (a) Rs 17 and (b) Rs 14]
- A worker takes 9 hours to complete a job on daily wages and 6 hours on a scheme of payment by results. His day rate is Rs 7.50 an hour, the material cost of the product is Rs 40 and the overheads are 150% of the total direct wages. Calculate the factory cost of the product under (a) piecework plan, (b) Rowan plan and (c) Halsey plan.
[B. Com., Bombay]
[Ans: (a) Rs 208.75, (b) Rs 190.00, (c) Rs 180.63]
- The standard time allowed for a job is 50 hours. The hourly rate of wages is Rs 4.00 plus a DA of 25 paise per hour worked. The actual time taken by the worker was 40 hours. Calculate the earnings per hour worked under Halsey's premium plan and Rowan's plan.
[B. Com., Madurai]
[Ans: total earnings and hourly rate under Halsey are Rs 190.00 and Rs4.75; total earnings and hourly rate under Rowan are Rs 202.00 and Rs5.05]
- What earnings will a worker receive under Halsey's plan and Rowan's plan if he executes a piece of work in 60 hours as against 75 hours allowed? His hourly rate is Rs 2.00 and he is paid 50% of the time saved under Halsey's plan. He gets a DA of Rs 8.00 per day of 8 hours worked, in addition to his wages.
[B.Com.]
[Ans: under Halsey's plan = Rs 195; under Rowan's plan = Rs 204]
Merrick's Multiple Piece-rate System
- Calculate the earnings of three workers A, B and C under Merrick's plan of piece-rate system, given the following:
Standard production: 120 units Production of A: 90 units Production of B: 100 units Production of C: 130 units Ordinary piece rate: Re 0.10 [Madras, 1999]
[Ans: earnings of workers—A = Rs 9.00, B = Rs 11.00 and C = Rs 15.60]
- On the basis of the following information, calculate the earnings of A, B, C and D under Merrick's differential piece-rate system:
Standard production per hour: 12 units Normal rate per hour: Re 0.60 In an 8-hour day: A produced 64 units, B produced 96 units, C produced 84 units and D produced 100 units [Madras, 1991]
[Ans: earnings of workers—A = Rs 3.20, B = Rs 5.28, C = Rs 4.62 and D = Rs 6.00]
Hint: At 100% efficiency also, 110% of the ordinary piece rate applies.
Halsey's Plan
- Calculate the earnings of a worker from the following information as per Halsey's plan:
(a) Standard time: 12 hours; Actual time: A—10 hours, B—8 hours and C—6 hours Hourly rate: Rs 8. (b) Hourly rate of wages: Rs 10 Standard time for the production of a dozen units of a product = 2 hours Actual time taken by the worker to produce 25 dozens: 40 hours (c) Articles manufactured by S, a worker in a factory: 300 Standard time allowed: 10 minutes per unit Actual time: 44 hours Standard rate: Rs 5 per hour [Ans: earnings of workers: (a) A = Rs 88, B = Rs 80, C = Rs 72; (b) Rs 450; (c) Rs 235]
- A worker takes 9 hours to complete a job on daily wages and 6 hours on a scheme of payment by results. His daily rate is Rs 7.50 per hour. The material cost of the product is Rs 40 and the overheads are recovered at 150% of the total direct wages. Calculate the factory cost of the product under (a) piecework plan, (b) Halsey's plan and (c) Rowan's plan.
[B. Com., Bombay]
Ans:

- Calculate the earnings of A and B under the straight piece-rate basis and Taylor's differential piece-rate system from the following information:
Standard production: 10 units per hour Factory day: 8 hours Normal time rate: Rs 5 Differential rates to be applied: 80% of piece rate below standard 120% of piece rate at or above standard A produced 70 units in a day B produced 85 units in a day [B. Com., Madurai]
[Ans: under straight piece rate, A gets Rs 35 and B gets Rs 42.50; under Taylor's differential system, A gets Rs 28 and B gets Rs 51]
- In a manufacturing concern, the daily wages guaranteed for workers is Rs 20. The standard output for the month is 1,000 articles, representing 100% efficiency. The rate of wages is paid without bonuses to those workers who show up to 66 2/3% efficiency. Beyond this, bonus is payable in a graded scale:
Efficiency Bonus 90% 10% 100% 20% There is an increase of 1% of bonus for every 1% further rise in efficiency. Calculate the total earnings of A, B, C and D who worked 26 days in a month, with outputs 500; 900; 1,000; and 1,200 articles, respectively.
[B.Com., Mysore]

- The standard output of a product has been fixed at 6 units in a day of 8 hours. The normal wages per day is Rs 12. Determine the total wages including bonus payable under Halsey's plan when the outputs are 5, 8, 12 and 15 units, respectively, per day. Also calculate the labour cost per unit.
[Madras, 1998]
[Ans: total wages including bonus and labour cost per unit for different outputs: 5 units—Rs 12 and Rs 2.4 per unit; 8 units—Rs 14 and Rs 1.75 per unit; 12 units—Rs 18 and Rs 1.5 per unit; 15 units—Rs 21 and Rs 1.4 per unit]
Rowan's Plan
- A worker earns Rs 2 as bonus on a job that requires 20 standard hours at Re 0.50 per hour, under Halsey's incentive system based on the ratio 50:50. What would be his earnings under Rowan's plan?
[Madras, 1986]
[Ans: earnings under Rowan's plan = Rs 8.40; actual hours worked = 12]
- From the following particulars, work out the earnings for the week of a worker under (a) straight piece-rate system, (b) differential piece-rate system, (c) Halsey's premium system and (d) Rowan's system:
Number of working hours per week: 48 Wages per hour: Rs 3.75 Normal time per piece: 20 minutes Rate per piece: Rs 1.50 Normal output per week: 120 pieces Actual output for the week: 150 pieces Differential piece rate: 80% of piece rate when output is below standard and 120% when output is above standard.
[Madras, 1990]
[Ans: earnings of worker for the week: (a) Rs 225, (b) Rs 270, (c) Rs 183.75 and (d) Rs 187.20; standard time for the output = 50 hours =
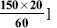
- From the following particulars, you are required to work out the earnings of a worker for a week under (a) straight piece-rate system, (b) differential piece-rate system, (c) Halsey's premium scheme (50% saving) and (d) Rowan's premium scheme:
Weekly working hours 48 Hourly wage rate Rs 7.50 Piece rate per unit Rs 3 Normal time taken per piece 20 minutes Normal output per week 120 pieces Actual output for the week 150 pieces Differential piece rate is 80% of piece rate when output is below normal and 120% of piece rate when output is above normal.
[Madras, 1999]
[Ans: earnings of the worker for the week: (a) Rs 450, (b) Rs 540, (c) Rs 367.5, (d) Rs 374.40]
Emerson's Efficiency Plan
- From the following information, calculate the bonus and earnings under Emerson's efficiency bonus plan:
Standard output in 12 hours 192 units Actual output in 12 hours 168 units Time rate Re 0.75 per hour If the actual output is 240 units, what will be the amount of bonus and earnings?
[Madras, 1991]
[Ans: (a) bonus and earnings when actual output is 168 units: bonus = Re 0.72 and earnings = Rs 9.72; (b) if actual output is 240 units, bonus = Rs 4.05 and earnings = Rs 13.05]
Hint: Bonus at 87.5% efficiency is 8% under Emerson's scheme.
- On the basis of the following information, calculate the earnings of X and Y under the straight piece-rate system and Taylor's differential piece-rate system:
Standard production: 10 units per hour Normal time rate: Rs 5.00 Differential piece rate to be applied: 80% of piece rate for performance below standard 120% of piece rate for performance at or above the standard Actual performance: X produced 80 units in a day of 10 hours Y produced 110 units in a day of 10 hours [B. Com., Calicut]
[Ans: straight piece rate: X—Rs 32, Y—Rs 66; differential piece rate: X—Rs 40, Y—Rs 55]
- In a manufacturing company, the daily wage rate guaranteed for a worker is Rs 25 and the standard output fixed for the month is 1,000 units, representing 100% efficiency. The daily wage rate is paid without bonus to those workers who meet up to 66.3% the set efficiency standard. Beyond this, there is a bonus payable in a graded scale in a fixed ratio to the increased output as under:
Efficiency Bonus payable 90% 10% 100% 20% There is an increase of 1% for every 1% further rise in efficiency. Find the total earnings of A, B, C and D who have worked 26 days in a month. The workers’ outputs are A—500 units, B—900 units, C—1000 units and D—1,100 units.
[B. Com., Punjab]
[Ans: A—Rs 650, B—Rs 715, C—Rs 780, D—Rs 845]
Bedeaux's Point System
- In a 10-hour working day, standard output is fixed as 100 units. The Bedeaux's point system is under operation. A worker produced 120 units during the day. The normal time rate is Rs 20 per hour. Ascertain the earnings of the worker for the day under Bedeaux's point system.
[Ans: earnings = Rs 230 (200 + 30)]
Barth's Variable-sharing Plan
-
Standard time for a job 50 hours Actual time taken 40 hours Standard rate per hour Rs 10 Calculate wages as per Barth's variable-sharing plan.
- Calculate the earnings of a worker under (a) Rowan's premium bonus system and (b) Halsey–Weir premium bonus system (50% of the time saved) from the following particulars:
(a) Hourly rates of wages (guaranteed): Rs 5.00 (b) Standard time for producing one dozen articles: 3 hours (c) Actual time taken by the worker to produce 20 dozen articles: 48 hours [B.Com., Nagarjuna]
[Ans: (a) Rs 288; (b) Rs 270]
- Calculate the earnings of workers A and B under (a) straight piece-rate system and (b) Taylor's differential piece-rate system from the following particulars:
Normal rate per hour: Rs 2.40 Standard time per unit: 30 seconds Differentials to be applied: 80% of piece rate below standard 120% of piece rate at or above standard Worker A produces 800 units per day and B produces 1,000 units per day.
[Ans: (a) A—Rs 16 and B—Rs 20; (b) A—Rs 17.6 and B—Rs 24]
- From the following particulars, calculate the earnings of two workers, A and B, under (a) straight piece-rate system and (b) Taylor's differential piece-rate system:
Standard time per unit: 36 seconds Normal rate per hour: Rs 9 Differential rates to be applied: 80% of piece rate when below standard 120% of piece rate at or above standard The workers have produced in a day of 8 hours as follows: A—700 units B—900 units [B. Com., Bombay]
[Ans: (a) A—Rs 63 and B—Rs 81; (b) A—Rs 69.3 and B—Rs 97.20]
- What will be the earnings of a worker at Re 0.55 per hour when he takes 140 hours to do a volume of work for which the standard time allowed is 200 hours? The plan of payment of hours is on a sliding scale as under
Within the first 10% saving in standard time, bonus is 40% of the time saved. Within the second 10% saving in time, bonus is 50% of the time saved. Within the third 10% saving in standard time, bonus is 60% of the time saved. Within the fourth 10% saving in standard time, bonus is 70% of the time saved. For the rest, bonus is 75% of the time saved. [Madras, 1992]
[Ans: time wages = 140 × 0.55 = Rs 77; bonus for 30 hours = 30 × 0.55 = Rs 16.5; total earnings = Rs 93.5]
Hint: Time saved = 200 − 140 = 60 hours; 10% in standard time = 20 hours.

Group Bonus Schemes
- In an assembly shop of a motorcycle factory, four workers A, B, C and D work together as a team and are paid on group piece rate. They also work individually on day-rate jobs. In a 44-hour week, the following hours have been spent by A, B, C and D on group piecework, viz, A—40 hours, B—40 hours, C—30 hours and D—20 hours. The balance of the time has been worked by each worker on day works jobs. Their hourly rates are: A—0 paise, B—75 paise, C—Re 1 and D—Re 1.
The group piece rate is Re 1 per unit and the team has produced 150 units. Calculate the gross weekly earnings of each worker taking into consideration that each individual is entitled to a DA of Rs 20 per week.
[Calcutta, B.Com.]
[Ans: gross weekly earnings: A—Rs 52, B—Rs 68, C—Rs 79, D—Rs 74; group bonus: A—Rs 10, B—Rs 15, C—Rs 15, D—Rs 10; individual wages: A—Rs 2, B—Rs 3, C—Rs 14, D—24; group work wages: A—Rs 20, B—Rs 30, C—Rs 30, D—Rs 20; DA: A—Rs 20, B—Rs 20, C—Rs 20, D—Rs 20]
Hint: Group bonus is divided in the ratio of group work wages.
- In a factory, group bonus system is in use, which is calculated on the basis of earnings under time rate.
The following particulars are available for a group of four workers P, Q, R and S:
Output of the group: 16,000 units
Piece rate per 100 units: Rs 2.50, in addition to time wages

Calculate the bonus and total wages earned by each worker.
[Ans: bonus: P—Rs 90, Q—Rs 90, R—Rs 120, S—Rs 100; total wages: P—Rs 162, Q—Rs 162, R—Rs 216, S—Rs 180]
- From the following particulars, find the amount of cash required for giving wages in a factory for a particular month:
(i) Wages for normal hours worked Rs 20,500 (ii) Wages for overtime Rs 2,200 (iii) Leave wages Rs 2,700 (iv) Deduction of employees’ share to state insurance Rs 500 (v) Employee's contribution to PF Rs 1,600 (vi) House rent is to be recovered from 30 employees at the rate of Rs 10 per month [I.C.W.AInter]
[Ans: Rs 22,000]
- From the following particulars, you are required to prepare a statement of labour cost showing the cost per day:
(i) Monthly salary: Rs 1,350.00 (ii) Leave salary: 5% of salary. (iii) Employer's contribution to PF: 8.5% of (i) and (ii) (iv) Employer's contribution to state insurance: 3% of (i) and (ii) (v) Pro rata expenditure on amenities to labour: Rs 75 per head per month (vi) Number of working hours in a month: 200 (assuming 8-hour day) [B. Com., Banglaore]
[Ans: Rs 66.22]
- From the following particulars, prepare the labour cost per man-day of 8 hours:
(a) Basic salary: Rs 55 per day (b) DA: Re 0.50 per every point over 100 (cost of living index for working class); current cost of living index is 700 points. (c) Leave salary: 10% of (a) and (b) (d) Employer's contribution to PF: (a) + (b) + (c) (e) Employer's contribution to state insurance: 2.5% of (a) + (b) + (c) (f) Expenditure on amenities to labour: Rs 20 per head per month (g) Number of working days in a month: 25 days of 8 hours [ICWA Inter]
[Ans: Rs 82.20]
Cash Required for Wage Payment
- From the following details, ascertain the amount of cash required for the payment of salaries in a firm for the month of January:
(1) Normal time salaries: Rs 65,000 (2) DA: 20% of (1) (3) Leave wages: 5% of (1) and (2) (4) Employee's contribution to ESI and PF: 3% and 5% respectively on (1) and (2) (5) Income tax deduction at source: Rs 4,000 (6) Deduction for insurance premium: Rs 5,000 (7) Festival advance must be recovered from 60 employees at Rs 100 per employee. [Ans: cash required for payment of salaries = Rs 60,660]
- From the following particulars, prepare a statement showing the labour cost per man-day of 8 hours:
(a) Basic salary: Rs 2 per day (b) DA: 25 paise for every point over 100 (cost of living index for working class); current cost of living index is 700 points (c) Leave salary: 10% of (a) and (b) (d) Employer's contribution to PF: 8% of (a), (b) and (c) (e) Employer's contribution to state insurance: 2.5% of (a), (b) and (c) (f) Expenditure on amenities to labour: Rs 20 per head per mensem (g) Number of working days in a month: 25 days of 8 hours each [Madras, 1993]
[Ans: labour cost per man-day = Rs 10.52, per month = Rs 263.10]
- From the following particulars, calculate the labour cost per man-day of 8 hours:
(a) Basic salary: Rs 5 per day (b) DA: 20 paise per every point over 100 (cost of living index for workers); current cost of living index is 800 points. (c) Leave salary: 5% of (a) and (b) (d) Employer's contribution to PF: 8% of (a) and (b) (e) Employer's contribution to state insurance: 5% of (a), (b) and (c) (f) Number of working days in a month: 25 days of 8 hours each (Madras, 1998)
[Ans: labour cost per man-day = Rs 12.57; labour cost per month = Rs 314.42]
- From the following data prepare a statement showing the cost per day 8 hours of engaging a particular type of labourers.
(a) Monthly salary [Basic + DA] Rs200 (b) Leave salary payable to the workers 5% of salary. (c) Employer's contribution to PF 8% of salary [items a and b] (d) Employer's contribution to ESI 2 ½% of salary [items a and b] (e) Pro rata to labour expenditure on amenities Rs17.95 per head per month. (f) Number of working hours in a month 200. [Madras, 1986]
[Ans: labour cost per day = Rs 10; labour cost per month = Rs 250]
Worker's Earnings, Labour cost and their Allocation to Jobs
- Calculate the earnings of workers A and B from the following particulars for a month and allocate the earnings of each to jobs X, Y and Z:
A B (a) Basic wages Rs 100 Rs 100 (b) DA on basic wages 50% 55% (c) PF on basic wages 8% 8% (d) ESI (on basic wages) 2% 2% (e) Overtime 10 hours – (f) Idle time and leave – 16 hours The normal working hours for a month are 200. Overtime is paid at double the normal rate plus DA. Employee's contributions to state insurance and provident fund are at equal rates with the employer's contributions. The month has 25 working days and one paid holiday. The two workers were employed on jobs X, Y and Z in the following proportions:
Overtime was done on job Y.
Madras, 1994]
[Ans: earnings of workers: A—Rs 160, B—Rs 165; labour cost (excluding OT):
A—Rs 160, B—Rs 165; labour costs of jobs: X—Rs 146.5, Y—Rs 96, Z—Rs 97.5]
EXAMINATION PROBLEMS
- Calculate the earnings of workers A and B under straight piece-rate system and Taylor's differential piece-rate system from the following particulars:
Normal rate per hour = Rs 1.80 Standard time per unit = 20 seconds Differentials to be applied: 80% of piece rate below standard 120% of piece rate at or above standard Worker A produces 1,300 units per day and worker B produces 1,500 units per day Ans:
Earnings of worker A:
Low piece rate has been applied because worker A's daily production of 1,300 units is less than the standard daily production of 1,440 units.
Earnings of worker B:
High piece rate has been applied because worker B's daily production of 1,500 units is more than the standard daily production of 1,440 units.
- Calculate the earnings of workers A, B and C under straight piece-rate system and Merrick's multiple piece-rate system from the following particulars:
Normal rate per hour Rs 1.80 Standard time per unit 1 minute Output per day is as follows: Worker A—384 units Worker B—450 units Worker C—552 units Working hours per day are 8 Ans:
Earnings of worker A:
Normal piece rate has been applied because worker A's level of performance is 80%, which is below 83%.
Earning of worker B:
Worker B's level of performance is 93.75%, which is between 83% and 100%; so B is entitled to 110% of normal piece rate (that is, 110% of 3 paise or 3.3 paise per unit).
Earnings of worker C:
Worker C's level of performance is 115%, which is more than 100% of standard output; so C is entitled to 120% of normal piece rate (that is, 120% of 3 paise or 3.6 paise per unit).
- From the following data, calculate the total monthly remuneration of three workers A, B and C under the Gantt's task and bonus scheme:
(a) Standard production per month per worker is 1,000 units (b) Actual production during the month: A—850 units, B—1,000 units and C—1,100 units (c) Piecework rate: 50 paise per unit Ans:
Earnings of worker A:
Worker A's level of performance is 85%, which is below the standard performance; so he will get Rs 500, the guaranteed monthly payment.
Earnings of worker B:
Worker B's level of performance is 100%; so he will get wages for the standard time and a 20% bonus. Thus, his earnings will be as follows:
Rs Wages for 1,000 units at 50 paise per unit 500 Add: 20% bonus 100 600 Earnings of worker C:
Worker C's level of performance is 110%, which is more than the standard performance; so he will get piece wages plus 20% bonus. Thus, his earnings are as follows:

-
Rate per hour = Rs 1.50 per hour Time allowed for job = 20 hours Time taken = 15 hours Calculate the total earnings of the worker under Halsey's plan. Also find the effective rate of earning.
Ans:
Effective rate of earning per hour
Ans:
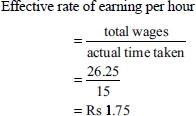
Note: Percentage of bonus is to be taken as 50% when it is not given.
- A worker completes a job in a certain number of hours. The standard time allowed for the job is 10 hours, and the hourly rate of wages is Re 1. The worker earns at the 50% rate a bonus of Rs 2 under Halsey's plan. Ascertain his total wages under the Rowan premium plan.
Ans:
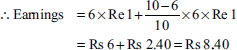
- From the following particulars, you are required to work out the earnings of a worker for a week under (a) straight piece-rate system, (b) differential piece-rate system, (c) Halsey's premium scheme (50% sharing) and (d) Rowan's premium scheme:
Weekly working hours 40 Hourly wage rate Rs 7.50 Piece rate per unit Rs 3.00 Normal time taken per piece 20 minutes Normal output per week 120 pieces Actual output per week 150 pieces Differential piece rate 80% of piece rate when output is below normal and 120% of piece rate when output is above normal Ans:
Particulars Amount (Rs) (a) Straight piece 450 (b) Differential piece rate 540 (c) Halsey's premium scheme 337.50 (d) Rowan's premium scheme 360 - Three workers (Govind, Ram and Shyam), having worked for 8 hours, produced 80, 100 and 120 pieces of a product X, respectively, on a particular day in May in a factory. The time allowed for 10 units of product X is 1 hour and their hourly rate is Rs 4. Calculate for each of the three workers earnings for the day under (a) straight piece-rate, (b) Halsey's premium bonus (50% sharing) and (c) Rowan's premium bonus methods of labour remuneration.
Ans:
- Straight piece-rate system:
Govind = (80 × Re 0.40) = Rs = 32
Ram = (100 × Re 0.40) = Rs 40
Shyam = (120 × Re 0.40) = Rs 48
- Halsey's plan:
Govind = (8 × Rs 4) + (0.50 × nil × Rs 4) = Rs 32
Ram = (8 × Rs 4) + [0.50 × (10 – 8)] × Rs 4 = Rs 36
Shyam = (8 × Rs 4) + [0.50 × (12 – 8) × Rs 4 = Rs 40
- Rowan's plan:
Govind = (8 × Rs 4) + (nil/ 8hours) × 8 hours × Rs 4 = Rs 32
Ram = (8 × Rs 4) + (2 / 10) × 8 hours × Rs 4 = Rs 38.40
Shyam = (8 × Rs 4) + (4/12) × 8 hours × Rs 4 = Rs 42.67
- Straight piece-rate system:
- Standard output per day of 8 hours is 16 units. Actual output of a worker for 8 hours is 20 units. Rate per hour is Rs 2.50. Calculate the wages payable to the worker according to Emerson's efficiency plan.
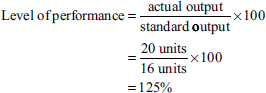
Bonus payable is 45%, calculated as follows:
At 100% efficiency 20% of time wages For the next 25% efficiency at 1% for each 1% increase in efficiency beyond 100% 25% of time wages Total bonus payable 45% of time wages Ans:
Total wages payable 29 - From the following particulars, prepare labour cost per man-day of 8 hours:
(a) Basic salary Rs 2 per day (b) DA 25 paise per every point over 100 (cost of living index for working class); current cost of living index is 700 points (c) Leave salary 10% of (a) and (b) (d) Employer's contribution to PF 8% of (a), (b) and (c) (e) Employer's contribution to state insurance 2.5% of (a), (b) and (c) (f) Expenditure on amenities to labour Rs 20 per head per mensem (g) Number of working days in a month 25 days of 8 hours each Ans:
Total 10.52 - Calculate the normal and overtime wages payable to a worker from the following data:
Days Hours worked Monday 8 hours Tuesday 10 hours Wednesday 9 hours Thursday 11 hours Friday 9 hours Saturday 4 hours Total 51 hours Normal working hours 8 hours per day Normal rate Re 1 per hour Overtime rate Up to 9 hours in a day at single rate and over 9 hours in a day at double rate, or up to 48 hours in a week at single rate and over 48 hours at double rate, whichever is more beneficial to the workers Ans:
irrespective of the method followed, the amount of wages payable to the worker is Rs 54.]
- From the following particulars, prepare a statement of labour cost showing the cost per day (8 hours):
(a) Monthly salary: Rs 4,500 (b) Leave salary: 5% of basic salary (c) Employer's contribution to PF: 8.5% of (a) and (b) (d) Employers contribution to ESI: 3% of (a) and (b) (e) Pro rata experience on amenities to labour: Rs 560 per head per month (f) Number of working hours in a month of 25 days: 8 hours per day Ans:
Labour cost per day (Rs 5,828.38/25) Rs 233.14 - Calculate the normal and overtime wages payable to a worker form the following data:
Days Hours worked Monday 8 Tuesday 10 Wednesday 9 Thursday 11 Friday 9 Saturday 4 Normal working hours are 8 per day, and normal rate is Rs 5 per hour. Overtime rate is up to 9 hours in a day at single rate and at double rate if time exceeds 9 hours, or up to 48 hours (in a 6-day week) at single rate and over 48 hours at double rate, whichever is beneficial to the workers.
Ans:
Rs 270 Note: Both the methods yield the identical sum of wages payable to a worker.
- Computation of wages under various methods of wage payment: In an engineering factory, wages are paid on a weekly basis (48 hours per week) at a guaranteed hourly rate of Rs 3.00. A study revealed that the time required to manufacture a product was 12 minutes. However, a contingency allowance of 25% is to be added to this for normal idle time, setting up time, etc. During the first week of June 1986, X produced 224 pieces. Compute X's wages for the particular week using the following methods of wage payment: (a) time rate, (b) piece rate with a guaranteed time rate, (c) Rowan's premium bonus scheme and (d) Halsey's premium bonus scheme.
Ans:
(a) Attimerate,wages = hours worked × rate per hour = 48 hours × Rs 3 = Rs. 144 (b) X has to be paid Rs 168 as wages. (c) Rowan's scheme = 48 × 3 + (8/56 × 48 × 3) = Rs 144 + 20.57 = Rs 164.57 (d) Halsey's scheme Earnings = hours worked hourly rate + (50/100 × time saved × hourly rate) =48 × 3 + (0.50 × 8 × 3) = Rs 144 + 12 = Rs 156 - Calculation of earnings of workers and their allocation to jobs: Calculate the earnings of A and B from the following particulars for a month and allocate the labour cost to each job X, Y and Z:
A B (a) Basic wages Rs 100 Rs 160 (b) DA 50% 50% (c) Contribution to PF (on basic wages) 8% 8% (d) Contribution to ESI (on basic wages) 2% 2% (e) Overtime (hours) 10 The normal working hours for the month are 200. Overtime is paid at double the total of normal wages and DA. Employer's contributions to state insurance and PF are at equal rates with employees’ contributions. The two workers were employed on jobs X, Y and Z in the following proportions:

Overtime was done on job Y.
Ans:

- Labour hourly rate: Calculate the labour hour rate of a worker P from the following data:
Basic pay Rs 200 per month DA Rs 150 per month Fringe benefits Rs 100 per month Number of working days in a year is 300. Thirty days full-pay leave and 20 days half-pay leave in a year is availed and allowed. Assume 8-hour days. What would be the effect on hourly rate if only 30 days full-pay leave is allowed?
Ans:
Effective working days 270 Effective working hours 2,160 Total wages payable Rs 5,400 Hourly rate Rs 2.50 Effect on hourly rate = Rs 2.61 − Rs 2.50 = Re 0.11 - Calculate the amount of wages and bonus for a worker from the following particulars:
Job commenced: Monday, 24 December 1994 at 8 a.m. Job finished: Saturday, 29 December 1994 at 1 p.m. Quantity of work turned out: 638 Quantity of pieces passed: 600 Worker's rate: Rs 5.00 per hour Time allowed: 10 pieces per hour Bonus: 40% of time saved Assume that the employee worked for 9 hours a day and there is no overtime. Ans:
Total earnings Rs 270 - What will be the earnings of a worker at Rs 5.50 per hour when he takes 140 hours to do a volume of work for which the standard time allowed is 200 hours? The plan of bonus is on sliding scale as under:
Bonus within the first 10% of saving in standard time 40% of time saved Bonus within the second 10% of saving in standard time 50% of time saved Bonus within the third 40% of saving in standard time 50% of time saved Bonus within the fourth 10% of saving in standard time 70% of time saved Bonus for the rest 75% of the time saved Ans:
Total earnings Rs 963.05 - Calculate the earnings of workers A, B and C under Merrick's multiple piece-rate system from the following particulars:
Normal rate per hour Rs 15 Standard time per unit 2 minutes Output per day is as follows: Worker A: 195 units Worker B: 232 units Worker C: 250 units Working hours per day are 8 Solution:
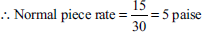
Calculation of level of performance:

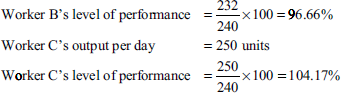
Ans:
Earnings of worker A:
Normal piece rate has been applied because worker A's level of performance is 81.25%, which is lower than 83%.
Earnings of worker B:
Worker B's level of performance is 96.66%, which is between 83% and 100%; so B is entitled to 110% of normal piece rate (that is, 110% of 3 paise or 3.3 paise per unit).
Earnings of worker C:
Worker C's level of performance is 104.17%, which is more than 100% of standard output; so C is entitled to 120% of normal piece rate (that is, 120% of 3 paise or 3.6 paise per unit).
