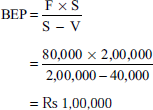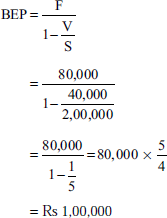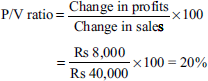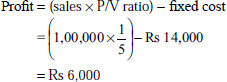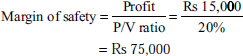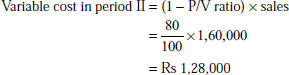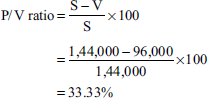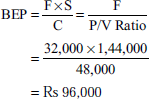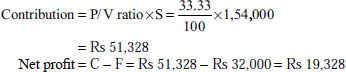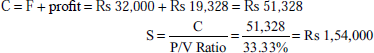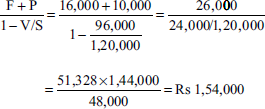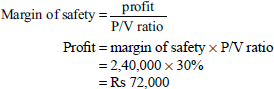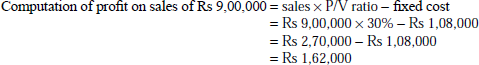13

Marginal Costing

CHAPTER OUTLINE
LEARNING OBJECTIVES

After reading this chapter, you should be able to understand:

  • Meaning of marginal cost and marginal costing
  • Features of marginal costing
  • Limitations of marginal costing
  • Application part of marginal costing
  • Concept of break-even point (BEP)
13.1 INTRODUCTION

Marginal costing is basically concerned with the determination of product cost, which consists of total costs minus fixed costs, for example, direct material, direct labour, direct expenses and variable overheads. In marginal costing, costs are separated into fixed and variable components and only variable costs are included. Marginal costing is not a system of costing but a technique used by managements for decision making. Thus, marginal costing is the same as variable costing. The other names for marginal costing are direct costing, variable costing, differential costing and incremental costing.

The meaning of marginal costing is explained as follows: Marginal costing may be defined as the technique of presenting cost data in which variable costs and fixed costs are shown separately for managerial decision making. Marginal costing is a technique of cost accounting that pays special attention to the behaviour of costs with changes in the volume of output. Marginal costing is a technique of determining the amount of change in aggregate costs due to an increase of one unit over the existing level of production. Thus,

Marginal cost = prime cost + total variable overheads

Marginal cost = total cost − fixed cost

              image

13.2 FEATURES OF MARGINAL COSTING

The features of marginal costing are as follows:

  1. Marginal costing is only a technique.
  2. Fixed and variable costs are kept separate.
  3. Semi-variable costs are also separated into fixed and variable costs.
  4. Only variable costs are considered the cost of the product.
  5. Fixed costs are charged to profit and loss account and are not carried forward to the next year.

  6. Fixed costs remain constant irrespective of the level of activity.
  7. Sales price and variable cost per unit remain the same.
  8. Marginal costs in the long run are stable.
13.3 LIMITATIONS OF MARGINAL COSTING

The limitations of marginal costing are as follows:

  1. Separation of costs into fixed and variable costs is difficult.
  2. It is not correct to say that fixed costs are uncontrollable.
  3. It is not correct to assume that sales price at all levels remains the same.
  4. Where the value of work-in-progress is high, fixation of selling price is difficult.
  5. Marginal costing does not explain the reason for changes that take place in production or sales.
13.4 TWO UNDERLYING PRINCIPLES IN MARGINAL COSTING

The concept of marginal costing can be understood by the following principles:

  1. If the volume of output increases, the cost per unit in normal circumstances reduces.
  2. If the volume of output decreases, the cost per unit in normal circumstances increases.
13.5 BASIC TERMS USED IN MARGINAL COSTING

The basic terms used in marginal costing are as follows:

  1. Fixed costs: ‘Those costs which do not normally change up to the full capacity of firm.’ ‘Those costs which are incurred irrespective of the actual activity.’ ‘Those costs which are fixed in total but variable per unit.’
  2. Variable costs: ‘Those costs which vary in direct proportion to the output or sales.’ ‘Those costs which vary in total but remain constant per unit.’
  3. Semi-variable costs/semi-fixed expenses: Semi-variable costs refer to those expenses that do not change within the limits of a small range of activity but may change when the output reaches a new level. Such an increase or a decrease in expenses is not in proportion to the output.
  4. Contribution: It is the difference between sales and variable costs.

    C = S – V or C = FC + P or C – FC = P or C = S × P/V ratio

    where

    S = sales

    V = variable cost

    FC = fixed cost

    P = profit

    C = contribution

  5. Break-even point: It is the point at which there is neither profit nor loss. In other words, it is at this point that the contribution is equal to fixed expenses.
  6. Margin of safety: It is the difference between total sales and the sales at BEP. It can be expressed in percentage as well as in value. The size of the margin of safety shows the strength of a business. Larger the margin of safety stronger is the business, and vice versa.

    The margin of safety can be increased by the following steps:

    1. Reducing fixed or variable costs
    2. Increasing production
    3. Increasing selling price
    4. Substituting unprofitable production with profitable one
    5. Dropping unprofitable products
  7. Profit/Volume (P/V) ratio: The P/V ratio is the relationship between contribution and sales value. It is expressed as a percentage value. The P/V ratio is considered to be an indication of the profitability of a business. An improvement in P/V ratio leads to an improvement in profitability. The P/V ratio can be improved by
    1. Reducing variable costs
    2. Increasing the selling price
    3. Increasing the output of units having a higher P/V ratio
  8. Key factor/limiting factor: Key factor is ‘the factor in the activities of an undertaking which at a particular point of time or over a period will limit the volume of output’. Thus the key factor or scarce factor puts a limit on production and profitability of an enterprise. In practice, for various reasons there may be limitations to the manufacture of the most remunerative product. For example, although an enterprise may have an order on hand, ample labour and production capacity, it may be unable to get all the required quantities of material over a period for the production of maximum quantities that could be sold. It is a factor that at a particular time or over a period of time limits the activities of an undertaking. Examples of key factors are
    1. Shortage of raw material
    2. Shortage of labour
    3. Plant capacity
    4. Sales capacity
    5. Cash availability
  9. Angle of incidence: This is the angle at which the total sales line cuts the total cost line.
13.6 IMPORTANT FORMULAE USED IN MARGINAL COSTING

Some important formulae used in marginal costing are as follows:

  1. Contribution = sales − variable costs (C = S − V)

                = Fixed costs + Profit (C = F + P)

                = sales × P/V ratio (C = S × P/V ratio)

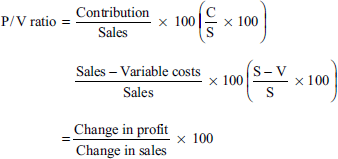
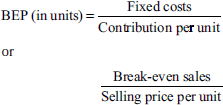
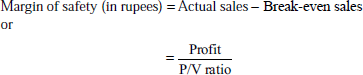
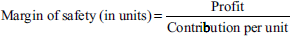
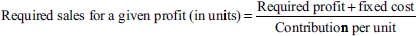
  2. image

  3. image

  4. image

  5. image

  6. image

  7. image

  8. image

Contribution

Illustration 1

From the following information, find the amount of profit earned during the year using marginal cost technique:

 

Fixed cost = Rs 5,20,000

Variable costs = Rs 12 per unit

Selling price = Rs 16 per unit

Output level = 1,50,000 units

(B.Com., Calicut)

Solution:

 

Contribution = Selling price − Marginal cost

                   = Rs 24,00,000 − Rs 18,00,000

                   = Rs (1,50,000 × 16) − Rs (1,50,000 × 12)

                   = Rs 6,00

Contribution = fixed cost + profit

                   = Rs 6,00,000 = Rs 5,20,000 + profit

                   = Rs 6,00,000 − Rs 5,20,000 = profit

          Profit = Rs 80,000

This equation is known as ‘marginal cost equation’. If three factors of the equation are known, it is easy to find the fourth factor. This equation is useful for ascertaining the BEP, P/V ratio and margin of safety.

Break-Even Analysis

Illustration 2

From the following particulars, calculate the BEP:

 

Variable cost per unit = Rs 14

Fixed expenses = Rs 75,000

Selling price per unit = Rs 20

(B.Com., Calicut)

Solution:

                                                   BEP (in units) =image

(Selling price − variable costs = contribution)

(Rs 20 − Rs 14 = Rs 6)

Rs 75,000 ÷ Rs 6 = 12,500 units

BEP (sales) = 12,500 × Rs 20 = Rs 2,50,000

Calculate BEP from the following particulars:

Rs
Fixed expenses 1,50,000
Variable cost per unit 10
Selling price per unit 15

 

(Madras, 1997)

[Ans: BEP = 30,000 units or Rs 4,50,000]

Illustration 3:

You are required to calculate the BEP in the following case: The fixed cost for the year is Rs 90,000; variable cost per unit for the single product being made is Rs 6. Estimated sales for the period are valued at Rs 2,00,000. The number of units involved coincides with the expected volume of output. Each unit sells at Rs 22. Calculate BEP by applying relevant formulae.

 

(C.A. Final)

Solution:

 

Per unit (Rs) Total (Rs)
Sales 22 2,00,000
Variable costs 6 40,000
Contribution 16 1,60,000
Fixed costs 80,000
Profit 80,000

 

  1. Sales at BEP:

     

    image

     

    or

     

    image

     

    or

     

    image

     

    We have to find the P/V ratio:

     

    image

     

  2. BEP in units

    1. image

    2. image

    3. image

Illustration 4

A company estimates that in the coming year it will earn a profit of Rs 50,000. The budgeted fixed costs and sales are Rs 2,75,000 and Rs 10,25,000, respectively. Find the BEP for

 

Solution:

 

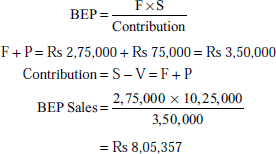
image

 

Illustration 5

From the following data, calculate BEP expressed in terms of units and also the new BEP if selling price is reduced by 10%.

Fixed expenses:

Rs
Depreciation 1,20,000
Salaries 1,30,000
Variable expenses:
    Materials Rs 6 per unit
    Labour Rs 4 per unit
    Selling price Rs 20 per unit

(B.Com., [Pass] Delhi)

Solution:

 

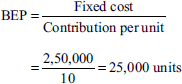
image

 

When the selling price is reduced by 10%, it becomes Rs 20 − Rs 2 = Rs 18 per unit. So, contribution = Rs 18 − Rs 10 = Rs 8.

 

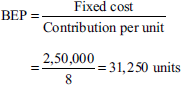
image

 

Illustration 6

Calculate BEP from the following:

Sales = 1,000 units at Rs 20 each = Rs 20,000

Variable costs = Rs 12 per unit

Fixed costs = Rs 16,000

If the selling price is reduced to Rs 18, what is the new BEP?

(Madras, 1987)

Solution:

  1. Contribution per unit = selling price per unit − variable cost per unit

                                     = Rs 20 − Rs 12 = Rs 8

     

    image

     

  2. New selling price = Rs 18
  3. New contribution = Rs 18 − Rs 12 = Rs 6

     

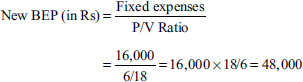
    image

     

     

    image

     

Illustration 7

A company is considering expansion. Fixed costs amount to Rs 4,50,000 and are expected to increase by Rs 1,25,000 when plant expansion is completed. The present plant capacity is 80,000 units a year. Capacity will increase by 50% with the expansion. Variable costs, currently Rs 6.80 per unit, are expected to go down by Re 0.40 per unit with the expansion. The current selling price is Rs 20 per unit and it is expected to remain the same under each alternative. What are the BEPs under each alternative? Which alternative is better and why?

 

(Madras, 1989)

Solution:

  1. Current BEP

    Present capacity = 80,000 units a year

    Contribution = selling price per unit − variable cost per unit

                      = Rs 20 − Rs 6.8 = Rs 13.2

                    image

  2. BEP after expansion:

    Expanded capacity = 1,20,000 units

    New variable cost = Rs 6.80 − Rs 0.40 = Rs 6.40

    New fixed cost = Rs 4,50,000 + Rs 1,25,000 = Rs 5,75,000

    Contribution = 20.0 − 6.40 = 13.6

     

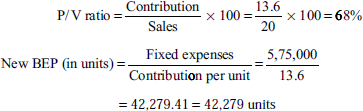
                 image

     

                  image

    Conclusion:

    Current position Position after expansion
    Total contribution 80,000 × 13.2 1,20,000 × 13.6
    Installed capacity Rs 10,56,000 Rs 16,32,000
    Less: fixed cost Rs 4,50,000 Rs 5,75,000
    Profit at full capacity Rs 6,06,000 Rs 10,57,000

    After expansion, the P/V ratio has improved from 66% to 68%. If selling is not a problem, profit can be almost doubled as a result of the increased capacity. The alternative to expand is definitely better due to the improved P/V ratio and scope for higher profits.

Illustration 8

Raviraj Ltd manufactures and sells four types of products under the brand names of A, B, C and D. The sales mix in value comprises 33⅓% , 41⅔%, 16⅔% and 8⅓% of products A, B, C and D, respectively. The total budgeted sales (100%) are Rs 60,000 per month.

Operating costs are

Variable costs:

Product A: 60% of selling price
B: 68% of selling price
C: 80% of selling price
D: 40% of selling price

Fixed cost: Rs 17,500 per month

Calculate BEP for the products on an overall basis and also the break-even sales of individual products. Provide proof for your answer.

(Madras, 1989)

Solution:

P/V ratio for individual products = 100 − percentage of variable cost to sales

 

A = 40% (100 − 60)

B = 32% (100 − 68)

C =20% (100 − 80)

D = 60% (100 − 40)

Calculation of composite P/V ratio:

 

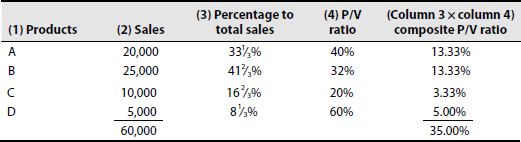
image

 

(After adjusting fractions)

Composite BEP in rupees = image

                                    image

Proof of validity of composite BEP:

Break-even sales Contribution
A: Rs 50,000 × 33⅓% = Rs 16,665 16,665 × 40% = Rs 6,666
B: Rs 50,000 × 41⅔% = Rs 20,830 20,830 × 32% = Rs 6,666
C: Rs 50,000 × 16⅔% = Rs 8,385 8,385 × 20% = Rs 1,668
D: Rs 50,000 × 8⅓% = Rs 4,165 4,165 × 60% = Rs 2,500
Total contribution = Rs 17,500
Total fixed cost = Rs 17,500
Profit/loss = nil

Illustration 9

The sales turnover and profits during two periods are as follows:

 

Period I: Sales = Rs 20,00,000 and profit = Rs 2,00,000

Period II: Sales = Rs 35,00,000 and profit = Rs 5,00,000

(B.Com., Osmania)

Solution:

 

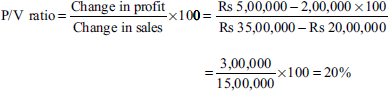
            image

Illustration 10

Calculate the P/V ratio from the following information:

  1. Given: Selling price = Rs 10 per unit and variable cost per unit = Rs 6
  2. Given the profits and sales of two periods as folllows:
    Sales (Rs) Profits (Rs)
    1997 1,50,000 20,000
    1998 1,80,000 30,000

 

Solution:

 

  1. P/V ratio =image

                                                        = 40%

    Contribution = SP – VC, that is, Rs 10 – Rs 6 = Rs 4

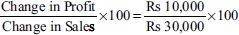
  2. P/V ratio =image

                                                               = 33.33%

Illustration 11

Determine the amount of fixed expenses from the following particulars:

 

Sales = Rs 2,60,000

Direct materials = Rs 82,000

Direct labour = Rs 53,000

Variable overheads = Rs 20,000

Profit = Rs 50,000

 

Solution: The marginal cost equation is

                                                     S – V = F + P

S or sales = Rs 2,60,000

                    V or variable costs = Rs 82,000 + Rs 53,000 + Rs 20,000 = Rs 1,55,000

(V = direct materials + direct labour + variable overheads)

P or profit = Rs 50,000

F or fixed expenses =? (not given)

Applying the figures in the equation S –V = F + P, we get

                                                 Rs 2,60,000 – Rs 1,55,000 = F + Rs 50,000

or

                                                 Rs 2,60,000 – Rs 1,55,000 – Rs 55,000 = F

or

                                                                  Rs 55,000 = F

                                                       ∴ Fixed expenses = Rs 55,000

Illustration 12

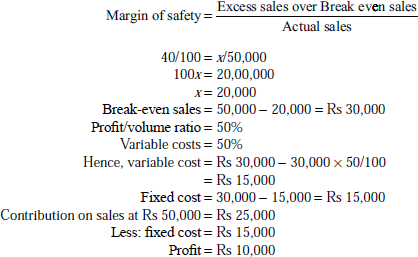
From the following details, find out (a) P/V ratio, (b) BEP and (c) margin of safety:

Rs
Sales 1,20,000
Total costs 70,000
Fixed costs 20,000
Net profit 30,000

Solution:

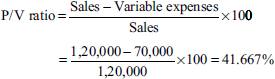
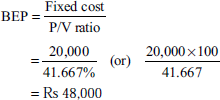
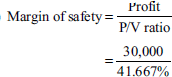
  1. image

  2. image

  3. image

    or

                              image

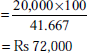
    or

    margin of safety = actual sales -sales at BEP

                            = Rs 1,20,000 – Rs 48,000 = Rs 72,000

Illustration 13

From the following information, calculate

  1. BEP

  2. Number of units that must be sold to earn a profit of Rs 66,000 per year

  3. Number of units that must be sold to earn a net income of 10% on sales

    Sales price = Rs 20 per unit

    Variable costs = Rs 14 per unit

    Fixed costs = Rs 81,000

(Madras, 1989)

Solution:

Contribution per unit = sales price per unit – variable cost per unit

                                = 20 – 14 = 6

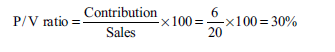
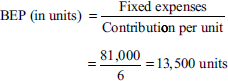
                                   image

  1. image

                     image

  2. Number of units to be sold to make a profit of Rs 66,000 per year:

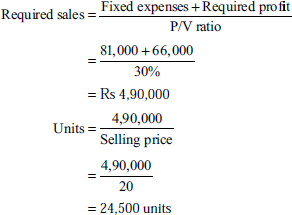
                                image

  3. Number of units to be sold to make a net income of 10% on sales:

    If x is the number of units,

    20x = Fixed costs + variable costs + profit

    20x = 81,000 + 14x + 2x

    20x – 16x = 81,000

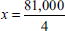
                                                    image

                                                                     = 20,250 units

    Proof: Sales = 20,250 × 20 = Rs 4,05,000

    Less: variable costs = 20,250 × 14 = Rs 2,83,500

    Contribution = Rs 1,21,500

    Less: fixed costs = Rs 81,000

    Profit = Rs 40,500

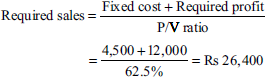
                    Profit as a percentage of sales = image

Illustration 14

From the following information relating to Palani Bros. Ltd, you are required to find out (a) P/V ratio, (b) BEP, (c) profit, (d) margin of safety and (e) volume of sales to earn a profit of Rs 12,000

Rs
Total fixed costs 4,500
Total variable cost 7,500
Total sales 20,000

(Madras, 1995)

Solution: Marginal cost and contribution statemen

Particulars Amount (Rs)
Sales 20,000
Less: variable cost 7,500
Contribution 12,500
Less: fixed cost 4,500
Profit 8,000

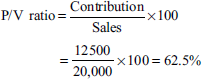
  1. image

  2. image

  3. Profit = Rs 8,000

  4. Margin of safety = sales – break-even sales

                         = Rs 20,000 – Rs 7,200 = Rs 12,800

  5. Sales to earn a profit of Rs 12,000:

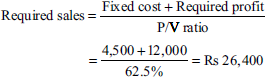
                             image

Illustration 15

From the following data, calculate (a) P/V ratio, (b) variable cost and (c) profit

Rs
Sales 1,00,000
Fixed expenses 20,000
BEP 50,000

 

Solution:

  1. Calculation of P/V ratio:

     

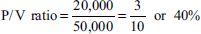
    image

     

     

    image

     

  2. Calculation of variable cost:

    Contribution = sales × P/V

                   image

    Variable cost = sales − contribution

                    = Rs 1,00,000 – Rs 40,000 = Rs 60,000

  3. Calculation of profit:

    Profit = contribution fixed cost

          = Rs 40,000 – Rs 20,000 = Rs 20,000

Illustration 16

Assuming that cost structure and selling prices remain the same in periods I and II, calculate the following: (a) profit volume ratio; (b) fixed cost; (c) BEP for sales; (d) profit when sales are of Rs 1,00,000; (e) sales required to earn a profit of Rs 20,000; (f) margin of safety at a profit of Rs 15,000; and (g) variable cost in period II.

 

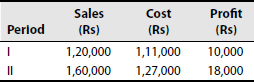
image

 

Solution:

  1. image

  2. image

  3. image

  4. image

  5. image

  6. image

  7. image

Illustration 17

The P/V ratio of a firm dealing in precision instruments is 50% and margin of safety is 35%. You are required to work out BEP and the net profit if the sales volume is Rs 52,00,000. If 25% of variable cost is labour cost, what will be the effect on BEP and profit when labour efficiency decreases by 5%.

(Madras, 1989)

Solution:

Calculation of BEP:

           image

Break-even sales = sales – margin of safety

                           = Rs 52,00,000 – Rs 18,20,000

                           = Rs 33,80,000

Calculation of fixed cost:

 

image

 

Fixed cost = break-even sales × P/V ratio

                  image

Calculation of profit:

    Contribution = sales × P/V ratio

                       = image

Net profit = contribution – fixed cost

               = Rs 26,00,000 – Rs 16,90,000

               = Rs 9,10,000

Effect of decrease in labour efficiency by 5%:

Variable cost = sales – contribution

                     = Rs 52,00,000 – Rs 26,00,000 = Rs 26,00,000

                                   image

 

New labour cost when labour efficiency decreases by 5%

image

Increase in labour cost = Rs 6,84,210 – Rs 6,50,000

= Rs 34,210

∴ New variable cost = Rs 26,00,000 + Rs 34,210

= Rs 26,34,210

Contribution = Rs 52,00,000 – Rs 26,72,222

= Rs 25,65,790

Profit = contribution – fixed cost

         = Rs 25,65,790 – Rs 16,90,000 = Rs 8,75,790

 

image

 

Note: If for 100 units labour cost is Rs 100, 5% decrease in efficiency results in labour producing only 95 units in the same time.

                                                                                                                 ∴ Cost of 95 units = Rs 100

 

image

 

∴ Original labour cost has to be multiplied with image to get the new labour cost.

Illustration 18

Sales turnover and profit during two years are as follows:

Year Sales (Rs) Profit (Rs)
19911,40,00015,000
19921,60,00025,000

Calculate the following:

  1. P/V ratio
  2. BEP
  3. Sales required to earn a profit of Rs 40,000
  4. Fixed expenses
  5. Profit when sales are Rs 1,40,000

          (Madras, B.Com., April 2001 (old); Madras, B.Com., C & M, March 1997; March 1996)

 

Solution: When sales and profit or sales and cost of two periods are given, P/V ratio is obtained by using the ‘change formula’. Fixed cost can be found by ascertaining the contribution of one of the periods given by multiplying sales with the P/V ratio. Then, contribution − profit gives the fixed cost. Ascertaining the P/V ratio using the change formula and finding the fixed cost are the essential requirements in these types of problems.

  1. P/V ratio =image

    Change in profit = Rs 25,000 – Rs 15,000 = Rs 10,000

    Change in sales = Rs 1,60,000 – Rs 1,40,000 = Rs 20,000

     

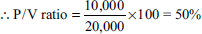
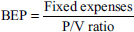
    image

     

  2. image

    Fixed expenses = contribution – profit

    Contribution = sales × P/V ratio

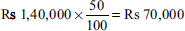
    Using the 1991 sales figure contribution = image

    Fixed expenses = Rs 70,000 − Rs 15,000 = Rs 55,000

    Note: The same fixed cost can be obtained using the 1992 sales figure also.

     

    image

     

  3. Sales required to earn a profit of Rs 40,000:

     

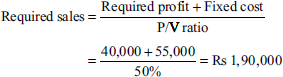
    image

     

  4. Fixed expenses = Rs 55,000 (as already calculated)
  5. Profit when sales are Rs 1,20,000:

    Contribution = sales × P/V ratio

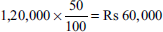
                   = image

    Profit = contribution – fixed cost

         = Rs 60,000 – Rs 55,000

         = Rs 5,000

Illustration 19

A.G. Ltd furnishes the following data related to the year 1996:

First half of the year (Rs) Second half of the year(Rs)
Sales 50,000 60,000
Total cost 40,000 43,000

Assuming that there is no change in prices and variable cost and that fixed expenses are incurred equally in the two half-year periods, calculate the following for the year 1996:

  1. P/V ratio
  2. Fixed expenses
  3. Break-even sales
  4. Percentage of margin of safety

(Madras, 1997)

Solution:

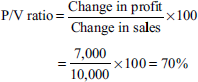
image

 

  1. image

    Contribution = sales × P/V ratio

    During the first half year = Rs 50,000 × 70%

                                     = Rs 35,000

  2. Fixed cost = contribution − profit

    For the first half year = Rs 35,000 − Rs 10,000 = Rs 25,000

    Fixed cost for the full year = Rs 25,000 × 2 = Rs 50,000

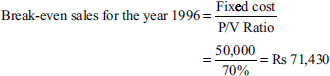
  3. image

  4. Margin of safety for the year 1996:

    Margin of safety = Sales − break-even sales

                         = Rs 1,10,180 − Rs 71,430 = Rs 38,570

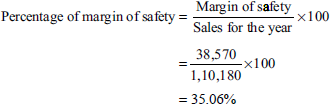
    image

Note:

  1. Since fixed expenses are incurred equally in the two half years, Rs 25,000 is multiplied with 2 to get the fixed cost of the full year.
  2. Sales of both first and second half years are added and the sum is taken as actual sales, that is, Rs 1,10,180, to calculate the margin of safety.

Illustration 20

The following information is obtained from Gopu & Co. for the year ending on 31 March 1998: Sales = Rs 2,80,000; variable costs = Rs 2,10,000; and fixed costs = Rs 30,000. You are required to calculate the following:

  1. Present P/V ratio, BEP and margin of safety
  2. Revised P/V ratio, BEP and margin of safety for each of the following cases:

    1. 25% increase in selling price

    2. 10% decrease in selling price

    3. 20% increase in fixed costs

    4. 10% decrease in fixed costs

    5. 10% increase in variable costs

    6. 10% decrease in variable costs

    7. 10% increase in selling price accompanied by 10% decrease in variable costs

    8. 10% decrease in selling price accompanied by 10% increase in variable costs

Solution: Marginal cost and contribution statemen

Particulars Amount(Rs)
Sales 2,80,000
Less: variable costs 2,10,000
Contribution 70,000
Less: fixed costs 30,000
Profit 40,000

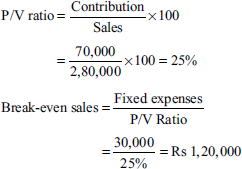
  1. image

    Margin of safety = sales − break-even sales

    = Rs 2,80,000 − Rs 1,20,000 = Rs 1,60,000

  2. Sales showing revised P/V, BEP and margin of safety

     

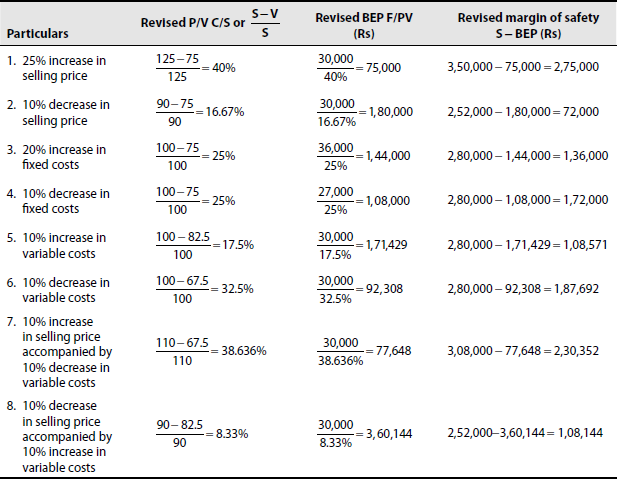
    image

     

Note:

  1. Revised P/V is calculated by making adjustments to the original P/V of 25%, that is, for sales of Rs 100 variable costs is Rs 75 and contribution is Rs 25.

  2. It is assumed that the different changes mentioned do not affect sales volume, that is, number of units of sale, because there is no such indication.

Illustration 21

You are given the following data for the year 1986 for a factory:

 

Output: 60,000 units

Fixed expenses: Rs 2,00,000

Variable cost per unit: Rs 15

Selling price per unit: Rs 30

How many units must be produced and sold in 1987 if it is anticipated that selling price will reduce by 10%, variable cost will be Rs 12 per unit and fixed cost will increase by 10%? The factory wants to make a profit in 1987 that is equal to the profit made in 1986.

(Madras, 1987)

Solution: Marginal cost and contribution statement for the year 1986

Particulars Rs
Sales = 60,000 × 30 18,00,000
Less: variable cost = 60,000 × 15 9,00,000
Contribution 9,00,000
Less: fixed cost 2,00,000
Profit 7,00,000

Calculation of units to be produced and sold in 1987 to make the same profit as in 1986:

 

New selling price = 30 − (30 × 10%) = 30 − 3 = Rs 27

New variable cost = Rs 12 (given)

New fixed cost = 2,00,000 + (2,00,000 × 10%)

                       = 2,00,000 + 20,000 = Rs 2,20,000

 

image

 

Illustration 22

Rs
Present sales 1,50,000
Variable costs 60,000
Fixed costs 30,000

Ascertain the effect of 10% reduction of selling price on P/V ratio and BEP. Also, calculate the sales required to maintain the profit at the present level.

Solution:

  1. Calculation of current P/V ratio and BEP:

     

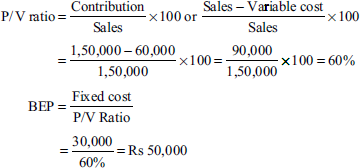
    image

     

  2. Effect of 10% reduction of selling price on P/V ratio and BEP:

    If selling price is reduced by 10% (without any change in sales volume)

    New sales = Rs 1,50,000 − Rs 15,000 = Rs 1,35,000

    Variable costs = Rs 60,000

     

    image

     

  3. Thus, P/V ratio decreases by 6⅔% (from 60% to 55.55%).

     

    image

     

  4. Thus, BEP increases by Rs 4,005 from Rs 50,000 to Rs 54,005.
  5. Sales required to maintain the profit at the present level:

    Present profit = sales − variable costs − fixed costs

                        = Rs 1,50,000 − Rs 60,000 − Rs 30,000 = Rs 60,000

     

    image

     

Illustration 23

From the following information relating to Quick Standard Ltd, you are required to find out

  1. Contribution
  2. BEP in units
  3. Margin of safety
  4. Profit

    Total fixed costs = Rs 4,500

    Total variable costs = Rs 7,500

    Total sales = Rs 15,000

    Units sold = 5,000

     

  5. Also, calculate the volume of sales to earn a profit of Rs 6,000.

(B.Com., ACS)

Solution:

  1. Sales − variable cost = contribution

    Rs 15,500 − Rs 7,500 = Rs 7,500

     

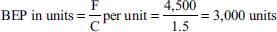
    image

     

  2. image

  3. Margin of safety:

     

    image

     

    Margin of safety = total sales − BEP sales

                         = Rs 15,000 − Rs 9,000 = Rs 6,000

  4. Profit = total sales − total cost

             = Rs 15,000 − (Rs 7,500 + Rs 4,500) = Rs 15,000 − Rs 12,000 = Rs 3,000

  5. Sales to earn a profit of Rs 6,000:

     

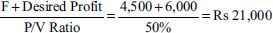
    image

     

Illustration 24

A multipurpose company furnishes the following data for a year:

First half year (Rs) Second half year (Rs)
Sales 45,000 50,000
Total cost 40,000 43,000

Assuming that there is no change in prices and variable costs and that fixed expenses are incurred equally in two half years, calculate the following:

  1. P/V ratio
  2. Fixed expenses
  3. Break-even sales
  4. Percentage of margin of salary

(C.A. Inter)

Solution:

 

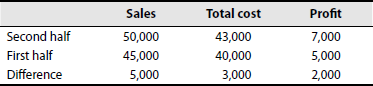
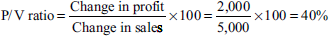
image

 

  1. image

  2. Total sales = Rs 95,000

    Contribution = 40% of Rs 95,000

                   = Rs 38,000

    Less: profit = Rs 12,000

    Fixed cost = Rs 26,000

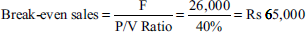
  3. image

  4. Margin of safety = Rs 95,000 − Rs 65,000 = Rs 30,000

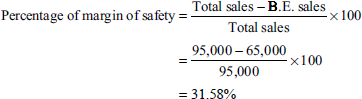
                 image

Illustration 25

You are given the following information regarding a company:

Rs
Fixed cost 13,000
Variable cost 14,000
Total cost 27,000
Net profit 3,000
Net sales 30,000
  1. Find out the BEP.
  2. Forecast the profit for a sales volume of Rs 50,000.
  3. Estimate the volume of sales turnover to make a net profit of Rs 10,000.

(A.C.S. Final)

Solution: Contribution = Rs 30,000 − Rs 14,000 = Rs 16,000

 

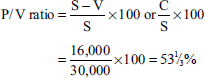
image

 

  1. image

  2. image

  3. image

Illustration 26

In 1994, the position of Y Ltd was as follows:

Rs
Sales 1,44,000
Variable overheads 96,000
Gross profit 48,000
Fixed overhead 32,000
Net profit 16,000

Find out the following:

  1. P/V ratio
  2. BEP
  3. Net profit from the sales of Rs 1,54,000
  4. Required sales for a net profit of Rs 10,000

Solution:

  1. image

  2. image

  3. image

  4. image

    or

     

    image

     

    or

     

    image

     

13.7 APPLICATIONS OF MARGINAL COSTING

13.7.1 Profit planning

Marginal costing helps in profit planning, that is, planning for future operations in such a manner as to maximize profits or to maintain a specified level of profit. Absorption costing fails to bring out the correct effect of change in sales price, variable costs or product mix on the profits of a concern; but this is possible with the help of marginal costing. Profits are increased or decreased as a consequence of fluctuations in selling prices, variable costs and sales quantities in case there is a fixed capacity to produce and sell.

13.7.2 Evaluation of performance of a concern

The different products, departments, markets and sales divisions have different profit-earning potentialities. Marginal cost analysis is very useful for evaluating the performance of the different sectors of a concern. Performance can be evaluated better if distinction is made between fixed and variable expenses. A product, department, market or sales division contributing highly should be preferred over divisions whose contributions are less if fixed expenses remain constant.

13.7.3 Fixation of selling prices

Although prices are controlled more by market conditions and other economic factors than by decisions of management, fixation of selling prices is one of the most important functions of management.

13.7.4 Selection of a suitable product mix

When a factory manufactures more than one product, a problem is faced by management as to which product mix gives the maximum profits. The best product mix is the one that yields the maximum contribution. The products that give the maximum contribution are to be retained and their production must be increased.

The production of products that give comparatively less contribution over others should be reduced or closed down altogether. The effect of sales mix can also be seen by comparing the P/V ratio and BEP. A new sales mix is favourable if it increases the P/V ratio and reduces the BEP.

13.7.5 Maintaining a desired level of profits

Management may be interested in maintaining a desired level of profits. The volume of sales needed to attain a desired level of profit can be ascertained by the marginal costing technique.

13.7.6 Comparing alternative methods of production

Marginal costing is helpful in comparing alternative methods of production, that is, machine work and hand work. The method that gives the greatest contribution (assuming fixed expenses remaining same) is to be adopted keeping, of course, the limiting factor in view. However, where fixed expenses change, decision is taken on the basis of the profit contributed by each method.

13.7.7 Deciding among alternative courses of action

When deciding between alternative courses of action, it shall be kept in mind that whatever the course of action adopted certain fixed expenses remains unaffected. Therefore, the criterion that carries weight is the effect of an alternative course of action upon the marginal (that is, variable) costs in relation to the revenue obtained. The course of action that yields the greatest contribution is the most profitable one to be followed by a management.

13.7.7.1 Key Factor/Limiting Factor

Illustration 27

The following information is given regarding products A and B of a firm:

Product A Product B
Sales priceRs 80Rs 55
Direct materialRs 35Rs 35
Direct labour hours (Re 0.50 per hour)15 hours2 hours
Variable overheads: 100% of direct wages
Fixed overhead: Rs 3,000

Present this information to show the profitability of products during labour shortage.

Solution: Contribution statement

 

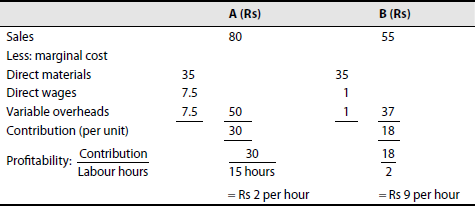
image

 

Therefore, production of product B is more profitable than that of A during labour shortage.

Illustration 28

In a factory producing two different kinds of articles, the limiting factor is the availability of labour. From the following information for the factory for 1994, show which product is more profitable

Product A, cost per unit (Rs) Product B, cost per unit (Rs)
Materials 5.00 5.00
Labour:
   6 hours at 0.50 3.00 1.50
   3 hours at 0.50
Overheads:
   Fixed (50% of labour) 1.50 0.75
   Variable 1.50 1.50
Total cost 11.00 8.75
Selling price 14.00 11.00
Profit 3.00 2.25
Total production for the month 700 units 800 units

Maximum capacity per month = 4,800 hours. Also, give proof in support of your answer.

(B.Com., Madurai)

Solution: Marginal cost statement

 

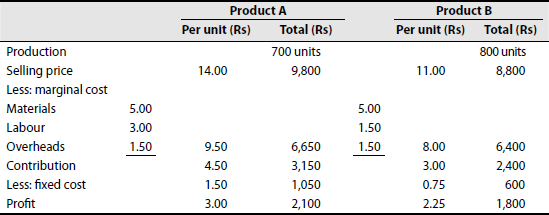
image

 

Contribution per unit of limiting factor:

 

image

 

On the basis of contribution, product A is more profitable. On the basis of net profit also product A is more profitable. On the basis of limiting factor product B is more profitable, as contribution is greater.

Illustration 29

The following particulars are obtained from the records of a company manufacturing two products P and R:

Per unit
Product P (Rs) Product R (Rs)
Selling price250500
Material cost (Rs 20 per kilogram) 40 100
Direct wages (Rs 6 per hour) 60 120
Variable overheads 20 40
Total fixed overhead = Rs 10,000

Comment on the profitability of each product when production capacity in hours is the limiting factor.

(Madras, 1999)

Solution: Statement showing key factor contribution

 

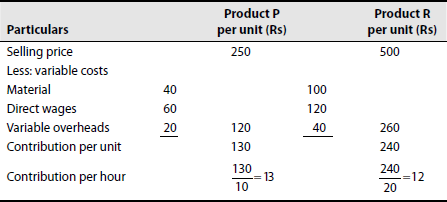
image

 

Note: Hours required to produce the products:image hours image hours

Comment: When production capacity in hours is the limiting factor, the product that gives higher contribution per hour of output is more profitable over others. Product P whose contribution per hour is Rs 8 is better than product R whose contribution per hour is Rs 7. Product P is recommended for production.

In a factory producing two different products, limiting factor is the availability of materials. From the following particulars, which product would you recommend for priority?

Illustration 30

Raman & Co. produces two products X and Y. The technical labour needed to produce the products is in short supply. The following data is available for the year ending on 31 March 2000

Product X per unit (Rs) Product Y per unit (Rs)
Material 40 60
Labour (at Rs 2 per hour) 20 12
Variable overheads (50% of labour) 10 6
Fixed cost (at the current capacity level) 15 30
Selling price 140 180
Units sold 900 2,000

Maximum labour hours available per month = 3,000 hours

If maximum profit is to be attained using the remaining capacity by producing and selling the best product when labour time is limited (present production of either one of the products should be kept as the minimum output), determine the maximum profit.

Solution: Statement showing key factor contribution

 

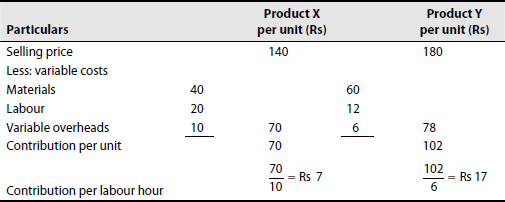
image

 

Note: Labour hours required to produce the products: image hours image hours

When availability of labour hours is the limiting factor, product Y with Rs 17 per hour contribution is more profitable compared to product X with Rs 7 per hour contribution. Therefore, product Y should be produced and sold to the maximum possible extent.

Calculation of optimum production of products X and Y:

 

Maximum labour hours available per annum = 3,000 × 12 = 36,000 hours

Less: Labour hours to be spent for the minimum production required of X = 900 × 17 = 15,300 hours

Labour hours available for the production of Y = 20,700 hours

Number of units of production of image

∴ Most profitable product mix = X (minimum) = 900 units

Y (maximum possible) = 4,500 units

Statement showing estimated contribution and profit per annum

Particulars Rs Rs
Contribution:
Product X900 × 7063,000
Product Y4,500 × 1024,59,000
Total estimated contribution 5,22,000
Less: fixed cost (as per current capacity level)
Product X 900 × 15 = 13,500
Product Y2,000 × 30 = 60,00073,500
Estimated maximum profit 4,48,500

Illustration 31

(This illustration shows fixing of priorities for different products with reference to the key factor.) A company manufactures and markets three products X, Y and Z. All the three products are made using the same set of machines. Production is limited by machine capacity. From the following data, indicate priorities for products X, Y and Z with a view to maximizing profits

 

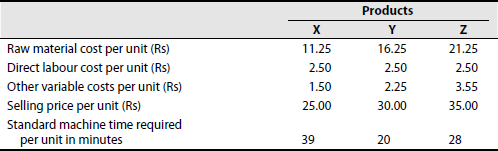
image

 

Solution: Statement indicating priorities of different products to maximize profits

 

image

 

Illustration 32

(This illustration shows the case when different key factors are involved.) The following particulars are extracted from the records of a company:

Per unit
Product A Product B
Sale price (Rs)120130
Consumption of materials (kg)54
Material cost (Rs)2414
Direct wages (Rs)23
Machine hours used23
Variable overheads46

Comment on the profitability of each product (both use the same raw material) when

  1. Total sales potential in units is limited
  2. Total sales potential in value is limited
  3. Raw material is in short supply
  4. Production capacity (in terms of machine hours) is the limiting factor

Solution

Per unit
Product A Product B
Sale priceRs 120Rs 130
Less: variable costsRs 30Rs 23
ContributionRs 90Rs 107
Contribution per rupee of sales (P/V Ratio)0.75 paise0.82 paise
Contribution per kilogram of materialRs 18Rs 26.75
Contribution per machine hourRs 45Rs 35.67
  1. When total sales potential in units is limited, product B is better compared to product A as its contribution per unit is more by Rs 17 (that is, Rs 107 − Rs 90).
  2. When sales potential in value is limited, product B is better compared to product A as its contribution per rupee of sales is more by 0.09 paise (that is, 75 paise − 82 paise).
  3. When raw material is in short supply, product B is better compared to product A as its contribution per kilogram of material is more by Rs 8.75 (that is, Rs 26.75 − Rs 18).
  4. When production capacity (in terms of machine hours) is the limiting factor, product A is better compared to product B as its contribution per machine hour is more by Rs 9.33 (that is, Rs 45 − Rs 35.67).

Make or Buy Decision

Illustration 33

A radio manufacturing company finds that while it costs Rs 6.25 to make each component X 2730, the same is available in the market at Rs 4.85 with an assurance of continued supply. The breakdown of cost is as follows:

Materials Rs 2.75 each
Labour Rs 1.75 each
Other variables Rs 0.50 each
Depreciation and other fixed costs Rs 1.25 each
Rs 6.25 each

Should the company make or buy the component?

(I.C.W.A.)

Solution: The variable cost of manufacturing is Rs 5 (that is, Rs 6.25 − Rs 1.25); but the market price is Rs 4.85. If the fixed cost of Rs 1.25 is also added, it is not profitable to make the component. Because there is a profit of Rs 0.15 even in variable cost, it is profitable to procure the component from outside.

Illustration 34

An automobile manufacturing company finds that the cost of making Part Number 208 in its workshop is Rs 8. The same part is available in the market at Rs 6.60 with an assurance of continuous supply. The cost data to make the part are as follows:

Material Rs 2
Direct labour Rs 3
Other variable costs Re 1
Fixed cost allocated Rs 2
Rs 8
  1. Should the part be made or bought?
  2. Will your answer be different if the market price is Rs 5.60?

Show your calculations clearly.

(Madras, 1987)

Solution: To make a decision regarding whether to make or buy the part, fixed cost is to be ignored as it is irrelevant. But the additional costs being variable costs must be considered

MaterialsRs 2
Direct labourRs 3
Other variable costsRe 1
Total variable costsRs 6
  1. The company should continue to produce the part if the part is available in the market at Rs 6.60 because the production of every part will give the company a contribution of 60 paise (that is, Rs 6.60 − Rs 6.00).

  2. The company should not manufacture the part if it is available in the market at Rs 5.60 because the additional cost of producing the part is 40 paise (Rs 6.00 − Rs 5.60) more than the price at which it is available in the market.

Note: The aforementioned conclusions are made on the assumption that the production facilities that become ‘idle’ once the production of the part is discontinued and the part is bought from the market cannot be used to derive any income. However, if the idle facilities can be leased out or can be used to produce some other product or part that can give some contribution, this should also be considered while making the make or buy decision.

Illustration 35

Green Ltd produces 20,000 units of Part Number 47 every month and uses it in assembling a product. Its cost structure is as follows:

 

Variable cost = Rs 10

Fixed cost = Rs 8

Total cost = Rs18

It is proposed to obtain the part from open market at Rs 15 per unit. It is possible to do one of the following:

  1. Hire out the idle facilities at Rs 35,000 per month
  2. Produce product X using the idle facilities. 5,000 units per month can be produced at a variable cost of Rs 40 each, which can be sold at Rs 55 per unit. Interest on the investment may be ignored.

You are required to advise the management on the aforementioned options and help in arriving at the correct decision—whether to make or buy.

Solution:

  1. Cost of purchase of 20,000 units = Rs 20,000 × 15 = Rs 3,00,000

    Less: Income from hiring idle facilities = Rs 35,000

    Effective cost of outside purchase of Part Number 47 = Rs 2,65,000

    Less: Variable cost of making 20,000 units = 20,000 × 10 = Rs 2,00,000

    Excess cost of outside supply of the part = Rs 65,000

    Conclusion: The part should not be bought. It should be continued to be made in the factory.

     

  2. Sale value of the product to be produced with the use of idle facilities = Rs 5,000 × Rs 55 = Rs 2,75,000

    Less: Variable cost of the product = Rs 5,000 × Rs 40 = Rs 2,00,000

    Net contribution from idle facilities = Rs 75,000

    Cost of purchase of 20,000 units = 20,000 × Rs 15 = Rs 3,00,000

    Less: Income from using idle facilities = Rs 75,000

    Effective cost of outside purchase of Part Number 47 = Rs 2,25,000

    Less: Variable cost of making 20,000 units = 20,000 × Rs 10 = Rs 2,00,000

    Saving in cost by purchasing the part from outside = Rs 25,000

    Conclusion: The part should be bought from outside and the idle facilities should be used.

Note: Since facilities become idle only when outside purchase is made, contribution from idle facilities has to be reduced from the price offered to obtain the effective cost of purchase.

Illustration 36

A manufacturing company finds that while the cost of making a component part is Rs 10, the same is available in the market at Rs 9 with an assurance of continuous supply. Give your suggestions regarding whether to make or buy this part. Also give your views for the case the supplier reduces the price from Rs 9 to Rs 8. The cost information is as follows:

 

Materials = Rs 4

Direct labour = Rs 4

Other variable expenses = Rs 2

Fixed expenses = Rs 2

Total = Rs 12

Solution:

 

Materials = Rs 4

Direct labour = Rs 4

Other variable expenses = Rs 2

Fixed expenses = Rs 2

Total = Rs 12

The company should produce the part if the part is available in the market at Rs 9.00 because the production of every part gives to the company a contribution of 50 paise (that is, Rs 9.00 − Rs 8.50). The company should not manufacture the part if it is available in the market at Rs 8.00 because the additional cost of producing the part is 50 paise (that is, Rs 8.50 − Rs 8.00) more than the price at which it is available in the market. In some cases, in spite of lower variable cost of production there may be an increase in fixed costs. In such cases an increase in fixed cost becomes the relevant cost and it should be considered when making the make or buy decision. It becomes essential to find out the minimum requirement of volume in order to justify the making of a component part over buying it. This volume can be calculated by the following formula =

 

image

 

Illustration 37

A firm can purchase a separate part from an outside source at Rs 11 per unit. There is a proposal that the spare part be produced in the factory itself. For this purpose, a machine costing Rs 1,20,000 with an annual capacity of 20,000 units and a life of 10 years is required. A foreman with a monthly salary of Rs 600 has to be engaged. Materials required are Rs 4 per unit and wages are Rs 2 per unit. Variable overheads are 150% of direct labour. The firm can easily raise funds at 10% per annum. Advise the firm whether the proposal should be accepted.

Solution:

Increase in fixed costs:

 

              image

Contribution per unit:

 

Purchase price = Rs 11

Less: variable cost:

Materials = Rs 4

Wages = Rs 2

Variable overheads = Rs 3

Contribution per unit = Rs 2

 

image

 

In order to accept the proposal, it is essential that the volume is at least 15,600 units. If there is no idle capacity and the making of the spare part in the factory involves the loss of other work, the loss of contribution arising from displacement of work should also be considered along with variable cost of production. The loss of contribution is found with reference to a key or limiting factor. If the purchase price is higher than the total variable cost of production plus traceable fixed costs plus the loss of contribution of production, it will be more profitable to manufacture.

Plant Merger Decision

Illustration 38

The following are the operating details of two plants operating under the same management:

Plant A (Rs) Plant B (Rs)
Sales 12,00,000 10,00,000
Variable costs6,00,0005,00,000
Fixed costs2,00,0001,00,000
Capacity of operation     100%     50%

It is proposed to merge both the plants. You are required to ascertain

  1. Break-even sales and break-even capacity of the merged plant
  2. Profit and profitability of operating the merged plant at 90% of the capacity
  3. Capacity level of operation if a profit of Rs 4,00,000 (the profit made by both the plants before merger) has to be attained by the merged plant

Solution: Statement showing cost and profit of plants A and B before and after merger

 

image

 

Note: It is necessary to merge both the plants at a common capacity level, preferably at 100% capacity.

  1. Break-even sales and break-even capacity of merged plant:

     

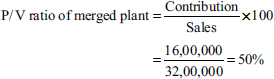
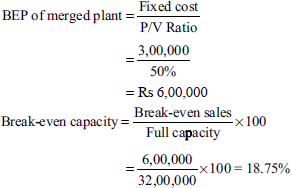
    image

     

     

    image

     

  2. Profit and profitability of operating the merged plant at 90% capacity:

    90% capacity of the merged plant = Rs 32,00,000 × 90% = Rs 28,80,000

    Contribution = sales × P/V

                   = Rs 28,80,000 × 50% = Rs14,40,000

    Profit = contribution − fixed cost

          = Rs 14,40,000 − Rs 3,00,000 = Rs 11,40,000

     

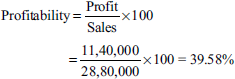
    image

     

  3. Capacity level of operation required to make a profit of Rs 4,00,000:

     

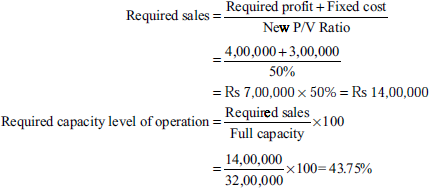
    image

     

Product Mix or Sales Mix

Illustration 39

The budgeted results for Joseph & Co. Ltd include the following

Product Sales (Rs) Variable cost as percentage of sales value
A50,00,00060
B40,00,00050
C80,00,00065
D30,00,00085
E44,00,000 80
2,44,00,00065.77

Fixed overheads for the period is Rs 87,00,000. You are required to

  1. Prepare a statement showing the amount of loss expected
  2. Recommend a change in the sales volume of each product, which will eliminate the expected loss. Assume that the sale of only one product can be increased at a time.

(Madras, 1989)

Solution:

  1. Statement of marginal cost and contribution

     

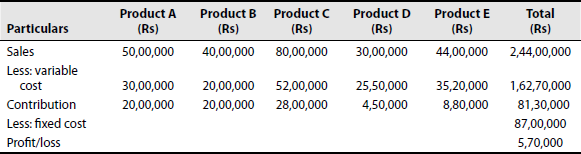
    image

     

  2. Change in the sales volume of each product to eliminate the expected loss:

    P/V ratio of each product = 100 − variable cost percentage given

    ∴ P/V ratio of each product = 100 − 60 = 40%; B = 100 − 50 = 50%

    C = 100 − 65 = 35%; D = 100 − 80% = 20%; E = 100 − 75 = 25%

    Increased sales volume required to get an additional contribution of Rs 5,00,000 and eliminate the current loss:

     

    image

     

    Note: Increase in the sales of any one of the products is enough to eliminate loss.

Illustration 40

Jayant company produces three products A, B and C for which the standard variable costs and standard selling prices are as follows:

 

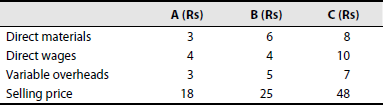
image

 

In two successive periods, the sales are as follows:

 

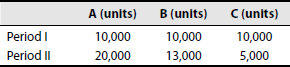
image

 

The fixed overheads amounted to Rs 1,50,000 for each period. In spite of increased sales, the profit for period II has fallen below that of period I. Provide figures to the management to show why this fall in profit should or should not have occurred.

(Madras, 1987)

Solution: Statement showing comparative profit of sales mixes

 

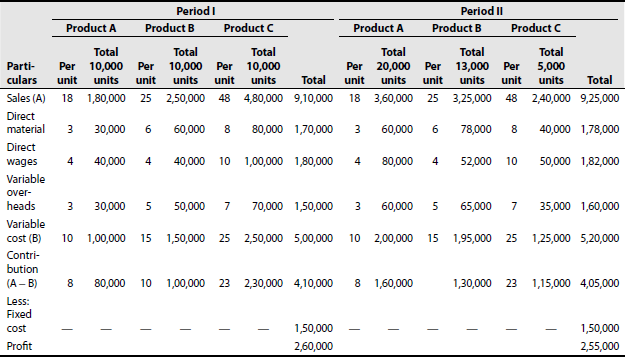
image

 

Contribution per unit: A = Rs 8, B = Rs 10 and C = Rs 23

In period II, the sale of product C, which has the maximum contribution per unit, is reduced by 50% from 10,000 units to 5,000 units. Increase in the sales of products A and B could not fully compensate the decreas in contribution due to decrease in the volume of C. The change of sales mix should not have occurred. The objective should be to increase the sales of products having high contributions.

Illustration 41

Present the following information to show to the management (a) the marginal product cost and the contribution per unit; (b) the total contribution and profits resulting from each of the following sales mixtures

Product A Per unit
Direct materials A Rs 10
B Rs 9
Direct wages A Rs 3
B Rs 2

Fixed expenses are Rs 8,000.

Variable expenses are allocated to products as 100% of direct wages.

Sales price of A = Rs 25

Sales price of B = Rs 20

Sales mixtures:

  1. 1,000 units of product A and 2,000 units of B
  2. 1,500 units of product A and 1,500 units of B
  3. 2,000 units of product A and 1,000 units of B

(M.Com., Madurai)

Solution: Marginal cost statemen

A (Rs) B (Rs)
Direct materials109
Direct wages32
Variable overheads (100%)32
Marginal cost1613
Sales price2520
Contribution97

Product mix choice

 

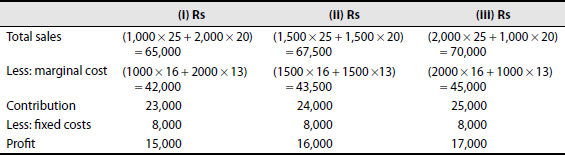
image

 

Therefore, sales mixture (iii) gives the highest profit and, as such, mixture (iii) can be adopted.

Illustration 42

Present the following information to show to the management:

  1. The marginal product cost and the contribution per unit

  2. The total contribution and profits resulting from each of the sales mixtures

  3. The proposed sales mixtures to earn a profit of Rs 250 and Rs 300 with the total sales of A and B being 300 units.

    Product A (Rs) Product B (Rs)
    Direct materials (per unit)109
    Direct wages (per unit)32
    Sales price (per unit)2520

    Fixed expenses = Rs 700

    (Variable expenses are allocated to products as 100% of direct wages.)

    Sales mixtures:

    1. 100 units of product A and 200 units of B
    2. 150 units of product A and 150 units of B
    3. 200 units of product A and 100 units of B

    Recommend which sales mixture should be adopted.

Solution:

  1. Statement of marginal cost and unit contribution

     

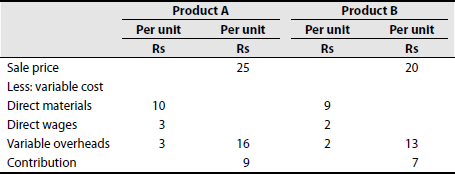
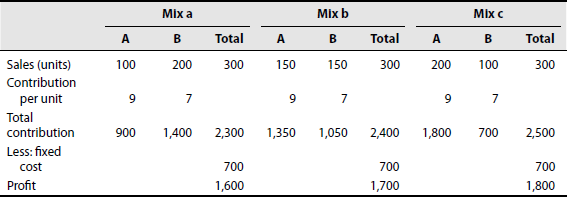
    image

     

    image

     

  2. Mix c should be adopted as it gives the maximum contribution and profit.

  3. Proposed mixes:

    Case I (Rs) Case II (Rs)
    Required profit250300
    Fixed cost700700
    Contribution9501,000

  4. Case I

    Let p numbers of A be sold.

    Then (300 − p) numbers of B are to be sold

    Equating 4p + 2(300 − p) = 950

               4p + 600 − 2p = 950

                                2p = 350

                              ∴ p = 175

    Proposed mix: A = 175units and B = 125 units (that is, 300 − 175)

     

  5. Case II

    Say x numbers of A are to be sold. Then 300 − x numbers of B are to be sold

    Equating, 4x + 2 (300 − x) = 1,000

                  4x + 600 − 2x = 1,000

                                   2x = 400

                                 ∴ x = 200

    Proposed mix: A = 200 units and B = 100 units

Illustration 43

A manufacturer with an overall (interchangeable among the products) capacity of 1,00,000 machine hours has been so far producing a standard mix of 15,000 units of product A and 10,000 units each of products B and C. From experience, the total expenditure exclusive of the manufacturer's fixed charges is found to be Rs 2,09,000 and the cost ratio among the products approximates to 1:1.5:1.75 for A, B and C per unit. The fixed charges come to Rs 2 per unit. When the unit selling prices are Rs 6.25 for A, Rs 7.50 for B and Rs 10.50 for C, the manufacturer incurs a loss. The manufacturer desires to change the product mix as follows:

 

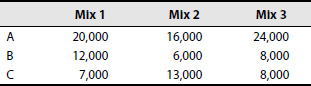
image

 

As a cost accountant what mix do you recommend?

 

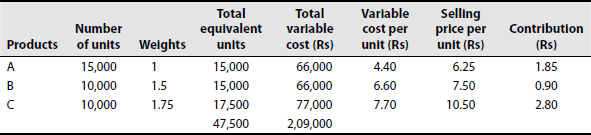
Solution: Calculation of contribution per unit

 

image

 

Statement showing the profitability different mixes

 

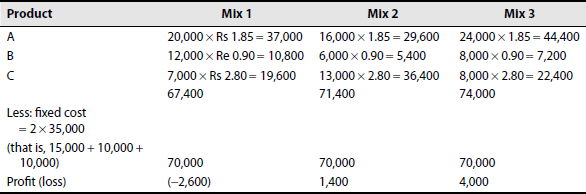
image

 

From the aforementioned data, it is clear that mix 3 is more profitable, and hence it is recommended.

Elimination of a Product or Department

Illustration 44

A company manufactures three products, and their respective details are furnished as follows:

 

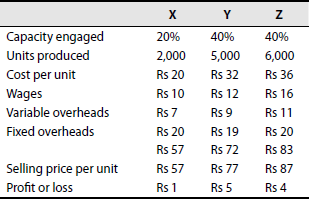
image

 

The management proposes to discontinue line X. It intends to utilize the disengaged capacity in the lines Y and Z equally. Advise the management suitably.

 

(Madras, 1987)

Solution: Statement showing comparative profitability of products X, Y and Z

 

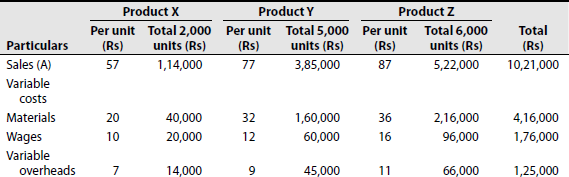
image

 

 

image

 

Working Note: Calculation of fixed cost

X − 2,000 × 20 = 40,000

Y − 5,000 × 19 = 95,000

Z − 6,000 × 20 = 1,20,000

2,55,000

Conclusion:

  1. Product X is the most profitable of the three products because of its higher P/V ratio.
  2. Loss per unit, Rs 2, shown for X is mainly due to the fixed overhead apportioned.
  3. X should not be discontinued. Its sales should be improved if possible.

Illustration 45

The records of Ram Ltd, which has three departments, give the following figures:

 

image

 

The management wants to discontinue department C immediately as it gives the maximum loss. How would you advise the management?

Solution: Marginal cost statement

 

image

 

Here, department A gives negative contribution, and as such it can be given up. Department C has a contribution of Rs 7,000. If department C is closed, then it may lead to further loss. Therefore, C should be continued.

FIXATION OF SELLING PRICE

Illustration 46

The P/V ratio is 60% and marginal cost of the product is Rs 40. What will be the selling price?

Solution:

 

image

 

Illustration 47

From the data given, calculate the following:

  1. P/V ratio
  2. Profit when sales are Rs 30,000
  3. New BEP if selling price is reduced by 25%

Given: Fixed expenses = Rs 4,000

                           BEP = Rs 10,000

(B.Com., Delhi)

Solution:

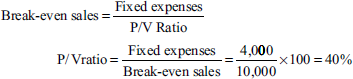
  1. image

  2. When sales are Rs 30,000, the profit is

    = sales × P/V ratio − fixed expenses

    = Rs 30,000 × 40% − 4,000

    = Rs 12,000 − Rs 4,000 = Rs 8,000

  3. If selling price is reduced by 25%, the new BEP is Rs 75 (that is, Rs 100 − Rs 25).

    Variable cost per unit = Rs 100 − 40% = Rs 60

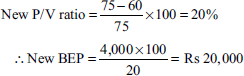
    image

Illustration 48

A company has a P/V ratio of 40%. By what percentage must its sales be increased to offset

  1. 20% reduction in selling price
  2. 25% reduction in selling price

(B.Com., Delhi)

Solution: If sales are 100 units at Re 1 per unit, then

Sales = Rs 100

Contribution = Rs 40

Variable cost = Rs 60

  1. If selling rice is reduced by 20%

    Sales = Rs 80

    Contribution = Rs 20

    Variable cost = Rs 60

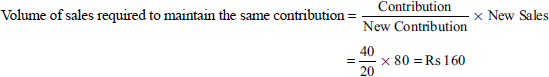
    image

    Thus, if the selling price is reduced by 20%, the volume of sales must be increased by 20%.

     

  2. If selling price is reduced by 60%

    New sales = Rs 75

    New contribution = Rs 15

    Variable cost = Rs 60

image

Thus, if selling price is reduced by 25%, sales must be increased by 100%.

 

Illustration 49

A company produces and sells 100 units of product A per month at Rs 25. Marginal cost per unit is Rs 16 and fixed costs are Rs 3 per month. It is proposed to reduce the selling price by 20%. Find the additional sales required to earn the same profit as before.

(B.Com., Osmania)

Solution:

Present profit:

Selling price of 100 units at Rs 25 = Rs 2,500

Less: marginal cost of 100 units (100 × 12) = Rs 1,200

Contribution = Rs 1,300

Less: fixed cost = Rs 300

Net profit = Rs 1,000

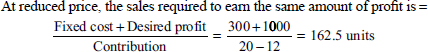
                         image

100 units (sold at present)

100 units (additional)

Additional units = 100

Check:

Sales = Rs 162.5 × Rs 20 = Rs 3,250

Less: variable (162.5 × 12) = Rs 1,950

Contribution = Rs 1,300

Less: fixed cost = Rs 300

Net profit = Rs 1,000

PROFIT PLANNING

Illustration 50

The Delhi Mixers Co. manufactured and sold 1,000 mixies last year at a price of Rs 800 each. The cost structure of a mixy is as follows:

Rs
Materials 200
Labour 100
Variable cost 50
Marginal cost 350
Factory overhead (fixed) 200
Total cost 550
Profit 300
Sales price 850

Due to heavy competition, price must be reduced to Rs 780 in the coming year. Assuming no change in costs, state the number of mixies that would have to be sold at the new price to ensure the same amount of total profits as that of the previous year.

(B.Com.)

Solution:

Profit for 1,000 mixies = 1,000 × 300 = Rs 3,00,000

Contribution at the price of Rs 750 = 750 − 350 = Rs 400

 

image

 

Verification:

 

Sales = 1,250 × Rs 750 = Rs 9,37,500

Less: variable cost = 1,250 × Rs 350 = Rs 4,37,500

= Rs 5,00,000

Less: fixed cost = Rs 2,00,000

Profit = Rs 3,00,000

 

Illustration 51

Two businesses, Y Ltd and Z Ltd, sell the same type of product in the same type of market. Their budgeted profit and loss accounts for the coming year are as follows

 

Y Ltd (Rs) Z Ltd (Rs)
Sales 1,50,000 1,50,000
Less: variable cost 1,20,000 1,00,000
Contribution 30,000 50,000
Less: fixed cost 20,000 40,000
Budgeted net profit 10,000 10,000

You are required to

  1. Calculate the BEP of each business.
  2. Calculate the sales volume at which each business earns Rs 5,000 as profit.
  3. Calculate the sales volume at which both the firms earn equal profits.
  4. State which business is likely to earn a greater profit under the following conditions and briefly give your reasons:
    1. Heavy demand for the product
    2. Low demand for the product

Solution:

 

image

 

(c) image

 

(d) Under conditions of heavy and low demands:

  1. Under conditions of heavy demand, a concern with large P/V ratio can earn high profits because of greater contribution. Thus, Z Ltd is likely to earn greater profit than Y Ltd.
  2. Under conditions of low demand, a concern with low BEP is likely to earn more profit because it will start earning profits at a lower level of sales. In this case, Y Ltd will start earning profits when its sales reach the level of Rs 75,000, whereas Z Ltd will start earning profits when its sales reach the level Rs 1,05,000. Therefore, in the case of low demand BEP should be reached as early as possible so that the concern may start earning profits.
INTRODUCTION OF A NEW PRODUCT

 

Illustration 52

A decision is to be made by the management of a company regarding the possible introduction of a new product. There can be three models of this product, aimed at different sections of the consumer market. The relevant figures are as follows:

 

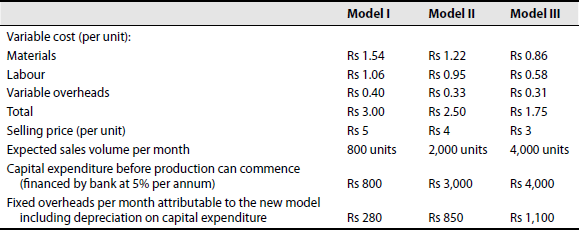
image

 

You are required to prepare a statement of relative profitability and determine for each model the percentage of net profit to selling price at the expected sales volume. Also state, keeping in mind all factors, the production of which model should be commenced by the company?

(M.Com., Agra)

Solution: Profitability Statement

 

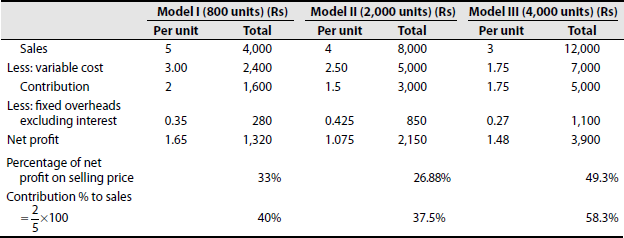
image

 

The management is advised to commence the production of model III, as the contribution percentage is the highest and the percentage of net profit to selling price is satisfactory.

ALTERNATIVE METHOD OF PRODUCTION

 

Illustration 53

The variable cost of the power drill manufactured by Home Tools Limited is Rs 4 and the selling price is Rs 10. The company expects its net profit for the year ending to be Rs 2,75,000 after charging fixed costs amounting to Rs 85,000. The company's production capacity is not fully utilized and market research suggests the following three alternative strategies for the forthcoming year:

 

Strategy Reduce selling price by Sales volume expected to increase by
1 5% 10%
2 7% 20%
3 10% 25%

(a) Assuming the same cost structure as that of the current year, evaluate the alternative strategies available to the company and state the most profitable one.

(CA)

Solution:

 

Rs
Selling price per unit 10
Less: variable cost 4
Contribution per unit 6
Net profit 2,75,000
Add: fixed cost 85,000
Total contribution 3,60,000

Units to be sold = Rs 3,60,000 ÷ Rs 6 = 60,000 units

 

(a) Alternative strategies:

 

image

 

Therefore, strategy 2 is the most profitable one.

 

Illustration 54

Product A can be produced by either machine X or machine Y. Machine X can produce 200 units of A per hour and machine Y 300 units per hour. Total machine hours available during a year are 2,750 hours. Taking into account the following data, determine the most profitable method of manufacture

 

Per unit of product A
Machine X (Rs) Machine Y (Rs)
Marginal cost 10 12
Selling price 18 18
Fixed cost 4 4

(B.Com., Madurai)

Solution:

Machine X Machine Y
Selling price per unit Rs 18 Rs 18
Less: marginal cost Rs 10 Rs 12
Contribution per unit Rs 8 Rs 6
Output per hour Rs 200 Rs 300
Contribution per hour Rs 1,600 Rs 1,800
Machine hour per year 2,750 hours 2,750 hours
Annual contribution Rs 44,00,000 Rs 49,50,000

Therefore, the production of A by machine Y is more profitable.

 

Illustration 55

Product X can be produced by either machine A or machine B. Machine A can produce 100 units of X per hour and machine B 150 units per hour. Total machine hours available during a year are 2,750 hours. Taking into account the following data, determine the most profitable method of manufacture:

Per unit of product X
Machine A (Rs) Machine B (Rs)
Marginal cost 5 6
Selling price 9 9
Fixed cost 2 2

 

Solution: Profitability Statemen

Per unit of product X
Machine A Machine B
Selling price per unit Rs 9 Rs 9
Less: Marginal cost Rs 5 Rs 6
Contribution per unit Rs 4 Rs 3
Output per hour 100 units 150 units
Contribution per hour 400 450
Machine hours per year 2,750 hours 2,750 hours
Annual contribution Rs 11,00,000 Rs 12,37,500

Hence, production by machine B is more profitable.

 

Illustration 56

(Selection of machine) X Limited has been offered a choice to buy either machine A or machine B. You are required to compute

  1. BEP for each of the machines
  2. The level of sales at which both machines earn equal profits
  3. The range of sales at which one machine is more profitable than the other

The relevant data is as follows:

Machines
A B
Annual output (in units) 12,000 12,000
Fixed cost (Rs) 30,000 16,000
Profit above the level of production (Rs) 30,000 24,000

The market price of the product is expected to be Rs 10 per unit.

 

Solution:

 

image

 

  1. As the selling price of the products A and B produced are equal, the machines will earn equal profit when total costs of operation of both the machines are the same.

    If x is the output when total costs of the machines are the same, we have total cost of machine A = 5x + Rs 30,000 and that of machine B = 6.67x + Rs 16,000

    Therefore,

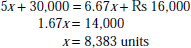
         image

    At a production level of 8,383 units, the profits made by the machines A and B are equal.

  2. The BEP of A is at 6,000 units compared to that of 4,800 units in the case of B and at a production level of 8,383 units A and B earn equal profit. It is quite clear that the profit-earning capacity of machine B is more in the range of 4,000 to 8,383 units as it starts earning profit at lower points. But A will earn more, beyond 7,000 units, as it has a higher P/V ratio, which enables it to earn more incremental contribution on the increasing sales.

 

Illustration 57

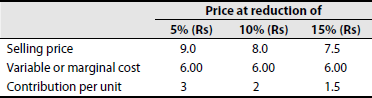
A company produces and markets industrial containers and packing cases. Due to competition, the company aims to reduce the selling price. If the present level of profit is to be maintained, indicate the number of units to be sold for the following proposed reductions in selling price:

 

(a) 10%, (b) 20% and (c) 25%. The following additional information is available:

Rs Rs
Present sales turnover (30,000 units) 3,00,000
Variable cost (30,000 units) 1,80,000
Fixed cost 70,000 2,50,000
Net profit 50,000

 

Solution:

Present price is Rs 10.

 

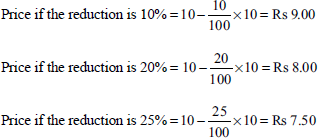
image

 

Contribution at various proposed selling prices:

 

image

 

The contribution required to maintain the present level of profit is as follows:

 

Fixed expenses = Rs 70,000

Profit at present = Rs 50,000

Total = Rs 1,20,000

 

Units to be sold to earn the total contribution of Rs 1,20,000 to maintain the present level of profits:

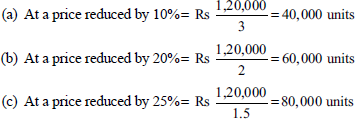
image

ADVANCED SUMS WITH ANSWER

 

  1. From the following information relating to Quick Handcars Ltd, you are required to find out the following:
    1. Contribution,
    2. BEPs in units,
    3. margin of safety and
    4. profit.
    Total fixed costs Rs 2,250
    Total variable costs Rs 3,750
    Total sales Rs 7,500
    Units sold 5,000 units

    Also calculate the volume of sales required to earn a profit of Rs 3,000.

     

    Solution:

    1. Contribution statement
      Total Per unit
      Sales (Rs) 7,500 1.50
      (−) Variable cost (Rs) 3,750 0.75
      Contribution (Rs) 3,750 0

       

    2. BEPs in units:

       

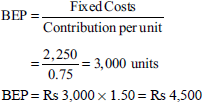
      image

       

    3. Margin of unit:

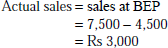
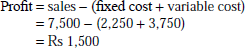
      image

    4. image

    Volume of sales required to earn a profit of Rs 3,000:

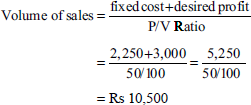
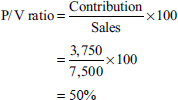
                          image

     

                                   image

     

  2. A company maintains a margin of safety of 37.5% with an overall contribution to sales ratio of 40% in fixed cost amounting to Rs 5,00,000.

    Calculate the following:

    1. Break-even sales
    2. Total sales
    3. Total variable cost
    4. Current profit
    5. New margin of safety if the sales volume is increased by 7 ½%

    Solution:

    1. image

    2. Total sales = break-even sales + margin of safety

      Margin of safety = actual sales − break-even sales

       

      Let actual sales be Rs 100. Margin of safety is Rs 37.50. Hence, break-even sales will be Rs 62.50 in cost. Break-even sales are Rs 62.50 and actual sales are Rs 100.

      Hence, if break-even sales are Rs 12,50,000,

       

      image

       

    3. Contribution = sales − variable costs

      Hence, total variable costs = 60% of Rs 20,00,000

                                                 = Rs 12,00,000

       

    4. image

       

    5. New margin of safety if sales value is increased by 7.5%:

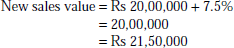
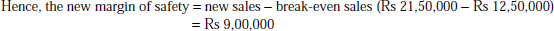
      image

      image

     

  3. The ratio of variable cost to sales is 70%. The BEP occurs at 60% of the capacity sales. Find the capacity sales when fixed costs are sales. Find the capacity sales when fixed costs are Rs 45,000. Also, compute the profit at 75% of capacity sales.

     

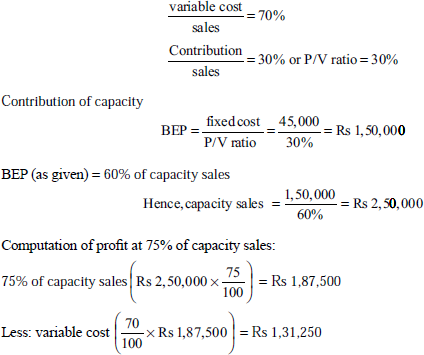
    image

     

    Contribution Rs 56,250
    Less (fixed cost) Rs 45,000
    Profit Rs 11,250

     

  4. The following costs and sales of a manufacturing company for the first and second halves of 2000–01 are given as follows:
    First half Second half
    Sales Rs 24,00,000 Rs 30,00,000
    Total costs Rs 21,80,000 Rs 26,00,000

    You are required to determine

    1. Contribution/sales ratio
    2. Annual fixed costs
    3. BEP
    4. Margin of safety as a percentage of sales

    Solution: Computation of contribution/sales ratio

     

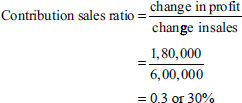
    image

     

     

    image

     

    1. Computation of fixed costs for 2000–01

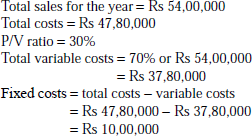
      image

       

    2. image

       

    3. Margin of safety as a percentage of sales

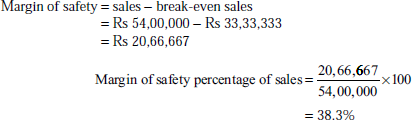
      image

  5. A company earned a profit of Rs 15,000 during the year 1994–95. If the marginal cost and selling price of a product Rs 4 and Rs 5 per unit, respectively. Find out the amount of margin of safety.

    Solution:

     

    image

     

  6. A & Co. has recorded the following data for the two most recent periods
    Total cost of production (Rs) Volume of production
    14,600 800
    19,400 1,200

    What is the best estimate of the fixed costs per period?

    Solution:

     

    image

     

     

    image

     

  7. Y Ltd has earned a contribution of Rs 1,00,000 and a net profit of Rs 75,000 on sales of Rs 4,00,000. What is the margin of safety?

    Solution:

     

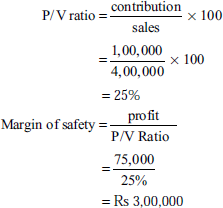
    image

     

  8. From the following data, you are required to calculate BEP and sales value:

    Selling price per unit = Rs 25

    Direct material cost per unit = Rs 8

    Direct labour cost per unit = Rs 5

    Fixed overhead = Rs 24,000

    Variable overhead at 60% on direct labour trade discount 4%.

    If sales are 15% and 20% above the break-even volume, determine the profits.

    Solution: Statement showing BEP of output and sale

    Selling price per unit Rs 25
    (−) Trade discount at 4% 1 24
    (−) Variable cost (Rs):
    Direct material per unit 8
    Direct labour per unit 5
    Variable overheads 3 16
    Contribution per unit 8

     

    image

     

    BEP at sales:

     

    Sales at BEP = 3,000 × 25 = Rs 75,000

    Less: trade discount 4% = Rs 3,000

    Net sales value = Rs 72,000

     

    Statement showing net profit if sales are 15% above the break-even volume

    Units Rs
    Sales at BEP 3,000
    Add: 15% BEP 450
    Total 3,450
    Contribution on 3,450 units (3,450 × 8) 27,600
    Less: fixed cost 24,000
    Profit 3,600

     

    Statement showing net profit if sales are 20% above the break-even volume

    Units Rs
    Sales at BEP 3,000
    Add: 20% BEP 600
    Total 3,600
    Contribution on 3,600 units (3,600 × 8) 28,800
    Less: fixed cost 24,000
    Profit 4,800

     

  9. If the margin of safety is Rs 2,40,000 (40% of sales) and P/V ratio is 30% for AB Ltd, calculate its (i) break-even sales and (ii) amount of profit on sales of Rs 9,00,000.

    Solution:

    1. image

       

      image

       

    2. image
  10. The profit/volume ratio of X Ltd is 50% and the margin of safety is 40%. You are required to calculate the net profit if the sales volume is Rs 50,000.

    Solution:

     

    image

     

CHAPTER SUMMARY

After reading this chapter, one is able to understand the cost concept in marginal costing and its relevance in the decision-making process. It also helps in proper planning in a futuristic business environment.

KEY FORMULAE
  1. Variable overhead per unit = change in the amount of expense/change in activity or quantity
  2. Contribution = sales − variable cost
  3. Contribution = fixed cost + profit
  4. Contribution percentage = P/V ratio percentage
  5. Profit = contribution − fixed cost
  6. Sales − variable cost = fixed cost + profit
  7. P/V ratio = contribution/sales × 100
  8. P/V ratio = change in contribution/change in sales
  9. P/V ratio = change in profit/change in sales
  10. Sales = contribution P/V ratio
  11. Variable cost ratio/marginal cost ratio = 1 − P/V ratio
  12. BEP in value = fixed cost/P/V ratio
  13. BEP in volume = fixed cost/contribution per unit
  14. Sales to earn a desired profit (in value) = fixed cost + desired profit/P/V ratio
  15. Sales to earn a desired profit (in volume) = fixed cost + desired profit/contribution per unit
  16. Margin of safety in value = actual sales − BEP sales
  17. Margin of safety (in value) = profit/P/V ratio
  18. Margin of safety (in volume) = profit/contribution per unit
  19. Margin of safety (in percentage) = margin of safety/actual sales × 100
  20. Sales at a point of loss = fixed cost − loss/P/V ratio
  21. Profit = sales × P/V ratio − (fixed cost)
  22. P/V ratio = profit/margin of safety ratio
EXERCISE FOR YOUR PRACTICE

Objective-type questions

I. State whether the following statements are true or false

  1. In marginal costing, fixed costs are excluded in the valuation of work-in-progress.
  2. In marginal costing, fixed costs are apportioned on some arbitrary basis.
  3. Marginal costing may be used in conjunction with standard costing.
  4. At BEP contribution is equal to fixed cost.
  5. In absorption costing, valuation of stock is higher than that in marginal costing.
  6. In marginal costing, managerial decisions are guided by contribution margin than by profit.
  7. Absorption costing is more suitable for decision making than marginal costing.
  8. Profit in marginal costing is more when production is more than sales.
  9. There is loss in marginal costing when there is production but no sales. 10. Marginal costing is a technique of cost control.

[Ans: 1—true, 2—true, 3—true, 4—true, 5—true, 6—true, 7—false, 8—false, 9—true, 10—true]

II. Choose the correct answer

  1. Marginal costing does not include
    1. Fixed cost
    2. Variable cost
    3. Contribution
    4. Sales

    Ans: (a)

  2. Contribution margin is also known as
    1. Marginal income
    2. Gross profit
    3. Net profit
    4. Loss

    Ans: (a)

  3. Period costs are
    1. Overhead costs
    2. Prime cost
    3. Variable cost
    4. Fixed cost

    Ans: (d)

  4. An increase in variable cost results in
    1. Increase in P/V ratio
    2. Increase in profit
    3. Decrease in contribution
    4. Decrease in profit

    Ans: (c)

  5. A large margin of safety indicates
    1. Overproduction
    2. Overcapitalization
    3. Soundness of business
    4. None of the above

    Ans: (a)

  6. P/V ratio is an indicator of
    1. The rate at which goods are sold
    2. Volume of sales
    3. Volume of profit
    4. Rate of profit

    Ans: (d)

  7. In marginal costing, fixed costs are charged to
    1. Profit and loss account
    2. Income account
    3. Costing profit and loss account
    4. Stores ledger

    Ans: (c)

  8. Margin of safety is the difference between
    1. Planned sales and planned profit
    2. Actual sales and break-even sales
    3. Planned sales and actual sales
    4. None of the above

    Ans: (b)

  9. Contribution =
    1. Fixed cost − loss
    2. Profit + variable cost
    3. Sales − fixed cost − profit
    4. None of the above

    Ans: (a)

  10. In break-even chart, x-axis represents
    1. Sales or volume of production
    2. Profit
    3. Loss
    4. Soundness of business

    Ans: (a)

ADDITIONAL EXERCISES
  1. The details of cost per unit at an activity level of 10,000 units of a product are as follows:
    Rs
    Raw materials 10
    Direct expenses 8
    Labour charges 2
    Variable overheads 4
    Fixed overheads 6
    Total cost per unit 30
    Profit per unit 2
    Selling price per unit 32

    (Madras, B.Com., March 1995)

    [Ans: Break-even quantity—7,500 units; fixed cost—10,000 × 6 = Rs 60,000]

     

  2. From the following data, calculate BEP expressed in terms of units and also the new BEP if selling price is reduced by 10%:
    Fixed expenses:
    Depreciation Rs 1,00,000
    Salaries Rs 1,00,000
    Variable expenses:
    Materials Rs 3 per unit
    Labour Rs 2 per unit
    Selling price Rs 10 per unit

    (B.Com., Delhi)

    [Ans: 40,000 units; 50,000 units if selling price is reduced by 10%]

     

  3. From the following data, find out BEP and break-even sales. If selling price is reduced to Rs 18 per unit, what will be the new BEP and new break-even sales?

    Budgeted output = 1,00,000 units

    Fixed expenses = Rs 5,00,000

    Variable expenses = Rs 10 per unit

    Selling price = Rs 20 per unit

    (Madras, B.A. Corp. C & M (ICE) May 1998)

    [Ans: BEP = 50,000 units; break-even sales = Rs 10,00,000; if selling price is reduced to Rs 18, BEP = 62,500 units; break-even sales = Rs 11,25,000]

     

  4. From the following information, find P/V ratio and margin of safety:
    Rs
    Sales 10,00,000
    Variable cost 4,00,000
    Fixed cost 4,00,000

    (Madras, B.Com., March 1997)

    [Ans: P/V ratio = 0.6 or 60%; margin of safety = Rs 3,33,333]

     

  5. Calculate the BEP from the following:
    1. Sales price = Rs 10 per unit
    2. Variable cost = Rs 6 per unit
    3. Fixed overheads = Rs 20,000

    Calculate the revised BEP if

    1. Sales price is increased to Rs 11 per unit
    2. Sales price is reduced to Rs 9 per unit
    3. Variable cost is increased to Rs 7 per unit
    4. Variable cost is reduced to Rs 5 per unit
    5. Fixed overheads rise to Rs 25,000
    6. Fixed overheads fall to Rs 15,000

    [Ans: (A) 5,000 units. (B) (i) 4,000 units; (ii) 6,667 units; (iii) 6,667 units; (iv) 4,000 units; (v) 6,250 units; (vi) 3,750 units]

     

  6. From the following information find (a) BEP and (b) margin of safety:
    Rs
    Total fixed costs 1,80,000
    Total variable cost 3,00,000
    Selling price is Rs 6 per unit, number of units sold 2,00,000

    (Madras, B.Com., Sep. 1987)

    [Ans: (a) 40,000 units or Rs 2,40,000; (b) 1,60,000 units or Rs 9,60,000]

     

  7. From the following details, find
    1. P/V ratio
    2. Break-even sales
    3. Margin of safety
    Sales Rs 1,00,000
    Total cost Rs 80,000
    Fixed cost Rs 20,000
    Net profit Rs 20,000

    (Madras, B.A. Corp. April 1998)

    [Ans: (a) 4 or 40% (b) Rs 50,000 (c) 50,000]

     

  8. From the following data, calculate (a) BEP (in units). (b) If sales are 10% and 15% above the break-even volume, determine the net profit.

    Selling price per unit = Rs 10

    Direct material per unit = Rs 3

    Fixed overheads = Rs 10,000

    Variable overhead per unit = Rs 2

    Direct labour cost per unit = Rs 2

    (Madras, B.Sc. C & M, Oct. 1998)

    [Ans: (a) 3,333.33 or 3,334 units; (b) profit if sales are 10% above BEP sales = 3,334 + 333.4 or 334 units = 3,668 units; profit = Rs 1,004; profit if sales are 15% above BEP sales = 3,334 + 500 = 3,834 units; profit = Rs 1,502]

  9. From the following information, calculate (a) P/V ratio, (b) BEP and (c) margin of safety:
    Rs
    Total sales 3,60,000
    Selling price per unit 100
    Variable cost per unit 50
    Fixed costs 1,00,000

    If the selling price is reduced to Rs 90, by how much is the margin of safety reduced?

    (Madras, M.Com., April 1994)

    [Ans: (a) 0.5 or 50%; (b) 2,000 units or Rs 2,00,000; (c) current margin of safety = 3,60,000 − 2,00,000 = Rs 1,60,000; new margin of safety = 3,24,000 − 2,25,000 = Rs 99,000; reduction in margin of safety with reduction in selling price = Rs 61,000]

DISCUSSION QUESTIONS
  1. Define marginal costing. Discuss its usefulness.
  2. What is contribution?
  3. Discuss the following terms:
    1. BEP
    2. Margin of safety
    3. Key factor
    4. P/V ratio
  4. What do you understand by the term break-even analysis?
  5. What are the other names of marginal costing?
  6. Discuss the role of contribution in marginal costing.
  7. Distinguish between marginal costing and absorption costing.
  8. How is break-even chart prepared?
  9. What information does the break-even chart give?
  10. What are the different applications of marginal costing?
  11. Distinguish between contribution and profit.
..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
3.22.249.48