Chapter 17
FX Derivatives Market Analysis
Traders analyze the FX derivatives market in order to identify relatively cheap and expensive aspects of the volatility surface. This analysis is then used to position trading books and generate trade ideas for clients. The FX derivatives market has many moving parts and there are a correspondingly large number of ways in which it can be investigated.
Calculating Breakevens
The simplest FX derivatives analysis involves combining a short-dated vanilla option payoff with its premium to calculate its breakeven. Assuming the option is left unhedged until maturity, if spot moves beyond the breakeven point, the trade will make money. This breakeven point can be compared with expectations of spot movement to determine whether the option is cheap or expensive.
For a single vanilla option, the premium (expressed in CCY2 pips) is added onto (for a call option) or taken away from (for a put option) the strike level to determine the breakeven. For example, if current USD/JPY spot is 95.00 and the premium on a 3mth 100.00 USD call/JPY put option is 400 JPY pips, the breakeven on the option is 104.00. This is shown in Exhibit 17.1.
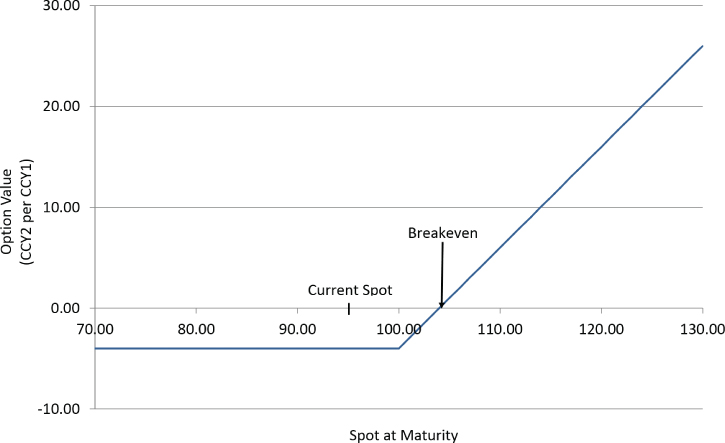
Exhibit 17.1 Call option breakeven
As the strike is moved higher, the premium decreases but the breakeven moves further away, as shown in Exhibit 17.2.

Exhibit 17.2 Call option breakevens
For a short-dated ATM straddle, the breakeven is calculated by summing the call and put premiums. The breakeven is now two-sided and symmetric, as per Exhibit 17.3.

Exhibit 17.3 ATM straddle option breakeven
Typical trader analysis compares the historic range of spot in, for example, the last week versus the breakeven on a 1wk ATM straddle. However, care must be taken because these measures are not directly comparable. For example, spot may well establish a range larger than a 60-pips breakeven, but if it moves, for example, 80 pips up and then 80 pips down, unless the delta has been hedged perfectly (not likely), money will still be lost from buying the straddle. As a rough rule of thumb, spot usually needs to establish a range approximately double the breakeven for positive P&L overall to be generated from buying a short-dated ATM contract.
Breakeven analysis is particularly popular when the expiry date covers a major economic event. The one-day breakeven over the event can be calculated from the forward overnight volatility (i.e., the overnight ATM option expiring after the event). This value can be compared with historic spot moves caused by the event.
Implied versus Realized Analysis
The most popular FX derivatives market analysis compares implied volatility with realized volatility. The central idea is that if implied volatility is higher than realized volatility, vanilla options should be sold and if implied volatility is lower than realized volatility, vanilla options should be bought. This is simple analysis but it can be effective if applied with an understanding of its limitations.
Implied volatility is at the core of the FX derivatives market. Within analysis the ATM implied volatility at a market tenor (e.g., 1mth, 2mth, etc.) is usually used because these reference contracts are directly quoted in the market. Using the implied volatility for another strike (e.g., the forward) or a non-market tenor expiry would require the entire volatility surface to be constructed—additional complication for only minimal benefit.
Realized (historic) spot volatility is calculated from spot samples. The required measure is the annualized volatility of the sample log returns.
Implied volatility and realized volatility are linked but they are not always directly comparable for a number of reasons. First, implied volatility is forward looking; it gives the pricing for option contracts expiring in the future. Realized volatility is backward looking; it is calculated using historic spot samples. This is shown in Exhibit 17.4.
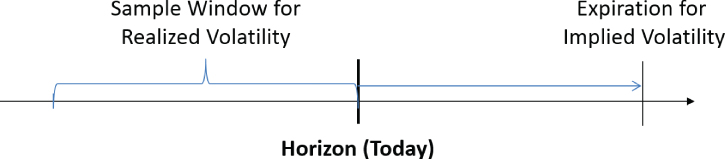
Exhibit 17.4 Realized volatility versus implied volatility
Second, both volatility measures are impacted by events and holidays. Event days (i.e., days on which significant economic data is released) usually have increased volatility and holiday days usually have reduced volatility. Implied volatility and realized volatility are best compared when they mean the same thing; assessing the value in events themselves is another problem.
For example, comparing 1mth ATM implied volatility with 1mth realized volatility in early January will usually show a higher implied volatility because Christmas and New Year's holidays dampen realized volatility. In this case, implied volatility above realized volatility is not a signal that implied volatility is expensive. This situation is shown in Exhibit 17.5.

Exhibit 17.5 Realized volatility versus implied volatility in early January
Therefore, when analyzing volatility at shorter tenors (approximately sub-3mth) the effect of events and holidays should ideally be removed. Core (excluding events) realized volatility can be calculated by removing log returns at or immediately after major events. Core implied volatility can be calculated by removing the additional variance attributed to major events. At longer tenors, event and holiday day effects can be ignored because they will not significantly bias the analysis.
Sample frequency and sample time also significantly impact the realized volatility calculation. Exhibit 17.6 shows one month of market AUD/USD spot trades plus two daily snapshots, one taken at 3 p.m. and the other at 5 p.m. Note the gaps in data over the weekends, the outlier samples in the high-frequency data, and how much information is being ignored if only daily samples are used.

Exhibit 17.6 High-frequency AUD/USD spot trades
Using the data from Exhibit 17.6:
- Realized volatility calculated using 3 p.m. samples = 7.9%
- Realized volatility calculated using 5 p.m. samples = 7.6%
- Realized volatility calculated using minute samples = 10.5%
In general, using a small number of samples causes realized volatility to be biased low.
Using higher frequency samples gives better results up to a point but realized volatility does not necessarily converge as sampling frequency increases. So-called “tick data” contains all spot market activity on a given trading venue but noise in the data can cause realized volatility calculated using a full set of tick data to be biased high. Therefore, tick data is often filtered before being used to calculate realized volatility, or the result is adjusted afterward.
It is important to take into account what the spot samples represent; is it trade data or is the data derived from a market bid and offer? Fundamentally, the point of the calculation is to measure volatility that can be traded, so, for example, if the bid–offer spread widens, that should not result in increased realized volatility.
In general, sample frequency should be aligned with calculation tenor. Using high-frequency data to calculate 5yr realized volatility is unnecessary and using daily data to calculate 1wk realized volatility will not contain enough samples for the result to be meaningful. In general, there is no truly “correct” realized volatility for a given period of market spot action. It is most important to ensure that a sensible and consistent methodology is used throughout the analysis.
Care must also be taken when using implied volatility at longer tenors (past two years) because ATM strike versus forward differences introduce a possible source of error into the analysis.
Example: AUD/JPY ATM versus ATMF (at-the-money-forward) implied volatility:
- AUD/JPY spot: 95.90
- 5yr ATM strike: 73.85
- 5yr ATM implied volatility: 15.35%
- 5yr forward: 78.30 (almost five figures above the ATM strike)
- 5yr ATMF implied volatility: 14.30% (more than 1% below the ATM volatility)
When analyzing longer tenors it is often preferable to use the implied volatility of the forward strike because the positioning of the ATM strike is impacted by market conventions. Alternatively, a convention-free long-term volatility parameter from a volatility surface model or pricing model could be used.
Calculating Realized Spot Volatility
The standard sample realized volatility calculation is:

where N is the number of log returns in the sample, Xi are log returns  , and
, and ![]() is the mean of the Xi. This function can be accessed in Excel using =STDEV or =STDEV.S.
is the mean of the Xi. This function can be accessed in Excel using =STDEV or =STDEV.S.
To calculate the annualized volatility, multiply ![]() by
by ![]() where
where ![]() is the number of samples per year.
is the number of samples per year.
Example: Calculating AUD/USD realized spot volatility using daily samples:
- Get daily sampled spot data (shown in Exhibit 17.7).
- Calculate log returns (shown in Exhibit 17.8).
- Calculate the standard sample realized volatility of the log returns using the above formula.
- Calculate annualized realized volatility. Data is sampled daily so the realized volatility must be multiplied by
 . Going forward, the term realized volatility is taken to mean annualized realized volatility.
. Going forward, the term realized volatility is taken to mean annualized realized volatility.
Exhibit 17.7 AUD/USD daily spot samples

Exhibit 17.8 AUD/USD daily spot log returns
Assessing trends in realized volatility is also important when comparing realized volatility with implied volatility. Set up a rolling calculation window and calculate a realized volatility time series using the samples within the window. In Exhibit 17.9 the realized spot volatility is calculated using a rolling 6mth calculation window.

Exhibit 17.9 AUD/USD 6mth realized spot volatility
Notes on Calculating Realized Spot Volatility
Note 1: The number of trading days in a year in the United States is usually 252, and this is the factor most often used to annualize daily sampled realized volatility whether there are exactly 252 trading days in a given currency or not.
Note 2: It sometimes makes sense to remove the mean term from the realized volatility calculation because it can introduce noise into the calculation, that is,

Tradable volatility depends mainly on spot changes rather than whether the market is trending (hence a larger mean term exists in the calculation). Consider that a spot steadily rising the same amount (in log-space) each day will have zero daily realized volatility when calculated with the standard method. However, that spot action is certainly not equivalent to a static spot within a trading position.
Note 3: To keep things simple, enough data samples should be used to ensure that issues around biased versus unbiased calculations can be ignored. As a very rough rule of thumb, aim for at least 50 data samples within the realized volatility calculation.
Exponentially Weighted Moving Average (EWMA) Volatility
The standard realized volatility calculation does not behave well when there are extreme jumps within the data: Standard realized volatility drops sharply as the jump data point exits the back of the sample window. This feature makes it difficult to compare standard realized volatility with implied volatility when the data contains jumps. A rolling realized volatility calculation that clearly shows the entrance and exit of an extreme jump into the sample window is given in Exhibit 17.10.

Exhibit 17.10 1mth realized volatility with an extreme spot jump
Therefore, Exponentially Weighted Moving Average (EWMA) volatility can be used instead. Within EWMA, weights are attached to each log return in the sample with the most recent samples weighted most highly and weights decreasing exponentially on older samples based on a λ parameter (0 < λ < 1). The weights for historic parameters for different λ parameters are shown in Exhibit 17.11.

Exhibit 17.11 EWMA weights
Higher λ is therefore equivalent to using a larger sample window. A groundbreaking J.P. Morgan RiskMetrics paper from 1996 which is available on the internet shows that using λ = 0.97 is roughly equivalent (1% tolerance) to using 151 samples.
The EWMA calculation builds up over all available samples, not a specific sample window. Therefore, for example, “0.97 EWMA realized volatility” is calculated rather than, for example, “6mth EWMA realized volatility,” although EWMA volatility still needs to be annualized in the same way as standard realized volatility.

Under EWMA, the impact of the extreme spot jump decays away exponentially over time as per Exhibit 17.12.

Exhibit 17.12 0.97 EWMA realized volatility with an extreme spot jump
This measure of realized volatility looks intuitively better, but if the extreme event is truly an outlier, perhaps it would be better to exclude it completely from the analysis. Plus, although the exponential decay function seems reasonable, there is no certainty that it is the right way to model the market “forgetting” extreme events.
Finally, the choice of λ can make a big difference to the output. Once again, there is no “correct” λ, although values between 0.90 and 0.99 are most commonly used in practice. The choice of λ must be made with reference to the sample frequency and the approximate number of samples which should have significance within the EWMA calculation.
Realized Spot Volatility versus Realized Forward Volatility
A European vanilla option has delta exposure (along with all other Greeks) to the option expiry; i.e., a 1yr vanilla option should ideally be delta hedged with a 1yr forward. In practice this means that if delta hedging was performed to the option maturity throughout its life, forward deltas to closer and closer maturities should be traded with each day that passes. This suggests that the realized volatility calculation should be adjusted in a similar manner, using different expiry dates. However, this requires substantial additional calculation for minimal benefit so this adjustment is rarely applied in practice.
However, when analyzing long-dated maturities, the realized volatility of the forward outright to a fixed tenor is often calculated. Realized volatility analysis now becomes two-dimensional; forward tenor and sample window can both be varied.
Example: Calculating AUD/USD realized 5yr forward outright volatility from daily samples. The realized volatility of the forward outright is calculated in the same way as the realized volatility of spot:
- Collect daily sampled 5yr forward outright data (shown in Exhibit 17.13).
- Calculate log returns.
- Calculate annualized volatility based on sample frequency.
- Use a rolling calculation window to generate a time series of implied volatility. In Exhibit 17.14, the spot and 5yr forward outright realized volatility is calculated over a rolling 6mth calculation window.

Exhibit 17.13 AUD/USD daily spot and 5yr forward outright samples

Exhibit 17.14 AUD/USD spot and 5yr forward realized volatility with 6mth rolling calculation window
Realized spot volatility versus realized forward volatility differences are driven by:
- Spot versus interest rate correlation
- Interest rate volatility
Recall that in continuous time space:
And swap points define the difference between spot ![]() and forward to time T
and forward to time T ![]() :
:
This framework is shown in Exhibit 17.15.

Exhibit 17.15 Spot and 5yr forward framework
If CCY1 interest rates fall or CCY2 interest rates rise, swap points go more positive. If spot is static, the forward moves higher as shown in Exhibit 17.16.

Exhibit 17.16 Spot and 5yr forward framework with a higher forward
If CCY1 interest rates rise or CCY2 interest rates fall, swap points go more negative. If spot is static, the forward moves lower as shown in Exhibit 17.17.

Exhibit 17.17 Spot and 5yr forward framework with a lower forward
Therefore:
- Negative correlation between spot and CCY1 interest rates or positive correlation between spot and CCY2 interest rates → as spot moves higher or lower the forward moves more in the same direction → realized forward volatility will be higher than realized spot volatility.
- Positive correlation between spot and CCY1 interest rates or negative correlation between spot and CCY2 interest rates → as spot moves higher or lower the forward moves less in the same direction → realized forward volatility will be lower than realized spot volatility.
Plus, if interest rate volatility is zero, realized forward volatility is equal to realized spot volatility, whereas if interest rates are volatile (with no significant correlation effect), then realized forward volatility will be higher than realized spot volatility.
Calculating Realized Spot versus Interest Rate Correlations
Correlation is a measure of the strength of relationship between two variables. Pearson's coefficient ρ is the standard measure of realized correlation:
where  is the covariance between X and Y,
is the covariance between X and Y, ![]() is the realized volatility of X,
is the realized volatility of X, ![]() is the mean of the Xi, and N is the number of data samples. This function can be accessed in Excel using =CORREL.
is the mean of the Xi, and N is the number of data samples. This function can be accessed in Excel using =CORREL.
Correlation calculated using a small number of samples can be extremely unstable as shown in Exhibit 17.18. As with realized volatility, the calculation window should be linked to the sample frequency; short time-scale correlations should be calculated using high-frequency data plus sample times must be synchronized; that is, both variables should be sampled at exactly the same time.

Exhibit 17.18 AUD/USD versus USD/JPY spot correlation
Example: Calculating spot versus interest rate correlation using daily samples:
- Get daily sampled spot and interest rate data (shown in Exhibit 17.19).

Exhibit 17.19 AUD versus USD 5yr daily deposit rate samples
It is not always straightforward to determine which interest rate data to use within analysis; different interest rate instruments are traded at different maturities. In liquid G10 currency pairs at shorter tenors, OIS, libor, deposits, and futures are traded, whereas at longer tenors, interest rate swaps are often the most liquid instrument. In other currencies, interest rate markets are less liquid than forwards, so, for example, a USD rates curve plus the forward can be used to imply interest rates in the other currency. These issues can usually be ignored within FX derivatives market analysis providing a consistent measure of interest rates is used. Whether the product is a swap, a deposit, or a future becomes inconsequential so long as the rate reacts appropriately as market interest rates change.
In this analysis, full interest rates curves were generated using different instruments; then the “5yr interest rate” is calculated in deposit rate terms, even though that contract is never actually quoted in the market.
- Take log returns or returns as appropriate. For interest rates, since they can go negative, it is arguably better to use returns rather than log returns within the calculation (i.e.,
 where
where  is the ith interest rate sample).
is the ith interest rate sample). - Calculate the correlation between spot log returns and interest rate returns.
- Calculate a realized correlation time series using a rolling sample window.
Exhibit 17.20 shows that within the data there is no strong correlation between AUD interest rates and AUD/USD spot, but a persistent negative correlation between USD interest rates and AUD/USD spot.
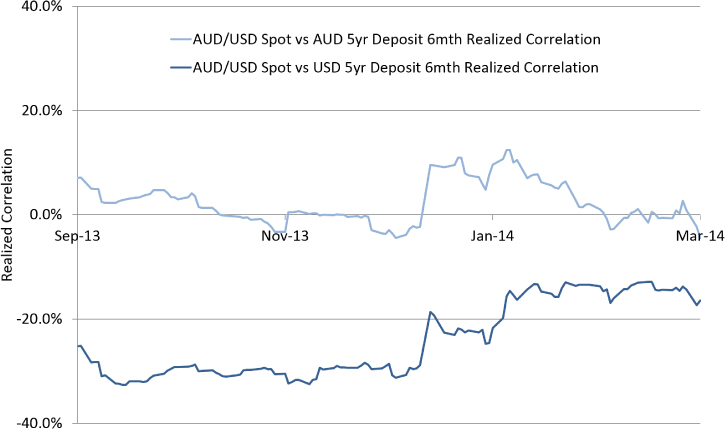
Exhibit 17.20 AUD/USD spot versus interest rate correlation
In this case, the negative correlation between USD (CCY2) interest rates and AUD/USD spot causes forward volatility to be lower than spot volatility.
Increasing interest rates in a particular currency often results in that currency becoming relatively stronger in the spot market because (unless there are major problems with the country) a currency with higher yield is more desirable to own. Therefore, there is often a positive realized correlation between CCY1 interest rates and spot and a negative realized correlation between CCY2 interest rates and spot (as seen in the AUD/USD example above). However, such changes impact the forward in the opposite direction and lead to forward volatility below spot volatility: spot higher as CCY1 interest rates higher → swap points more negative → forward moves less than spot.
The realized volatility of the interest rates themselves can also be calculated and this is shown in Exhibit 17.21. Interest rate volatility reduces over the same period as the realized forward outright volatility versus realized spot volatility difference narrows, as shown in Exhibit 17.14.

Exhibit 17.21 AUD and USD realized interest rate volatility
It is also possible to calculate EWMA correlation. The calculation is analogous to EWMA volatility:
where:
Trading Implied Volatility
There are two main ways to trade implied volatility:
Buy or sell an ATM contract and lock in the implied volatility versus realized volatility difference by delta hedging the gamma exposure on the contract. This is most appropriate at shorter tenors where the main exposure on ATM contracts is gamma rather than vega. For this analysis, absolute levels of implied volatility are compared with absolute levels of realized spot volatility in a similar tenor, ideally adjusted for the impact of economic data releases and holidays. For example, if a 1mth ATM contract can be bought for 8.0% implied volatility and spot consistently realizes 10.0% through to the option maturity, delta hedging the contract will be expected to generate a profit overall.
The frequency of delta hedging is also an important consideration. Within this analysis, the realized volatility versus implied volatility difference is most important and therefore delta should be hedged as often as possible. However, over-trading the delta in a currency pair with a wide bid–offer spread on the underlying can produce negative expected P&L.
Clients sometimes like to trade implied volatility versus realized spot volatility differences with a volatility swap—a forward contract on realized volatility over an agreed period usually using daily spot samples. This is attractive because no delta hedging is required and the exposures remain roughly ATM as spot moves, although bid–offer spreads on volatility swaps are wider than the spread on equivalent ATM contracts. See Chapter 31 for more details.
Buy or sell an ATM contract and then later unwind the trade at better implied volatility levels. This is most appropriate at longer tenors where the main exposure on ATM contracts is vega rather than gamma. For example, if a 1yr ATM contract can be bought at 8.0% implied volatility and then sold back at 9.0% implied volatility that will (almost certainly) generate a profit. For this analysis it is most appropriate to investigate trends in implied volatility and realized volatility since the two measures often trend in the same direction. Consider the spread between implied volatility and realized volatility and look for lags in the data: Are realized volatility changes driving implied volatility changes or vice versa?
When trading ATM contracts, although the initial exposures are primarily gamma and vega, the exposures change as time passes or the market moves. For example, on short-dated vanilla options, as time passes the gamma exposure on short-date contracts increases if spot stays around the strike or reduces if spot moves away from the strike. Therefore, the realized P&L from trading a delta hedged ATM contract is not simply a function of realized volatility versus implied volatility; it is also path dependent.
After trading a long-dated ATM contract, if spot moves, the traded strike is no longer ATM and therefore the implied volatility for the strike becomes a function of the full volatility surface. When this happens the P&L from the trade is no longer simply a function of vega and implied ATM volatility change. Put another way, long-dated ATM options are not contracts for difference on implied volatility.
Clients sometimes like to trade implied volatility using a forward volatility agreement (FVA). This is a pure exposure to forward implied volatility between two dates in the future and therefore requires no delta hedging prior to the first date. See Chapter 31 for more details.
Many of the techniques covered in this chapter work best as relative value tools. Running analysis over multiple currency pairs and tenors can identify outliers that might work as trade ideas although the bid–offer spread on the ATM should always be taken into account. Looking at theoretical midmarket implied volatility levels in obscure crosses often suggests interesting trading opportunities but the spread cross involved in actually executing the trade always needs to be considered.
Finally, many studies conclude that there is a persistent trend that short-dated implied volatility is too expensive. In academic circles this is called the volatility risk premium. One of the key reasons for this risk premium is the preference of traders for the P&L profile from long gamma (many small losses versus few large gains) over the P&L profile from short gamma (many small gains versus few large losses) from a job preservation perspective, particularly on expiry dates when important economic data is released.
Trading Implied Correlation
To trade implied correlation using ATM instruments, a volatility triangle can be constructed as per Exhibit 17.22.
Exhibit 17.22 ATM volatility triangle for trading correlation
Recall from Chapter 16 that to go long implied correlation between CCY1/CCY2 and CCY1/CCY3: Buy the majors and sell the cross, that is,
- Buy CCY1/CCY3 and CCY1/CCY2 ATM contracts.
- Sell a CCY2/CCY3 ATM contract.
To go short implied correlation between CCY1/CCY2 and CCY1/CCY3: Sell the majors and buy the cross, that is,
- Sell CCY1/CCY3 and CCY1/CCY2 ATM contracts.
- Buy a CCY2/CCY3 ATM contract.
The notionals on the ATM contracts should be set such that there is zero initial dephased vega (see Chapter 16) in the major currency pairs to ensure a clean initial implied correlation exposure. As with trading implied volatility, the position can be either delta hedged to generate a P&L based on implied correlation versus realized correlation, or unwound later at a different level of implied correlation. Again though, issues involving exposures changing over time apply, plus transacting all three legs in the volatility triangle may cost a significant amount of spread cross.
Clients sometimes trade implied correlation versus realized correlation differences using a correlation swap—a forward contract on realized correlation using daily samples over an agreed period.
Realized Volatility Convexity
A final point to be aware of when comparing implied volatility with realized volatility is that expected P&L is not linear in realized volatility. Under stylized Black-Scholes assumptions it can be shown that expected P&L from trading a constant long gamma position is proportional to realized volatility squared based on the following equation:

where ![]() is the P&L from gamma trading and
is the P&L from gamma trading and ![]() is theta.
is theta.
If ![]() , the expected P&L from gamma trading will exactly offset the theta paid. But when long gamma, more money is made trading gamma if realized volatility outperforms implied volatility than is lost if realized volatility underperforms implied volatility by the same amount. In other words, there is realized volatility convexity. The practical consequence of this is that implied volatility should be higher than realized volatility for it to be fair value. This effect is another cause of the volatility risk premium (discussed in the Trading Implied Volatility section above).
, the expected P&L from gamma trading will exactly offset the theta paid. But when long gamma, more money is made trading gamma if realized volatility outperforms implied volatility than is lost if realized volatility underperforms implied volatility by the same amount. In other words, there is realized volatility convexity. The practical consequence of this is that implied volatility should be higher than realized volatility for it to be fair value. This effect is another cause of the volatility risk premium (discussed in the Trading Implied Volatility section above).
Exhibit 17.23 shows simulation results demonstrating how P&L from gamma trading changes with realized volatility and hedging interval:
 is proportional to realized volatility squared as per the above formula (i.e., the chart is quadratic, not linear).
is proportional to realized volatility squared as per the above formula (i.e., the chart is quadratic, not linear).- As hedging interval increases, P&L volatility increases. When a very tight hedging interval is applied the P&L volatility is small (this is the essence of the standard Black-Scholes formula derivation).

Exhibit 17.23 Simulation P&L from gamma hedging
Market Instrument Analysis
As well as being linked to the FX spot, forward, and interest rate markets, FX derivatives market instruments can be also assessed against their own history.
ATM Curve
Implied volatility often mean reverts, and volatility cones are a common method of visualizing how the current ATM curve looks versus its history. The lowest and highest implied volatility observed in each tenor over a given period is shown, plus the current level is highlighted. An example volatility cone is shown in Exhibit 17.24.

Exhibit 17.24 AUD/USD 1yr implied volatility cone on Dec. 2013
The idea is, if implied volatility mean reverts (i.e., tends to move back toward its long-run average over time) and it is currently toward the high or low end of the cone, it is more likely to move back toward the middle. This is fine, however, it is vital to consider why the current ATM curve is toward the extreme top or bottom of its historic range. If spot is stuck in a well-established range and realized volatility is still below implied volatility, the ATM curve should be near the bottom of its historical range.
Implied volatility mean reverts because the magnitude of the flows in a given currency pair can be fairly consistent over time and hence similar realized volatility is generated. For traders, the key moments are regime changes, when the level of a financial instrument completely changes from its historical level. For example, during the financial crisis in 2008, implied volatility in most currency pairs jumped significantly higher, as shown in Exhibit 17.25 caused by sharp movements in spots and forwards plus increased uncertainty as shown in Exhibit 17.25.
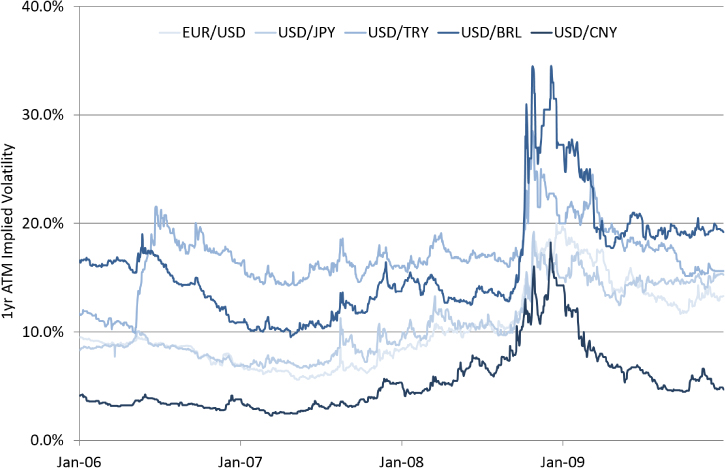
Exhibit 17.25 1yr ATM implied volatility in various currency pairs during the 2008 financial crisis
When trading the ATM curve, it is also important to remember that, in practice, ATM implied volatility usually falls slower than it rises. If spot is range-bound, ATM implied volatility will tend to slowly drift lower over time, but if spot breaks out of its range, ATM implied volatility often jumps higher.
ATM Curve: Slope
If the ATM curve is sharply upward or downward sloping, calendar spread trades may be attractive. For example:
- AUD/USD 3mth ATM implied volatility = 8.2%
- AUD/USD 6mth ATM implied volatility = 11.5%
This implies a 3mth in 3mth forward implied volatility (see the calculation in Chapter 11) of 14.05%—much larger than the current 3mth ATM implied volatility. Therefore, buying 3mth ATM against selling 6mth ATM may be a good trading opportunity. The spread could be transacted with either initially vega-neutral notionals (to reduce P&L volatility from parallel moves in the ATM curve) or initially gamma-neutral notionals (to reduce the P&L volatility caused by spot moves). The trade will make a profit if the ATM curve “flattens” (i.e., the 3mth versus 6mth spread decreases).
The slope of the ATM curve can be assessed over time to identify levels significantly different from history. It is also interesting to compare ATM curve shapes in similar currency pairs. If there is an outlier, perhaps this implies a trading opportunity.
At longer tenors, ATM implied volatility becomes relatively more impacted by interest rate volatility and relatively less impacted by spot volatility:
- If longer-dated realized forward volatility is higher than shorter-dated realized forward volatility, the ATM curve will more likely be upward sloping at longer tenors.
- If longer-dated realized forward volatility is lower than shorter-dated realized forward volatility, the ATM curve will more likely be downward sloping at longer tenors.
Comparing realized spot volatility versus realized forward differences with the shape of the long-dated ATM curve may imply trading opportunities. As usual, though, care must be taken with market conventions.
ATM Curve: Seasonality
In currency pairs where there are significant amounts of corporate FX hedging, ATM volatility around the 1yr tenor can exhibit seasonality as corporates tend to hedge at either the start of the calendar year or at the start or end of their accounting year.
The majority of corporate hedge structures net sell vega and this flow into the market can cause implied volatility to consistently move lower at certain times of the year.
Volatility Smile: Skew
Using time series data, the current skew in the volatility smile can be compared with history using either market risk reversals or skew parameters from a volatility surface model. If the skew of the volatility smile mean reverts, then a quote toward the upper or lower historical limits will more likely move back toward the average. An example of this is shown in Exhibit 17.26.

Exhibit 17.26 Historic USD/JPY 1yr 25d risk reversals
Within this analysis it must be remembered that some currency pairs have persistent positive or negative skew due to client flow, particularly at longer tenors. Plus the risk reversal is often proportional to the ATM so the risk reversal/ATM ratio is often a cleaner measure of skew to use. It can also be interesting to compare ATM changes with risk reversal changes because the two instruments often move together.
Analyzing Value: Skew
In currency pairs where spot and volatility surface moves cause a long risk reversal position to make a profit, traders say the skew is “performing.” Traders seek to buy skew in currency pairs where it is performing and sell skew in currency pairs where it is not.
One possible skew analysis technique compares market risk reversal quotes with the realized spot versus volatility relationship. This ties in with the fact that the main exposure in the risk reversal contract is vanna ![]() as seen in Chapter 12.
as seen in Chapter 12.
A first idea might be to look at the correlation between spot log returns and ATM implied volatility log returns. However, using correlation is not appropriate because it is important to quantify how much spot and ATM implied volatility are moving together, not just how they are moving together. Therefore, the spot versus implied volatility relationship can be modeled using the covariance of spot log returns with implied volatility log returns.
As an aside, correlation ![]() is dimensionless; it expresses how two variables (X and Y) move together:
is dimensionless; it expresses how two variables (X and Y) move together: ![]() or
or ![]() implies perfect linear dependence while covariance
implies perfect linear dependence while covariance ![]() additionally reflects how much the variables are moving. For example, if implied volatility moves up 0.01% for every pip that spot moves up and implied volatility moves down 0.01% for every pip that spot moves down, the correlation between absolute spot changes and absolute volatility changes will be +100%. Now, if implied volatility moves up 0.02% for every pip that spot moves up and implied volatility moves down 0.02% for every pip that spot moves down, the correlation between absolute spot changes and absolute volatility changes will still be +100%. However, the covariance in the second instance will be larger than that of the first.
additionally reflects how much the variables are moving. For example, if implied volatility moves up 0.01% for every pip that spot moves up and implied volatility moves down 0.01% for every pip that spot moves down, the correlation between absolute spot changes and absolute volatility changes will be +100%. Now, if implied volatility moves up 0.02% for every pip that spot moves up and implied volatility moves down 0.02% for every pip that spot moves down, the correlation between absolute spot changes and absolute volatility changes will still be +100%. However, the covariance in the second instance will be larger than that of the first.
Assuming the 25 delta or 10 delta market risk reversal is proportional to the realized covariance of log spot changes versus log implied volatility changes, these time series can be plotted and compared in order to perceive value. This is demonstrated in Exhibit 17.27.

Exhibit 17.27 Time series of EUR/USD 2M risk reversal versus 30-day log spot/log implied volatility changes covariance
This analysis works best at mid tenors (1mth to 6mth) but there are plenty of issues to consider. Most obviously the risk reversal contract is forward looking while the realized covariance is calculated from historical data. Plus strong incorrect trading signals will be generated if there are regime shifts, if there is intervention in the spot market, or if spot is pegged or managed. As with all this historic analysis, trading signals must be considered rather than being blindly followed. It is interesting to run both 10 delta and 25 delta risk reversals through the same analysis to see how they compare in order to identify relatively cheap or expensive 10 delta or 25 delta risk reversals in different currency pairs.
Volatility Smile: Wings
Using time series data, the current wings of the volatility smile can be compared with history. The market butterfly instrument can be used but due to the broker butterfly conventions in high-skew currency pairs the wings versus market butterfly relationship can break down as shown in Chapter 12. Exhibit 17.28 shows AUD/JPY market instruments on January 1, 2008, and January 1, 2009, while Exhibit 17.29 shows the outright 10d and 25d and ATM strikes on the AUD/JPY volatility smiles for the same two dates.

Exhibit 17.28 Historic AUD/JPY market instruments

Exhibit 17.29 Historic AUD/JPY key strikes on the volatility smile
Between January 1, 2008, and January 1, 2009, the 1yr 25d broker butterfly went lower from +0.25% to +0.2% although the wings of the volatility smile are far higher on the later date.
Therefore, rather than using the market butterfly instrument within analysis, a convention-free volatility-of-volatility parameter from a volatility surface model could be used to quantify the wings of the volatility smile. Alternatively, the 10d strike fly (e.g., the average of the 10 delta call and 10 delta put implied volatility less the ATM implied volatility) could be used.
Again, if the wings of the volatility smile mean revert, then a quote toward the upper or lower historical limits will more likely move back toward the average.
Analyzing Value: Wings
In currency pairs where volatility surface moves cause a long butterfly position to make a profit, traders say the wings are “performing.” Traders seek to buy wings in currency pairs where they are performing and sell wings in currency pairs where they are not.
One possible wing analysis technique uses the exposures of a long butterfly contract to compare the P&L generated from the volga  based on historic ATM implied volatility moves with the theta paid to hold the butterfly contract over time.
based on historic ATM implied volatility moves with the theta paid to hold the butterfly contract over time.
The theta from a broker fly contract comes mainly from volga but there are also contributions from gamma and vanna. The gamma exposure can be hedged with a shorter-dated (1wk?) ATM contract and the vanna exposure can be hedged with a risk reversal contract.
By hedging away the other elements, the theta from volga only can be determined. The amount that implied volatility must move per day in order to make back the theta can therefore be calculated. Within this analysis, recall that volga is the second derivative of price with respect to implied volatility and therefore broker fly P&L is not linear in implied volatility, as shown in Exhibit 17.30.

Exhibit 17.30 P&L from a long volga position
The breakeven daily implied volatility change can then be compared with historic daily implied volatility changes but this is rough-and-ready analysis with plenty of issues to be aware of. Most obviously the butterfly contract is forward looking while the realized daily implied volatility moves are calculated from historical data. Plus volga from the butterfly is assumed to stay constant over its life, and using daily data underestimates the realized volatility of implied volatility. In addition, relatively large ATM bid-offer spreads means that, in practice, implied volatility must move further than the midmarket level in order for the value to be captured in practice. Again, this analysis is most effective when applied over different currency pairs, tenors, and deltas to identify relative value trading opportunities.
Discussion on Historical Analysis
Comparing a current market quote with its history is a common analysis technique. One standardized way of quantifying this uses a Z-score, which is a measure of how many standard deviations from the average the most recent sample is:
where ![]() is the most recent sample,
is the most recent sample, ![]() is the sample mean, and
is the sample mean, and ![]() is the sample volatility.
is the sample volatility.
For any mean reverting variable, a negative Z-score is a buy signal and a positive Z-score is a sell signal. If the variable is normally distributed, Z-scores beyond approximately –2.5 and +2.5 are significant.
Again, this analysis fails during regime changes when the level of a financial instrument completely changes from its historical level. Regime changes will often generate strong false trading signals with any systematic analysis. As always, results should be considered carefully before being acted on.
Looking only at recent history is another common issue. Even if value is to be gauged using only quite recent history, it is instructive to check a longer time horizon to determine the historic bounds of the sample. Fundamentally, using historical data as a reference for what the future will look like is sensible and convenient but keep in mind that the future may look very different indeed.
Volatility Smile: Sticky Strike Analysis
Within sticky strike analysis the implied volatility for a specific expiry date and strike is tracked over time. For example, if it is currently January 2015, the implied volatility for a September-23 2015 1.3050 strike can be calculated today, one week ago, two weeks ago, three weeks ago, and so on, using full sets of historic market data. If the implied volatility was stable and then deviates, this may represent a trading opportunity. This analysis is essentially a more sophisticated version of the ATM implied volatility cone and again it relies on implied volatility mean reverting but on a per-expiry and -strike basis rather than in the ATM contract itself at a given tenor. This analysis is appropriate at longer tenors where the main exposure on the trade is vega and the analysis tends to work better in high-skew currency pairs.
Another way to analyze sticky-strikeness is with a scatter chart of historic ATM implied volatility versus spot. Spot higher or lower and ATM volatility higher or lower should tie in with the direction (positive or negative) of the risk reversal in the market. For example, USD/JPY usually has a negative risk reversal, implying higher implied volatility with lower spot. This spot versus ATM implied volatility relationship was very strong during 2007 and 2008 as shown in the scatter plot in Exhibit 17.31.

Exhibit 17.31 USD/JPY 1yr ATM implied volatility versus spot scatter plot showing daily samples from 2007 and 2008
Market Positioning
Understanding how to interpret market positioning is a key skill that traders acquire. In simple terms, determining market positioning involves observing how market participants react to market changes.
Market participants' vega positions impact the FX implied volatility market. Since interbank flow is mostly zero-sum risk transfer it is client trades that generate the net market position. For example, if spot moves sharply and implied volatility stays around the same levels when it would normally be expected to rise, it can be concluded that the market is long vega around current spot because there are fewer market participants buying vega since they are already long. Remember that market vega positioning will change as spot moves.
Market participants' gamma positions impact the FX spot and markets via market participants' delta hedging. If market participants are long gamma in a certain spot region, increased taking profit when delta hedging may cause spot to remain range-bound. If the market is short gamma in a certain spot region, increased stop-loss orders may cause spot to be more volatile. When key spot levels (i.e., round numbered spot values) trade for the first time in recent history, American barriers are often knocked, which can dramatically change the market gamma positioning (see Chapters 23 and 24).
The maximum gamma from vanilla options comes from strikes close to maturity and the spot market often gravitates toward existing strikes with large notionals, called “market strikes.” It is therefore useful to know the big strikes expiring in the market over the next week or so. This information can be sourced from the interbank broker market plus increasing data on expiries is becoming available as a consequence of new market regulations.
Carry Trades
The essence of a successful carry trade is to make money if “nothing happens” (i.e., the market does not significantly move). The classic FX carry trade is driven by the interest rate differentials in a given currency pair—buying the higher yielding currency and selling the lower yielding currency. This can be executed simply by trading the forward. For example, AUD/USD currently has one of the largest interest rate differentials in the universe of G10 currency pairs (although it is a small differential by historical standards). If AUD/USD spot is 0.9400, the 1yr AUD interest rate is 3%, and the 1yr USD interest rate is 0.5%, then AUD/USD 1yr forward will be approximately 0.9170. By buying the 1yr forward at 0.9170 and holding it to maturity, if AUD/USD spot at maturity is above 0.9170, money will be made from the strategy.
Another carry trade variation is achieved within a trading position by holding long cash balances in higher yielding currencies versus holding short cash balances in lower yielding currencies. As described, cash balances generate income based on their yield and the net money earned from the long and short cash balances can also be thought of as carry. Interest rate differential carry trades are particularly popular in currency pairs that contain one high-yielding emerging markets currency and one low-yielding G10 currency.
In quiet markets carry trade positions build over time; but if there is a market shock, the positions can rapidly unwind as everyone exits the same trade at the same time. The longer the carry trade builds up, the more dramatic the unwinding when it occurs. Exhibit 17.32 shows AUD/USD spot from 2006 to 2009. Part of this spot rise was due to increasing carry trade positioning. Each time investors went long AUD versus short USD within carry trades, at maturity they had gained not only from the interest rate differential but also the currency appreciation.

Exhibit 17.32 AUD/USD spot from 2006 to 2009
This strategy worked really well until it went spectacularly wrong. The P&L distribution from carry trades is that of many small gains versus few large losses although academic studies often conclude that there is a long-term bias that gives carry trades a positive expected P&L. In practice, though, losses incurred in 2008 would cause any systematic trading strategies based on a pure carry trade methodology (buy the high-yielding currencies versus sell the low-yielding currencies) to be permanently shut down.
The link between interest rate differentials and the risk reversal is partly driven by carry trade positioning, which can unwind rapidly and cause a big increase in implied volatility to the high side of the risk reversal. Therefore FX carry trades are particularly popular in currency pairs with relatively high interest rate differentials but low implied volatility.
A multitude of variations on the carry trade theme are possible. In vanilla FX derivatives there can be carry strategies based on the ATM curve, the volatility smile, the interest rate differential, or combinations of all three. The common factor is that all carry strategies decay positively, providing the market stays static.
One simple FX derivatives carry trade involves trading a vanilla ATM spot versus ATM forward spread. This can be either a put spread or a call spread, depending on whether the forward is above or below spot. The two cases are shown in Exhibits 17.33 and 17.34.

Exhibit 17.33 Call spread carry trade

Exhibit 17.34 Put spread carry trade
Again, the idea is that the spread will pay out if spot remains at its current level. This strategy can be analyzed as a ratio of the cost of the spread over the potential maximum payoff. Ratios over 2.5 are often thought of as interesting. This carry trade is a function of the forward drift and the volatility smile.
