Chapter 12
Volatility Smile Market Instruments and Exposures
In the interbank broker market, at each market tenor, three market instruments define the volatility smile:
- At-the-money (ATM) contracts define the implied volatility for a specific strike close to (or exactly at, depending on the market conventions for a given currency pair) the forward for the given tenor.
- Butterfly (Fly) contracts define the implied volatility differential between the wings of the volatility smile and the ATM—a measure of the height of the wings of the volatility smile.
- Risk reversal (RR) contracts define the implied volatility differential between strikes above and below the ATM—a measure of how skewed or tilted the volatility smile is.
Butterfly and risk reversal contracts are most often quoted at 25 delta (25d) and 10 delta (10d) strikes. An example run of market instruments at market tenors is shown in Exhibit 12.1.
Exhibit 12.1 Example EUR/USD market instruments at market tenors
Exhibit 12.2 shows the relative positioning of different deltas within a stylized volatility smile. Recall that it is the market convention to trade the out-of-the-money side.
Exhibit 12.2 Deltas quoted within the volatility smile
The following approximations link the ATM, 25d butterfly, and 25d risk reversal instruments with the implied volatilities for the outright 25d call and put options at a given tenor:
Therefore:
Exhibit 12.3 shows how these market instruments fit into the volatility smile.
Exhibit 12.3 25 delta market instruments within the volatility smile
These approximations were generalized into a single formula for any delta by Allan M. Malz in 1997:
In words, the ATM represents the central reference point, the butterfly lifts the wings symmetrically higher on both sides, and the risk reversal tilts the smile one way or the other. As mentioned in Chapter 7, put deltas are often quoted without the negative sign. Positive put delta values between 0% and 100% are used in the Malz formula.
If butterfly and risk reversal contracts at all deltas are zero, the volatility smile is flat as shown in Exhibit 12.4, and any strike at that tenor will be assigned the same midmarket implied volatility.
Exhibit 12.4 Volatility smile with zero risk reversal and zero butterfly
If the butterfly increases, the wings of the volatility smile rise symmetrically as shown in Exhibit 12.5.
Exhibit 12.5 Volatility smile with zero risk reversal and positive butterfly
With a positive risk reversal, strikes above the ATM have a higher implied volatility than the equivalent delta strikes below the ATM. This is shown in Exhibit 12.6.
Exhibit 12.6 Volatility smile with positive risk reversal
With a negative risk reversal, strikes below the ATM have a higher implied volatility than the equivalent delta strikes above the ATM. This is shown in Exhibit 12.7.
Exhibit 12.7 Volatility smile with negative risk reversal
Market Instrument Vega Exposures
The reason for describing the volatility smile with ATM, butterfly, and risk reversal instruments becomes clearer when the implied volatility exposures of the three market instruments are examined. The key implied volatility exposures are:
: sensitivity of price to changes in implied volatility.
: sensitivity of vega to changes in spot. Vanna can also be thought of as the sensitivity of delta to changes in implied volatility, i.e., 
since 
.
: sensitivity of vega to changes in implied volatility. Volga is the second derivative of price with respect to changes in implied volatility. Therefore, volga is to implied volatility as gamma is to spot and as the volatility of implied volatility rises, the expected P&L from a long volga trading position increases.
ATM Exposures
The vega profile for a long ATM vanilla option has a single peak around current spot. Exhibit 12.8 shows how, at higher volatility, the vega profile is wider since the spot distribution is wider, but vega is unchanged at the initial spot.
Exhibit 12.8 Vega profile from long ATM at different implied volatility levels
Therefore, a long ATM contract at inception has the following exposures:
- Vega: positive exposure
- Vanna (the gradient of the vega/spot chart): no exposure
- Volga (the difference between the vega profiles for different implied volatility levels at the initial spot level): no exposure
Vanna with spot above the strike is negative since vega rises into the (now) downside peak. Vanna with spot below the strike is positive since vega rises into the (now) topside peak. The vanna profile from a long ATM option is shown in Exhibit 12.9.
Exhibit 12.9 Vanna profile from long ATM
Recalling the dual interpretation of vanna as 
or 
, consider an out-of-the-money topside call option (i.e., strike above spot). At current implied volatility the strike has 25% delta. If implied volatility rises, the chance of the strike ending in-the-money at maturity increases as the distribution widens and hence delta rises. Therefore, this option has a long vanna exposure.
Likewise, consider a downside (in-the-money) call strike (i.e., strike below spot). At current implied volatility the strike has 75% delta. If implied volatility rises, the chance of the strike ending in-the-money at maturity decreases as the distribution widens and hence delta falls. Therefore, this option has a short vanna exposure.
Volga with spot above or below the ATM strike is positive since long wing vanilla options generate positive volga. The volga profile from a long ATM option is shown in Exhibit 12.10.
Exhibit 12.10 Volga profile from long ATM
Risk Reversal Exposures
For a risk reversal contract, again, higher implied volatility moves the vega profile wider but at initial spot the vega exposure is unchanged at zero. This is shown in Exhibit 12.11. It is important to understand that these exposure profiles are generated with fixed strikes, equivalent to calculating the exposures immediately after trading the contract.
Exhibit 12.11 Vega profile from risk reversal (buying topside) at different implied volatility levels
In this instance, buying the risk reversal means buying the topside strike versus selling the downside strike but in different currency pairs or tenors this may be the other way around. Therefore, a long risk reversal position can give either a long or short vanna exposure, depending on whether topside strikes are at higher or lower implied volatility than the equivalent delta downside strikes. If the topside strikes have a higher implied volatility, traders say the risk reversal is “for topside,” whereas if downside strikes have a higher implied, traders say the risk reversal is, yes, “for downside.” In a currency pair where the risk reversal is for downside, a long risk reversal position initially gives a short vanna position as shown in Exhibit 12.12.
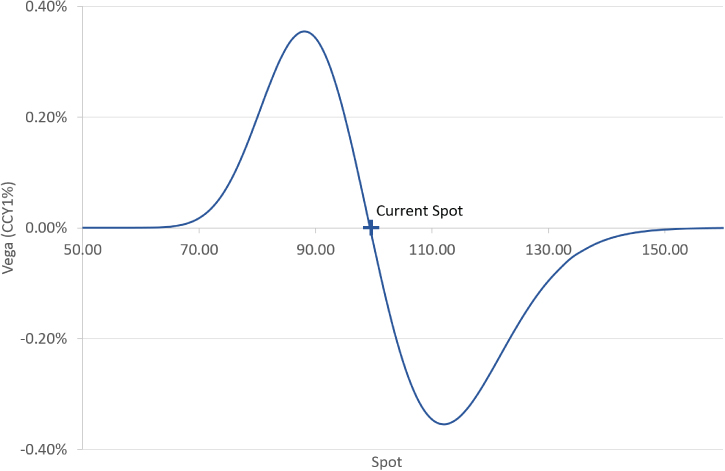
Exhibit 12.12 Vega versus spot profile from risk reversal (buying downside)
Notice that these vega profiles aren't perfectly rotationally symmetric since vega persists further to the topside. This occurs because the Black-Scholes formula is stated in log-return terms, which causes distances in spot space to compress toward zero. A stylized vega versus spot log-return graph for a risk reversal is rotationally symmetric as shown in Exhibit 12.13.
Exhibit 12.13 Vega versus log spot profile from risk reversal (buying downside)
The vanna exposure on a risk reversal does not persist over all spot levels. Rather it is maximized at the initial spot as shown in Exhibit 12.14.
Exhibit 12.14 Vanna profile from risk reversal (buying topside)
Therefore, a long risk reversal contract at inception has the following exposures:
- Vega: no exposure
- Vanna: positive or negative exposure depending on whether the risk reversal is “for topside” or “for downside” (i.e., whether topside or downside strikes are priced at higher implied volatility within the volatility smile)
- Volga: no exposure
Butterfly Exposures
A long butterfly contract is constructed using a long strangle (long wings) and a short straddle (ATM) with the ATM notional set such that the structure is initially vega-neutral and the call and put legs in the strangle have the same notional and delta. Exhibit 12.15 shows the vega profile from a long butterfly. Again, the butterfly strikes are fixed and hence the chart shows how the vega exposure changes at different implied volatility levels after trading.
Exhibit 12.15 Vega profile from long butterfly at different implied volatility levels
The volga exposure on a butterfly does not persist over all spot levels. Rather it is maximized at the initial spot as shown in Exhibit 12.16.
Exhibit 12.16 Volga profile from long butterfly
A long butterfly contract at inception has the following exposures:
- Vega: no exposure (by construction)
- Vanna: no exposure
- Volga: positive exposure
Summary
Within this stylized analysis using a flat volatility smile and ignoring issues like adaption (explained in Chapter 14) and broker fly strike placement (explained later in this chapter), the three different market instruments give the three unique vega exposures at inception shown in Exhibit 12.17.
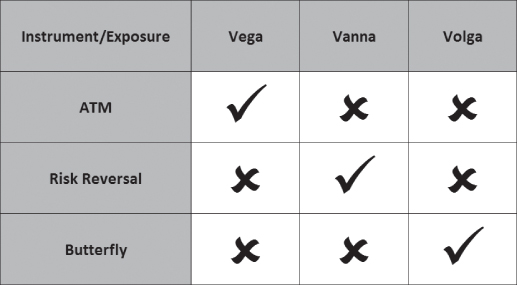
Exhibit 12.17 Vega exposures from market instruments
In practice this means that:
- ATM contracts are used to trade the level of implied volatility because their main exposure at inception is vega
. - Risk reversal contracts are used to trade the spot versus implied volatility relationship because their main exposure at inception is vanna
. - Butterfly contracts are used to trade the volatility of implied volatility because their main exposure at inception is volga
.
Finally, it is mildly interesting to observe that the vanna profile of the ATM takes the same shape as the vega profile of the risk reversal while the volga of the ATM takes the same shape as the vega of the butterfly.
Risk Reversal Contract
The Black-Scholes formula assumes that the volatility of the underlying is constant. In practice, implied volatility changes depending (amongst other things) on how spot moves. Plus, in the market there is often differing supply and demand for topside or downside optionality, which leads to an asymmetric volatility smile.
The FX derivatives market expresses the amount of skew in the volatility smile via the risk reversal contract. Specifically, the risk reversal gives the differential between the call strike implied volatility and the put strike implied volatility for the same tenor and delta.
In the interbank broker market, risk reversals are quoted in positive terms, with the direction also quoted. For example, in USD/ZAR, if the 1yr 25d call is priced at 15.5% implied volatility and the 1yr 25d put is priced at 11.25% implied volatility, the 1yr 25d risk reversal would be quoted as “4.25% USD calls over,” meaning that the USD call volatility is higher than the USD put volatility. In some currency pairs, it is market convention to quote the risk reversal direction in CCY2 terms. USD/JPY risk reversals are quoted as, for example, “1.4% JPY calls over” if the implied volatility for the downside strike is 1.4% higher than the implied volatility for the topside strike. As noted, buying the risk reversal always means buying the call or put strike with the higher volatility, and selling the other leg.
The delta used to calculate the risk reversal strikes is sometimes spot delta and sometimes forward delta, depending on market convention. Most often, short-dated G10 risk reversals are quoted using spot delta strikes while long-dated G10 and emerging market risk reversals are quoted using forward delta strikes. Whichever delta convention is used to generate the strikes will also be used to delta hedge the transaction if dealt.
When trading a risk reversal, particularly if it is long-dated, it is important to pay attention to exactly which strikes are being transacted. Strikes traded within a risk reversal are the outright strikes—the same strikes as if same-tenor and same-delta call or put vanillas are traded in isolation.
If a currency pair had a completely flat volatility smile, the risk reversal strikes would be positioned approximately symmetrically around the ATM strike in log-space. Therefore, the topside strike will be further away from the ATM than the downside strike in regular spot space. At short maturities this effect is small but at longer maturities the impact can be significant.
Additionally, if a currency pair has a large forward drift, at longer maturities the ATM strike will be far from current spot and it is possible that, for example, if the forward drift is large positive, the 35d put strike is positioned close to current spot.
Remembering that out-of-the-money strikes are always traded within a risk reversal contract, the volatility smile also impacts risk reversal strike placement:
- If the implied volatility for a given delta is higher on the smile, the strike moves further away from the ATM; think about the increasing chance of ending up in-the-money at higher volatility.
- If the implied volatility for a given delta is lower on the smile, the strike moves closer to the ATM; think about the decreasing chance of ending up in-the-money at lower volatility.
Finally, market conventions play an important role in risk reversal strike placement. If the premium currency is CCY1 and the ATM is a zero-delta straddle, the ATM strike is lower than the forward (see Chapter 8) and the risk reversal strikes are relatively lower also.
Exhibit 12.18 shows a typical volatility smile in AUD/JPY—a CCY1 premium pair with a large downside risk reversal.
Exhibit 12.18 AUD/JPY volatility smile
- The AUD call strike is located on a relatively flat part of the smile, so the implied volatility from the relatively lower strike (caused by a CCY1 premium) is not too different.
- The AUD put strike is located on a steeply sloping part of the smile, so the implied volatility from the relatively lower strike (caused by a CCY1 premium) is significantly higher.
This effect causes AUD/JPY risk reversal contracts to be valued at higher implied volatility levels and the impact gets larger for long-dated options. In practice this means that care must be taken when assessing the term-structure of long-dated risk reversals or comparing risk reversals between currency pairs with different market conventions.
What Drives the Risk Reversal in the Market?
The risk reversal contract expresses the prevailing market preference for topside versus downside optionality. This preference is a function of market positioning (see Chapter 17) but it also depends on the market's perception of expected spot moves, realized spot volatility, and implied volatility changes.
At shorter tenors the risk reversal is largely driven by expectations of spot moves and realized spot volatility. For example, if shorter tenor risk reversals go more for downside, that may imply the market expects that if spot goes lower, spot will be more volatile. Or it may imply that the market expects that there is an increased chance that spot will move lower.
At longer tenors the risk reversal is largely driven by expectations of spot moves and implied volatility changes. For example, if longer tenor risk reversals go more for downside, that may imply that the market expects that if spot goes lower, implied volatility will rise more. Or it may imply that the market expects that there is an increased chance that spot will move lower.
The risk reversal contract can be thought of as a measure of the relative strength of the two currencies in the currency pair. In a USD versus emerging market currency pair (e.g., USD/TRY or USD/BRL), the risk reversal will invariably be positive because there is a far higher chance of a sharp devaluation of the emerging market currency (i.e., spot jumps higher) than the USD. When spot jumps, implied volatility invariably rises and therefore a long risk reversal position with a long vega exposure to the topside will make money.
This idea of the relative strength of currencies also links to the interest rate differential (i.e., carry; see Chapter 17). Usually, the larger the interest rate differential in a given currency pair, the larger the risk reversal. This relationship becomes more important at longer tenors. Buying the higher-yielding currency and selling the low-yielding currency to benefit from the carry and then buying the risk reversal for protection from a blowup is a classic trading strategy in emerging market currency pairs.
Historically, interest rate differentials and risk reversals were highly correlated since low interest rate currencies (e.g., JPY or CHF) implied a more stable country with lower growth potential while high interest rate currencies (e.g., BRL or TRY) implied a country with higher growth potential but more political, social, or economic instability. However, since the 2008 financial crisis most G10 currency pairs have low interest rates and the link between carry and risk reversals has weakened, although it remains an important factor. Exhibit 12.19 shows the relationship between 1yr interest rates and 1yr 25 delta risk reversals in 70 of the most liquid currency pairs as of October 1, 2014.
Exhibit 12.19 1yr interest rate differential versus 1yr 25d risk reversal scatter plot
Trading the Risk Reversal
In the same way that realized volatility is often lower than implied volatility (see Chapter 17 for details), realized skew is often less than implied skew (i.e., it costs more to buy and hold the risk reversal position than can be made back from trading the spot versus implied volatility relationship). This implies that there is a risk premium associated with holding a long risk reversal position, which makes sense since the risk reversal offers protection from the most likely extreme market moves. When spot breaks out of recent trading ranges there is often a risk reversal overvaluation as the risk premium increases, particularly at longer tenors.
For risk reversals, as for all other financial instruments, traders must be careful not to fall into the trap of believing that the status quo will prevail indefinitely. Exhibit 12.20 shows a chart of USD/JPY 1yr 25 delta risk reversals over ten years with trader comments at various points.
Exhibit 12.20 USD/JPY 1yr 25d risk reversals from May 2002 to November 2012
In the interbank broker market, the risk reversal is traded in terms of the volatility differential between the two strikes. After a transaction is agreed, the actual implied volatilities must be agreed. For example, two banks could agree to transact an AUD/USD 1yr 25d RR at 2.6% AUD puts over, but then the risk reversal buying bank wants 11.6% on the AUD put (and therefore 9.0% on the AUD call) while the RR selling bank wants 11.4% on the AUD put. This disagreement occurs for two reasons:
- Strike placement. The call and put strikes are backed out of an inverted Black-Scholes formula. For the risk reversal buying bank, the higher the agreed implied volatilities, the further away from the ATM both risk reversal strikes are positioned. The higher volatility side of the volatility smile is steeper than the lower volatility side. Therefore, by pushing the strikes further away from the ATM, the risk reversal buying bank gets a long strike which is marked even higher (i.e., better) on the volatility smile.
- Adapted vega (explained in Chapter 14). Buying a risk reversal results in a short adapted vega exposure. Therefore, the risk reversal buying bank wants the highest implied volatilities possible so they get short adapted vega from the highest possible level. Likewise, the risk reversal selling bank wants the lowest implied volatilities possible so they get long adapted vega from the lowest possible level.
Traders must check the proposed market data and only agree to trade at correct implied volatility levels. There will be occasions where transacting the risk reversal is more important than these second-order effects but traders should always calculate the P&L difference from mid implied volatility levels so they know how much additional “spread” the transaction is costing.
Finally, traders use their short-dated risk reversal exposures to manage their delta positions. For example, in a currency pair with a risk reversal for topside, if a trader is long short-dated risk reversal and spot jumps higher, even if the trader has not seen any implied volatility prices in the market it is clear that implied volatility will be higher. Due to the long vanna 
exposure from the risk reversal the trader knows that their position will be longer delta. Assuming USD is CCY1, if vanna is long USD20m and implied volatility is approximately 1% higher, delta will be USD20m longer and additional delta can be sold at the higher spot. In effect, the long risk reversal position creates delta changes equivalent to being long gamma.
25d versus 10d Risk Reversal Contracts
Exhibit 12.21 shows vega profiles from 25d and 10d risk reversals.
Exhibit 12.21 25d risk reversal vega profile versus 10d risk reversal vega profile
The wider positioning of the strikes within the 10 delta risk reversal causes the vega peaks to be positioned further away from the ATM and the peak vega exposures to be larger since the vega offsets less when the strikes are further apart.
The risk reversal quotes at different deltas are linked. Investigating these relationships is useful for understanding the volatility smile. In many pairs, only 25d risk reversals are regularly quoted in the interbank broker market. The relationships between risk reversals at different deltas are called risk reversal multipliers. In almost all currency pairs, at lower delta the risk reversal quote increases, as shown in Exhibit 12.22.
Exhibit 12.22 25d and 10d risk reversals on the volatility smile
Within the Malz volatility smile formula, substituting 10% put delta and 10% call delta into the formula gives:
Therefore:
This 25d/10d multiplier of 1.6 is a touch lower than values typically observed in the market for liquid currency pairs where the value is usually around 1.8. Risk reversal multipliers are usually fairly stable in liquid currency pairs.
Another method for calculating risk reversal multipliers is to assume that the cost of vanna remains constant. This method is back-of-the-envelope, old-school, and circular, but it gives some intuition as to how risk reversal contracts at different deltas are linked. Exhibit 12.23 shows vega for AUD/USD 1yr outright strikes and vanna for AUD/USD 1yr long risk reversals over a range of deltas (AUD puts over hence short vanna).
Exhibit 12.23 AUD/USD 1yr outright strike vega and 1yr long risk reversal vanna
The 1yr AUD/USD 25d risk reversal is –2.5%. Therefore, this risk reversal contract “costs” approximately 2.5% volatility 
0.31% vega = 0.775 AUD% more to buy in premium terms than if the risk reversal was 0%.
The 1yr AUD/USD 25d RR has –4.2% vanna while the 1yr AUD/USD 10d RR has –4.1% vanna. If the premium cost of vanna is constant, the 10d RR should cost (4.1/4.2 =) 0.975 of the 25d RR in premium terms. If the 10d RR costs (0.775% × 0.975 =) 0.755% in premium terms, that equates to a 10d risk reversal quote of (0.755%/0.17% vega =) –4.45%, which is (–4.45%/–2.5% =) 1.775× the 25d risk reversal.
For 1yr AUD/USD, the above methodology gives risk reversal multipliers shown in Exhibit 12.24. These multipliers are close to values often observed in the market.
Exhibit 12.24 AUD/USD 1yr risk reversal multipliers
Cross Risk Reversals
Given 25d risk reversals in EUR/USD and USD/JPY, how can the 25d risk reversal in EUR/JPY be calculated?
In some cases, cross risk reversals can be calculated as a fixed offset to the risk reversal in one of the major pairs. This methodology is suitable if there is clearly a dominant currency within the pair that will contribute the vast majority of the skew. For example, EUR/HKD risk reversals can be generated off EUR/USD risk reversals since USD/HKD is a managed currency pair with low implied volatility.
A copula approach, in its most simple form, takes probability densities (see Chapter 13 for more information on probability density functions) generated by the major volatility smiles at a given tenor and builds a cross volatility smile assuming a static correlation between the major pair spots. In some cases this works well but in others it fails to produce a smile close to the market. A more effective variation uses the copula to generate changes in the cross risk reversal rather than generating the absolute level.
Another possible approach is to look at a system of risk reversals in many currencies against each other, imply a relative “strength” parameter for each currency, and then use this to generate cross risk reversals (taking the level of the ATM into account each time). Alternatively, the realized historic spot versus volatility relationship can be used to imply a cross risk reversal using a regression-style calculation.
Cross risk reversals are a tricky area and this section barely scratches the surface. Different banks take different approaches but flexibility is important; finding a single method that works for all crosses all the time is very difficult.
Butterfly Contract
The Black-Scholes formula assumes constant volatility. In practice, volatility (both implied and realized) itself is volatile. This causes wing vanilla options to be often priced at higher implied volatility than the ATM due to the volga (second derivative of implied volatility) they contain.
The FX derivatives market expresses the height of the wings of the volatility smile via the butterfly contract, quoted as the average of the same-delta call strike implied volatility and put strike implied volatility less the ATM volatility at a given tenor.
Strike placement is very important within the butterfly contract. The butterfly contract that is quoted and traded in the interbank broker market is called the broker fly. The strikes within the 25d broker fly are not the outright 25d call and 25d put strikes. Therefore, the strikes within the same-tenor and same-delta risk reversal and broker fly are different. The butterfly constructed using the outright 25d call and 25d put strikes is sometimes called a strike fly but this instrument is rarely traded in practice.
The broker fly is a messy concept, but put as simply as possible:
The broker fly is the implied volatility at which the premium of the call and the put generated and priced using the ATM + broker fly volatility is equal to the premium of the same strikes on the full volatility smile.
This statement can be broken down into two parts:
Part 1: The ATM + broker fly volatility is used to generate the call and put strikes within the broker fly. Crucially, this means the risk reversal/skew is not taken into account within broker fly strike placement.
Example: In EUR/USD, spot is 1.2600, the 1yr forward is 1.2660, the 1yr ATM strike is 1.2740, and the 1yr ATM implied volatility is 11.5%:
- Outright 25d call strike = 1.3690 (10.80% volatility)
- Outright 25d put strike = 1.1695 (13.15% volatility)
If the 25d broker fly volatility is +0.40%:
- Broker fly 25d call strike = 1.3810. The 25d broker fly call strike is further away from the ATM strike than the outright 25d call strike since it is generated using 11.9% volatility (11.5% ATM volatility + 0.4% broker fly volatility) rather than 10.8% volatility on the smile.
- Broker fly 25d put strike = 1.1775. The 25d broker fly put strike is closer to the ATM strike than the outright 25d put strike since it is generated using 11.9% volatility rather than 13.15% volatility on the smile.
In general, on the higher side of the volatility smile, the strike within the broker fly will be closer to the ATM than the same delta outright strike since broker fly strike volatility will be lower than the smile strike volatility. While on the lower side of the volatility smile, the strike within the broker fly will be further away from the ATM than the same delta outright strike since broker fly strike volatility will be higher than the smile strike volatility. Exhibit 12.25 gives a diagram showing broker fly strike placement.
Exhibit 12.25 Broker fly strike placement
Particularly at long-dated maturities or in high skew currency pairs the difference between outright strikes and broker fly strikes can be large.
Example: In AUD/JPY, spot is 80.25, the 5yr forward is 63.85, the 5yr ATM strike is 58.20, and the 5yr ATM implied volatility is 19.25%:
- Outright 25d put strike = 46.05 (22.55% volatility)
- Outright 25d call strike = 79.10 (14.15% volatility)
- Broker fly 25d put strike = 49.60 (30% forward delta on the smile)
- Broker fly 25d call strike = 82.80 (20% forward delta on the smile)
Part 2: The combined premium of the call and put options priced using the ATM + broker fly volatility is equal to their combined premium priced using the full volatility smile. Exhibit 12.26 shows this in a pricing tool.
Exhibit 12.26 Pricing tool showing broker fly premiums
The broker fly strikes are generated in leg 1 and inputted in legs 2 and 3. Look at the premiums: The cost of the strangle (the call plus the put) at ATM + broker fly volatility is the same as the cost of the call using the full smile plus the cost of put on the full smile (8.49% = 5.65% + 2.84%).
Some long-dated AUD/JPY volatility surface instruments are shown in Exhibit 12.27. The ATM and RR are both rising at longer tenors but the 25d broker flies are going more negative. This is a counterintuitive result because a higher ATM and larger skew is intuitively linked with higher wings within the volatility smile. In fact, the broker fly goes more negative because the broker fly contract contains vanna exposure when valued on the smile caused by the strike positioning.
Exhibit 12.27 AUD/JPY Volatility Surface Instruments
| Tenor | ATM | 25d RR | 25d Fly |
| 1yr | 15.3% | −5.7% | +0.1% |
| 2yr | 16.6% | −7.2% | −0.5% |
| 3yr | 17.0% | −7.8% | −1.0% |
| 4yr | 18.3% | −8.1% | −1.5% |
| 5yr | 19.25% | −8.4% | −2.0% |
In a CCY1 premium pair a long broker fly contains long vanna exposure because the CCY1 premium pulls all strikes lower. This makes the long topside strike relatively closer and the long downside strike relatively further away, resulting in long vanna.
In a CCY2 premium pair, if the risk reversal is for topside, a long broker fly contains short vanna exposure, whereas if the risk reversal is for downside, a long broker fly contains long vanna exposure.
These vanna exposures significantly impact the volatility price of the broker fly contract in CCY1 premium currency pairs. If the risk reversal is for topside, the broker fly quote will be pulled higher due to the long vanna (long risk reversal exposure). If the risk reversal is for downside, the broker fly quote will be pulled lower due to the long vanna (short risk reversal exposure), as in the above AUD/JPY case.
What Drives the Butterfly in the Market?
The butterfly contract expresses the prevailing market preference for wing optionality compared with ATM optionality. This preference is a function of market positioning (see Chapter 17) but it also depends on the market's perception of expected realized and implied volatility changes.
At shorter tenors the butterfly reflects the prevailing market preference for wing gamma (i.e., gamma away from current spot) while at longer tenors the butterfly is largely driven by market expectations of how volatile implied volatility will be, plus it also reflects the prevailing market preference for wing vega.
In emerging market currency pairs, traders buy the butterfly contract as protection from sharp moves in spot and implied volatility. The cost/benefit of holding a long butterfly position is compared with the cost/benefit of holding a long risk reversal position or holding a long gamma position.
Trading the Butterfly
In the interbank market, butterfly contracts are not traded as frequently as risk reversal contracts. Butterfly contracts in a given currency pair might not trade for a few days at a time. However, traders update the wing parameters within their volatility surface more frequently in order to match implied volatility prices or trading levels on specific contracts.
25d versus 10d Butterfly Contracts
Exhibits 12.28 and 12.29 give the vega and volga profiles for 25d and 10d butterflies.
Exhibit 12.28 25d butterfly vega versus 10d butterfly vega profiles
Exhibit 12.29 25d butterfly volga versus 10d butterfly volga profiles
As shown in Exhibit 12.28, both 10d and 25d butterfly contracts give sharp changes in vega away from current spot. The 10d flies have over double the peak vega in the wings versus the 25d flies for equal wing notional, plus a wider distribution. The 25d butterflies can therefore be traded in large size without significantly impacting the trading position. Within 25d broker butterflies in CCY1 premium pairs the strikes can be positioned so closely together that they can generate large localized vanna exposures. Believe me, I found this out the hard way.
Exhibit 12.29 shows how the long volga at current spot goes flat and then short as spot moves away from the current level in the wings and how 10d flies give a wider (better) volga distribution than 25d flies. Within a butterfly contract, the maximum volga exposure occurs at current spot. Therefore, if the aim of the trader is to get longer volga at higher or lower spot levels, the butterfly (particularly the 25d butterfly) is not necessarily the best contract to trade.
Finally, it is worth noting that the broker fly strike placement prevents the existence of stable 25d/10d butterfly multiples in most currency pairs.
Volatility Smile Risk Management
When trading an FX derivatives position it is important to understand how the vega exposure will be impacted as spot and implied volatility changes, and also the exposures to the smile instruments themselves. The smile position is therefore monitored using two sets of exposures:
- Vanna
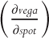and volga 
explain how the vega position changes as spot and implied volatility changes. - Rega
and sega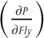 
explain how P&L changes as the risk reversal and butterfly prices change. Both rega and sega are quoted to whichever delta contracts are used to build the volatility surface. For example, if only 25 delta risk reversals are used to build the volatility smile, only 25 delta rega is meaningful. That rega represents the P&L generated from revaluing all contracts in the position using a volatility surface with changed 25 delta risk reversal contracts.
Vanna is usually quoted as change in vega for a change in spot, or, recalling the dual interpretation of vanna, the change in delta for a 1% change in ATM implied volatility. Therefore, if a trading position is long USD1m vanna, if spot moves 1% higher, vega will get longer by USD10k. Or, if ATM implied volatility moves 1% higher (i.e., from 8% to 9%), delta will get longer by USD1m.
Volga is usually quoted as a change in vega for a 1% move in ATM implied volatility. Therefore, if a trading position is short USD250k volga, if implied volatility rises by 0.1%, vega will get shorter by USD25k. As mentioned, volga is a second derivative like gamma. A long volga exposure therefore means that vega can be sold when implied volatility rises and bought when implied volatility falls.
Rega is usually quoted as the sensitivity to a 1% change in the volatility price of the risk reversal instrument. Therefore, if a trading position is long USD150k of 25 delta rega, if the 25d risk reversal moves from +0.8% to +1.0%, a P&L change of +USD30k will be generated.
Sega is usually quoted as the sensitivity to a 1% change in the volatility price of the butterfly instrument. Therefore, if a trading position is long USD100k of 25 delta sega, if the 25d butterfly moves lower by 0.1%, a P&L change of –USD10k will be generated.
Like other exposures, within a trading position; vanna, volga, rega, and sega will not be static; they will change as spot or ATM implied volatility moves, so all have their own higher-order derivatives (e.g., 
or 
, etc.). However, when analyzing derivatives trading positions it is often better to view, for example, vanna exposures within a spot ladder or implied volatility ladder rather than considering higher-order sensitivities at current spot only.
For reference, the rega on a risk reversal is approximately the average of the two absolute strike vegas while the sega on a butterfly is approximately the sum of the two wing strike vega exposures. In addition, a 25d topside strike in isolation will have a 25d rega approximately equal to half of its vega since, for example, a +0.1% change in the risk reversal will roughly move the implied volatility for the 25d call strike up by 0.05% and the implied volatility for the 25d put strike down by 0.05%.
The quotation conventions used for these smile exposures will differ from trading desk to trading desk. Plus, although rega and sega here are specifically the sensitivities to the market risk reversal and butterfly instruments, they can more generally be thought of as the sensitivities to the parameters that control the skew and wings within the volatility surface construction.
Risk reversal contracts have vanna and rega exposures while butterfly contracts mainly have volga and sega exposures. It is therefore natural to assume that trading positions that have vanna exposures also have corresponding rega exposures and trading positions that have long volga exposures also have long sega exposures. However, when trading a portfolio of vanilla options in high-skew pairs or when trading exotic contracts the links between vanna and rega and between volga and sega can break down. For example, a trading position might be flat volga but long sega. Therefore, traders must monitor all these exposures within their risk management.
Volatility Smile Construction Methods
The Malz volatility smile formula shows how it is possible to construct a volatility smile directly from the market instruments but in practice the process is far more complicated. As with the ATM curve, the volatility smile can be either an input or an output.
Some trading desks express the volatility smile using the market instruments directly in a process that must adjust for market conventions and strike placement issues. Within this approach, since only 25 and 10 delta market instruments are liquid, if market instruments are used to build the volatility surface, volatilities are defined only between 10 delta puts on the downside and 10 delta calls on the topside. Implied volatilities beyond the 10 delta strikes must either be controlled using extrapolation or generated automatically using a model like Stochastic Volatility Inspired (SVI)-see Gatheral's book in Further Reading for more information.
Other trading desks use models such as Hagan, Kumar, Lesniewski, and Woodward's SABR model, with traders updating the parameters of the model such that the market instruments output by the model at market tenors match the market.
In addition, the volatility smile must be interpolated between tenors. Trading desks develop their own methods for this, interpolating in e.g., delta terms, strike terms, or model parameter terms.
Other asset classes express volatility surfaces in different ways. In interest rate derivatives, the SABR model has become the market standard while in equity derivatives, implied volatility is quoted at different percentage distances from the current stock price. It is important to understand that there is nothing about the FX derivatives market that makes the ATM, risk reversal, and butterfly approach the only possible way of representing the volatility smile. It is a market convention that has developed and become the standard over time, but other parameterizations would be equally valid.