Chapter 6
Quadrilaterals
IN THIS CHAPTER
![]() Crossing the road to get to the other side: Parallel lines and transversals
Crossing the road to get to the other side: Parallel lines and transversals
![]() Tracing the family tree of quadrilaterals
Tracing the family tree of quadrilaterals
![]() Plumbing the depths of parallelograms, rectangles, and rhombuses
Plumbing the depths of parallelograms, rectangles, and rhombuses
![]() Proving a figure is a parallelogram or other special quadrilateral
Proving a figure is a parallelogram or other special quadrilateral
In Chapters 4 and 5, you deal with three-sided polygons: triangles. In this chapter, you check out quadrilaterals, polygons with four sides. Then, in Chapter 7, you see polygons up to a gazillion sides. Totally exciting, right?
Parallel Line Properties
Most of the quadrilaterals you’ll deal with have parallel sides, so let’s begin with some info on parallel lines.
Parallel lines with a transversal
Check out Figure 6-1, which shows three lines that kind of resemble a giant not-equal sign. The two horizontal lines are parallel, and the third line that crosses them is called a transversal. As you can see, the three lines form eight angles.
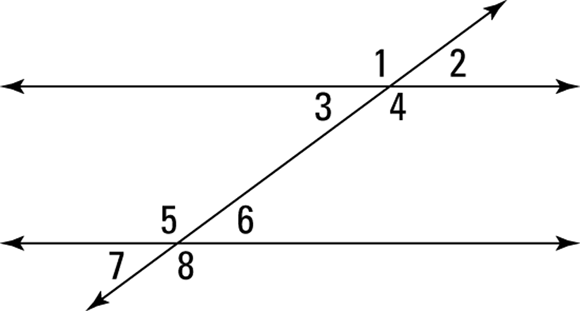
FIGURE 6-1: Two parallel lines, one transversal, and eight angles.
The eight angles formed by parallel lines and a transversal are either congruent or supplementary. The following theorems tell you how various pairs of angles relate to each other.
- Alternate interior angles: The pair of angles 3 and 6 (as well as 4 and 5) are alternate interior angles. These angle pairs are on opposite (alternate) sides of the transversal and are in between (in the interior of) the parallel lines.
- Alternate exterior angles: Angles 1 and 8 (and angles 2 and 7) are called alternate exterior angles.
- Corresponding angles: The pair of angles 1 and 5 (also 2 and 6, 3 and 7, and 4 and 8) are corresponding angles. Angles 1 and 5 are corresponding because each is in the same position (the upper left-hand corner) in its group of four angles.
- Same-side interior angles: Angles 3 and 5 (and 4 and 6) are on the same side of the transversal and are in the interior of the parallel lines, so they’re called (ready for a shock?) same-side interior angles.
- Same-side exterior angles: Angles 1 and 7 (and 2 and 8) are called same-side exterior angles.
- Two corresponding angles are congruent.
- Two alternate interior angles are congruent.
- Two alternate exterior angles are congruent.
- Two same-side interior angles are supplementary.
- Two same-side exterior angles are supplementary.
The transversal theorems
Let’s take a look at some of the theorems in action: Given that lines m and n are parallel, find the measure of ![]() .
.

The ![]() angle and the
angle and the ![]() angle are alternate exterior angles and are therefore congruent. Set them equal to each other and solve for x:
angle are alternate exterior angles and are therefore congruent. Set them equal to each other and solve for x:

This equation has two solutions, so take them one at a time and plug them into the x’s in the alternate exterior angles. Plugging ![]() into
into ![]() gives you
gives you ![]() for that angle. And because
for that angle. And because ![]() is its supplement,
is its supplement, ![]() must be
must be ![]() , or
, or ![]() . The
. The ![]() solution gives you
solution gives you ![]() for the
for the ![]() angle and
angle and ![]() for
for ![]() . So
. So ![]() and
and ![]() are your answers for
are your answers for ![]() .
.
Now here’s a proof that uses some of the transversal theorems:


For instance, if you have a hard time seeing that ![]() and
and ![]() are indeed alternate interior angles (for step 3 of the proof), rotate the figure (or tilt your head) until the parallel segments
are indeed alternate interior angles (for step 3 of the proof), rotate the figure (or tilt your head) until the parallel segments ![]() and
and ![]() are horizontal; then extend
are horizontal; then extend ![]() ,
,![]() , and
, and ![]() in both directions, turning them into lines (you know, with the little arrows). After doing that, you’re looking at the familiar parallel-line scheme shown in Figure 6-1.
in both directions, turning them into lines (you know, with the little arrows). After doing that, you’re looking at the familiar parallel-line scheme shown in Figure 6-1.
The Seven Special Quadrilaterals
In this section and the next, you find out about the seven quadrilaterals. Some are surely familiar to you, and some may not be so familiar. Check out the following definitions and the quadrilateral family tree in Figure 6-2.

FIGURE 6-2: The royal family tree of quadrilaterals.
If you know what the quadrilaterals look like, their definitions should make sense and be pretty easy to understand (though the first one is a bit of a mouthful).
- Kite: A quadrilateral in which two disjoint pairs of consecutive sides are congruent. (“Disjoint pairs” means that one side can’t be used in both pairs.)
- Parallelogram: A quadrilateral that has two pairs of parallel sides.
- Rhombus: A quadrilateral with four congruent sides. A rhombus is both a kite and a parallelogram.
- Rectangle: A quadrilateral with four right angles. A rectangle is a type of parallelogram.
- Square: A quadrilateral with four congruent sides and four right angles. A square is both a rhombus and a rectangle.
- Trapezoid: A quadrilateral with exactly one pair of parallel sides. (The parallel sides are called bases.)
- Isosceles trapezoid: A trapezoid in which the nonparallel sides (the legs) are congruent.
In the hierarchy of quadrilaterals shown in Figure 6-2, a quadrilateral below another on the family tree is a special case of the one above it. A rectangle, for example, is a special case of a parallelogram. Thus, you can say that a rectangle is a parallelogram but not that a parallelogram is a rectangle (because a parallelogram is only sometimes a rectangle).
Working with Auxiliary Lines
The following proof introduces you to a new idea: adding a line or segment (called an auxiliary line) to a proof diagram to help you do the proof.
Here’s an example proof. (For this proof to make sense, you’re not allowed to use the fact that opposite sides of a parallelogram are congruent; I get to that in the next section).

You might come up with a game plan like the following:
- Take a look at the givens. The only thing you can conclude from the single given is that the sides of GRAM are parallel (using the definition of a parallelogram). But it doesn’t seem like you can go anywhere from there.
- Jump to the end of the proof. What could be the justification for the final statement,
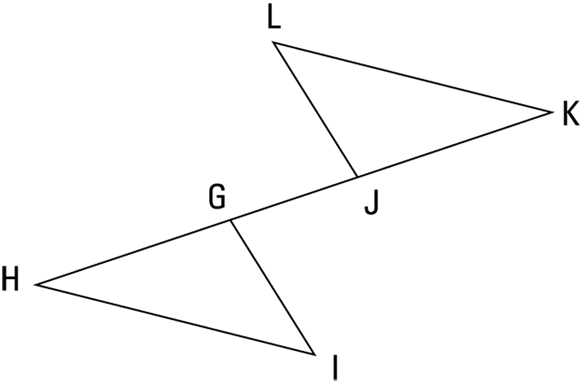
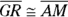 ? At this point, no justification seems possible, so put on your thinking cap.
? At this point, no justification seems possible, so put on your thinking cap. - Consider drawing an auxiliary line. If you draw
 , as shown in Figure 6-3, you get triangles that look congruent. And if you could show that they’re congruent, the proof could then end with CPCTC.
, as shown in Figure 6-3, you get triangles that look congruent. And if you could show that they’re congruent, the proof could then end with CPCTC. - Show the triangles congruent. To show that the triangles are congruent, you use
 as a transversal. First use it with parallel sides
as a transversal. First use it with parallel sides 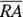 and
and 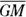 ; that gives you congruent, alternate interior angles GMR and ARM. Then use
; that gives you congruent, alternate interior angles GMR and ARM. Then use  with parallel sides
with parallel sides  and
and  ; that gives you two more congruent, alternate interior angles, GRM and AMR. These two pairs of congruent angles, along with side
; that gives you two more congruent, alternate interior angles, GRM and AMR. These two pairs of congruent angles, along with side  (which is congruent to itself by the Reflexive Property), prove the triangles congruent with ASA. That does it.
(which is congruent to itself by the Reflexive Property), prove the triangles congruent with ASA. That does it.

FIGURE 6-3: Connecting two points creates triangles you can use.


FIGURE 6-4: Four pairs of Z-angles.

FIGURE 6-5: The two pairs of Z-angles from the preceding proof — a backward Z and a tipped Z.
The Properties of Quadrilaterals
- Sides: Are they congruent? Parallel?
- Angles: Are they congruent? Supplementary? Right?
- Diagonals: Are they congruent? Perpendicular? Do they bisect each other? Do they bisect the angles whose vertices they meet?
I present a total of about 30 quadrilateral properties, which may seem like a lot to memorize. No worries. You don’t have to rely solely on memorization. Here’s a great tip that makes learning the properties a snap.
Properties of the parallelogram
- Opposite sides are parallel by definition.
- Opposite sides are congruent.
- Opposite angles are congruent.
- Consecutive angles are supplementary.
- The diagonals bisect each other.
If you just look at a parallelogram, the things that look true (namely, the things on this list) are true and are thus properties, and the things that don’t look like they’re true aren’t properties.
Imagine that you can’t remember the properties of a parallelogram. You could just sketch one (as in Figure 6-6) and run through all things that might be properties.

FIGURE 6-6: A run-of-the-mill parallelogram.
Tables 6-1, 6-2, and 6-3 concern questions about what might or might not be properties of a parallelogram (refer to Figure 6-6).
TABLE 6-1 Questions about Sides of Parallelograms
Do Any Sides Appear to Be … |
Answer |
Congruent? |
Yes, opposite sides look congruent, and that’s a property. But adjacent sides don’t look congruent, and that’s not a property. |
Parallel? |
Yes, opposite sides look parallel (and of course, you know this property if you know the definition of a parallelogram). |
TABLE 6-2 Questions about Angles of Parallelograms
Do Any Angles Appear to Be … |
Answer |
Congruent? |
Yes, opposite angles look congruent, and that’s a property. (Angles A and C appear to be about |
Supplementary? |
Yes, consecutive angles (like angles A and B) look like they’re supplementary, and that’s a property. |
Right angles? |
Obviously not, and that’s not a property. |
TABLE 6-3 Questions about Parallelogram Diagonals
Do the Diagonals Appear to Be … |
Answer |
Congruent? |
Not even close (in Figure 6-6, one is roughly twice as long as the other, which surprises most people; measure them if you don’t believe me!) — not a property. |
Perpendicular? |
Not even close; not a property. |
Bisecting each other? |
Yes, each one seems to cut the other in half, and that’s a property. |
Bisecting the angles whose vertices they meet? |
No. At a quick glance, you might think that |
The sketching-quadrilaterals method and the questions in the preceding three tables bring me to an important tip about mathematics in general.
Properties of the three special parallelograms
Figure 6-7 shows you the three special parallelograms, so-called because they’re, as mathematicians say, special cases of the parallelogram. (In addition, the square is a special case or type of both the rectangle and the rhombus.) The three-level hierarchy you see with parallelogram ![]() rectangle
rectangle ![]() square or parallelogram
square or parallelogram ![]() rhombus
rhombus ![]() square in the quadrilateral family tree (Figure 6-2) works just like mammal
square in the quadrilateral family tree (Figure 6-2) works just like mammal ![]() dog
dog ![]() Dalmatian. A dog is a special type of a mammal, and a Dalmatian is a special type of a dog.
Dalmatian. A dog is a special type of a mammal, and a Dalmatian is a special type of a dog.
FIGURE 6-7: The two kids and one grandkid (the square) of the parallelogram.
Before reading the properties that follow, try figuring them out on your own. Using the shapes in Figure 6-7, run down the list of possible properties from the beginning of “The Properties of Quadrilaterals,” asking yourself whether they look like they’re true for the rhombus, the rectangle, and the square.
- The rhombus has the following properties:
- All the properties of a parallelogram apply.
- All sides are congruent by definition.
- The diagonals bisect the angles.
- The diagonals are perpendicular bisectors of each other.
- The rectangle has the following properties:
- All the properties of a parallelogram apply.
- All angles are right angles by definition.
- The diagonals are congruent.
- The square has the following properties:
- All the properties of a rhombus apply.
- All the properties of a rectangle apply.
- All sides are congruent by definition.
- All angles are right angles by definition.
Let’s try a problem: Find the perimeter of rhombus RHOM.

Here’s the solution: All the sides of a rhombus are congruent, so HO equals ![]() . And because the diagonals of a rhombus are perpendicular,
. And because the diagonals of a rhombus are perpendicular, ![]() is a right triangle. You finish with the Pythagorean Theorem:
is a right triangle. You finish with the Pythagorean Theorem:

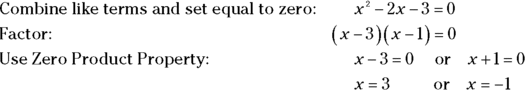
You can reject ![]() because that would result in
because that would result in ![]() having legs with lengths of
having legs with lengths of ![]() and 0. So x equals 3, which gives
and 0. So x equals 3, which gives ![]() a length of 5. Because rhombuses have four congruent sides, RHOM has a perimeter of
a length of 5. Because rhombuses have four congruent sides, RHOM has a perimeter of ![]() , or 20 units.
, or 20 units.
Properties of the kite
Check out the kite in Figure 6-8 and try to figure out its properties before reading the list that follows.

FIGURE 6-8: A mathematical kite that looks ready for flying.
- Two disjoint pairs of consecutive sides are congruent by definition (
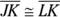 and
and 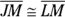 ). Note: Disjoint means that one side can’t be used in both pairs — the two pairs are totally separate.
). Note: Disjoint means that one side can’t be used in both pairs — the two pairs are totally separate. - The diagonals are perpendicular.
- One diagonal (
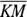 , the main diagonal) is the perpendicular bisector of the other diagonal (
, the main diagonal) is the perpendicular bisector of the other diagonal ( , the cross diagonal). (The terms “main diagonal” and “cross diagonal” are quite useful, but don’t look for them in other geometry books because I made them up.)
, the cross diagonal). (The terms “main diagonal” and “cross diagonal” are quite useful, but don’t look for them in other geometry books because I made them up.) - The main diagonal bisects a pair of opposite angles (
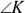 and
and  ).
). - The opposite angles at the endpoints of the cross diagonal are congruent (
 and
and  ).
).
The last three properties are called the half properties of the kite.
Grab an energy drink and get ready for another proof. Due to space considerations, I’m going to skip the game plan this time. You’re on your own — egad!



Properties of the trapezoid and the isosceles trapezoid
- The properties of the trapezoid are as follows:
- The bases are parallel by definition.
- Each lower base angle is supplementary to the upper base angle on the same side.
- The properties of the isosceles trapezoids are as follows:
- The properties of trapezoids apply by definition.
- The legs are congruent by definition.
- The lower base angles are congruent.
- The upper base angles are congruent.
- Any lower base angle is supplementary to any upper base angle.
- The diagonals are congruent.

FIGURE 6-9: A trapezoid (on the left) and an isosceles trapezoid (on the right).
Proving That You’ve Got a Particular Quadrilateral
The last two sections told you all about seven different quadrilaterals — their definitions, their properties, what they look like, and where they fit on the family tree. Here, I fill you in on proving that a given quadrilateral qualifies as one of those particular types.
Proving you’ve got a parallelogram
The five methods for proving that a quadrilateral is a parallelogram are among the most important proof methods in this section. One reason they’re important is that you often have to prove that a quadrilateral is a parallelogram before going on to prove that it’s one of the special parallelograms (a rectangle, a rhombus, or a square).
- If both pairs of opposite sides of a quadrilateral are parallel, then it’s a parallelogram (reverse of the parallelogram definition).
- If both pairs of opposite sides of a quadrilateral are congruent, then it’s a parallelogram.
- If both pairs of opposite angles of a quadrilateral are congruent, then it’s a parallelogram.
- If the diagonals of a quadrilateral bisect each other, then it’s a parallelogram.
- If one pair of opposite sides of a quadrilateral are both parallel and congruent, then it’s a parallelogram.
Here’s a proof to give you some practice with one of the parallelogram proof methods.
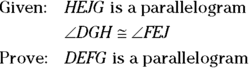

Your game plan might go something like this:
- Look for congruent triangles. This diagram takes the cake for containing congruent triangles — it has six pairs of them! Don’t spend much time thinking about them — except the ones that might help you — but at least make a quick mental note that they’re there.
- Consider the givens. The given congruent angles, which are parts of
 and
and  , are a huge hint that you should try to show these triangles congruent. You have those congruent angles and the congruent sides
, are a huge hint that you should try to show these triangles congruent. You have those congruent angles and the congruent sides  and
and  from parallelogram HEJG so you need only one more pair of congruent sides or angles to use SAS or ASA.
from parallelogram HEJG so you need only one more pair of congruent sides or angles to use SAS or ASA. Think about the end of the proof. To prove that DEFG is a parallelogram, it would help to know that
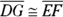 so you’d like to be able to prove the triangles congruent and then get
so you’d like to be able to prove the triangles congruent and then get  by CPCTC. That eliminates the SAS option for proving the triangles congruent because to use SAS, you’d need to know that
by CPCTC. That eliminates the SAS option for proving the triangles congruent because to use SAS, you’d need to know that  — the very thing you’re trying to get with CPCTC. (And if you knew
— the very thing you’re trying to get with CPCTC. (And if you knew 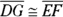 there’d be no point to showing that the triangles are congruent, anyway.) So you should try the other option: proving the triangles congruent with ASA.
there’d be no point to showing that the triangles are congruent, anyway.) So you should try the other option: proving the triangles congruent with ASA.The second angle pair you’d need for ASA consists of
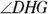 and
and 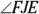 . They’re congruent because they’re alternate exterior angles using parallel lines
. They’re congruent because they’re alternate exterior angles using parallel lines  and
and  and transversal
and transversal  . Okay, so the triangles are congruent by ASA, and then you get
. Okay, so the triangles are congruent by ASA, and then you get  by CPCTC. You’re on your way.
by CPCTC. You’re on your way.Consider parallelogram proof methods. You now have one pair of congruent sides of DEFG. Two of the parallelogram proof methods use a pair of congruent sides. To complete one or the other of these methods, you need to show one of the following:
- That the other pair of opposite sides are congruent
- That
 and
and 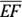 are parallel as well as congruent
are parallel as well as congruent
Ask yourself which approach looks easier or quicker. Showing
 would probably require showing a second pair of triangles congruent, and that looks like it’d take a few more steps, so try the other tack.
would probably require showing a second pair of triangles congruent, and that looks like it’d take a few more steps, so try the other tack.Can you show
 ? Sure, with one of the parallel-line theorems. Because angles GDH and EFJ are congruent (by CPCTC), you can finish by using those angles as congruent alternate interior angles, or Z-angles, to give you
? Sure, with one of the parallel-line theorems. Because angles GDH and EFJ are congruent (by CPCTC), you can finish by using those angles as congruent alternate interior angles, or Z-angles, to give you  . That’s a wrap!
. That’s a wrap!
Now take a look at the formal proof:

Proving that you’ve got a rectangle, rhombus, or square
- If all angles in a quadrilateral are right angles, then it’s a rectangle (reverse of the rectangle definition).
- If the diagonals of a parallelogram are congruent, then it’s a rectangle.
- If a parallelogram contains a right angle, then it’s a rectangle.
- If all sides of a quadrilateral are congruent, then it’s a rhombus (reverse of the rhombus definition).
- If the diagonals of a quadrilateral bisect all the angles, then it’s a rhombus.
- If the diagonals of a quadrilateral are perpendicular bisectors of each other, then it’s a rhombus.
- If two consecutive sides of a parallelogram are congruent, then it’s a rhombus.
- If either diagonal of a parallelogram bisects two angles, then it’s a rhombus.
- If the diagonals of a parallelogram are perpendicular, then it’s a rhombus.
- If a quadrilateral has four congruent sides and four right angles, then it’s a square (reverse of the square definition).
- If two consecutive sides of a rectangle are congruent, then it’s a square.
- If a rhombus contains a right angle, then it’s a square.
- If a quadrilateral is both a rectangle and a rhombus, then it’s a square.
Proving that you’ve got a kite
- If two disjoint pairs of consecutive sides of a quadrilateral are congruent, then it’s a kite (reverse of the kite definition).
- If one of the diagonals of a quadrilateral is the perpendicular bisector of the other, then it’s a kite.
- Check the diagram for congruent triangles. Don’t fail to spot triangles that look congruent and to consider how using CPCTC might help you.
- Keep the first equidistance theorem in mind. When you have to prove that a quadrilateral is a kite, you might have to use the equidistance theorem in which two points determine a perpendicular bisector.
- Draw in diagonals. One of the methods for proving that a quadrilateral is a kite involves diagonals, so if the diagram lacks either of the two diagonals, try drawing in one or both of them.
Now get ready for a proof:
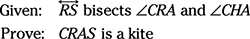

Here’s how your game plan might work for this proof.
- Note that one of the kite’s diagonals is missing. Draw in the missing diagonal,
 .
. - Check the diagram for congruent triangles. After drawing in
 , there are six pairs of congruent triangles. The two triangles most likely to help you are
, there are six pairs of congruent triangles. The two triangles most likely to help you are 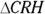 and
and  .
. - Prove the triangles congruent. You can use ASA.
- Use the equidistance theorem. Use CPCTC with
 and
and  to get
to get 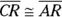 and
and 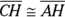 . Then, using the equidistance theorem, those two pairs of congruent sides (with points R and H) determine the perpendicular bisector of the diagonal you drew in. Over and out.
. Then, using the equidistance theorem, those two pairs of congruent sides (with points R and H) determine the perpendicular bisector of the diagonal you drew in. Over and out.
I’m skipping the formal proof, but give it a try. It should take you about 12 steps.

 Proving that angles are congruent: If a transversal intersects two parallel lines, then the following angles are congruent:
Proving that angles are congruent: If a transversal intersects two parallel lines, then the following angles are congruent:  You can sum up the definitions and theorems above with the following simple idea. When you have two parallel lines cut by a transversal, you get four acute angles and four obtuse angles (except when you get eight right angles). All the acute angles are congruent, all the obtuse angles are congruent, and each acute angle is supplementary to each obtuse angle.
You can sum up the definitions and theorems above with the following simple idea. When you have two parallel lines cut by a transversal, you get four acute angles and four obtuse angles (except when you get eight right angles). All the acute angles are congruent, all the obtuse angles are congruent, and each acute angle is supplementary to each obtuse angle. When you get two solutions (such as
When you get two solutions (such as  The properties of the quadrilaterals are simply the things that are true about them. The properties of a particular quadrilateral concern its
The properties of the quadrilaterals are simply the things that are true about them. The properties of a particular quadrilateral concern its