Chapter 7
Polygon Formulas
IN THIS CHAPTER
![]() Finding the area of quadrilaterals
Finding the area of quadrilaterals
![]() Computing the area of regular polygons
Computing the area of regular polygons
![]() Determining the number of diagonals in a polygon
Determining the number of diagonals in a polygon
![]() Heating things up with the number of degrees in a polygon
Heating things up with the number of degrees in a polygon
In this chapter, you take a break from proofs and move on to problems that have a little more to do with the real world. I emphasize little because the shapes you deal with here — such as trapezoids, hexagons, octagons, and yep, even pentadecagons (15 sides) — aren’t exactly things you encounter outside of math class on a regular basis. But at least the concepts you work with here — the length and size and shape of polygons — are fairly ordinary things. For nearly everyone, relating to visual, real-world things like this is easier than relating to proofs, which are more in the realm of pure mathematics.
The Area of Quadrilaterals
I’m sure you’ve had to calculate the area of a square or rectangle before, whether it was in a math class or in some more practical situation, such as when you wanted to know the area of a room in your house. In this section, you see the square and rectangle formulas again, and you also get some new, gnarlier formulas you may not have seen before.
Quadrilateral area formulas
Here are the five area formulas for the seven special quadrilaterals. There are only five formulas because some of them do double duty — for example, you can calculate the area of a rhombus with the kite formula.

 (because a rhombus is a type of parallelogram, you can use this formula for a rhombus)
(because a rhombus is a type of parallelogram, you can use this formula for a rhombus)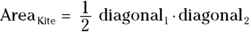 , or
, or 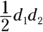 (a rhombus is also a type of kite, so you can use this formula for a rhombus as well)
(a rhombus is also a type of kite, so you can use this formula for a rhombus as well) , or
, or  (this second formula works because a square is a type of kite)
(this second formula works because a square is a type of kite)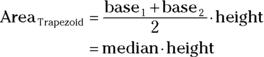
Note: The median of a trapezoid is the segment that connects the midpoints of the legs. Its length equals the average of the lengths of the bases.
Why the formulas work
- Parallelogram: In Figure 7-1, if you cut off the little triangle on the left and fill it in on the right, the parallelogram becomes a rectangle (and the area obviously hasn’t changed). This rectangle has the same base and height as the original parallelogram. The area of the rectangle is
 , so that formula gives you the area of the parallelogram as well. If you don’t believe me (even though you should by now) you can try this yourself by cutting out a paper parallelogram and snipping off the triangle, as shown in Figure 7-1.
, so that formula gives you the area of the parallelogram as well. If you don’t believe me (even though you should by now) you can try this yourself by cutting out a paper parallelogram and snipping off the triangle, as shown in Figure 7-1. - Kite: Figure 7-2 shows that the kite has half the area of the rectangle drawn around it (this follows from the fact that
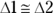 ,
,  , and so on). You can see that the length and width of the large rectangle are the same as the lengths of the diagonals of the kite. The area of the rectangle
, and so on). You can see that the length and width of the large rectangle are the same as the lengths of the diagonals of the kite. The area of the rectangle 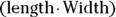 thus equals
thus equals  , and because the kite has half that area, its area is
, and because the kite has half that area, its area is  .
. - Trapezoid: If you cut off the two triangles and move them as I show you in Figure 7-3, the trapezoid becomes a rectangle. This rectangle has the same height as the trapezoid, and its base equals the median (m) of the trapezoid. Thus, the area of the rectangle (and therefore the trapezoid as well) equals
 .
.

FIGURE 7-1: The relationship between a parallelogram and a rectangle.
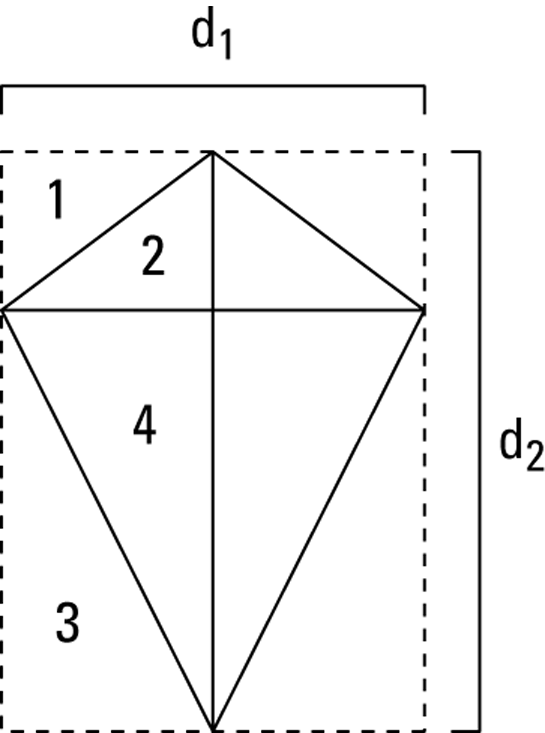
FIGURE 7-2: The kite takes up half of each of the four small rectangles and thus is half the area of the large rectangle.

FIGURE 7-3: The relationship between a trapezoid and a rectangle.
Trying a few area problems
Locating special right triangles in parallelograms
Find the area of parallelogram ABCD in Figure 7-4.

FIGURE 7-4: Use a 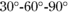 triangle to find the area of this parallelogram.
triangle to find the area of this parallelogram.
To get started, draw in the height of the parallelogram straight down from B to base ![]() to form a right triangle, as shown in Figure 7-5.
to form a right triangle, as shown in Figure 7-5.

FIGURE 7-5: Drawing in the height creates a right triangle.
Consecutive angles in a parallelogram are supplementary. Angle ABC is ![]() , so
, so ![]() is
is ![]() , and
, and ![]() is thus a
is thus a ![]() triangle. Now, if you know the ratio of the lengths of the sides in a
triangle. Now, if you know the ratio of the lengths of the sides in a ![]() triangle,
triangle, ![]() , the rest is a snap.
, the rest is a snap. ![]() (the 2x side) equals
(the 2x side) equals ![]() and is thus 6. Then
and is thus 6. Then ![]() (the x side) is half of that, or 3;
(the x side) is half of that, or 3; ![]() (the
(the ![]() side) is therefore
side) is therefore ![]() . Here’s the finish with the area formula:
. Here’s the finish with the area formula:

Using triangles and ratios in a rhombus problem
Now for a rhombus problem: Find the area of rhombus RHOM given that ![]() is 6 and that the ratio of
is 6 and that the ratio of ![]() to
to ![]() is 4 : 1 (see Figure 7-6).
is 4 : 1 (see Figure 7-6).

FIGURE 7-6: Find the area of this rhombus.
This one’s a bit tricky. You might feel that you’re not given enough information to solve it or that you just don’t know how to begin. If you ever feel this way when you’re in the middle of a problem, I have a great tip for you.
Because the ratio of ![]() to
to ![]() is 4 : 1, you can give
is 4 : 1, you can give ![]() a length of 4x and
a length of 4x and ![]() a length of x.
a length of x. ![]() is thus
is thus ![]() , or 5x, and so is
, or 5x, and so is ![]() , because all sides of a rhombus are congruent. Now you have a right triangle
, because all sides of a rhombus are congruent. Now you have a right triangle ![]() with legs of 4x and 6 and a hypotenuse of 5x, so you can use the Pythagorean Theorem:
with legs of 4x and 6 and a hypotenuse of 5x, so you can use the Pythagorean Theorem:
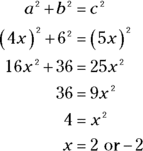
Because side lengths must be positive, you reject the answer ![]() . The length of the base,
. The length of the base, ![]() , is thus 5(2), or 10. (Triangle RBM is your old, familiar friend, a 3-4-5 triangle blown up by a factor of 2.) Now use the parallelogram-rhombus area formula:
, is thus 5(2), or 10. (Triangle RBM is your old, familiar friend, a 3-4-5 triangle blown up by a factor of 2.) Now use the parallelogram-rhombus area formula:
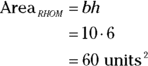
Drawing in diagonals to find a kite’s area
What’s the area of kite KITE in Figure 7-7?

FIGURE 7-7: A kite with a funky side length.
So draw in ![]() and
and ![]() . Use “X” for the point where the diagonals cross. Use some scratch paper, or draw on Figure 7-7; no one will know.
. Use “X” for the point where the diagonals cross. Use some scratch paper, or draw on Figure 7-7; no one will know.
Triangle KIT is a right triangle with congruent legs, so it’s a ![]() triangle with sides in the ratio of
triangle with sides in the ratio of ![]() . The length of the hypotenuse,
. The length of the hypotenuse, ![]() , thus equals one of the legs times
, thus equals one of the legs times ![]() ; that’s
; that’s ![]() , or 16.
, or 16. ![]() is half of that, or 8.
is half of that, or 8.
Triangle KIX is another ![]() triangle (
triangle (![]() ), the kite’s main diagonal, bisects opposite angles KIT and KET, and half of
), the kite’s main diagonal, bisects opposite angles KIT and KET, and half of ![]() is
is ![]() ; therefore,
; therefore, ![]() , like
, like ![]() , is 8. You’ve got another right triangle,
, is 8. You’ve got another right triangle, ![]() , with a side of 8 and a hypotenuse of 17. I hope that rings a bell! You’re looking at an 8-15-17 triangle, so without any work, you see that
, with a side of 8 and a hypotenuse of 17. I hope that rings a bell! You’re looking at an 8-15-17 triangle, so without any work, you see that ![]() is 15. (No bells? No worries. You can get
is 15. (No bells? No worries. You can get ![]() with the Pythagorean Theorem instead.) Add
with the Pythagorean Theorem instead.) Add ![]() to
to ![]() and you get
and you get ![]() for diagonal
for diagonal ![]() .
.
Now that you know the diagonal lengths, you have what you need to finish. The length of diagonal ![]() is 16, and diagonal
is 16, and diagonal ![]() is 23. Plug these numbers into the kite area formula for your final answer:
is 23. Plug these numbers into the kite area formula for your final answer:
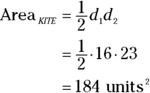
The Area of Regular Polygons
In case you’ve been dying to know how to figure the area of your ordinary, octagonal stop sign, you’ve come to the right place. In this section, you discover how to find the area of equilateral triangles and other regular polygons.
The polygon area formulas
A regular polygon is equilateral (it has equal sides) and equiangular (it has equal angles). To find the area of a regular polygon, you use an apothem — a segment that joins the polygon’s center to the midpoint of any side and that is perpendicular to that side. (![]() in upcoming Figure 7-8 is an apothem.)
in upcoming Figure 7-8 is an apothem.)
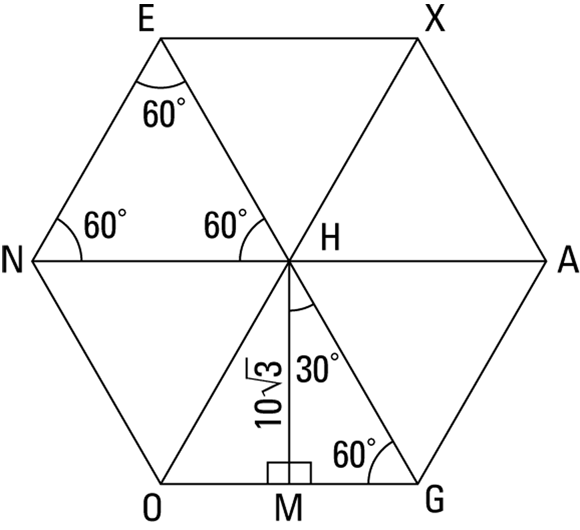
FIGURE 7-8: A regular hexagon cut into six congruent, equilateral triangles.
Note: This formula is usually written as ![]() , but if I do say so myself, the way I’ve written it,
, but if I do say so myself, the way I’ve written it, ![]() , is better. I like this way of writing it because the formula is based on the triangle area formula,
, is better. I like this way of writing it because the formula is based on the triangle area formula, ![]() : The polygon’s perimeter (p) is related to the triangle’s base (b), and the apothem (a) is related to the height (h).
: The polygon’s perimeter (p) is related to the triangle’s base (b), and the apothem (a) is related to the height (h).
An equilateral triangle is the regular polygon with the fewest possible number of sides. To figure its area, you can use the regular polygon formula; however, it also has its own area formula.
(where s is the length of each of the triangle’s sides)
Tackling an area problem
Don’t tell me about your problems; I’ve got problems of my own — and here’s one of them.
What’s the area of a regular hexagon with an apothem of ![]() ?
?
First, sketch the hexagon with its three diagonals, creating six equilateral triangles. Then draw in an apothem, which goes from the center to the midpoint of a side. Figure 7-8 shows hexagon EXAGON.
Note that the apothem divides ![]() into two
into two ![]() triangles (halves of an equilateral triangle). The apothem is the long leg (the
triangles (halves of an equilateral triangle). The apothem is the long leg (the ![]() side) of a
side) of a ![]() triangle, so
triangle, so
![]() is the short leg (the x side), so its length is 10.
is the short leg (the x side), so its length is 10. ![]() is twice as long, so it’s 20. And the perimeter is six times that, or 120.
is twice as long, so it’s 20. And the perimeter is six times that, or 120.
Now you can finish with either the regular polygon formula or the equilateral triangle formula (multiplied by 6). They’re equally easy. Take your pick. Here’s what it looks like with the regular polygon formula:

Angle and Diagonal Formulas
In this section, you get polygon formulas involving — hold onto your hat — angles and diagonals!
Interior and exterior angles
You use two kinds of angles when working with polygons (see Figure 7-9):
- Interior angle: An interior angle of a polygon is an angle inside the polygon at one of its vertices. Angle Q is an interior angle of quadrilateral QUAD.
- Exterior angle: An exterior angle of a polygon is an angle outside the polygon formed by one of its sides and the extension of an adjacent side. Angle ADZ,
 , and
, and 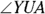 are exterior angles of QUAD; vertical angle
are exterior angles of QUAD; vertical angle  is not an exterior angle of QUAD.
is not an exterior angle of QUAD.
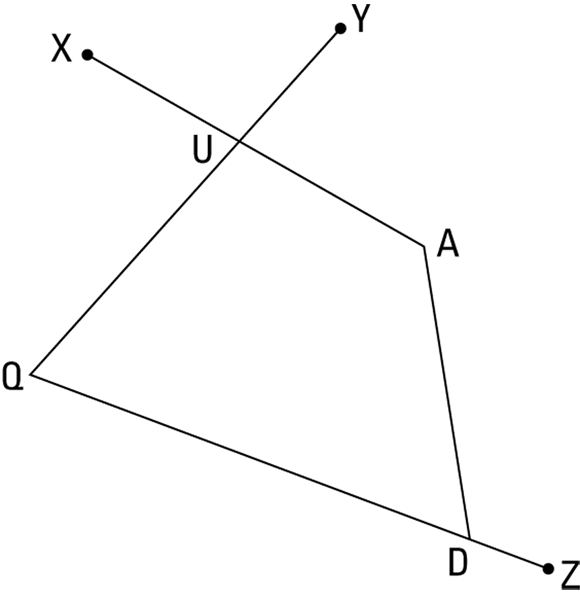
FIGURE 7-9: Interior and exterior angles.
- The sum of the measures of the interior angles of a polygon with n sides is
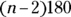 .
. - The measure of each interior angle of an equiangular n-gon is
 (the supplement of an exterior angle).
(the supplement of an exterior angle). - If you count one exterior angle at each vertex, the sum of the measures of the exterior angles of a polygon is
 .
. - The measure of each exterior angle of an equiangular n-gon is
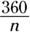 .
.
A polygon angle problem
You can practice the interior and exterior angle formulas in the following three-part problem: Given a regular dodecagon (12 sides),
Find the sum of the measures of its interior angles.
Just plug the number of sides (12) into the formula for the sum of the interior angles of a polygon:

Find the measure of a single interior angle.
This polygon has 12 sides, so it has 12 angles; and because you’re dealing with a regular polygon, all its angles are congruent. So to find the measure of a single angle, just divide your answer from the first part of the problem by 12. (Note that this is basically the same as using the first formula for a single interior angle.)

Find the measure of a single exterior angle with the exterior angle formula; then check that its supplement, an interior angle, equals the answer you got from part 2 of the problem.
First, plug 12 into the oh-so-simple exterior angle formula:

Now take the supplement of your answer to find the measure of a single interior angle, and check that it’s the same as your answer from part 2:

It checks. (And note that this final computation is basically the same thing as using the second formula for a single interior angle.)
Criss-crossing with diagonals
Here’s one last problem for you: If a polygon has 90 diagonals, how many sides does it have?
You know what the formula for the number of diagonals in a polygon is, and you know that the polygon has 90 diagonals, so plug 90 in for the answer and solve for n:
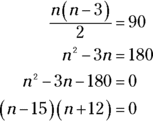
Thus, n equals 15 or ![]() . But because a polygon can’t have a negative number of sides, n must be 15. So you have a 15-sided polygon (a pentadecagon, in case you’re curious).
. But because a polygon can’t have a negative number of sides, n must be 15. So you have a 15-sided polygon (a pentadecagon, in case you’re curious).

 Quadrilateral area formulas:
Quadrilateral area formulas:  The area formulas for the parallelogram, kite, and trapezoid are based on the area of a rectangle. The following figures show you how each of these three quadrilaterals relates to a rectangle, and the following list gives you the details:
The area formulas for the parallelogram, kite, and trapezoid are based on the area of a rectangle. The following figures show you how each of these three quadrilaterals relates to a rectangle, and the following list gives you the details: