Chapter 10
3-D Geometry
IN THIS CHAPTER
![]() Flat-top solids: The prism and the cylinder
Flat-top solids: The prism and the cylinder
![]() Pointy-top solids: The pyramid and the cone
Pointy-top solids: The pyramid and the cone
![]() Top-less solids: Spheres
Top-less solids: Spheres
In this chapter, you study cones, spheres, prisms, and other solids of varying shapes, focusing on their two most fundamental characteristics, namely volume and surface area.
Flat-Top Figures
Flat-top figures (that’s what I call them, anyway) are solids with two congruent, parallel bases (the top and bottom). A prism — your standard cereal box is one example — has polygon-shaped bases, and a cylinder — like your standard soup can — has round bases. See Figure 10-1. But despite the different shape of their bases, the same volume and surface area formulas work for both of them because they share the flat-top structure.
- Prism: A prism is a solid figure with two congruent, parallel, polygonal bases. Its corners are called vertices, the segments that connect the vertices are called edges, and the flat sides are called faces.
- Cylinder: A cylinder is a solid figure with two congruent, parallel bases that have rounded sides (in other words, the bases are not straight-sided polygons); these bases are connected by a rounded surface.
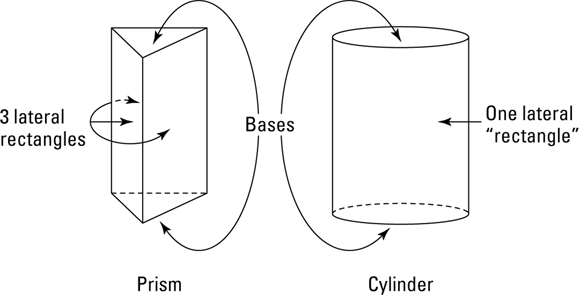
FIGURE 10-1: A prism and a cylinder with their bases and lateral rectangles.
Now that you know what these things are, here are their volume and surface area formulas.
An ordinary box is a special case of a prism, so you can use the flat-top volume formula for a box, but you probably already know the other way to compute a box’s volume: ![]() . (Because the length times the width gives you the area of the base, these two methods really amount to the same thing.) To get the volume of a cube, the simplest type of box, you just take the length of one of its edges (sides) and raise it to the third power
. (Because the length times the width gives you the area of the base, these two methods really amount to the same thing.) To get the volume of a cube, the simplest type of box, you just take the length of one of its edges (sides) and raise it to the third power ![]() .
.
Because prisms and cylinders have two congruent bases, you simply find the area of one base and double that value; then you add the figure’s lateral area. The lateral area of a prism or cylinder is the area of the sides of the figure — namely, the area of everything but the figure’s bases. Here’s how the two figures compare:
- The lateral area of a prism is made up of rectangles. The bases of a prism can be any shape, but the lateral area is always made up of rectangles. So to get the lateral area, you just find the area of the rectangles using the standard rectangle area formula and then add them up.
- The lateral area of a cylinder is basically one rectangle rolled into a tube shape. Think of the lateral area of a cylinder as one rectangular paper towel that rolls exactly once around a paper towel roll. The base of this rectangle (you know, the part of the towel that wraps around the bottom of the roll) is the same as the circumference of the cylinder’s base. And the height of the paper towel rectangle is the same as the height of the cylinder. So, the lateral area of a cylinder (the area of this rectangle) is
 , namely
, namely 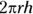 , or
, or 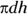 .
.
Time to take a look at some of these formulas in action.


Find the volume of the prism.
To use the volume formula, you need the prism’s height (
 ) and the area of its base (
) and the area of its base ( ). You’ve probably noticed that this prism is lying on its side. That’s why its height isn’t vertical and its base isn’t on the bottom.
). You’ve probably noticed that this prism is lying on its side. That’s why its height isn’t vertical and its base isn’t on the bottom.Get the height first. ABCD is a square, so
 (half of the square) is a
(half of the square) is a 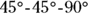 triangle with a hypotenuse of 8. To get the leg of a
triangle with a hypotenuse of 8. To get the leg of a 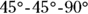 triangle, you divide the hypotenuse by
triangle, you divide the hypotenuse by 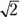 (or use the Pythagorean Theorem, noting that
(or use the Pythagorean Theorem, noting that 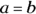 in this case). So that gives you
in this case). So that gives you  for the length of
for the length of 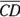 , which, again, is the height of the prism.
, which, again, is the height of the prism.And here’s how you get the area of
 : First, note that AD, like CD, is
: First, note that AD, like CD, is 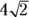 (because ABCD is a square). Next, because
(because ABCD is a square). Next, because  and
and  are given
are given  angles,
angles,  must be
must be  ; thus,
; thus,  is another
is another  triangle. Its hypotenuse,
triangle. Its hypotenuse, 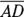 , has a length of
, has a length of  , so its legs (
, so its legs ( and
and  ) are
) are  , or 4 units long. The area of a right triangle is given by half the product of its legs (because you can use one leg for the triangle’s base and the other for its height), so
, or 4 units long. The area of a right triangle is given by half the product of its legs (because you can use one leg for the triangle’s base and the other for its height), so 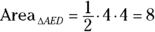 . You’re all set to finish with the volume formula:
. You’re all set to finish with the volume formula: 
Find the surface area of the prism.
Having completed part 1, you have everything you need to compute the surface area. Just plug in the numbers:

Pointy-Top Figures
What I call pointy-top figures are solids with one flat base and … a pointy top! The pointy-top solids are the pyramid and the cone. Even though the pyramid has a polygon-shaped base and the cone has a rounded base, the same volume and surface area formulas work for both.
- Pyramid: A pyramid is a solid figure with a polygonal base and edges that extend up from the base to meet at a single point.
- Cone: A cone is a solid figure with a rounded base and a rounded lateral surface that connects the base to a single point.
The lateral area of a pointy-top figure is the area of the surface that connects the base to the peak (it’s the area of everything but the base). Here’s what this means for pyramids and cones:
- The lateral area of a pyramid is made up of triangles. Each lateral triangle has an area of
 . But you can’t use the height of the pyramid for the height of its triangular faces, because the height of the pyramid doesn’t run along its faces. So instead, you use the pyramid’s slant height, which is just the ordinary altitude of the triangular faces. (The cursive letter
. But you can’t use the height of the pyramid for the height of its triangular faces, because the height of the pyramid doesn’t run along its faces. So instead, you use the pyramid’s slant height, which is just the ordinary altitude of the triangular faces. (The cursive letter  indicates the slant height.) Figure 10-2 shows how height and slant height differ.
indicates the slant height.) Figure 10-2 shows how height and slant height differ. - The lateral area of a cone is basically one triangle rolled into a cone shape. The lateral area of a cone is one “triangle” that’s been rolled into a cone shape like a snow-cone cup. (It’s only sort of a triangle because when flattened out, it’s actually a sector of a circle with a curved bottom side.) Its area is
 , just like one of the lateral triangles in a pyramid. The base of this “triangle” equals the circumference of the cone. So, the lateral area of a cone equals
, just like one of the lateral triangles in a pyramid. The base of this “triangle” equals the circumference of the cone. So, the lateral area of a cone equals 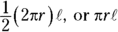 .
.

FIGURE 10-2: A pyramid and a cone with their heights and slant heights.

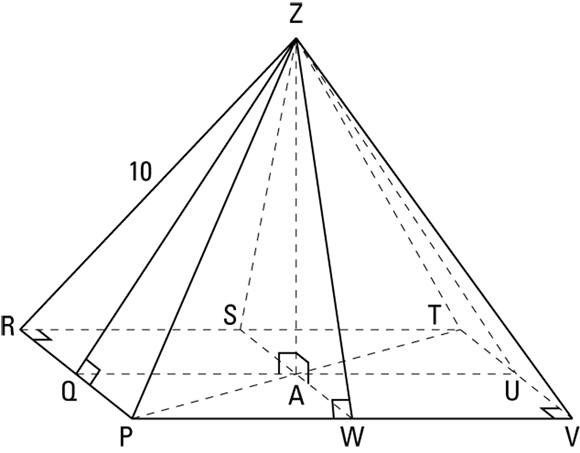
Find the pyramid’s volume.
To compute the volume of a pyramid, you need its height (
 ) and the area of its square base, PRTV. You can get the height by solving right triangle
) and the area of its square base, PRTV. You can get the height by solving right triangle  . The lateral edges of a pyramid are congruent; thus, the hypotenuse of
. The lateral edges of a pyramid are congruent; thus, the hypotenuse of  ,
, 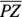 , is congruent to
, is congruent to  , and so its length is also 10.
, and so its length is also 10.  is half of the diagonal of the base, so it’s 6. Triangle PZA is thus a 3-4-5 triangle blown up to twice its size, namely a 6-8-10 triangle, so the height,
is half of the diagonal of the base, so it’s 6. Triangle PZA is thus a 3-4-5 triangle blown up to twice its size, namely a 6-8-10 triangle, so the height, 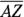 , is 8 (or you can use the Pythagorean Theorem to get
, is 8 (or you can use the Pythagorean Theorem to get  ).
).To get the area of square PRTV, you can, of course, first figure the length of its sides; but don’t forget that a square is a kite, so you can use the kite area formula instead — that’s the quickest way to get the area of a square if you know the length of a diagonal. Because the diagonals of a square are equal, both of them are 12, and you have what you need to use the kite area formula:

Now use the pointy-top volume formula:
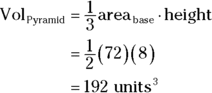
Find the pyramid’s surface area.
To use the pyramid surface area formula, you need the area of the base (which you got in part 1 of the problem) and the area of the triangular faces. To get the faces, you need the slant height,
 .
.First, solve
 . It’s a
. It’s a 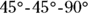 triangle with a hypotenuse (
triangle with a hypotenuse ( ) that’s 6 units long; to get the legs, you divide the hypotenuse by
) that’s 6 units long; to get the legs, you divide the hypotenuse by  (or use the Pythagorean Theorem).
(or use the Pythagorean Theorem). 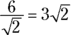 , so
, so 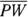 and
and  both have a length of
both have a length of 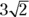 . Now you can get
. Now you can get  by using the Pythagorean Theorem with either of two right triangles,
by using the Pythagorean Theorem with either of two right triangles, 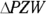 or
or 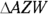 . Take your pick. How about
. Take your pick. How about  ?
? 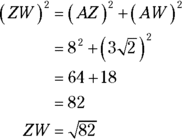
Now you’re all set to finish with the surface area formula. (One last fact you need is that
 is
is  because, of course, it’s twice as long as
because, of course, it’s twice as long as  .)
.) 


Find the cone’s volume.
To compute the cone’s volume, you need its height and the radius of its base. The radius is, of course, half the diameter, so it’s
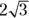 . Then, because the height is perpendicular to the base, the triangle formed by the radius, the height, and the slant height is a
. Then, because the height is perpendicular to the base, the triangle formed by the radius, the height, and the slant height is a  triangle. You can see that h is the long leg and r the short leg, so to get h, you multiply r by
triangle. You can see that h is the long leg and r the short leg, so to get h, you multiply r by 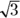 :
: 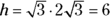
You’re ready to use the cone volume formula:
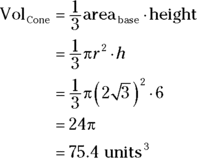
Find the cone’s surface area.
For the surface area, the only other thing you need is the slant height,
 . The slant height is the hypotenuse of the
. The slant height is the hypotenuse of the  triangle, so it’s just twice the radius, which makes it
triangle, so it’s just twice the radius, which makes it 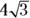 . Now plug everything into the cone surface area formula:
. Now plug everything into the cone surface area formula: 
Spheres
Have a ball with the following sphere problem: What’s the volume of a basketball in a box (a cube, of course) if the box has a surface area of ![]() ?
?

A cube (or any other ordinary box shape) is a special case of a prism, but you don’t need to use the fancy-schmancy prism formula, because the surface area of a cube is simply made up of six congruent squares. Call the length of an edge of the cube s. The area of each side is therefore ![]() . The cube has six faces, so its surface area is
. The cube has six faces, so its surface area is ![]() . Set this equal to the given surface area of
. Set this equal to the given surface area of ![]() and solve for s:
and solve for s:
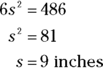
Thus, the edges of the cube are 9 inches, and because the basketball has the same width as the box it comes in, the diameter of the ball is also 9 inches; its radius is half of that, or 4.5 inches. Now you can finish by plugging 4.5 into the volume formula:

(By the way, this is slightly more than half the volume of the box, which is ![]() , or
, or ![]() .)
.)

 Volume of flat-top figures: The volume of a prism or cylinder is given by the following formula.
Volume of flat-top figures: The volume of a prism or cylinder is given by the following formula.  The key to pyramid problems about volume and surface area is right triangles. Find them and then solve them with the Pythagorean Theorem or by using your knowledge of special right triangles.
The key to pyramid problems about volume and surface area is right triangles. Find them and then solve them with the Pythagorean Theorem or by using your knowledge of special right triangles.