Chapter 4
Triangle Fundamentals
IN THIS CHAPTER
![]() Classifying triangles by their angles
Classifying triangles by their angles
![]() Uncovering the triangle inequality principle
Uncovering the triangle inequality principle
![]() Poring over the Pythagorean Theorem
Poring over the Pythagorean Theorem
Considering that it’s the runt of the polygon family, the triangle sure does play a big role in geometry. Triangles are one of the most important components of geometry proofs. They also have a great number of interesting properties that you might not expect from the simplest possible polygon. Maybe Leonardo da Vinci (1452–1519) was on to something when he said, “Simplicity is the ultimate sophistication.”
Taking in a Triangle’s Sides
Triangles are classified according to the length of their sides or the measure of their angles. These classifications come in threes, just like the sides and angles themselves.
The following are triangle classifications based on sides:
- Scalene: A triangle with no congruent sides
- Isosceles: A triangle with at least two congruent sides
- Equilateral: A triangle with three congruent sides
Scalene triangles
In addition to having three unequal sides, scalene triangles have three unequal angles. The shortest side is across from the smallest angle, the medium side is across from the medium angle, and the longest side is across from the largest angle.
Isosceles triangles
An isosceles triangle has two (or three) equal sides and two (or three) equal angles. The equal sides are called legs, and the third side is the base. The two angles touching the base (which are congruent) are called base angles. The angle between the two legs is called the vertex angle. See Figure 4-1.

FIGURE 4-1: Two run-of-the-mill isosceles triangles.
Equilateral triangles
An equilateral triangle has three equal sides and three equal angles (which are each ![]() ). Its equal angles make it equiangular as well as equilateral. Note that an equilateral triangle is also isosceles.
). Its equal angles make it equiangular as well as equilateral. Note that an equilateral triangle is also isosceles.
Triangle Classification by Angles
- Acute triangle: A triangle with three acute angles.
- Obtuse triangle: A triangle with one obtuse angle. The other two angles are acute.
- Right triangle: A triangle with a single right angle and two acute angles. The legs of a right triangle are the sides touching the right angle, and the hypotenuse is the side across from the right angle.
The Triangle Inequality Principle

FIGURE 4-2: The triangle inequality principle lets you find the possible lengths of side  .
.
In ![]() , what’s the shortest route from A to B? Naturally, going straight across from A to B is shorter than taking a detour by traveling from A to C and then on to B. That’s the triangle inequality principle in a nutshell.
, what’s the shortest route from A to B? Naturally, going straight across from A to B is shorter than taking a detour by traveling from A to C and then on to B. That’s the triangle inequality principle in a nutshell.
In ![]() , because you know that AB must be less than AC plus CB,
, because you know that AB must be less than AC plus CB, ![]() must be greater than 10; therefore,
must be greater than 10; therefore,
But don’t forget that the same principle applies to the path from A to C; thus, ![]() must be greater than x:
must be greater than x:
You can write both of these answers as a single inequality:
These are the possible lengths of side ![]() . Note that the 2 and the 18 come from the difference and the sum of the other two sides. Figure 4-3 shows this range of lengths. Think of vertex B as a hinge. As the hinge opens more and more, the length of
. Note that the 2 and the 18 come from the difference and the sum of the other two sides. Figure 4-3 shows this range of lengths. Think of vertex B as a hinge. As the hinge opens more and more, the length of ![]() grows.
grows.

FIGURE 4-3: Triangle ABC changes as side  grows.
grows.
Sizing up Triangle Area
I have a feeling you can guess what this section is about.
A triangle’s altitude or height
Imagine that you have a cardboard triangle standing straight up on a table. The altitude of the triangle tells you exactly what you’d expect — the triangle’s height (h) measured from its peak straight down to the table. This height goes down to the base of the triangle that’s flat on the table. Figure 4-4 shows you an example of an altitude.
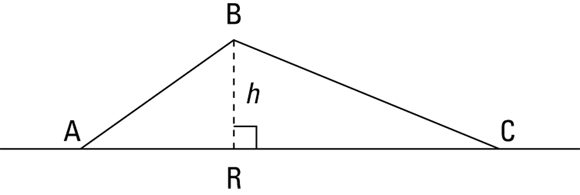
FIGURE 4-4:  is one of the altitudes of
is one of the altitudes of  .
.
Every triangle has three altitudes, one for each side. Figure 4-5 shows the same triangle from Figure 4-4 standing up on a table in the other two possible positions: with ![]() as the base and with
as the base and with ![]() as the base.
as the base.

FIGURE 4-5:  and
and 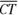 are the other two altitudes of
are the other two altitudes of  .
.
You can use any side of a triangle as a base, regardless of whether that side is on the bottom. Figure 4-6 shows ![]() again with all three of its altitudes.
again with all three of its altitudes.
FIGURE 4-6: Triangle ABC with its three altitudes.
Here’s the lowdown on the location of a triangle’s altitudes:
- Acute triangle: All three altitudes are inside the triangle.
- Right triangle: One altitude is inside the triangle, and the other two altitudes are the legs of the triangle (remember this when figuring the area of a right triangle).
- Obtuse triangle: One altitude is inside the triangle, and two altitudes are outside the triangle.
Determining a triangle’s area
Assume for the sake of argument that you have trouble remembering this formula. Well, you won’t forget it if you focus on why it’s true — which brings me to one of the most important tips in this book.
So why does the area of a triangle equal ![]() ?
?
Because the area of a rectangle is ![]() , and a triangle is half of a rectangle. Check out Figure 4-7, which shows two triangles inscribed in rectangles HALF and PINT.
, and a triangle is half of a rectangle. Check out Figure 4-7, which shows two triangles inscribed in rectangles HALF and PINT.
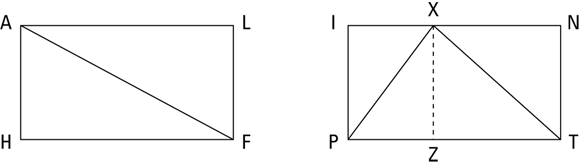
FIGURE 4-7: A triangle takes up half the area of a rectangle.
It should be really obvious that ![]() has half the area of rectangle HALF. And it shouldn’t exactly give you a brain hemorrhage to see that
has half the area of rectangle HALF. And it shouldn’t exactly give you a brain hemorrhage to see that ![]() also has half the area of the rectangle around it. (Triangle PXZ is half of rectangle PIXZ, and
also has half the area of the rectangle around it. (Triangle PXZ is half of rectangle PIXZ, and ![]() is half of rectangle ZXNT.) Because every possible triangle fits in some rectangle just like
is half of rectangle ZXNT.) Because every possible triangle fits in some rectangle just like ![]() fits in rectangle PINT (you just have to put the triangle’s longest side on the bottom), every triangle is half a rectangle.
fits in rectangle PINT (you just have to put the triangle’s longest side on the bottom), every triangle is half a rectangle.
Now for a problem: What’s the length of altitude ![]() in
in ![]() in Figure 4-8?
in Figure 4-8?
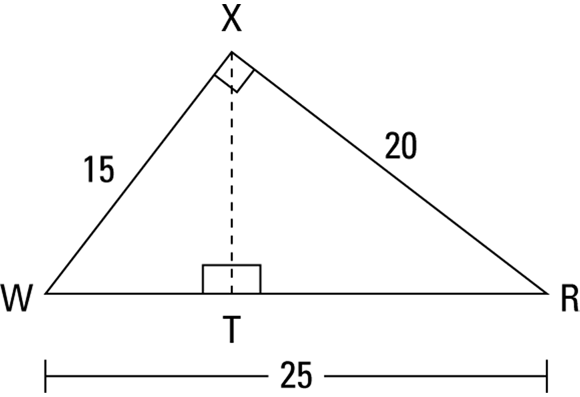
FIGURE 4-8: Right triangle WXR with its three altitudes.
The trick here is to note that because ![]() is a right triangle, legs
is a right triangle, legs ![]() and
and ![]() are also altitudes. So you can use either one as the altitude, and then the other leg automatically becomes the base. Plug their lengths into the formula to determine the triangle’s area:
are also altitudes. So you can use either one as the altitude, and then the other leg automatically becomes the base. Plug their lengths into the formula to determine the triangle’s area:
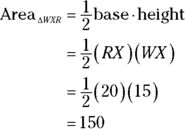
Now you can use the area formula again, using this area of 150, base ![]() , and altitude
, and altitude ![]() :
:

Regarding Right Triangles
In the mathematical universe of all possible triangles, right triangles are extremely rare. But in the real world, right triangles are extremely common. Right angles are everywhere: the corners of almost every wall, floor, ceiling, door, and window; the corners of every book, table, and box; the intersection of most streets; and so on. And everywhere you see a right angle, you potentially have a right triangle. Right triangles abound in navigation, carpentry, and architecture — even the builders of the Great Pyramids in Egypt used right-triangle mathematics. The next section shows you the elegant relationship among the three sides of a right triangle.
The Pythagorean Theorem
Here, a and b are the lengths of the legs and c is the length of the hypotenuse. The legs are the two short sides that touch the right angle, and the hypotenuse (the longest side) is opposite the right angle. Figure 4-9 shows how the Pythagorean Theorem works for a right triangle with legs of 3 and 4 and a hypotenuse of 5.

FIGURE 4-9: The Pythagorean Theorem is as easy as 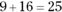 .
.
Here’s a multistage problem in which you have to use the Pythagorean Theorem more than once: In Figure 4-10, find x and the area of hexagon ABCDEF.

FIGURE 4-10: A funny-looking hexagon made up of right triangles.
ABCDEF is made up of four connected right triangles. To get x, you set up a chain reaction in which you solve for the unknown side of one triangle and then use that answer to find the unknown side of the next triangle, and so on. You already know the lengths of two sides of ![]() , so start there to find BF:
, so start there to find BF:
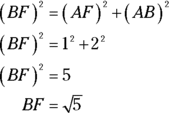
Now that you have BF, you know two of the sides of ![]() . Use the Pythagorean Theorem to find CF:
. Use the Pythagorean Theorem to find CF:

With CF filled in, you can find the short leg of ![]() :
:

And now that you know CE, you can solve for x:

Okay, on to the second half of the problem. To get the area of ABCDEF, just add up the areas of the four right triangles. The area of a triangle is ![]() . For a right triangle, you can use the two legs for the base and the height. Solving for x has already given you the lengths of all the sides of the triangles, so just plug the numbers into the area formula:
. For a right triangle, you can use the two legs for the base and the height. Solving for x has already given you the lengths of all the sides of the triangles, so just plug the numbers into the area formula:

Thus, the area of hexagon ABCDEF is ![]() , or about
, or about ![]() .
.
Pythagorean Triple Triangles
If you use any old numbers for two sides of a right triangle, the Pythagorean Theorem almost always gives you the square root of something for the third side. For example, a right triangle with legs of 5 and 6 has a hypotenuse of ![]() ; if the legs are 3 and 8, the hypotenuse is
; if the legs are 3 and 8, the hypotenuse is ![]() ; and if one of the legs is 6 and the hypotenuse is 9, the other leg works out to
; and if one of the legs is 6 and the hypotenuse is 9, the other leg works out to ![]() , which is
, which is ![]() , or
, or ![]() .
.
A Pythagorean triple triangle is a right triangle with sides whose lengths are all whole numbers, such as 3, 4, and 5 or 5, 12, and 13. People like to use these triangles in problems because they don’t contain those pesky square roots.
The Fab Four triangles
The first four Pythagorean triple triangles are the favorites of geometry problem makers. These triangles, especially the first and second on the list, pop up all over in geometry books.
- The 3-4-5 triangle
- The 5-12-13 triangle
- The 7-24-25 triangle
- The 8-15-17 triangle
Families of Pythagorean triple triangles
Each irreducible Pythagorean triple triangle such as the 5-12-13 triangle is the matriarch of a family with an infinite number of children. The 3 : 4 : 5 family (note the colons), for example, consists of the 3-4-5 triangle and all her offspring. Offspring are created by blowing up or shrinking the 3-4-5 triangle: They include the ![]() triangle, the 6-8-10 triangle, the 21-28-35 triangle (3-4-5 times 7), and their eccentric siblings such as the
triangle, the 6-8-10 triangle, the 21-28-35 triangle (3-4-5 times 7), and their eccentric siblings such as the ![]() triangle and the
triangle and the ![]() triangle. Within any of the triangle families (like the 3 : 4 : 5 family), all the triangles have the same shape.
triangle. Within any of the triangle families (like the 3 : 4 : 5 family), all the triangles have the same shape.
When you know two of the three sides of a right triangle, you can, of course, compute the third side with the Pythagorean Theorem. But if the triangle happens to be a member of one of the Fab Four families, you can use a shortcut. All you need to do is figure out the blow-up or shrink factor that converts the main Fab Four triangle into the given triangle and use that factor to compute the third side of the given triangle.
No-brainer cases
You can often just see that you have one of the Fab Four families and figure out the blow-up or shrink factor in your head. Check out Figure 4-11.

FIGURE 4-11: Two triangles from famous families.
In Figure 4-11a, the digits 8 and 17 in the 0.08 and 0.17 should give you a big hint that this triangle is a member of the 8 : 15 : 17 family. Because 8 divided by 100 is 0.08 and 17 divided by 100 is 0.17, this triangle is an 8-15-17 triangle shrunk down 100 times. Side j is thus 15 divided by 100, or 0.15. This shortcut is way easier than using the Pythagorean Theorem.
Likewise, the digits 3 and 4 should make it a dead giveaway that the triangle in Figure 4-11b is a member of the 3 : 4 : 5 family. Because ![]() is
is ![]() times 3 and
times 3 and ![]() is
is ![]() times 4, you can see that this triangle is a 3-4-5 triangle blown up by a factor of
times 4, you can see that this triangle is a 3-4-5 triangle blown up by a factor of ![]() . Thus, side r is simply
. Thus, side r is simply ![]() times 5, or
times 5, or ![]() .
.
The step-by-step triple triangle method
If you can’t immediately see what Fab Four family a triangle belongs to, you can always use the following step-by-step method to pick the family and find the missing side. Don’t be put off by the length of the method; it’s easier to do than to explain. Check out the triangle in Figure 4-12.
Take the two known sides and make a ratio in fraction form of the smaller to the larger side.
Take the
 and the 6 and make the ratio of
and the 6 and make the ratio of  .
.Reduce this ratio to whole numbers in lowest terms.
If you multiply the top and bottom of
 by 5, you get
by 5, you get  ; that reduces to
; that reduces to  . (With many calculators, this is a snap because they have a function that reduces fractions to lowest terms.)
. (With many calculators, this is a snap because they have a function that reduces fractions to lowest terms.)Look at the fraction from Step 2 to spot the particular triangle family.
The numbers 4 and 5 are part of the 3-4-5 triangle, so you’re dealing with the 3 : 4 : 5 family.
Divide the length of a side from the given triangle by the corresponding number from the family ratio to get your multiplier (which tells you how much the basic triangle has been blown-up or shrunk).
Use the length of the hypotenuse from the given triangle (because working with a whole number is easier) and divide it by the 5 from the 3 : 4 : 5 ratio. You should get
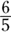 or 1.2 for your multiplier.
or 1.2 for your multiplier.Multiply the third family number (the number you don’t see in the reduced fraction in Step 2) by the result from Step 4 to find the missing side of your triangle.
Three times
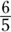 is
is  . That’s the length of side p; and that’s a wrap.
. That’s the length of side p; and that’s a wrap.
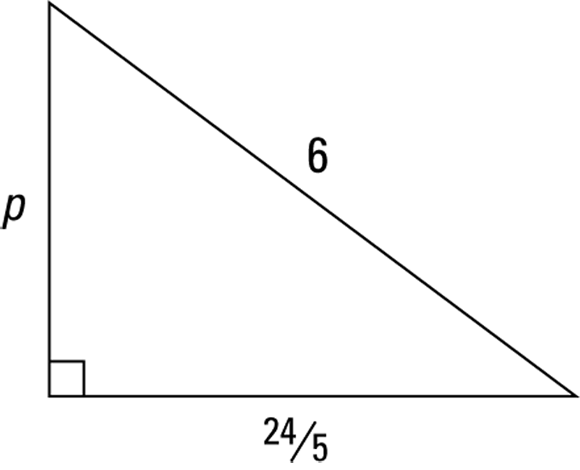
FIGURE 4-12: Use a ratio to figure out what family this triangle belongs to.
You may be wondering why you should go through all this trouble when you could just use the Pythagorean Theorem. Good point. The Pythagorean Theorem is easier for some triangles (especially if you’re allowed to use your calculator). But — take my word for it — this triple triangle technique can come in handy. Take your pick.
Two Special Right Triangles
Make sure you know the two right triangles in this section: the ![]() triangle and the
triangle and the ![]() triangle. They come up in many, many geometry problems, not to mention their frequent appearance in trigonometry, precalculus, and calculus. Despite the pesky irrational (square-root) lengths they have for some of their sides, they’re both more basic and more important than the Pythagorean triple triangles in the previous section. They’re more basic because they’re the progeny of the square and equilateral triangle, and they’re more important because their angles are nice fractions of a right angle.
triangle. They come up in many, many geometry problems, not to mention their frequent appearance in trigonometry, precalculus, and calculus. Despite the pesky irrational (square-root) lengths they have for some of their sides, they’re both more basic and more important than the Pythagorean triple triangles in the previous section. They’re more basic because they’re the progeny of the square and equilateral triangle, and they’re more important because their angles are nice fractions of a right angle.
The 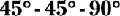 triangle
triangle
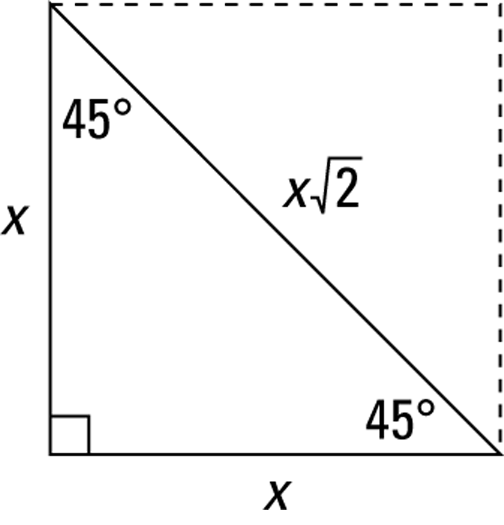
FIGURE 4-13: The  triangle.
triangle.
Try a couple of problems. Find the lengths of the unknown sides in triangles BAT and BOY shown in Figure 4-14.
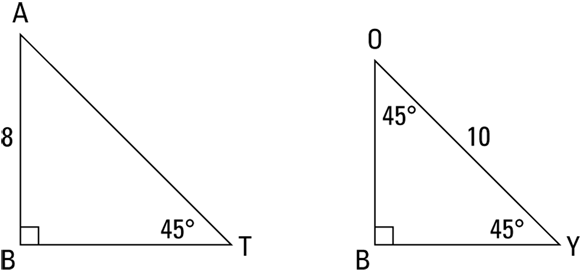
FIGURE 4-14: Find the missing lengths.
You can solve ![]() triangle problems in two ways: the formal book method and the street-smart method. Try ’em both and take your pick. The formal method uses the ratio of the sides from Figure 4-13.
triangle problems in two ways: the formal book method and the street-smart method. Try ’em both and take your pick. The formal method uses the ratio of the sides from Figure 4-13.
For ![]() , because one of the legs is 8, the x in the ratio is 8. Plugging 8 into the three x’s gives you
, because one of the legs is 8, the x in the ratio is 8. Plugging 8 into the three x’s gives you
And for ![]() , the hypotenuse is 10, so you set the
, the hypotenuse is 10, so you set the ![]() from the ratio equal to 10 and solve for x:
from the ratio equal to 10 and solve for x:

That does it:
- If you know a leg and want to compute the hypotenuse (a longer thing), you multiply by
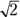 . In Figure 4-14, one of the legs in
. In Figure 4-14, one of the legs in 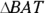 is 8, so you multiply that by
is 8, so you multiply that by  to get the longer hypotenuse —
to get the longer hypotenuse —  .
. - If you know the hypotenuse and want to compute the length of a leg (a shorter thing), you divide by
 . In Figure 4-14, the hypotenuse in
. In Figure 4-14, the hypotenuse in 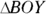 is 10, so you divide that by
is 10, so you divide that by 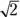 to get the shorter legs; they’re each
to get the shorter legs; they’re each  or
or  .
.

FIGURE 4-15: The 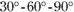 triangle.
triangle.
The  triangle
triangle
Here are a couple of problems. Find the lengths of the unknown sides in ![]() and
and ![]() in Figure 4-16.
in Figure 4-16.
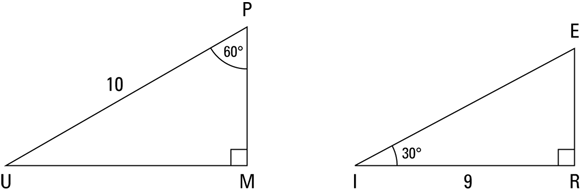
FIGURE 4-16: Find the missing lengths.
You can solve ![]() triangles with the textbook method or the street-smart method. The textbook method begins with the ratio of the sides from Figure 4-15:
triangles with the textbook method or the street-smart method. The textbook method begins with the ratio of the sides from Figure 4-15:
In ![]() , the hypotenuse is 10, so you set 2x equal to 10 and solve for x, getting
, the hypotenuse is 10, so you set 2x equal to 10 and solve for x, getting ![]() . Now just plug 5 in for the x’s, and you have
. Now just plug 5 in for the x’s, and you have ![]() :
:
In ![]() , the long leg is 9, so set
, the long leg is 9, so set ![]() equal to 9 and solve:
equal to 9 and solve:
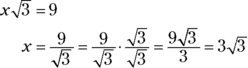
Plug in the value of x, and you’re done:

- The relationship between the short leg and the hypotenuse is a no-brainer: The hypotenuse is twice as long as the short leg. So if you know one of them, you can get the other in your head. The
 method mainly concerns the connection between the short and long legs.
method mainly concerns the connection between the short and long legs. - If you know the short leg and want to compute the long leg (a longer thing), you multiply by
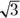 . If you know the long leg and want to compute the short leg (a shorter thing), you divide by
. If you know the long leg and want to compute the short leg (a shorter thing), you divide by  .
.
Try the street-smart method with the triangles in Figure 4-16. The hypotenuse in ![]() is 10, so first you cut that in half to get the length of the short leg, which is thus 5. Then to get the longer leg, you multiply that by
is 10, so first you cut that in half to get the length of the short leg, which is thus 5. Then to get the longer leg, you multiply that by ![]() , which gives you
, which gives you ![]() . In
. In ![]() , the long leg is 9, so to get the shorter leg, you divide that by
, the long leg is 9, so to get the shorter leg, you divide that by ![]() , which gives you
, which gives you ![]() , or
, or ![]() . The hypotenuse is twice that,
. The hypotenuse is twice that, ![]() .
.
With the ![]() triangle (and also with the
triangle (and also with the ![]() triangle), there will almost always be one or two sides whose lengths contain a square root symbol (in unusual cases, all three sides could contain a radical symbol). But it’s impossible to have no square roots — which brings me to the following warning.
triangle), there will almost always be one or two sides whose lengths contain a square root symbol (in unusual cases, all three sides could contain a radical symbol). But it’s impossible to have no square roots — which brings me to the following warning.

 The triangle inequality principle: The sum of the lengths of any two sides of a triangle must be greater than the length of the third side. This principle comes up in a fair number of problems, so don’t forget it! It’s based on the simple fact that the shortest distance between two points is a straight line. Check out
The triangle inequality principle: The sum of the lengths of any two sides of a triangle must be greater than the length of the third side. This principle comes up in a fair number of problems, so don’t forget it! It’s based on the simple fact that the shortest distance between two points is a straight line. Check out  Whenever possible, don’t just memorize math concepts, formulas, and so on by rote. Try to understand why they’re true. When you grasp the whys underlying the ideas, you remember them better and develop a deeper appreciation of the interconnections among mathematical ideas. That appreciation makes you a more successful math student.
Whenever possible, don’t just memorize math concepts, formulas, and so on by rote. Try to understand why they’re true. When you grasp the whys underlying the ideas, you remember them better and develop a deeper appreciation of the interconnections among mathematical ideas. That appreciation makes you a more successful math student. Make sure the sides of the given triangle match up correctly with the sides of the Fab Four triangle family you’re using. In a 3 : 4 : 5 triangle, for example, the legs must be the 3 and the 4, and the hypotenuse must be the 5. So a triangle with legs of 30 and 50 (despite the 3 and the 5) is not in the 3 : 4 : 5 family because the 50 (the 5) is one of the legs instead of the hypotenuse.
Make sure the sides of the given triangle match up correctly with the sides of the Fab Four triangle family you’re using. In a 3 : 4 : 5 triangle, for example, the legs must be the 3 and the 4, and the hypotenuse must be the 5. So a triangle with legs of 30 and 50 (despite the 3 and the 5) is not in the 3 : 4 : 5 family because the 50 (the 5) is one of the legs instead of the hypotenuse.