Chapter 3
Tackling a Longer Proof
IN THIS CHAPTER
![]() Making a game plan
Making a game plan
![]() Starting at the start, working from the end, and meeting in the middle
Starting at the start, working from the end, and meeting in the middle
![]() Making sure your logic holds
Making sure your logic holds
Chapter 2 started you off with short proofs and a dozen and a half basic theorems. Here, I go through a single, longer proof in great detail, carefully analyzing each step. Throughout the chapter, I walk you through the entire thought process that goes into solving a proof, reviewing and expanding on the half dozen or so proof strategies from Chapter 2. When you’re working on a proof and you get stuck, this chapter is a good one to come back to for tips on how to get moving again. The proof I’ve created for this chapter isn’t so terribly gnarly; it’s just a bit longer than the ones in Chapter 2. Here it is:


Making a Game Plan
A good way to begin any proof is to make a game plan, or rough outline, of how you’d do the proof. A game plan is your common sense argument of how you’d get from the given facts to the thing you’re trying to prove. The nice thing about a game plan is that you don’t need to worry about what theorems you’ll need to use or how you’ll write out the formal proof.
Here’s one possible game plan for the proof we’re working on: The givens provide you with two pairs of perpendicular segments; that gives you ![]() for
for ![]() and
and ![]() . Then, say congruent angles
. Then, say congruent angles![]() and
and ![]() are both
are both ![]() . That would make
. That would make ![]() and
and ![]() both equal to
both equal to ![]() . Next, because
. Next, because ![]() and
and ![]() are complementary, as are
are complementary, as are ![]() and
and ![]() ,
, ![]() and
and ![]() would both be
would both be ![]() . Angles 5 and 8 are congruent vertical angles, as are
. Angles 5 and 8 are congruent vertical angles, as are ![]() and
and ![]() , so
, so ![]() and
and ![]() would also have to be
would also have to be ![]() — and thus they’re congruent. Finally, because
— and thus they’re congruent. Finally, because ![]() ,
, ![]() is bisected. That does it.
is bisected. That does it.
Using All the Givens
Perhaps you don’t follow the game plan in the previous section — or you get it but don’t think you would’ve been able to come up with it on your own in one shot — and so you’re staring at the proof and just don’t know where to begin. My advice: Check all the givens in the proof and ask yourself why they’d tell you each given.

FIGURE 3-1: The first two lines of the proof.
Using If-Then Logic
Moving from the givens to the final conclusion in a two-column proof is like knocking over a row of dominoes: Just as each domino knocks over the next domino, each proof statement leads to the next statement. The if-then sentence structure of each reason in a two-column proof shows you how each statement “knocks over” the next statement. In Figure 3-1, for example, you see the reason “if two segments are perpendicular, then they form a right angle.” The perpendicular domino (statement 1) knocks over the right-angle domino (statement 2). This process continues throughout the whole proof.
- The idea or ideas in the if clause of a reason must appear in the statement column somewhere above the line of that reason.
- The single idea in the then clause of a reason must be the same idea that’s in the statement directly across from the reason.
Look back at Figure 3-1. Because statement 1 is the only statement above reason 2, it’s the only place you can look for the ideas that go in the if clause of reason 2. So if you begin this proof by putting the two pairs of perpendicular segments in statement 1, then you have to use that information in reason 2, which must therefore begin “if segments are perpendicular, then …”
Now say you didn’t know what to put in statement 2. The if-then structure of reason 2 helps you out. Because reason 2 begins “if two segments are perpendicular …” you’d ask yourself, “Well, what happens when two segments are perpendicular?” The answer, of course, is that right angles are formed. The right-angle idea must therefore go in the then clause of reason 2 and right across from it in statement 2.
Okay, now what? Well, think about reason 3. One way it could begin is with the right angles from statement 2. The if clause of reason 3 might be “if two angles are right angles …” Can you finish that? Of course: If two angles are right angles, then they’re congruent. So that’s it: You’ve got reason 3, and statement 3 must contain the idea from the then clause of reason 3, the congruence of right angles. Figure 3-2 shows you the proof so far.

FIGURE 3-2: The first three lines of the proof.
Chipping Away at the Problem
Face it: You’re going to get stuck at one point or another while working on proofs. Here’s a tip for getting unstuck.
So far in the proof in this chapter, you have the two congruent angles in statement 3, but you can’t make more progress with that idea alone. So check out the givens again. Which of the three unused givens might build on statement 3? There’s no way to know for sure, so you need to trust your instincts, pick a given, and try it.
The third given says ![]() . That looks promising because angles 1 and 2 are part of the right angles from statement 3. You should ask yourself, “What would follow if
. That looks promising because angles 1 and 2 are part of the right angles from statement 3. You should ask yourself, “What would follow if ![]() and
and ![]() were, say,
were, say, ![]() ?” You know the right angles are
?” You know the right angles are ![]() , so if
, so if ![]() and
and ![]() were
were ![]() , then
, then ![]() and
and ![]() would both have to be
would both have to be ![]() and thus, obviously, they’d be congruent. That’s it. You’re making progress. You can use that third given in statement 4 and then state that
and thus, obviously, they’d be congruent. That’s it. You’re making progress. You can use that third given in statement 4 and then state that ![]() in statement 5.
in statement 5.
Figure 3-3 shows the proof up to statement 5. The bubbles and arrows show you how the statements and reasons connect to each other. You can see that the if clause of each reason connects to a statement from above the reason and that the then clause connects to the statement on the same line as the reason. Because I haven’t gone over reason 5 yet, it’s not in the figure. See whether you can figure out reason 5 before reading the explanation that follows.

FIGURE 3-3: The first five lines of the proof (minus reason 5).
So, did you figure out reason 5? It’s angle subtraction because ![]() and
and ![]() in statement 5 ended up being
in statement 5 ended up being ![]() angles (assuming
angles (assuming ![]() and
and ![]() were
were ![]() ), and you get the answer of
), and you get the answer of ![]() by doing a subtraction problem,
by doing a subtraction problem, ![]() . You’re subtracting two angles from two other angles, so you use the four-angle version of angle subtraction (see Chapter 2). Reason 5 is, therefore, “If two congruent angles (
. You’re subtracting two angles from two other angles, so you use the four-angle version of angle subtraction (see Chapter 2). Reason 5 is, therefore, “If two congruent angles (![]() and
and ![]() ) are subtracted from two other congruent angles (the right angles), then the differences (
) are subtracted from two other congruent angles (the right angles), then the differences (![]() and
and ![]() ) are congruent.”
) are congruent.”
At this stage, you may feel a bit disconcerted if you don’t know where these five lines are taking you or whether they’re correct or not. Here’s a tip.
Working Backward
Assume that you’re in the middle of a proof and you can’t see how to get to the finish line from where you are now. No worries — just jump to the end of the proof and work backward.
Okay, so picking up where I left off on this chapter’s proof: You’ve completed five lines of the proof, and you’re up to ![]() . Where to now? Going forward from here might be a bit tricky, so work backward. You know that the final line of the proof has to be the prove statement:
. Where to now? Going forward from here might be a bit tricky, so work backward. You know that the final line of the proof has to be the prove statement: ![]() bisects
bisects ![]() . Now, if you think about what the final reason has to be or what the second-to-last statement should be, it shouldn’t be too hard to see that you need to have two congruent angles to conclude that a larger angle is bisected. Figure 3-4 shows you what the end of the proof looks like.
. Now, if you think about what the final reason has to be or what the second-to-last statement should be, it shouldn’t be too hard to see that you need to have two congruent angles to conclude that a larger angle is bisected. Figure 3-4 shows you what the end of the proof looks like.
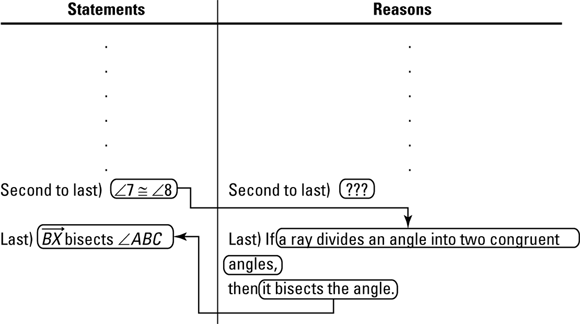
FIGURE 3-4: The proof’s last two lines.
Try to continue going backward to the third-to-last statement, the fourth-to-last statement, and so on. (Working backward through a proof always involves some guesswork, but don’t let that stop you.) Why might ![]() be congruent to
be congruent to ![]() ? Well, you probably don’t have to look too hard to spot the pair of congruent vertical angles
? Well, you probably don’t have to look too hard to spot the pair of congruent vertical angles ![]() and
and ![]() and the other pair,
and the other pair, ![]() and
and ![]() . Okay, so you want to show that
. Okay, so you want to show that ![]() is congruent to
is congruent to ![]() , and you know that
, and you know that ![]() equals
equals ![]() and
and ![]() equals
equals ![]() . So if you were to know that
. So if you were to know that ![]() and
and ![]() are congruent, you’d be home free.
are congruent, you’d be home free.
Now that you’ve worked backward a number of steps, here’s the argument in the forward direction: The proof could end by stating in the fourth-to-last statement that ![]() , then in the third-to-last that
, then in the third-to-last that ![]() and
and ![]() (because vertical angles are congruent), and then in the second-to-last that
(because vertical angles are congruent), and then in the second-to-last that ![]() by the Transitive Property (for four angles). Figure 3-5 shows how this all looks written out in the two-column format.
by the Transitive Property (for four angles). Figure 3-5 shows how this all looks written out in the two-column format.
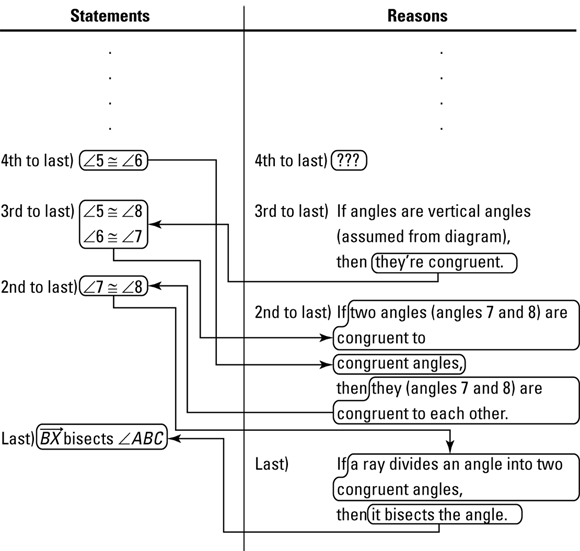
FIGURE 3-5: The end of the proof (so far).
Filling in the Gaps
Working backward from the end of a proof is a great strategy. You can’t always work as far backward as I did in this proof — sometimes you can only get to the second-to-last statement or maybe to the third-to-last. But even if you fill in only one or two statements (in addition to the automatic final statement), those additions can be very helpful. After making the additions, the proof is easier to finish because your new “final” destination (say the third-to-last statement) is fewer steps away from the beginning of the proof and is thus an easier goal to aim for.
Okay, let’s wrap up this proof. All that remains is to bridge the gap between statement ![]() and the fourth-to-last statement
and the fourth-to-last statement ![]() . There are two givens you haven’t used yet, so they must be the key to finishing the proof.
. There are two givens you haven’t used yet, so they must be the key to finishing the proof.
How can you use the givens about the two pairs of complementary angles? Try the plugging-in-numbers idea again. Use the same numbers you used before, and say that congruent angles ![]() and
and ![]() are each
are each ![]() . Angle 5 is complementary to
. Angle 5 is complementary to ![]() , so
, so ![]() would have to be
would have to be ![]() . Angle 6 is complementary to
. Angle 6 is complementary to ![]() , so
, so ![]() also ends up being
also ends up being ![]() . That does it —
. That does it — ![]() and
and ![]() are congruent, and you’ve connected the loose ends. All that’s left is to finish writing out the formal proof.
are congruent, and you’ve connected the loose ends. All that’s left is to finish writing out the formal proof.
Writing out the Finished Proof
Sound the trumpets! Here’s the finished proof complete with the flow-of-logic bubbles (see Figure 3-6). (This time, I’ve put in only the arrows that connect to the if clause of each reason. You know that each reason’s then clause must connect to the statement on the same line.) If you understand all the strategies and tips covered in this chapter and you can follow every step of this proof, you should be able to handle any proof they throw at you.

FIGURE 3-6: The finished proof.

 When you’re working through a game plan, it’s sometimes a good idea to make up arbitrary numbers for the segments and angles in the givens and for unmentioned segments and angles. You should not, however, make up numbers for segments and angles that you’re trying to show are congruent. This optional step makes the proof diagram more concrete and makes it easier for you to get a handle on how the proof works.
When you’re working through a game plan, it’s sometimes a good idea to make up arbitrary numbers for the segments and angles in the givens and for unmentioned segments and angles. You should not, however, make up numbers for segments and angles that you’re trying to show are congruent. This optional step makes the proof diagram more concrete and makes it easier for you to get a handle on how the proof works. Make sure that the if-then structure of your reasons is correct.
Make sure that the if-then structure of your reasons is correct.