Chapter 5
Congruent Triangle Proofs
IN THIS CHAPTER
![]() Proving triangles congruent with SSS, SAS, ASA, AAS, and HLR
Proving triangles congruent with SSS, SAS, ASA, AAS, and HLR
![]() CPCTC: Focusing on parts of congruent triangles
CPCTC: Focusing on parts of congruent triangles
![]() Eying the two isosceles triangle theorems
Eying the two isosceles triangle theorems
![]() Working with the equidistance theorems
Working with the equidistance theorems
You’ve arrived at high school geometry’s main event: triangle proofs. The proofs in Chapters 2 and 3 are complete proofs that show you how proofs work, and they illustrate many of the most important proof strategies. But they’re sort of just warm-up or preliminary proofs that lay the groundwork for the real, full-fledged triangle proofs you see in this chapter.
Proving Triangles Congruent
Before learning how to prove that triangles are congruent, you’ve got to know what congruent triangles are, right? Here you go … .
Maybe the best way to think about what it means for two triangles (or any other shapes) to be congruent is that you could move them around (by shifting, rotating, and/or flipping them) so that they’d stack perfectly on top of one another. You indicate that triangles are congruent with a statement such as ![]() , which means that vertex A (the first letter) corresponds with and would stack on vertex X (the first letter), B would stack on Y, and C would stack on Z. Side
, which means that vertex A (the first letter) corresponds with and would stack on vertex X (the first letter), B would stack on Y, and C would stack on Z. Side ![]() would stack on side
would stack on side ![]() ,
, ![]() would stack on
would stack on ![]() , and so on.
, and so on.
So now, on to the methods for proving triangles congruent. There are five ways: SSS, SAS, ASA, AAS, and HLR.
SSS: The side-side-side method

FIGURE 5-1: Triangles with congruent sides are congruent.
You can use SSS in the following “TRIANGLE” proof:
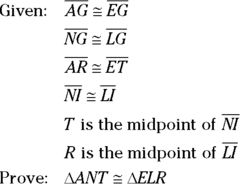

First, come up with a game plan. Here’s how that might work.
You know you’ve got to prove the triangles congruent, so your first question should be “Can you show that the three pairs of corresponding sides are congruent?” Sure, you can do that:
- Subtract
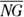 and
and 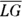 from
from 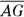 and
and  to get the first pair of congruent sides,
to get the first pair of congruent sides,  and
and 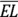 .
. - Subtract
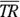 from
from  and
and 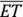 to get the second pair of congruent sides,
to get the second pair of congruent sides, 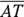 and
and 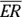 .
. - Cut congruent segments
 and
and  in half to get the third pair,
in half to get the third pair,  and
and  . That’s it.
. That’s it.
To make the game plan more tangible, you may want to make up lengths for the various segments. For instance, say ![]() and
and ![]() are 9,
are 9, ![]() and
and ![]() are 3,
are 3, ![]() and
and ![]() are 8,
are 8, ![]() is 3, and
is 3, and ![]() and
and ![]() are 8. When you do the math, you see that
are 8. When you do the math, you see that ![]() and
and ![]() both end up with sides of 4, 5, and 6, which means, of course, that they’re congruent.
both end up with sides of 4, 5, and 6, which means, of course, that they’re congruent.
Here’s how the formal proof shapes up:

Note: After SSS in the final step, I indicate the three lines from the statement column where I’ve shown the three pairs of sides to be congruent. You don’t have to do this, but it’s a good idea. It can help you avoid some careless mistakes. Remember that each of the three lines you list must show a congruence of segments (or angles, if you’re using one of the other approaches to proving triangles congruent).
SAS: Side-angle-side
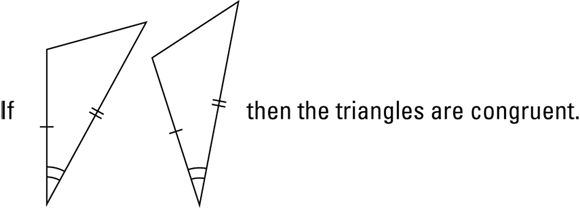
FIGURE 5-2: Two sides and the angle between them make these triangles congruent.
Check out the SAS postulate in action:

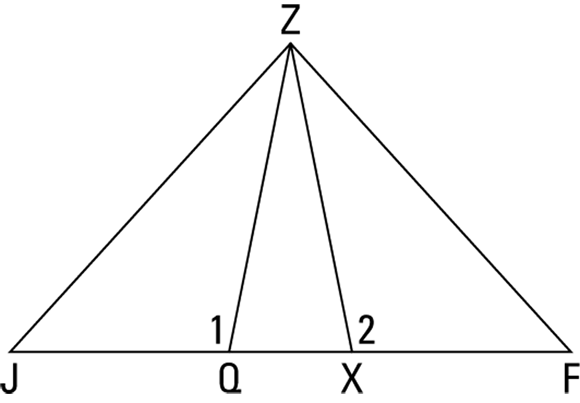
Figure 5-3 shows you what this proof diagram looks like with the triangles separated.
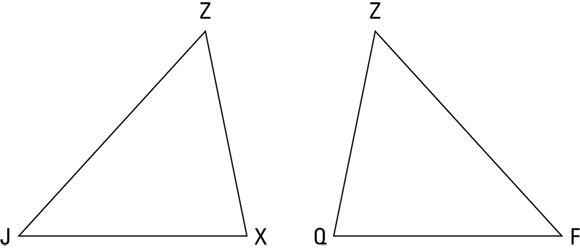
FIGURE 5-3: An amicable separation of triangles.
Looking at Figure 5-3, you can easily see that the triangles are congruent (they’re mirror images of each other). You also see that, for example, side ![]() corresponds to side
corresponds to side ![]() and that
and that ![]() corresponds to
corresponds to ![]() .
.
So using both diagrams, here’s a possible game plan:
- Determine which congruent triangle postulate is likely to be the ticket for proving the triangles congruent. You know you have to prove the triangles congruent, and one of the givens is about angles, so SAS looks like a better candidate than SSS for the final reason. (You don’t have to figure this out now, but it’s not a bad idea to at least have a guess about the final reason.)
- Look at the givens and think about what they tell you about the triangles. Triangle QZX is isosceles, so that tells you
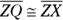 . Look at these sides in both figures. Put tick marks on
. Look at these sides in both figures. Put tick marks on  and
and 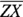 in Figure 5-3 to show that you know they’re congruent. Now consider why they’d tell you the next given,
in Figure 5-3 to show that you know they’re congruent. Now consider why they’d tell you the next given,  . Well, what if they were both 6 and
. Well, what if they were both 6 and 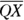 were 2?
were 2? 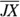 and
and 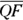 would both be 8, so you have a second pair of congruent sides. Put tick marks on Figure 5-3 to show this congruence.
would both be 8, so you have a second pair of congruent sides. Put tick marks on Figure 5-3 to show this congruence. - Find the pair of congruent angles. Look at Figure 5-3 again. If you can show that
 is congruent to
is congruent to  , you’ll have SAS. Do you see where
, you’ll have SAS. Do you see where 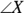 and
and  fit into the original diagram? Note that they’re the supplements of
fit into the original diagram? Note that they’re the supplements of 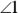 and
and  . That does it. Angles 1 and 2 are congruent, so their supplements are congruent as well. (If you fill in numbers, you can see that if
. That does it. Angles 1 and 2 are congruent, so their supplements are congruent as well. (If you fill in numbers, you can see that if 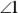 and
and 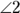 are both
are both 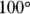 ,
,  and
and  would both be
would both be  .)
.)
Here’s the formal proof:

ASA: The angle-side-angle tack
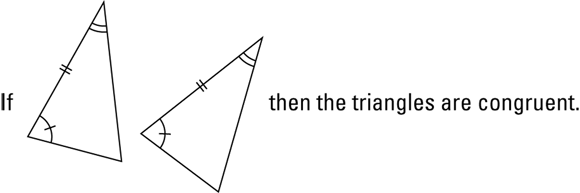
FIGURE 5-4: Two angles and their shared side make these triangles congruent.
AAS: Angle-angle-side

FIGURE 5-5: Two congruent angles and a side not between them make these triangles congruent.
Like ASA, to use AAS, you need two pairs of congruent angles and one pair of congruent sides to prove two triangles congruent. But for AAS, the two angles and one side in each triangle must go in the order angle-angle-side (going around the triangle either clockwise or counterclockwise).
Last but not least: HLR
In other books, HLR is usually called HL. Rebel that I am, I’m boldly renaming it HLR because its three letters emphasize that — as with SSS, SAS, ASA, and AAS — before you can use it in a proof, you need to have three things in the statement column (congruent hypotenuses, congruent legs, and right angles).
Taking the Next Step with CPCTC
In the preceding section, the relatively short proofs end with showing that two triangles are congruent. But in more advanced proofs, showing triangles congruent is just a stepping stone for going on to prove other things. In this section, you take proofs a step further.
Defining CPCTC
Because congruent triangles have six pairs of congruent parts (three pairs of segments and three pairs of angles) and you need three of the pairs for SSS, SAS, ASA, AAS, or HLR, there will always be three remaining pairs that you didn’t use. The purpose of CPCTC is to show one or more of these remaining pairs congruent.
CPCTC is very easy to use. After you show that two triangles are congruent, you can state that two of their sides or angles are congruent on the next line of the proof, using CPCTC as the justification for that statement. This group of two consecutive lines makes up the core or heart of many proofs.
Say you’re in the middle of some proof (shown in Figure 5-6), and by line 6, you’re able to show with ASA that ![]() is congruent to
is congruent to ![]() . The tick marks in the diagram show the pair of congruent sides and the two pairs of congruent angles that were used for ASA. Now that you know that the triangles are congruent, you can state on line 7 that
. The tick marks in the diagram show the pair of congruent sides and the two pairs of congruent angles that were used for ASA. Now that you know that the triangles are congruent, you can state on line 7 that ![]() and use CPCTC for the reason. (You could also use CPCTC to justify that
and use CPCTC for the reason. (You could also use CPCTC to justify that ![]() or that
or that ![]() .)
.)

FIGURE 5-6: A critical pair of proof lines: Congruent triangles and CPCTC.
Tackling a CPCTC proof
Check out CPCTC in action in the next proof. But before I get there, here’s a property you need to do the problem. It’s an incredibly simple concept that comes up in many proofs.
Whenever you see two triangles that share a side or an angle, that side or angle belongs to both triangles. With the Reflexive Property, the shared side or angle becomes a pair of congruent sides or angles that you can use as one of the three pairs of congruent things that you need to prove the triangles congruent.
Here’s your CPCTC proof:


Before you write out the formal proof, come up with a game plan. Here’s one possibility:
- Look for congruent triangles. The congruent triangles should just about jump out at you from this diagram. Think about how you’ll show that they’re congruent. The triangles share side
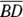 , giving you one pair of congruent sides.
, giving you one pair of congruent sides.  is an altitude, so that gives you congruent right angles. And because
is an altitude, so that gives you congruent right angles. And because  is a median,
is a median,  . That does it; you have SAS. (Note that even though you’ve got right triangles here, you do not use HLR. That wouldn’t work because you don’t know anything about the hypotenuses.)
. That does it; you have SAS. (Note that even though you’ve got right triangles here, you do not use HLR. That wouldn’t work because you don’t know anything about the hypotenuses.) - Now think about what you have to prove and what you’d need to know to get there. To conclude that
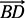 bisects
bisects  , you need
, you need  in the second-to-last line. And how will you get that? Why, with CPCTC, of course!
in the second-to-last line. And how will you get that? Why, with CPCTC, of course!
Here’s the two-column proof:

The Isosceles Triangle Theorems
The earlier sections in this chapter involve pairs of congruent triangles. Here, you get two theorems that involve a single isosceles triangle. Although you often need these theorems for proofs in which you show that two triangles are congruent, the theorems themselves concern only one triangle.
- If sides, then angles: If two sides of a triangle are congruent, then the angles opposite those sides are congruent (see Figure 5-7).
- If angles, then sides: If two angles of a triangle are congruent, then the sides opposite those angles are congruent (see Figure 5-8).
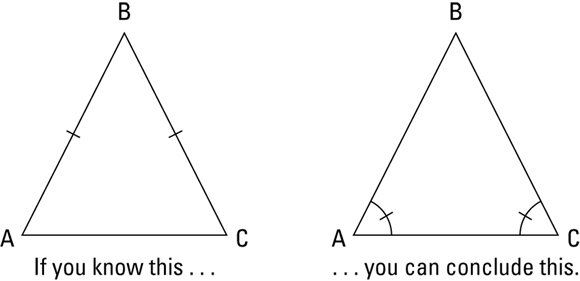
FIGURE 5-7: The congruent sides tell you that the angles are congruent.
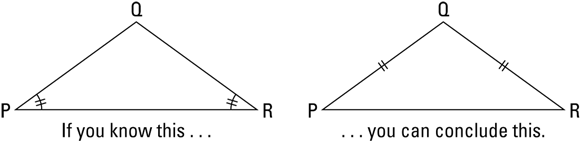
FIGURE 5-8: The congruent angles tell you that the sides are congruent.
Here’s a proof. Try to work through a game plan and/or a formal proof on your own before reading the ones below.


Here’s a game plan:
- Check the proof diagram for isosceles triangles and pairs of congruent triangles. This proof’s diagram has an isosceles triangle, which is a huge hint that you’ll likely use one of the isosceles triangle theorems. You also have a pair of triangles that look congruent (the overlapping ones), which is another huge hint that you’ll want to show that they’re congruent.
- Think about how to finish the proof with a triangle congruence theorem and CPCTC. You’re given the sides of the isosceles triangle, so that gives you congruent angles. You’re also given
 , so that gives you a second pair of congruent angles. If you can get
, so that gives you a second pair of congruent angles. If you can get 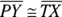 , you’d have ASA. And you can get that by adding
, you’d have ASA. And you can get that by adding  to the given congruent segments,
to the given congruent segments,  and
and  . You finish with CPCTC.
. You finish with CPCTC.

The Two Equidistance Theorems
Although congruent triangles are the focus of this chapter, in this section, I give you two theorems that you can often use instead of proving triangles congruent. Even though you see congruent triangles in this section’s proof diagrams, you don’t have to prove the triangles congruent; one of the equidistance theorems gives you a shortcut to the prove statement.
Determining a perpendicular bisector
The first equidistance theorem tells you that two points determine the perpendicular bisector of a segment. (To “determine” something means to lock in its position, basically to show you where something is.)
The best way to understand this royal mouthful is visually. Consider the kite-shaped diagram in Figure 5-9.
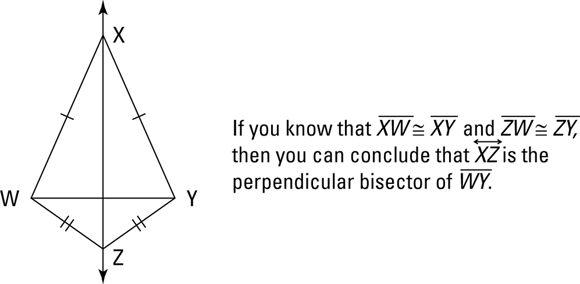
FIGURE 5-9: The first equidistance theorem.
The theorem works like this: If you have one point (like X) that’s equally distant from the endpoints of a segment (W and Y) and another point (like Z) that’s also equally distant from the endpoints, then the two points (X and Z) determine the perpendicular bisector of that segment ![]() . You can also see the meaning of the short form of the theorem in this diagram: If you have two pairs of congruent segments (
. You can also see the meaning of the short form of the theorem in this diagram: If you have two pairs of congruent segments (![]() and
and ![]() ), then there’s a perpendicular bisector (
), then there’s a perpendicular bisector (![]() is the perpendicular bisector of
is the perpendicular bisector of ![]() ).
).
Here’s a “SHORT” proof that shows how to use the first equidistance theorem as a shortcut that allows you to do the proof without having to show that the triangles are congruent.
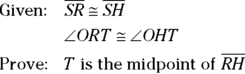

You can do this proof using congruent triangles, but it’d take you about nine steps and you’d have to use two different pairs of congruent triangles.

Using a perpendicular bisector
With the second equidistance theorem, you use a point on a perpendicular bisector to prove two segments congruent.

FIGURE 5-10: The second equidistance theorem.
This theorem tells you that if you begin with a segment (like ![]() ) and its perpendicular bisector (like
) and its perpendicular bisector (like ![]() ) and you have a point on the perpendicular bisector (like N), then that point is equally distant from the endpoints of the segment.
) and you have a point on the perpendicular bisector (like N), then that point is equally distant from the endpoints of the segment.

 Congruent triangles: Triangles in which all pairs of corresponding sides and angles are congruent.
Congruent triangles: Triangles in which all pairs of corresponding sides and angles are congruent. SSS (Side-Side-Side): If the three sides of one triangle are congruent to the three sides of another triangle, then the triangles are congruent.
SSS (Side-Side-Side): If the three sides of one triangle are congruent to the three sides of another triangle, then the triangles are congruent.  When overlapping triangles muddy your understanding of a proof diagram, try redrawing the diagram with the triangles separated. Doing so can give you a clearer idea of how the triangles’ sides and angles relate to each other. Focusing on your new diagram may make it easier to figure out what you need to prove the triangles congruent. However, you still need to use the original diagram to understand some parts of the proof, so use the second diagram as a sort of aid to get a better handle on the original diagram.
When overlapping triangles muddy your understanding of a proof diagram, try redrawing the diagram with the triangles separated. Doing so can give you a clearer idea of how the triangles’ sides and angles relate to each other. Focusing on your new diagram may make it easier to figure out what you need to prove the triangles congruent. However, you still need to use the original diagram to understand some parts of the proof, so use the second diagram as a sort of aid to get a better handle on the original diagram. ASS and SSA don’t prove anything, so don’t try using ASS (or its backward twin, SSA) to prove triangles congruent. You can use SSS, SAS, ASA, and AAS (or SAA, the backward twin of AAS) to prove triangles congruent, but not ASS. In short, every three-letter combination of A’s and S’s proves something unless it spells ass or is ass backward. (You work with AAA in
ASS and SSA don’t prove anything, so don’t try using ASS (or its backward twin, SSA) to prove triangles congruent. You can use SSS, SAS, ASA, and AAS (or SAA, the backward twin of AAS) to prove triangles congruent, but not ASS. In short, every three-letter combination of A’s and S’s proves something unless it spells ass or is ass backward. (You work with AAA in