Chapter 8
Similarity
IN THIS CHAPTER
![]() Sizing up similar figures
Sizing up similar figures
![]() Doing similar triangle proofs
Doing similar triangle proofs
![]() Scoping out theorems about proportionality
Scoping out theorems about proportionality
You know the meaning of the word similar in everyday speech. In geometry, it has a related but more technical meaning. Two figures are similar if they have exactly the same shape.
Similar Figures
In this section, I cover the formal definition of similarity, how similar figures are named, and how they’re positioned.
Defining similar polygons
As you see in Figure 8-1, quadrilateral WXYZ is the same shape as quadrilateral ABCD, but it’s ten times larger (though not drawn to scale). These quadrilaterals are therefore similar.
- Corresponding angles are congruent.
- Corresponding sides are proportional.
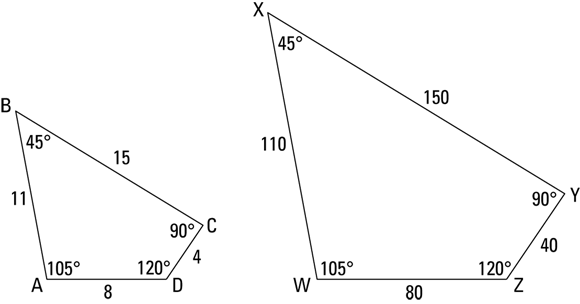
FIGURE 8-1: These quadrilaterals are similar because they’re exactly the same shape; note that their angles are congruent.
To fully understand this definition, you have to know what corresponding angles and corresponding sides mean. Here’s the lowdown on corresponding. In Figure 8-1, if you expand ABCD to the same size as WXYZ and slide it to the right, it’d stack perfectly on top of WXYZ. A would stack on W, B on X, C on Y, and D on Z. These vertices are thus corresponding. And therefore, you say that ![]() corresponds to
corresponds to ![]() ,
, ![]() corresponds to
corresponds to ![]() , and so on. Also, side
, and so on. Also, side ![]() corresponds to side
corresponds to side ![]() ,
, ![]() to
to ![]() , and so on.
, and so on.
Now I’ll use quadrilaterals ABCD and WXYZ to explore the definition of similar polygons in greater depth:
- Corresponding angles are congruent. You can see that
 and
and  are both
are both  and thus congruent,
and thus congruent,  , and so on. When you blow up or shrink a figure, the angles don’t change.
, and so on. When you blow up or shrink a figure, the angles don’t change. - Corresponding sides are proportional. The ratios of corresponding sides are equal, like this:

- Each ratio equals 10, the expansion factor. (If the ratios were flipped upside down — which is equally valid — each would equal
 , the shrink factor.) And not only do these ratios all equal 10, but the ratio of the perimeters of ABCD and WXYZ also equals 10.
, the shrink factor.) And not only do these ratios all equal 10, but the ratio of the perimeters of ABCD and WXYZ also equals 10.
How similar figures line up
Two similar figures can be positioned so that they either line up or don’t line up. You can see that figures ABCD and WXYZ in Figure 8-1 are positioned in the same way in the sense that if you were to blow up ABCD to the size of WXYZ and then slide ABCD over, it’d match up perfectly with WXYZ. Now check out Figure 8-2, which shows ABCD again with another similar quadrilateral. You can easily see that, unlike the quadrilaterals in Figure 8-1, ABCD and PQRS are not positioned in the same way.

FIGURE 8-2: Similar quadrilaterals that aren’t lined up.
In the preceding section, you see how to set up a proportion for similar figures using the positions of their sides, which I’ve labeled left side, right side, top, and base — for example, one valid proportion is ![]() . This is a good way to think about how proportions work with similar figures, but this works only if the figures are drawn like ABCD and WXYZ are. When similar figures are drawn facing different ways, as in Figure 8-2, the left side doesn’t necessarily correspond to the left side, and so on, and you have to take greater care that you’re pairing up the proper vertices and sides.
. This is a good way to think about how proportions work with similar figures, but this works only if the figures are drawn like ABCD and WXYZ are. When similar figures are drawn facing different ways, as in Figure 8-2, the left side doesn’t necessarily correspond to the left side, and so on, and you have to take greater care that you’re pairing up the proper vertices and sides.
Quadrilaterals ABCD and PQRS are similar, but you can’t say that ![]() because the vertices don’t pair up in this order. Ignoring its size, PQRS is the mirror image of ABCD. If you flip PQRS over in the left-right direction, you get the image in Figure 8-3.
because the vertices don’t pair up in this order. Ignoring its size, PQRS is the mirror image of ABCD. If you flip PQRS over in the left-right direction, you get the image in Figure 8-3.

FIGURE 8-3: Flipping PQRS over to make SRQP lines it up nicely with ABCD — pure poetry!
Now it’s easier to see how the vertices pair up. A corresponds to S, B with R, and so on, so you write the similarity like this: ![]() .
.
Solving a similarity problem
Enough of this general stuff — let’s see these ideas in action:

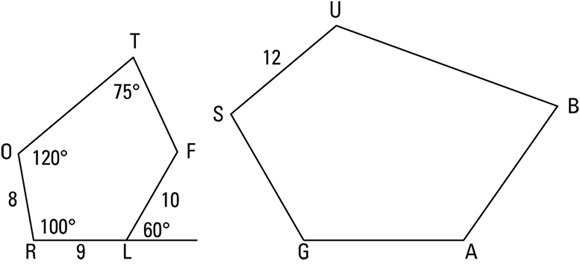
You can see that the ROTFL and SUBAG aren’t positioned the same way just by looking at the figure (and noting that their first letters, R and S, aren’t in the same place). So you need to make sure you pair up their vertices correctly, but that’s a snap because the letters in ![]() show you what corresponds to what. R corresponds to S, O corresponds to U, and so on. (By the way, do you see what you’d have to do to line up SUBAG with ROTFL? SUBAG has sort of been tipped over to the right, so you’d have to rotate it counterclockwise a bit and stand it up on base
show you what corresponds to what. R corresponds to S, O corresponds to U, and so on. (By the way, do you see what you’d have to do to line up SUBAG with ROTFL? SUBAG has sort of been tipped over to the right, so you’d have to rotate it counterclockwise a bit and stand it up on base ![]() . You may want to redraw SUBAG like that, which can really help you see how all the parts of the two pentagons correspond.)
. You may want to redraw SUBAG like that, which can really help you see how all the parts of the two pentagons correspond.)
Find the lengths of
 and
and 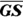 .
.The order of the vertices in
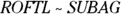 tells you that
tells you that  corresponds to
corresponds to  and that
and that 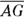 corresponds to
corresponds to  ; thus, you can set up the following proportion to find missing length
; thus, you can set up the following proportion to find missing length  :
: 
This method of setting up a proportion and solving for the unknown length is the standard way of solving this type of problem. It’s often useful, and you should know how to do it.
But another method can come in handy. Here’s how to use it to find
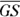 : Divide the lengths of two known sides of the figures like this:
: Divide the lengths of two known sides of the figures like this: 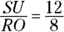 , which equals 1.5. That answer tells you that all the sides of SUBAG (and its perimeter) are 1.5 times as long as their counterparts in ROTFL. The order of the vertices in
, which equals 1.5. That answer tells you that all the sides of SUBAG (and its perimeter) are 1.5 times as long as their counterparts in ROTFL. The order of the vertices in 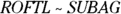 tells you that
tells you that  corresponds to
corresponds to  ; thus,
; thus,  is 1.5 times as long as
is 1.5 times as long as 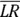 :
: 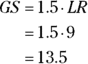
Find the perimeter of SUBAG.
The method I just introduced tells you that

Find the measures of
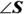 ,
,  , and
, and  .
.S corresponds to R, G corresponds to L, and A corresponds to F, so
- Angle S is the same as
 , or
, or  .
. - Angle G is the same as
 , which is
, which is  (the supplement of the
(the supplement of the  angle).
angle).
To get
 , you first have to find
, you first have to find 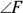 with the sum-of-angles formula:
with the sum-of-angles formula: 
Because the other four angles of ROTFL (clockwise from L) add up to
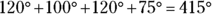 ,
,  , and therefore
, and therefore  , must equal
, must equal 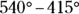 , or
, or 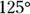 .
.- Angle S is the same as
Proving Triangles Similar
Chapter 5 explains five ways to prove triangles congruent: SSS, SAS, ASA, AAS, and HLR. Here, I show you the three ways to prove triangles similar: AA, SSS~, and SAS~.
- AA: If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.
- SSS~: If the ratios of the three pairs of corresponding sides of two triangles are equal, then the triangles are similar.
- SAS~: If the ratios of two pairs of corresponding sides of two triangles are equal and the included angles are congruent, then the triangles are similar.
Tackling an AA proof
The AA method is the most frequently used and is therefore the most important. Luckily, it’s also the easiest of the three methods to use. Give it a whirl with the following proof:

Here’s a possible game plan (this hypothetical thought process assumes that you don’t know that this is an AA proof from the title of this section): The first given is about angles, and the second given is about parallel lines, which will probably tell you something about congruent angles. Therefore, this proof is almost certainly an AA proof. So all you have to do is think about the givens and figure out which two pairs of angles you can prove congruent to use for AA. Duck soup.
Take a look at how the proof plays out:

Using SSS~
The upcoming SSS~ proof incorporates the Midline Theorem.
- One-half the length of the third side, and
- Parallel to the third side.
Check out this theorem in action with an SSS~ proof:

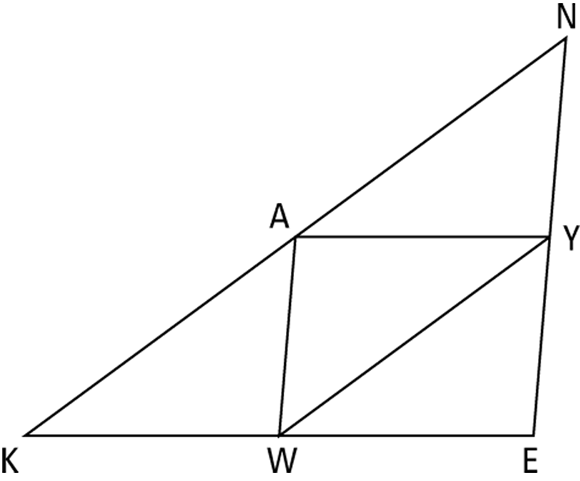
Use the first part of the Midline Theorem to prove that
 .
.The first part of the Midline Theorem says that a segment connecting the midpoints of two sides of a triangle is half the length of the third side. You have three such segments:
 is half the length of
is half the length of  ,
,  is half the length of
is half the length of 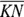 , and
, and 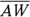 is half the length of
is half the length of  . That gives you the proportionality you need:
. That gives you the proportionality you need: . Thus, the triangles are similar by SSS~.
. Thus, the triangles are similar by SSS~.Use part two of the Midline Theorem to prove that
 .
.The second part of the Midline Theorem tells you that a segment connecting the midpoints of two sides of a triangle is parallel to the third side. You have three segments like this,
 ,
,  , and
, and 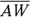 , each of which is parallel to a side of
, each of which is parallel to a side of  . The pairs of parallel segments should make you think about using the parallel-line theorems, which could give you the congruent angles you need to prove the triangles similar with AA.
. The pairs of parallel segments should make you think about using the parallel-line theorems, which could give you the congruent angles you need to prove the triangles similar with AA.Look at parallel segments
 and
and 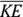 , with transversal
, with transversal 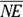 . You can see that
. You can see that  is congruent to
is congruent to  because corresponding angles (the parallel-line meaning of corresponding angles) are congruent.
because corresponding angles (the parallel-line meaning of corresponding angles) are congruent.Now look at parallel segments
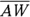 and
and 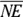 , with transversal
, with transversal  . Angle AYN is congruent to
. Angle AYN is congruent to 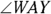 because they’re alternate interior angles. So by the Transitive Property,
because they’re alternate interior angles. So by the Transitive Property,  .
.With identical reasoning, you show that
 or that
or that  . The end. The triangles are similar by AA.
. The end. The triangles are similar by AA.
An SAS~ proof


Game Plan: Your thinking might go like this. You have one pair of congruent angles, the vertical angles ![]() and
and ![]() . But it doesn’t look like you can get another pair of congruent angles, so the AA approach is out. What other method can you try? You’re given side lengths in the figure, so the combination of angles and sides should make you think of SAS~. To prove
. But it doesn’t look like you can get another pair of congruent angles, so the AA approach is out. What other method can you try? You’re given side lengths in the figure, so the combination of angles and sides should make you think of SAS~. To prove ![]() with SAS~, you need to find the length of
with SAS~, you need to find the length of ![]() so you can show that
so you can show that ![]() and
and ![]() (the sides that make up
(the sides that make up ![]() ) are proportional to
) are proportional to ![]() and
and ![]() (the sides that make up
(the sides that make up ![]() ). To find
). To find ![]() , you can use the similarity in the given.
, you can use the similarity in the given.
So you begin solving the problem by figuring out the length of ![]() .
. ![]() , so — paying attention to the order of the letters — you see that
, so — paying attention to the order of the letters — you see that ![]() corresponds to
corresponds to ![]() and that
and that ![]() corresponds to
corresponds to ![]() . Thus, you can set up this proportion:
. Thus, you can set up this proportion:

Now, to prove ![]() with SAS~, you use the congruent vertical angles and then check that the following proportion works:
with SAS~, you use the congruent vertical angles and then check that the following proportion works:

This checks. You’re done. (By the way, these fractions both reduce to ![]() , so
, so ![]() is
is ![]() as big as
as big as ![]() .)
.)
Splitting Right Triangles with the Altitude-on-Hypotenuse Theorem
In a right triangle, the altitude that’s perpendicular to the hypotenuse has a special property: It creates two smaller right triangles that are both similar to the original right triangle.
- The two triangles formed are similar to the given triangle and to each other:
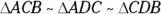
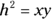 , and
, and and
and 
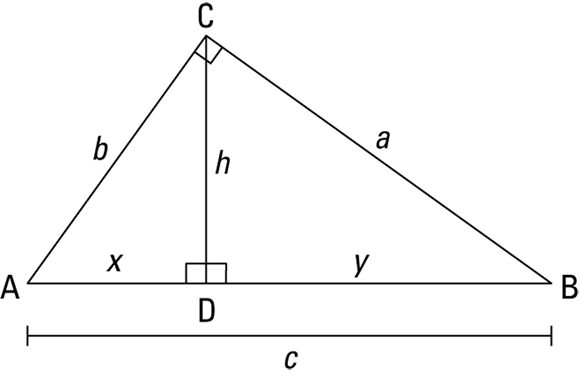
FIGURE 8-4: Three similar right triangles: small, medium, and large.
Use Figure 8-5 to answer the following questions.

FIGURE 8-5: Altitude  lets you apply the Altitude-on-Hypotenuse Theorem.
lets you apply the Altitude-on-Hypotenuse Theorem.
If ![]() and
and ![]() , what’s JM?
, what’s JM?
Set JM equal to x; then use part three of the theorem.

You know that a length can’t be ![]() , so
, so ![]() .
.
The next question illustrates this tip: If ![]() and
and ![]() , how long is KM?
, how long is KM?
First get JL with the Pythagorean Theorem or by noticing that you have a triangle in the 3 : 4 : 5 family — namely a 9-12-15 triangle. So ![]() . Now you could finish with the Altitude-on-Hypotenuse Theorem, but that approach is a bit complicated. Instead, just use an ordinary similar-triangle proportion:
. Now you could finish with the Altitude-on-Hypotenuse Theorem, but that approach is a bit complicated. Instead, just use an ordinary similar-triangle proportion:
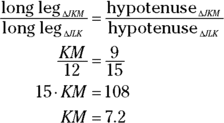
More Proportionality Theorems
In this section, you get two more theorems that, like similar polygons, involve proportions.
The Side-Splitter Theorem
The Side-Splitter Theorem isn’t really necessary because the problems in which you use it involve similar triangles, so you can solve them with the ordinary similar-triangle proportions from earlier in this chapter. The Side-Splitter Theorem just gives you an alternative, shortcut solution method.
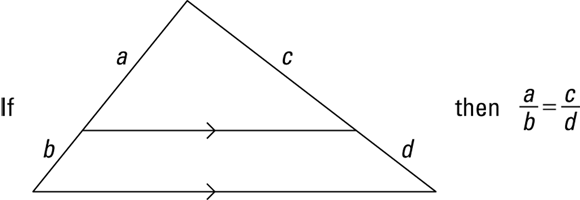
FIGURE 8-6: A line parallel to a side cuts the other two sides proportionally.

Because ![]() , you use the Side-Splitter Theorem to get x:
, you use the Side-Splitter Theorem to get x:
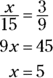
Now find y: First, don’t fall for the trap and conclude that ![]() . This is a doubly sneaky trap that I’m especially proud of. Side y looks like it should equal 4 for two reasons: First, you could jump to the erroneous conclusion that
. This is a doubly sneaky trap that I’m especially proud of. Side y looks like it should equal 4 for two reasons: First, you could jump to the erroneous conclusion that ![]() is a 3-4-5 right triangle. But nothing tells you that
is a 3-4-5 right triangle. But nothing tells you that ![]() is a right angle, so you can’t conclude that.
is a right angle, so you can’t conclude that.
Second, when you see the ratios of 9 : 3 (along ![]() ) and 15 : 5 (along
) and 15 : 5 (along ![]() , after solving for x), both of which reduce to 3 : 1, it looks like PQ and y should be in the same 3 : 1 ratio. That would make PQ : y a 12 : 4 ratio, which again leads to the wrong answer that y is 4. The answer comes out wrong because this thought process amounts to using the Side-Splitter Theorem for the sides that aren’t split — which you aren’t allowed to do.
, after solving for x), both of which reduce to 3 : 1, it looks like PQ and y should be in the same 3 : 1 ratio. That would make PQ : y a 12 : 4 ratio, which again leads to the wrong answer that y is 4. The answer comes out wrong because this thought process amounts to using the Side-Splitter Theorem for the sides that aren’t split — which you aren’t allowed to do.
So finally, the correct way to get y is to use an ordinary similar-triangle proportion. The triangles in this problem are positioned the same way, so you can write the following:
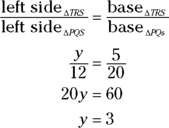
The Angle-Bisector Theorem
In this final section, you get another theorem involving a proportion; but unlike everything else in this chapter, this theorem has nothing to do with similarity.

FIGURE 8-7: Because the angle is bisected, segments c and d are proportional to sides a and b.
How about an angle-bisector problem? Why? Oh, just BCUZ.
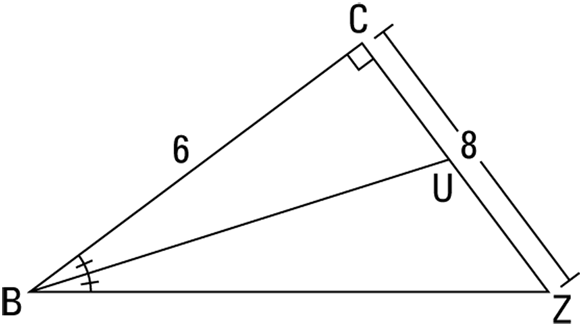
You get BZ with the Pythagorean Theorem ![]() or by noticing that
or by noticing that ![]() is in the 3 : 4 : 5 family. It’s a 6-8-10 triangle, so BZ is 10.
is in the 3 : 4 : 5 family. It’s a 6-8-10 triangle, so BZ is 10.
Next, set CU equal to x; this makes UZ equal to ![]() . Set up the angle-bisector proportion and solve for x:
. Set up the angle-bisector proportion and solve for x:
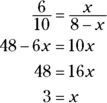
So CU is 3 and UZ is 5.
The Pythagorean Theorem then gives you BU:


 Similar polygons: For two polygons to be similar, both of the following must be true:
Similar polygons: For two polygons to be similar, both of the following must be true:  Align similar polygons. If you get a problem with a diagram of similar polygons that aren’t lined up, consider redrawing one of them so that they’re both positioned in the same way. This may make the problem easier to solve.
Align similar polygons. If you get a problem with a diagram of similar polygons that aren’t lined up, consider redrawing one of them so that they’re both positioned in the same way. This may make the problem easier to solve. Use the following methods to prove triangles similar:
Use the following methods to prove triangles similar:  Don’t use the Side-Splitter Theorem on sides that aren’t split. You can use the Side-Splitter Theorem only for the four segments on the split sides of the triangle. Do not use it for the parallel sides, which are in a different ratio. For the parallel sides, use similar-triangle proportions. (Whenever a triangle is divided by a line parallel to one of its sides, the smaller triangle created is similar to the original, larger triangle.)
Don’t use the Side-Splitter Theorem on sides that aren’t split. You can use the Side-Splitter Theorem only for the four segments on the split sides of the triangle. Do not use it for the parallel sides, which are in a different ratio. For the parallel sides, use similar-triangle proportions. (Whenever a triangle is divided by a line parallel to one of its sides, the smaller triangle created is similar to the original, larger triangle.)