Chapter 9
Circle Basics
IN THIS CHAPTER
Defining radii, chords, and arcs
Theorizing about the angle-arc theorems
Practicing products with the power theorems
In a sense, the circle is the simplest of all shapes: no corners, no irregularities, the same simple shape no matter how you turn it. On the other hand, that simple curve involves the number pi 
, and nothing’s simple about that. It goes on forever with no repeating pattern of digits. Despite the fact that mathematicians have been studying the circle and the number 
for over 2,000 years, many unsolved mysteries about them remain. Let’s get started looking at this fascinating shape.
Radii, Chords, and Diameters
Why don’t we begin with the three main types of line segments inside a circle: radii, chords, and diameters:
- Radius: A circle’s radius is the distance from its center to a point on the circle. In addition to being a measure of distance, a radius is also a segment that goes from a circle’s center to a point on the circle.
- Chord: A segment that connects two points on a circle.
- Diameter: A chord that passes through a circle’s center. A circle’s diameter is twice as long as its radius.
Five circle theorems
I hope you have some available space on your mental hard drive for more theorems. (If not, maybe you can free up some room by deleting a few not-so-useful facts such as the date of the Battle of Hastings: A.D. 1066.)
Radii size: All radii of a circle are congruent.- Perpendicularity and bisected chords:
- If a radius is perpendicular to a chord, then it bisects the chord.
- If a radius bisects a chord (that isn’t a diameter), then it’s perpendicular to the chord.
- Distance and chord size:
- If two chords of a circle are equidistant from the center of the circle, then they’re congruent.
- If two chords of a circle are congruent, then they’re equidistant from its center.
Using extra radii
In real estate, the three most important factors are location, location, location. With circles, it’s radii, radii, radii. In circle problems, you’ll often need to add radii and partial radii to create right triangles or isosceles triangles that you can then use to solve the problem.
- Draw additional radii on the figure. You should draw radii to points where something else intersects or touches the circle, as opposed to just any old point on the circle.
- Open your eyes and notice all the radii, including new ones you’ve drawn, and mark them all congruent. For some odd reason, people often fail to notice all the radii in a problem or fail to note that they’re congruent.
- Draw in the segment (part of a radius) that goes from the center of a circle to a chord and that’s perpendicular to the chord. This segment bisects the chord.
Let’s do a problem: Find the area of inscribed quadrilateral GHJK shown on the left. The circle has a radius of 2.
The tip above gives you two hints for this problem. The first is to draw in the four radii to the four vertices of the quadrilateral as shown in the figure on the right.
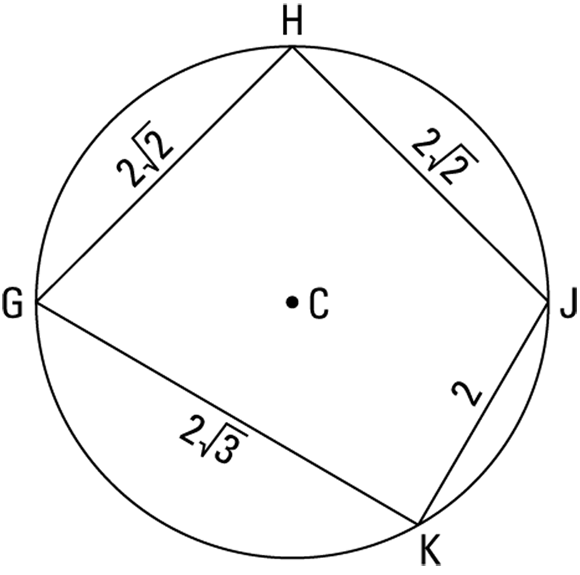
Now you simply need to find the area of the individual triangles. You can see that 
is equilateral, so you can use the equilateral triangle formula for this one:
And if you’re on the ball, you should recognize triangles GHC and HJC. Their sides are in the ratio of 
, which reduces to 
; thus, they’re 
right triangles. The two legs of a right triangle can be used for its base and height, so getting their areas is a snap. For each triangle,
Another hint from the tip helps you with 
. Draw its altitude (a partial radius) from C to 
. This radius is perpendicular to 
and thus bisects 
into two segments of length 
. You’ve divided 
into two right triangles; each has a hypotenuse of 2 and a leg of 
, so the other leg (the altitude) is 1 (by the Pythagorean Theorem or by recognizing that these are 
triangles whose sides are in the ratio of 
). So 
has an altitude of 1 and a base of 
. Just use the regular area formula again:
Now just add ’em up:
Arcs and Central Angles
This section covers arcs and central angles. Big surprise!
Arc: An arc is simply a curved piece of a circle. Any two points on a circle divide the circle into two arcs: a minor arc (the smaller piece) and a major arc (the larger) — unless the points are the endpoints of a diameter, in which case both arcs are semicircles. Figure 9-1 shows minor arc 
(a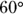 
arc) and major arc 
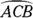(a 
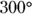arc).Central angle: A central angle is an angle whose vertex is at the center of a circle. The sides of a central angle are radii that hit the circle at the opposite ends of an arc — or as mathematicians say, the angle intercepts the arc.
The measure of an arc is the same as the degree measure of the central angle that intercepts it. The figure shows central angle
, which, like 
, measures 
.
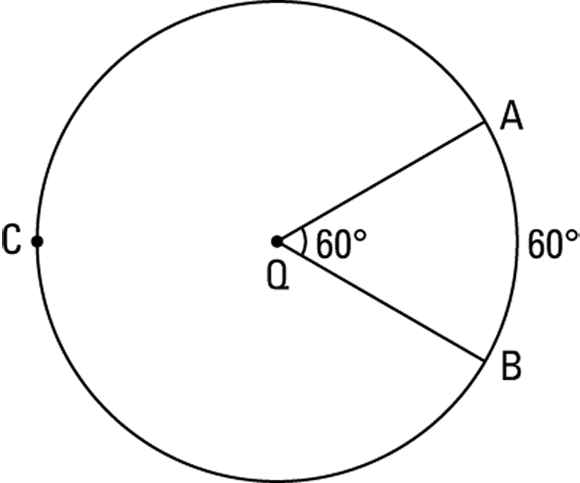
FIGURE 9-1: A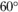 
central angle cuts out a 
arc.
Tangents
This section covers — can you guess? — tangent lines. A line is tangent to a circle if it touches it at one and only one point.
Radius-tangent perpendicularity: If a line is tangent to a circle, then it is perpendicular to the radius drawn to the point of tangency.
Don’t neglect to check circle problems for tangent lines and the right angles that occur at points of tangency. You may have to draw in one or more radii to points of tangency to create the right angles. The right angles often become parts of right triangles (or sometimes rectangles).
Here’s an example problem: Find the radius of circle C and the length of 
in the following figure.
When you see a circle problem, you should be saying to yourself: radii, radii, radii! So draw in radius 
, which, according to the above theorem, is perpendicular to 
. Set it equal to x, which gives 
a length of x as well. You now have right triangle 
, so use the Pythagorean Theorem to find x:
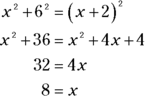
So the radius is 8. Then you can see that 
is an 8-15-17 triangle, so CE is 17. (Of course, you can also get CE with the Pythagorean Theorem.) CD is 8 (and it’s the third radius in this problem; does radii, radii, radii ring a bell?). Therefore, DE is 
, or 9. That does it.
The Pizza Slice Formulas
In this section, you begin with the formulas for a circle’s area and circumference. Then you use those formulas to compute lengths, perimeters, and areas of various parts of a circle.
Circumference and area of a circle:
Determining arc length
Before getting to the arc length formula, I want to mention a potential source of confusion about arcs. Earlier in this chapter, the measure of an arc is defined as the degree measure of the central angle that intercepts the arc. But in this section, I go over the length of an arc. In this context, length means the same commonsense thing length always means — you know, like the length of a piece of string. (With an arc, of course, it’d be a curved piece of string.) In a nutshell, the measure of an arc is the degree size of its central angle; the length of an arc is the regular length along the arc.
A circle is 
all the way around; therefore, if you divide an arc’s degree measure by 
, you find the fraction of the circle’s circumference that the arc makes up. Then, if you multiply the length of the circumference by that fraction, you get the length along the arc.
Arc length: The length of an arc is equal to the circumference of the circle 
times the fraction of the circle represented by the arc’s measure (note that the degree measure of an arc is written like 
):
See Figure 9-2 for an example.
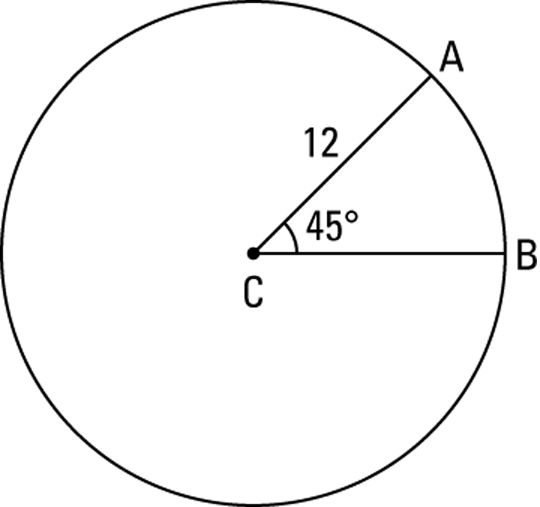
FIGURE 9-2: Arc 
is 
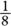of the circle’s circumference.
Check out the calculations for 
. Its degree measure is 
and the radius of the circle is 12, so here’s the math for its length:
As you can see, because 
is 
of 
, the length of arc 
is 
of the circumference of 
.
Sector and segment area
In this section, I cover sector and segment area.
- Sector: A region bounded by two radii and an arc of a circle. (Plain English: the shape of a piece of pizza.)
- Segment of a circle: A region bounded by a chord and an arc of a circle.
Just as an arc is a fraction of a circle’s circumference, a sector is a fraction of a circle’s area; so computing the area of a sector works exactly like the arc-length formula.
Area of a sector: The area of a sector (such as sector PQR in Figure 9-3) is equal to the area of the circle 
times the fraction of the circle represented by the sector:
FIGURE 9-3: A pizza-slice sector and a segment of a circle.
Look back to Figure 9-2. When you do the math with the above formula, you’ll see that because 
is 
of 
, the area of sector ACB is 
of the area of the circle (just like the length of 
is 
of the circle’s circumference).
Area of a segment: To compute the area of a segment like the one in Figure 9-3, just subtract the area of the triangle from the area of the sector (by the way, there’s no technical way to name segments, but let’s call this one circle segment XZ):
We just covered how to compute the area of a sector. To get the triangle’s area, you draw an altitude that goes from the circle’s center to the chord that makes up the triangle’s base. This altitude is a leg of a right triangle whose hypotenuse is a radius of the circle. You finish with right-triangle ideas such as the Pythagorean Theorem. You see this in the next problem.
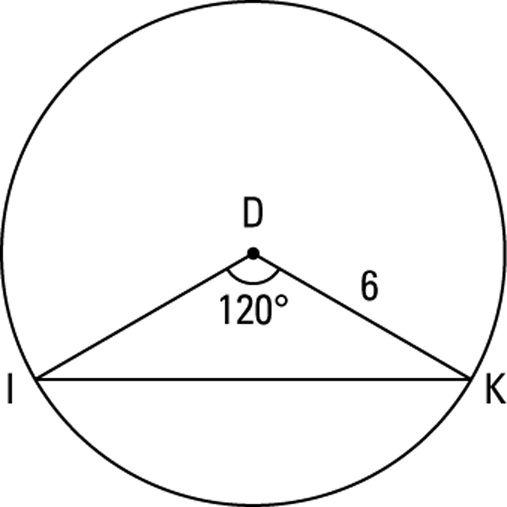
Find the length of arc
.The measure of the arc is
, which is a third of 
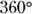, so the length of 
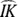is a third of the circumference. That’s all there is to it. Here’s how this looks when you plug it into the formula: 
Find the area of sector IDK.
Because
takes up a third of the degrees in a circle, sector IDK occupies a third of the circle’s area. 
Find the area of circle segment IK.
To get this, you need the area of
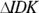so you can subtract it from the area of sector IDK. Draw an altitude straight down from D to 
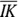. That creates two 
triangles. The sides of a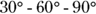 
triangle are in the ratio of 
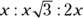. In this problem, the hypotenuse is 6, so the altitude (the short leg) is half of that, or 3, and the base (the long leg) is 
. 
is twice as long as the base of the 
triangle, so it’s twice 
, or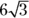 
. You finish with the segment area formula: 
The Angle-Arc Formulas
This section looks at angles that intersect a circle. The vertices of these angles can lie inside the circle, on the circle, or outside the circle. The formulas in this section tell you how these angles are related to the arcs they intercept.
Angles on a circle
Of the three places an angle’s vertex can be in relation to a circle, the angles whose vertices lie on a circle are the ones that come up in the most problems and are therefore the most important. These angles come in two flavors:
- Inscribed angle: An inscribed angle, like
in Figure 9-4a, is an angle whose vertex lies on a circle and whose sides are two chords of the circle. - Tangent-chord angle: A tangent-chord angle, like
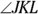in Figure 9-4b, is an angle whose vertex lies on a circle and whose sides are a tangent and a chord of the circle.
FIGURE 9-4: Angles with vertices on a circle.
Measure of an angle on a circle: The measure of an inscribed angle or a tangent-chord angle is one-half the measure of its intercepted arc.
For example, in Figure 9-4, 
and 
.
Make sure you remember the simple idea that an angle on a circle is half the measure of the arc it intercepts. If you forget which is half of which, try this: Draw a quick sketch of a circle with a 
arc (a quarter of the circle) and an inscribed angle that intercepts the 
arc. You’ll see right away that the angle is less than 
, telling you that the angle is the thing that’s half of the arc, not vice versa.
Angles inside a circle
Measure of an angle inside a circle: The measure of an angle whose vertex is inside a circle (a chord-chord angle) is one-half the sum of the measures of the arcs intercepted by the angle and its vertical angle. Check out Figure 9-5, which shows you chord-chord angle SVT. You find the measure of the angle like this:
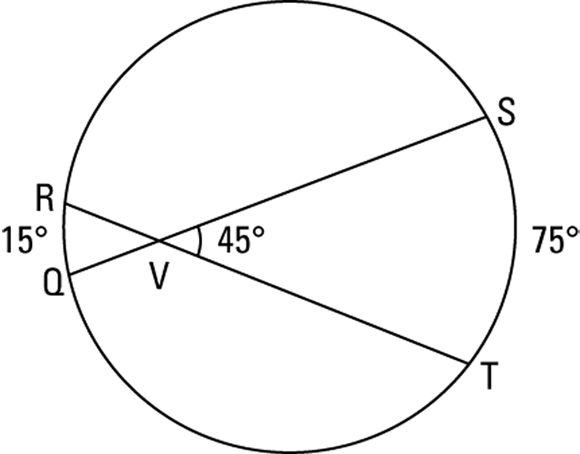
FIGURE 9-5: Chord-chord angles are inside a circle.
Angles outside a circle
Three varieties of angles fall outside a circle, and all are made up of tangents and secants. You know what a tangent is, and here’s the definition of secant.
Technically, a secant is a line that intersects a circle at two points. But the secants you use in this section are segments that cut through a circle and that have one endpoint outside the circle and one endpoint on the circle.
So here are the three types of angles that are outside a circle (see Figure 9-6):
- Secant-secant angle: A secant-secant angle, like
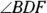in Figure 9-6a, is an angle whose vertex lies outside a circle and whose sides are two secants. - Secant-tangent angle: A secant-tangent angle, like
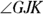in Figure 9-6b, is an angle whose vertex lies outside a circle and whose sides are a secant and a tangent. - Tangent-tangent angle: A tangent-tangent angle, like
in Figure 9-6c, is an angle whose vertex lies outside a circle and whose sides are two tangents.
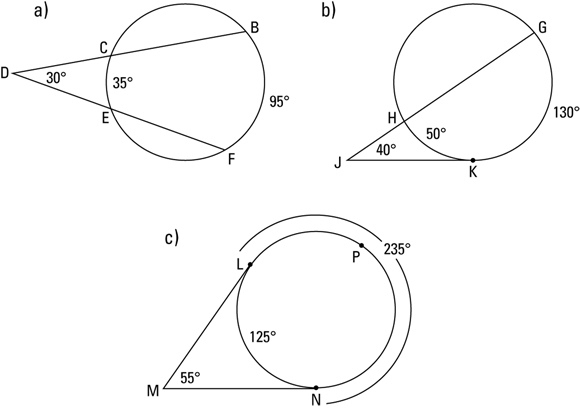
FIGURE 9-6: Three kinds of angles outside a circle.
Measure of an angle outside a circle: The measure of a secant-secant angle, a secant-tangent angle, or a tangent-tangent angle is one-half the difference of the measures of the intercepted arcs. For example, in Figure 9-6,
Note that you should subtract the smaller arc from the larger. (If you get a negative answer, you subtracted the wrong way.)
Keeping the formulas straight
In the previous three sections, you see six types of angles made up of chords, secants, and tangents but only three angle-arc formulas. As you can tell from the titles of the sections, to determine which of the three angle-arc formulas you need to use, all you need to pay attention to is where the angle’s vertex is: inside, on, or outside the circle. You don’t have to worry about whether the two sides of the angle are chords, tangents, secants, or some combination of these things.
The next tip can help you remember which formula goes with which category of angle. First, check out Figure 9-7.
FIGURE 9-7: As the angle gets farther from the center of the circle, it gets smaller.
You can see that the small angle, 
(maybe about 
), is outside the circle; the medium angle, 
(about 
), is on the circle; and the large angle, 
(roughly 
), is inside the circle. Here’s one way to understand why the sizes of the angles go in this order. Say that the sides of 
are elastic. Picture grabbing 
at its vertex and pulling it to the left (as its ends remain attached to A and B). The farther you pull 
to the left, the smaller the angle would get.
Subtracting makes things smaller, and adding makes things larger, right? So here’s how to remember which angle-arc formula to use (see Figure 9-7 and Figures 9-4, 9-5, and 9-6):
- To get the small angle, you subtract:
. - To get the medium angle, you do nothing:
. - To get the large angle, you add:
.
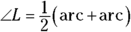(Note: For the third bullet above, you have to look at Figure 9-5 to see both arcs; adding the second arc for angle L in Figure 9-7 would have made the figure look too messy.)
The Power Theorems
Like the preceding sections, this section takes a look at what happens when angles and circles intersect. But this time, instead of analyzing the size of angles and arcs, you analyze the lengths of the segments that make up the angles.
The Chord-Chord Theorem
The Chord-Chord Power Theorem was brilliantly named for the fact that the theorem uses a chord and … . another chord!
Chord-Chord Power Theorem: If two chords of a circle intersect, then the product of the measures of the parts of one chord is equal to the product of the measures of the parts of the other chord. (Whew, what a mouthful!)
Try out your power-theorem skills on this problem:
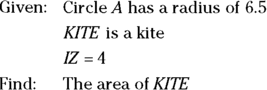
To get the kite’s area, you need the lengths of its diagonals. The diagonals are two chords that cross each other, so you should consider using the Chord-Chord Power Theorem.
But first, note that diagonal 
is the circle’s diameter. Circle A has a radius of 6.5, so its diameter is twice as long, or 13, and thus that’s the length of diagonal 
. Then you see that ZE must be 
, or 9. Now you have two of the lengths, 
and 
, for the segments you use in the theorem:
Because KITE is a kite, diagonal 
bisects diagonal 
. Thus, 
, so you can set them both equal to x. Plug everything into the equation:
You can obviously reject 
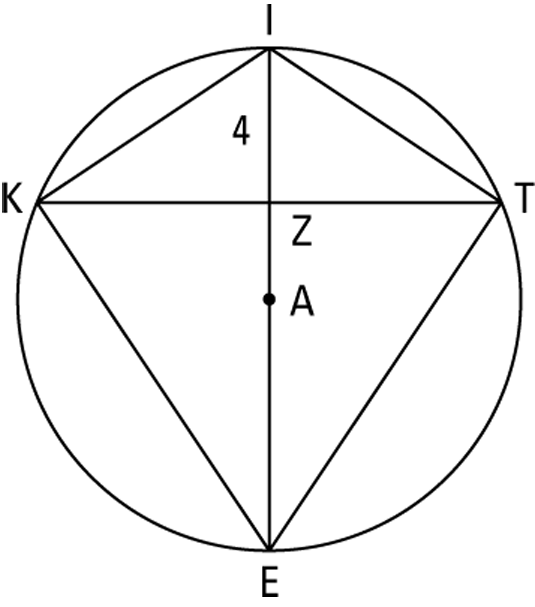
as a length, so x is 6. KZ and ZT are thus both 6, and diagonal 
is therefore 12. You’ve already figured out that the length of the other diagonal is 13, so now you finish with the kite area formula:
The Tangent-Secant Theorem
Now let’s move on to the Tangent-Secant Power Theorem — another awe-inspiring example of creative nomenclature.
Tangent-Secant Power Theorem: If a tangent and a secant are drawn from an external point to a circle, then the square of the measure of the tangent is equal to the product of the measures of the secant’s external part and the entire secant. (Another mouthful!)
For example, in Figure 9-8, 
.
FIGURE 9-8: The Tangent-Secant Power Theorem: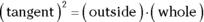 
.
The Secant-Secant Theorem
Last but not least, I give you the Secant-Secant Power Theorem. Are you sitting down? This theorem involves two secants! (If you’re trying to come up with a creative name for your child like Dweezil or Moon Unit, talk to Frank Zappa, not the guy who named the power theorems.)
Secant-Secant Power Theorem: If two secants are drawn from an external point to a circle, then the product of the measures of one secant’s external part and that entire secant is equal to the product of the measures of the other secant’s external part and that entire secant.
For instance, in Figure 9-9, 
.
FIGURE 9-9: The Secant-Secant Power Theorem: 
.
Condensing the power theorems into a single idea
All three of the power theorems involve an equation with a product of two lengths (or one length squared) that equals another product of lengths. And each length is a distance from the vertex of an angle to the edge of the circle. Thus, all three theorems use the same scheme:
This unifying scheme can help you remember all three of the theorems I discuss in the preceding sections. And it’ll help you avoid the common mistake of multiplying the external part of a secant by its internal part (instead of correctly multiplying the external part by the entire secant) when you’re using the Tangent-Secant Theorem or the Secant-Secant Power Theorem.