8.2.1 Tree-Building Algorithms

Tree-building methods result in a model that can be thought of as a patchwork of constant predictors. The differences among decision tree (DT) methods revolve around (1) how they break down the entire space of the data into smaller and smaller regions and (2) when they stop the breakdown. Here’s how a decision tree classifier (DTC) breaks down the iris data when it only considers the first two features (sepal length and sepal width):

In [2]:

Click here to view code image

tree_classifiers = {'DTC' : tree.DecisionTreeClassifier(max_depth=3)}

fig, ax = plt.subplots(1,1,figsize=(4,3))
for name, mod in tree_classifiers.items():
    # plot_boundary only uses specified columns
    # [0,1] [sepal len/width] to predict and graph
    plot_boundary(ax, iris.data, iris.target, mod, [0,1])
    ax.set_title(name)
plt.tight_layout()

The red region (on the right) is setosa. The blue (top left) and gray (lower center) are the two v classes. Note that the boundaries are all made with lines that are parallel to the x or y axes. Also, I’m sneaking in a max_depth=3 argument to the DT constructor. We’ll go into more detail on that shortly. For now, max_depth is simply the maximum number of questions I can ask of any example before I classify it. You might remember playing a game called Twenty Questions. That’s a bit like a max_depth=20 constraint.

Breaking up the whole space creates a partition. We predict the class of an example based on the color of the region the example falls into. Mathematically, we can write

That equation is a bit of symbol-soup. I would apologize for showing it, but I want to take a few sentences to convince you that it is a very odd-looking dot product. Here goes. Let’s start by defining the letters. R is a region of our graph; P is the group of all of the regions. Summing over all of the R ∊ P means that we add up some values over the whole graph. c_R is the predicted class for the region R: for example, one of the types of irises. I is an indicator function which gives us a value of one if an example is in R and zero otherwise. Taken together, c_R and I(example ∊ R) give us c_R when an example is in R and give us zero everywhere else. Together, these pieces look like Σc_RI which is exactly a pretty convoluted dot product.

Trees create blocky—think Legos or Tetris—regions of colored space from our features. The partition—the shapes of the regions—is pretty constrained from one point of view. It is made of overlaid rectangles where only the topmost rectangle counts. Overlaying cards as in Figure 8.4 gives us boundaries like those in Figure 8.5. You can imagine neatly spreading out a few decks of cards on a rectangular table. The cards are of different sizes and they must be horizontally and vertically aligned with the sides of the table. The cards can overlap. When cards of the same suit (clubs, hearts, diamonds, spades) are touching one another, they form a larger region for that suit. To create those regions from points in space, we create simple yes/no answers by thresholding. For example, we test a feature Temp against a value 55. Choosing the values to split on is the trickiest aspect of implementing decision trees by hand.

There are a number of major tree-building algorithms. ID3, C4.5, and C5.0 were made by Quinlan. CART was developed independently. In general, the tree-building algorithms use the following steps:

1. Evalute the set of features and splits and pick a “best” feature-and-split.

2. Add a node to the tree that represents the feature-split.

3. For each descendant, work with the matching data and either:

   (1) If the targets are similar enough, return a predicted target.

   (2) If not, return to step 1 and repeat.

Each of these steps can be implemented and limited in different ways. The DT algorithms control (1) what splits and partitions are allowed, (2) how feature-splits are evaluated, (3) what makes targets in a group similar enough to form a leaf, and (4) other limits. The other limits commonly include an absolute limit on the depth of the tree and the minimum number of examples at a leaf to make a prediction, regardless of similarity. These constraints help prevent overfitting. As with identifying labels, if we can continually break down the feature space until we have single examples in each bucket, we’ll get perfect training accuracy—but we’ll lose generalization. Unconstrained trees have very little bias, but they do suffer from high variance. We’ll see examples of this shortly.

8.2.2 Let’s Go: Decision Tree Time

We can take a quick look at how trees do on the basic iris dataset.

In [3]:

Click here to view code image

dtc = tree.DecisionTreeClassifier()
skms.cross_val_score(dtc,
                     iris.data, iris.target,
                     cv=3, scoring='accuracy') # sorry

Out[3]:

array([0.9804, 0.9216, 0.9792])

Overall, they do quite well.

If we have a fit tree, we can view it graphically using one of two different methods. The first needs an additional Python library, pydotplus, which you may not have installed on your computer. The second requires an additional command-line program, dot, which you may have to install. dot is a program for drawing diagrams specified by text files, sort of like using HTML to specify how something looks on screen. These outputs have a Gini value listed—I’ll discuss that very briefly at the end of Chapter 13. For now, just think of it as measuring how pure the class split is at that point. If there is only one class represented, the Gini value is 0.0.

We’ll use the simplified single-class iris problem here: it only results in a single split, even if we allow the tree the freedom to grow more deeply.

In [4]:

Click here to view code image

iris_1c_tree = (tree.DecisionTreeClassifier()
                    .fit(iris_1c_train_ftrs, iris_1c_train_tgt))

In [5]:

Click here to view code image

# using an additional library:
# conda install pydotplus
# pip install pydotplus
import pydotplus
dot_data = tree.export_graphviz(iris_1c_tree, out_file=None)
graph = pydotplus.graph_from_dot_data(dot_data)
graph.write_png("outputs/iris_1c.png")
Image("outputs/iris_1c.png", width=75, height=75)

Out[5]:

We can also see what a more complicated tree looks like. Here, I’ll use the other tree drawing method. We’ll specify additional arguments to export_graphviz so we can make the output a bit more presentable.

In [6]:

Click here to view code image

iris_tree = (tree.DecisionTreeClassifier()
                 .fit(iris_train_ftrs, iris_train_tgt))

In [7]:

Click here to view code image

# no added library to produce .dot file
with open("outputs/iris.dot", 'w') as f:
     dot_data = tree.export_graphviz(iris_tree, out_file=f,
                                     feature_names=iris.feature_names,
                                     class_names=iris.target_names,
                                     filled=True, rounded=True)

# the following '!' lines are "shell" commands
# uses the 'dot' program to convert dot -> png
!dot -Tpng outputs/iris.dot -o outputs/iris.png
!rm outputs/iris.dot

Image("outputs/iris.png", width=140, height=140)

Out[7]:

We can also get a feeling for what happens with increasing depth in a decision tree. Let’s take a look at the default tree from DecisionTreeClassifier and trees limited to depths 1, 2, and 3. Remember, even at a max_depth=2, we’ll have three splits: one split for the root node and one split at each of the two children. We expect to see these three splits as three cuts across our feature space. The default setting, max_depth=None, implies not constraining the depth at all, as if max_depth = ∞ (the sideways 8 means infinity).

In [8]:

Click here to view code image

fig, axes = plt.subplots(2,2,figsize=(4,4))

depths = [1, 2, 3, None]
for depth, ax in zip(depths, axes.flat):
    dtc_model = tree.DecisionTreeClassifier(max_depth=depth)
    # plot_boundary only uses specified columns [0,1]
    # so we are only predicting with sepal length and width
    plot_boundary(ax, iris.data, iris.target, dtc_model, [0,1])
    ax.set_title("DTC (max_depth={})".format(dtc_model.max_depth))

plt.tight_layout()

As a sanity check for our intuition about how the tree maps to separation in space, you can look at the top-right figure. Red is on the right, blue is in the top-left, and gray is the remainder. It has the three boundary lines—cuts or divisions—we expect: one between gray and red, one horizontally between gray and blue, and one vertically between gray and blue. The two gray-blue edges come from two different splits. Also, look at how many mini-regions there are in the bottom-right, max_depth=None, figure. Test yourself: as the max depth increases, are we moving towards overfitting or underfitting?

8.2.3 Bias and Variance in Decision Trees

If we start with a wide open, no-depth-limit tree, we’ll have a model that is very flexible and can capture any finite pattern that doesn’t have coin-flipping randomness built into it. While that might seem ideal, you’ve learned enough to know that there is a tradeoff. If we use unconstrained trees, we will likely overfit, and when we try to generalize, we’ll have poor test performance. If you need a reminder about that tradeoff, see Section 5.6. So, how can we bias our trees or place limits on them to prevent overfitting? We can take several steps.

1. We can limit the depth of the trees. We allow fewer questions before categorizing.

2. We can require more examples at leaves. This constraint forces us to group together examples that might be different. Since we aren’t allowed to separate them them, it effectively smoothes out some of our boundaries.

3. We can limit the number of features we consider when we ask questions of the examples. This constraint has the added benefit of speeding up our learning process.

8.3.1 Performing SVC

There are a few practical details that go along with using SVC:

• SVCs aren’t naturally suited to multiclass classification. They are typically wrapped up in either one-versus-one (OvO) or one-versus-rest (OvR) systems. We talked about these differences in Sections 6.3.4 and 6.4. Note, you don’t have to add this capability to SVMs. It is done behind the scenes for you. As of scikit-learn version 0.19, these methods are all standardized on using OvR. Prior to that, there was a mix of OvO and OvR.

• There are four ways (actually more) that we can get a SVC in sklearn: (1) using LinearSVC, (2) using SVC with a linear kernel, (3) using SVC with a polynomial kernel of degree 1 (a line in disguise), and (4) using a NuSVC with a linear kernel. These four methods don’t necessarily lead to the exact same results due to mathematical, implementation, and default-argument differences. Reconciling the differences is painful; I have some notes about it at the end of the chapter. Also, we haven’t discussed kernels yet and we’ll hold off on discussion them until Section 13.2.4. For now, consider them a coding detail—although they are far more than that.

8.3.1.1 Just the Facts: Running SVCs

Here, I’ll focus on just two of these SVC options: SVC and NuSVC. I’ll get into the nu parameter in just a moment, but I selected its value of .9 to get a result close to that of the SVC.

In [12]:

Click here to view code image

sv_classifiers = {"SVC(Linear)"   : svm.SVC(kernel='linear'),
                  "NuSVC(Linear)" : svm.NuSVC(kernel='linear', nu=.9)}

In [13]:

Click here to view code image

fig, axes = plt.subplots(1,2,figsize=(6,3))
for (name, mod), ax in zip(sv_classifiers.items(), axes.flat):
    plot_boundary(ax, iris.data, iris.target, mod, [0,1])
    ax.set_title(name)
plt.tight_layout()

To a quick glance, SVC and NuSVC are pretty similar, but the precise angles of the region boundaries are not identical.

8.3.1.2 Parameters for SVCs

SVC relies on one primary parameter, C, to control its bias-variance tradeoff. C can be difficult to interpret directly. NuSVC solves the same task as SVC, but it relies on different mathematics. We bother with it because the primary parameter for NuSVC,ν—pronounced like new and written in English as nu—has a simple meaning: at least ν % of the data will be kept as a support vector. It also has a consequence on errors, but errors of a special type: margin errors. Margin errors are points that are (1) either on the wrong side of the separator (a classification error) or (2) on the correct side of the separator (correctly classified) but within the margin. So, the other effect of ν is that we tolerate at most ν% margin errors in our training data. Under certain circumstances, margin errors increase to ν and support vectors decrease to ν . Values of ν are in the range [0, 1] which we interpret as a percent from 0% to 100%. While harder to interpret, SVC has better runtime characteristics than NuSVC.

The parameters for SVCs have a bit of occultness to them: they are hidden secrets known only to the alchemists. In truth, you have to dive deeply into some heavy mathematics to see what they mean. Still, we can explore their effects on some small examples. (I said small, not easy.) Let’s look at how varying C and ν affects the boundary between classes.

In [14]:

Click here to view code image

def do_linear_svc_separators(svc_maker, pname, params, ax):
    'create svc(params) and draw seperation boundary'
    xys = (np.linspace(2,8,100),
           np.linspace(2,8,100))

    for p in params:

        kwargs = {pname:p, 'kernel':'linear'}
        svc = svc_maker(**kwargs).fit(ftrs, tgt)
        # plot_separator is in mlwpy.py
        plot_separator(svc, *xys,
                       '{}={:g}'.format(pname, p), ax=ax)

In [15]:

Click here to view code image

ftrs = np.array([[3,3],
                 [3,6],
                 [7,3],
                 [7,6],
                 [6,3]])
tgt  = np.array([0,0,1,1,0])
colors = np.array(['r', 'b'])

Cs = [.1, 1.0, 10]
nus = [.3, .4, .5]

fig, axes = plt.subplots(1,3,figsize=(12,4),
                         sharex=True, sharey=True)
for ax in axes:
    ax.scatter(ftrs[:,0], ftrs[:,1], c=colors[tgt])
ax.set_xlim(2,8); ax.set_ylim(2,7)

do_linear_svc_separators(svm.SVC,   "C",   Cs, axes[1])
do_linear_svc_separators(svm.NuSVC, "nu", nus, axes[2])

axes[0].set_title("No Boundary")
axes[1].set_title("C Boundaries")
axes[2].set_title(r"$
u$ Boundaries");

# the two right most points are blue
# the remaining three points are red

There are two take-home messages here:

1. A bigger ν and a smaller C have approximately the same effect. The scales of ν and C are quite different, however. We’re using orders of magnitude in C and we’re using linear, one-tenth, steps in ν.

2. Bigger ν and smaller C can get us a SVC that to some extent ignores misclassification.

8.3.2 Bias and Variance in SVCs

One last set of comments is appropriate here. Let’s look at how our parameters—v in NuSVC and C in SVC—relate to bias and variance. We’ll start by creating some data:

In [16]:

Click here to view code image

ftrs, tgt = datasets.make_blobs(centers=2,
                                n_features=3,
                                n_samples=200,
                                center_box = [-2.0, 2.0],
                                random_state=1099)

# note: using three features, but graphing only two dimensions
fig, ax = plt.subplots(1,1,figsize=(4,3))
ax.scatter(ftrs[:, 0], ftrs[:, 1],
           marker='o', c=tgt, s=25, edgecolor='k')
ax.axis('off');

# generally the yellow class is on top
# and the purple class is on bottom

Now, we’ll look at the effect of v:

In [17]:

Click here to view code image

nus = np.linspace(0.05, 1.0, 10)
tt = skms.validation_curve(svm.NuSVC(kernel='linear'),
                           ftrs, tgt,
                           param_name='nu',
                           param_range=nus,
                           cv=5)

fig,ax = plt.subplots(1,1,figsize=(4,3))
ax = sns.tsplot(np.array(tt).transpose(),
                time=nus,
                condition=['Train', 'Test'],
                interpolate=False)

ax.set_title('5-fold CV Performance for NuSVC')
ax.set_xlabel("
".join([r'$
u$ for $
u$-SVC']))
ax.set_ylim(.3, 1.01)
ax.legend(loc='lower center');

Here we see that a very large ν is basically awful for training and testing. We can’t capture enough of the pattern to do anything—we are too biased. On the other end, decreasing v lets us capture some pattern—but when we go to test, we simply don’t do very well. We aren’t generalizing because we have overfit the training data. Broadly speaking, a small ν is equivalent to a large C, although the scales differ.

In [18]:

Click here to view code image

cs = [0.0001, 0.001, 0.01, .1, 1.0, 10, 100, 1000]
tt = skms.validation_curve(svm.SVC(kernel='linear'),
                           ftrs, tgt,
                           param_name='C',
                           param_range=cs,
                           cv=5)

fig,ax = plt.subplots(1,1,figsize=(4,3))
ax = sns.tsplot(np.array(tt).transpose(),
                time=cs,
                condition=['Train', 'Test'],
                interpolate=False)

ax.set_title('5-fold CV Performance for SVC')
ax.set_xlabel("
".join([r'C for SVC']))
ax.set_ylim(.8, 1.01)
ax.set_xlim(.00001, 10001)
ax.set_xscale('log')

On the left, at small C values, both our training and testing performance is relatively poor. On the right, at large C, our training performance is better than our test. Putting these together, high values of C lead to overfitting and low values of C lead to underfitting. While C is harder to interpret than ν, it trades off between the complexity of our model and the errors we make. A bigger C means that we care more about errors compared to complexity. With a really big C, even the smallest errors matter a lot. So, we build a model with a lot of complexity to cover those errors. We’ll make our view of this tradeoff more concrete in Chapter 15.

8.4.1 Betting Odds

My friends that like to bet—on basement poker, at the casino, or on the ponies at the racetrack—are very familiar with thinking in terms of odds. I . . . am not. So, let’s spend a couple of minutes talking about probabilities and odds. Here’s a very simple example of the relationship between probabilities and odds. Imagine our probability—we’ll say of winning—is 10%. That means if we play a game ten times, we expect to win once. We can break that down another way: of ten total attempts we expect one win and nine losses. If we create the ratio of those two numbers, we get 19 ≈ .1111. These are the odds of winning. We’ll also write those odds as 1 : 9. Be very careful: even though this is the odds and we calculate it from a ratio, this value is not the odds-ratio—that is a different concept.

Back to odds: how can we interpret them? Why do my betting friends like to think in terms of odds? To answer that, let’s ask another question. For a given set of odds, what is a fair bet for those odds? Specifically, if the odds of winning are .1111, what amount of money do the participants need to wager so that, in the long run, the game is fair. To keep this from getting too abstract, let’s design a game that matches the 10% probability—or 19 odds—of winning.

We’ll start by taking nine spades and one heart from a deck of cards. I’ll sit down with my friend, Andy. We’ll shuffle the cards and then my friend deals me one card. If it is the heart, I win! If not, Andy wins. This setup gives us a game with a 10% probability, or 1 : 9 odds, of MarkWins—go, me! How much money should Andy and I be willing to risk on this simple game if we want to have a fair outcome? In the long run, what is the break-even point where we both expect to win the same amount of money? Note that we talk about playing the game many times to reduce the effect of chance variability. If we only play one round, only one person will win that round—probably Andy! If we play 100 times, we expect to see something closer to a 90–10 split for Andy winning. There is no guarantee, though.

To figure out the break-even point, let’s start with some concrete numbers. Here’s an example where we both wager $10.

To compute the winnings, we took the two possible outcomes—a win and a loss—and combined (1) the two probabilities of those outcomes and (2) the two monetary results of those outcomes together with a—tada!—dot product. Writing that out mathematically gives us ∑_outcome P_outcome υ_outcome, where p and υ are the probabilities and the dollar-values for each outcome. This particular dot product is called the expected value of winnings when someone plays the game.

Notice that since no money disappears, we have a true zero-sum game and our total winnings must balance out to zero. So, if we both risk an equal amount of money—$10 for each of us—I, Mark, am really going to be in the hole. Let’s sanity-check that result—do the numbers make sense? Remember, my odds of winning were only 1:9. Sadly, I don’t have a very good chance of winning. To balance things out, I should stake less money than Andy because I have lower odds of winning. What is the break-even point for a bet? We could perform some algebra to calculate the answer, but let’s do it experimentally with some code. We’ll look at pairs of bets from $1 to $11 in steps of $2 and compute Mark’s winnings.

We’ll make use of two helper functions:

In [19]:

Click here to view code image

def simple_argmax(arr):
    ' helper to convert np.argmax into something usable '
    return np.array(np.unravel_index(np.argmax(arr),
                                     arr.shape))

def df_names(df, idxs):
    ' helper to convert number of index/column labels '
    r,c = idxs
    return df.index[r], df.columns[c]

Then, we’ll create a table of the outcomes for several combinations of betting:

In [20]:

Click here to view code image

base_bets = np.arange(1,12,2)
mark_bet, andy_bet = np.meshgrid(base_bets, base_bets)

mark_winnings = .1 * andy_bet + .9 * -mark_bet

df = pd.DataFrame(mark_winnings,
                  index  =base_bets,
                  columns=base_bets)
df.index.name = "Andy Bet"
df.columns.name = "Mark Bet"

print("Best Betting Scenario (for Mark) for These Values:")
print("(Andy, Mark):", df_names(df, simple_argmax(mark_winnings)))

display(df)

Click here to view code image

Best Betting Scenario (for Mark) for These Values:
(Andy, Mark): (11, 1)

That’s pretty interesting. Recall from our discussion above: if my overall expected winnings are zero, so are Andy’s. The best outcome for me, not surprisingly, is in the lower-left corner of that table. It occurs when I wager $1 and Andy wagers $11. That’s my lowest bet and Andy’s highest bet. Now, if Andy is willing to play a game where I bet $1 and he bets $99, things are looking very different for me. I win 10% of the time, so I’m looking at .1 × $99 + .9 × − $1 = 9. If we played this game with these bets many times, I’d start coming out ahead. Things are looking up for ol’ Marco.

What about the break-even point? That’s where the winnings for both of us are the same, $0.00. It’s close to the bottom-left corner: I wager $1 and Andy wagers $9. Compare that to my odds of winning: 1 : 9. The break-even point is the bet where the amount of money you stake is equal to your odds of winning. Andy is a 9 : 1 favorite: he bets $9 for every $1 Mark bets. I am a 1 : 9 long-shot. I’ll only bet $1 for every $9 that Andy bets.

Here’s one last take-home message from betting. If two players had an equal probability of winning, the probabilities would be .5 each. These correspond to an odds of 1 : 1 which we write as odds = 1. These values are the tipping point between winning and losing. Higher values (.75, odds 3 : 1) make one event or winner more likely and the other less likely.

8.4.2 Probabilities, Odds, and Log-Odds

Hopefully, you now have some understanding of how odds work. Earlier, I mentioned that we care about the log-odds. I’ll explain why in a minute. Let’s start by creating a table of some probability values with their corresponding odds and log-odds. The log-odds are literally just that: the mathematical logarithm applied to the odds values: log(odds).

In [21]:

Click here to view code image

tail_probs = [0.0, .001, .01, .05, .10, .25, 1.0/3.0]

lwr_probs = np.array(tail_probs)
upr_probs = 1-lwr_probs[::-1]
cent_prob = np.array([.5])

probs = np.concatenate([lwr_probs, cent_prob, upr_probs])

# much better than geterr/seterr/seterr
with np.errstate(divide='ignore'):
    odds     = probs / (1-probs)
    log_odds = np.log(odds)

index=["{:4.1f}%".format(p) for p in np.round(probs,3)*100]

polo_dict = co.OrderedDict([("Prob(E)",       probs),
                            ("Odds(E:not E)", odds),
                            ("Log-Odds",      log_odds)])
polo_df = pd.DataFrame(polo_dict, index=index)
polo_df.index.name="Pct(%)"
polo_df

Out[21]:

If you prefer a graphical view, let’s look at the relationship between probabilities and odds (expressed as fractions):

In [22]:

Click here to view code image

def helper(ax,x,y,x_name,y_name):
    ax.plot(x,y, 'r--o')
    ax.set_xlabel(x_name)
    ax.set_ylabel(y_name)

# note, we trim the values above 90% [index -5] b/c
# the scale of the plots gets too compressed
# (huh, log-scale takes care of that! funny .....)
fig, (ax0, ax1) = plt.subplots(1,2, figsize=(9,3))
helper(ax0, probs[:-5], odds[:-5], 'probability', 'odds')
helper(ax1, odds[:-5], probs[:-5], 'odds', 'probability')

and the relationship between probabilities and log-odds:

In [23]:

Click here to view code image

fig, (ax0, ax1) = plt.subplots(1,2, figsize=(9,3))
helper(ax0, probs, log_odds, 'probability', 'log-odds')
helper(ax1, log_odds, probs, 'log-odds', 'probability')

If you look at the first and last rows of the table, you can see the extreme values for each of the probabilities, odds, and log-odds. The min and max probabilities correspond with events that are either impossibilites or guarantees. Of course, we know there are rarely such things. (You can now meditate on the impossibility of impossibilities and then come back to your happy place.)

Here are the ranges of values:

In [24]:

Click here to view code image

pd.DataFrame([polo_df.min(axis=0),
              polo_df.max(axis=0)], index=['min', 'max']).T

Out[24]:

There are a few important points here. The ranges of our values go from [0, 1] to (0,∞) to (−∞,∞) as we move from probabilities to odds to log-odds. Now, I’m ready to drop a bombshell on you. If we predict the log-odds from our input features, logistic regression and linear regression are basically doing the same thing! I do have a weasel word, basically, in there because there are a few caveats.

You might recall from Section 4.3.3 our calculation for the predicted linear regression value: predicted_value=rdot(w, x). For logistic regression, the equivalent calculation is predicted_log_odds = rdot(w, x). And now you know why logistic regression has regression in its name. The mathese way to write this is LO=Σftrswfxf. Actually, stats LO^ with a hat for predicted or estimated values. But I’m going to leave that out.

In linear regression, we are predicting a target output value that can range anywhere from a large-magnitude negative value (–1,000,000 or less) to a large-magnitude positive value (+1,000,000 or more). Probabilities don’t do that—they go from zero to one. Odds don’t do that—they go from zero to large, positive values. But log-odds? Yes, they can do that! Log-odds are a version of probabilities that go from very small negative values to very large positive values. Log-odds are just the type of value that linear regression needs for a well-behaved target. We can leverage that for our devious logistic regression purposes.

Of course, we aren’t usually satisfied by getting the log-odds. For classification problems, we want to predict the outcome class: {cat, dog} or {False, True}. So, we need a little more machinery. Let me write out the longer form of two mathematical abbreviations we are going to use. We’re going to simplify things a bit and assume we are dealing with a binary classification problem—there are only two classes, so if something is not-a-cat it must be dog. We care about (1) the probability that an example belongs to a target class and (2) the log-odds that an example belong to a target class. We can write these as:

• The probability of targethood for an example x: P(x is-a tgt) = P_tgt(x).

• The log-odds of targethood for an example x: LO(x is-a tgt) = LO_tgt(x).

Think about each x that follows as an example. We can get away with focusing on a single target, since if something is not that target, then it must be the other class. We’ll drop the tgt subscript and we’re left with P(x) and LO(x). Based on our discussion of betting and our table of equivalent values, we know that we’ll lean towards our chosen target when P(x) > .5 or LO(x) > 0.

The second equality comes from the definition of the log-odds: it’s the log of the odds and the odds are the inner fraction on that right-hand side. The logit is simply a name given to converting probabilities to log-odds. A probability, like P(x), goes in and its log-odds, LO(x), comes out. Since I love arrows, the logit takes P(x)→logP(x)1−P(x)=LO(x). We actually used code for this above when we created the table of probabilities, odds, and log-odds. I’m sneaky like that. Here’s what it looks like as a stand-alone function:

In [25]:

Click here to view code image

def logit(probs):
    odds = probs / (1-probs)
    log_odds = np.log(odds)
    return log_odds

We can also solve for P(x) and see what happens. Note that exp and log are opposites of each other: one undoes the other. It’s a little clunky to write out exp, the exponential function, like this, but it prevents confusion from too many superscripts.

The logistic function is a special name for taking LO(x)→exp(LO(x))1+exp(LO(x)=P(x). So now we have two functions that work in opposite directions:

• logit(P(x)) takes us from a probability to the log-odds

• logistic(LO(x)) takes us from log-odds to a probability

Why do we care? Because we have to make a decision. If the log-odds are greater than 0, LO(x) > 0, then the odds favor tgt. That means we’re in the case when the odds are greater than one and the probability is greater than 50%. If the log-odds are less than 0, LO(x) < 0, the odds favor the other of the two targets, not-tgt or ¬ tgt. That means that when LO(x) = 0, we are at the boundary between the two. That boundary is precisely

When that left-hand sum—a dot product—is zero, we are essentially at a loss to pick between tgt and ¬ tgt.

8.4.3 Just Do It: Logistic Regression Edition

sklearn has several methods for performing logistic regression. We call them through LogisticRegression and SGDClassifier. In Section 4.4, we talked about four ways of picking a “preferred” set of parameters. The methods used by sklearn for logistic regression are smart step methods: from a starting point, make some adjustments, and repeat as necessary until the answer is good enough. SGD stands for Stochastic Gradient Descent and it is one way of performing smart steps. It makes its adjustments by looking at the errors in the current guess and using those to lower the error of the next guess. We tell SGDClassifier to use a log-loss model of the errors which gives us logistic-regression-like behavior. Other losses lead to other classification methods which we’ll see in Chapter 15. SGDClassifier can handle very large problems, but it takes multiple iterations to do so and, because of its internal use of randomness, every run may result in a different answer. With enough data and small enough error tolerance, SGDClassifier should reach, or converge to, similar answers on different runs.

The other logistic regression method we’ll use is LogisticRegression with method='saga'. I’ll save futher discussion of saga for the end notes—but briefly, saga allows us to use a full multiclass model instead of wrapping a binary classification with a one-versus-rest.

In [26]:

Click here to view code image

# Both options come with "regularization" turned ON
# we'll ignore that for now, but see Chapter 9 for more details
LogReg = linear_model.LogisticRegression
SGD    = linear_model.SGDClassifier
logreg_classifiers = {'LogReg(saga)': LogReg(solver='saga',
                                             multi_class='multinomial',
                                             max_iter=1000),
                      'LogReg(SGD)' : SGD(loss='log', max_iter=1000)}

fig, axes = plt.subplots(1,2,figsize=(12,4))
axes = axes.flat
for (name, mod), ax in zip(logreg_classifiers.items(), axes):
    plot_boundary(ax, iris.data, iris.target, mod, [0,1])
    ax.set_title(name)
plt.tight_layout()

8.4.4 A Logistic Regression: A Space Oddity

Here’s an oddity of logistic regression: if all the data falls nicely into two clusters, then there is an infinite number of lines we can draw between the clusters. Logistic regression doesn’t have a built-in answer to picking one of these infinite alternatives. Trying to solve a perfectly separable classification problem with logistic regression may lead to problematic answers. Fortunately, (1) those problems are more serious for statisticians than they are for us using logistic regression as a black-box prediction method and (2) for practical purposes in interesting problems, we will never have perfectly separable data. Still, here’s an example of the issue.

In [27]:

Click here to view code image

fig, ax = plt.subplots(1,1,figsize=(4, 1))

x = np.array([1,2,5,10]).reshape(-1, 1)
y = ['red', 'blue', 'red', 'blue']
ax.scatter(x,np.zeros_like(x), c=y);

This is a typical scenario: the two classes are intertwined. We’ll use a non-sklearn method to perform logistic regression. This method is a bit old-school, but it will expose our issue clearly.

In [28]:

Click here to view code image

import statsmodels.formula.api as sm

x = np.c_[x, np.ones_like(x)] # +1 trick
tgt = (np.array(y) == 'red')

# sm.Logit is statsmodels name for logistic regression
(sm.Logit(tgt, x, method='newton')
   .fit()
   .predict(x))  # training predictions

Optimization terminated successfully.
         Current function value: 0.595215
         Iterations 5

Out[28]:

Click here to view code image

array([0.7183, 0.6583, 0.4537, 0.1697])

Everything seems pretty well behaved, so far. Now, look what happens with a seemingly minor change to the data.

In [29]:

Click here to view code image

fig, ax = plt.subplots(1,1,figsize=(4,1))

x = np.array([1,4,6,10]).reshape(-1, 1)
y = ['red', 'red', 'blue', 'blue']
ax.scatter(x, np.zeros_like(x), c=y);

In [30]:

Click here to view code image

x = np.c_[x, np.ones_like(x)] # +1 trick
tgt = (np.array(y) == 'red')
try:
    sm.Logit(tgt, x, method='newton').fit().predict(x) # in-sample predictions
except Exception as e:
    print(e)

Click here to view code image

Perfect separation detected, results not available

Surprisingly, Logit refuses to solve the problem for us. It warns us that there was perfect separation between the classes and there are no results to use. It seems like drawing the perfect line would be easy. It isn’t. The problem is that there is an infinite number of lines that we could draw and our old-school logistic regression doesn’t have a built-in way to pick between them. In turn, some methods don’t do well with that uncertainty and can give very bad answers. Hence, Logit stops with a fail.

8.5.1 Covariance

To understand the differences between the DA methods, you need to know about covariance. Covariance describes one way in which the features are related—or not—to each other. For example, if we are looking at physiological data on medical patients, our models might make good use of the fact that height and weight have a strong relationship. The covariance encodes the different ways features may metaphorically communicate with each other.

A quick point: in this section and this chapter, we are talking about the use of covariance as an internal widget of a learning machine. Different constraints on covariance lead to different learning machines. On the other hand, you might be familiar with the difficulties some models have when features are too closely related. We are not addressing those issues here; we’ll talk about it when we discuss feature selection in Section 13.1.

We’ll start our discussion by talking about variance. If you remember our discussions in Chapter 2, you’ll recall that the variance is the sum of squared errors of a model that predicts the mean value. You might even be able to come up with an equation for that. Before you scramble for pencil and paper, for a feature X that formula looks like:

Remember that X¯=1nΣx is the mean of the set of data X. This formula is what I will call the common formula for variance. (Footnote: I’m ignoring the difference between variance of a random variable, variance of a population, and variance of a finite sample. If you are uneasy, take a deep breath and check out the End-of-Chapter Notes.) You might recognize a dot product in the formula for variance: var_X = dot(x-mean_X, x-mean_X) / n. If we write the variance out as code for the sum of squared errors from the mean, it might be even more familiar.

In [31]:

Click here to view code image

X = np.array([1,3,5,10,20])
n = len(X)

mean_X = sum(X) / n
errors = X - mean_X
var_X = np.dot(errors, errors) / n

fmt = "long way: {}nbuilt in: {}
 close: {}"
print(fmt.format(var_X,
                 np.var(X),
                 np.allclose(var_X, np.var(X)))) # phew

long way: 46.16
built in: 46.16
   close: True

8.5.1.1 The Classic Approach

Now, if we have two variables, we don’t get quite the same easy verbal phrasing of comparing with a mean model. Still, if I said that we take two models that predict the means for the two variables and multiply them together, you might come up with something like:

Cov(X,Y)=1nΣx∈Xy∈Y(x−X¯)(y−Y¯)

I apologize for using X and Y as two potential features. I’d use subscripts, but they are easily lost in the shuffle. I’m only going to do that in this section. In code, that turns into:

In [32]:

Click here to view code image

X = np.array([1,3,5,10,20])
Y = np.array([2,4,1,-2,12])

mean_X = sum(X) / n
mean_Y = sum(Y) / n

errors_X = X - mean_X
errors_Y = Y - mean_Y

cov_XY = np.dot(errors_X, errors_Y) / n
print("long way: {:5.2f}".format(cov_XY))
print("built in:", np.cov(X,Y,bias=True)[0,1])
# note:
# np.cov(X,Y,bias=True) gives [Cov(X,X), Cov(X,Y)
#                              Cov(Y,X), Cov(Y,Y)]

long way: 21.28
built in: 21.28

Now, what happens if we ask about the covariance of a feature with itself? That means we can set Y = X, filling in X for Y, and we get:

Cov(X,X)=1nΣx∈X(x−X¯)(x−X¯)=1nΣx∈X(x−X¯)2=Var(X)

That’s all well and good, but we’ve gotten pretty far off the track of giving you some intuition about what happens here. Since the variance is a sum of squares, we know it is a sum of positive values because squaring individual positive or negative numbers always results in positives. Adding many positive numbers also gives us a positive number. So, the variance is always positive (strictly speaking, it can also be zero). The covariance is a bit different. The individual terms in the covariance sum will be positive if both x and y are greater than their means or if both x and y are less than their means (Figure 8.6). If they are on different sides of their means (say, x>X¯ and y<Y¯), the sign of that term will be negative. Overall, we could have a bunch of negative terms or a bunch of positive terms or a mix of the two. The overall covariance could be positive or negative, close to zero or far away.

var_x = 0
n = len(X)
for i in range(n):
    for j in range(i, n): # rest of Xs
        var_x += (X[i] - X[j])**2
print("Var(X):", var_x / n**2)

Var(X): 46.16

cov_xy = 0
for i in range(len(X)):
    for j in range(i, len(X)): # rest of Xs, Ys
        cov_xy += (X[i] - X[j])*(Y[i]-Y[j])
print("Cov(X,Y):", cov_xy / n**2)

Cov(X,Y): 21.28

cov_XY = 0.0
xy_pairs = it.product(zip(X,Y), repeat=2)
for (x_i, y_i), (x_j, y_j) in xy_pairs:
    cov_XY += (x_i - x_j) * (y_i - y_j)
print("Cov(X,Y):", cov_XY / (2 * n**2))

Cov(X,Y): 21.28

cov_XX = 0.0
for x_i, x_j in it.combinations(X, 2):
    cov_XX += (x_i - x_j)**2
print("Cov(X,X) == Var(X):", cov_XX / (n**2))

Cov(X,X) == Var(X): 46.16

cov_XY = 0.0
for (x_i, y_i), (x_j,y_j) in it.combinations(zip(X,Y), 2):
    cov_XY += (x_i - x_j) * (y_i - y_j)
print("Cov(X,Y):", cov_XY / (n**2))

Cov(X,Y): 21.28

8.5.1.3 Visualizing Covariance

Let’s visualize what is going on with these rectangle areas and covariances. If we can think of covariance as areas of rectangles, let’s draw these rectangles. We’ll use a simple example with three data points and two features. We’ll draw the diagonal of each of the three rectangles and we’ll color in the total contributions at each region of the grid. Red indicates a positive overall covariance; blue indicates a negative covariance. Darker colors indicate more covariance in either the positive or negative direction: lighter colors, leading to white, indicate a lack of covariance. Our technique to get the coloring right is to (1) build a NumPy array with the proper values and (2) use matplotlib’s matshow, matrix show, to display that matrix.

We have a few helpers for “drawing” the rectangles. I use scare-quotes because we are really filling in values in an array. Later, we’ll use that array for the actual drawing.

In [38]:

Click here to view code image

# color coding
# -inf -> 0; 0 -> .5; inf -> 1
# slowly at the tails; quickly in the middle (near 0)
def sigmoid(x):
    return np.exp(-np.logaddexp(0, -x))

# to get the colors we need, we have to build a raw array
# with the correct values; we are really "drawing"
# inside a numpy array, not on the screen
def draw_rectangle(arr, pt1, pt2):
    (x1,y1),(x2,y2) = pt1,pt2
    delta_x, delta_y = x2-x1, y2-y1
    r,c = min(y1,y2), min(x1,x2) # x,y -> r,c
    # assign +/- 1 to each block in the rectangle.
    # total summation value equals area of rectangle (signed for up/down)
    arr[r:r+abs(delta_y),
        c:c+abs(delta_x)] += np.sign(delta_x * delta_y)

Now, we’ll create our three data points and “draw”—fill in the array—the three rectangles that the points define:

In [39]:

Click here to view code image

# our data points:
pts = [(1,1), (3,6), (6,3)]
pt_array = np.array(pts, dtype=np.float64)

# the array we are "drawing" on:
draw_arr = np.zeros((10,10))
ct = len(pts)
c_magic = 1 / ct**2 # without double counting

# we use the clever don't-double-count method
for pt1, pt2 in it.combinations(pts, 2):
    draw_rectangle(draw_arr, pt1, pt2)
draw_arr *= c_magic

In [40]:

Click here to view code image

# display the array we drew
from matplotlib import cm
fig, ax = plt.subplots(1,1,figsize=(4,3))
ax.matshow(sigmoid(draw_arr), origin='lower', cmap=cm.bwr, vmin=0, vmax=1)
fig.tight_layout()

# show a diagonal across each rectangles
# the array elements are centered in each grid square
ax.plot([ .5, 2.5],[ .5, 5.5], 'r') # from 1,1 to 3,6
ax.plot([ .5, 5.5],[ .5, 2.5], 'r') # from 1,1 to 6,3
ax.plot([2.5, 5.5],[5.5, 2.5], 'b'); # from 3,6 to 6,3

That graphic represents three datapoints defined by two features each.

In [41]:

Click here to view code image

np_cov = np.cov(pt_array[:,0], pt_array[:,1], bias=True)[0,1]
print("Cov(x,y) -   from numpy: {:4.2f}".format(np_cov))

# show the covariance, as calculated from our drawing
print("Cov(x,y) - our long way: {:4.2f}"}.format(draw_arr.sum()))

Click here to view code image

Cov(x,y) -   from numpy: 1.22
Cov(x,y) - our long way: 1.22

In the diagram, red indicates a positive relationship between two data points: as x goes up, y goes up. Note that if I flip the points and draw the line backwards, this is the same as saying as x goes down, y goes down. In either case, the sign of the terms is the same. Reds contribute to a positive covariance. On the other hand, blues indicate an opposing relationship between x and y: x up, y down or x down, y up. Finally, the intensity of the color indicates the strength of the positive or negative relationship for the two points that define that rectangle. The total covariance for the pair of points is divided equally among the squares of the rectangle. To get the final color, we add up all the contributions we’ve gotten along the way. Dark red is a big positive contribution, light blue is a small negative contribution, and pure white is a zero contribution. Finally, we divide by the number of points squared.

Here’s what the raw numbers look like. The value in a grid square is precisely what controls the color in that grid square.

In [42]:

Click here to view code image

plt.figure(figsize=(4.5,4.5))
hm = sns.heatmap(draw_arr, center=0,
                 square=True, annot=True,
                 cmap='bwr', fmt=".1f")
hm.invert_yaxis()
hm.tick_params(bottom=False, left=False)

Our discussion has been limited to the covariance between two features: X and Y . In our datasets, we might have many features—X, Y, Z, . . .—so we can have covariances between all pairs of features: Cov(X, Y), Cov(X, Z), Cov(Y, Z), and so on. Here’s an important point: the covariance formula for two features we used above relied on calculations between pairs of data points {(x₁, y₁), (x₂, y₂)} for those two features. When we talk about all the covariances, we are talking about the relationships between all pairs of features and we need to record them in a table of some sort. That table is called a covariance matrix. Don’t be scared. It is simply a table listing the covariances—the average sums of rectangle areas—between different pairs of variables. The covariance between X and Y is the same as the covariance between Y and X, so the table is going to have repeated entries.

Here’s an example that has relatively little structure in the data. What do I mean by structure? When we look at the covariance matrix, there aren’t too many patterns in it. But there is one. I’ll let you find it.

In [43]:

Click here to view code image

data = pd.DataFrame({'X':[ 1, 3, 6],
                     'Y':[ 1, 6, 3],
                     'Z':[10, 5, 1]})
data.index.name = 'examples'

# it's not critical to these examples, but Pandas' cov is
# "unbiased" and we've been working with "biased" covariance
# see EOC notes for details
display(data)
print("Covariance:")
display(data.cov())

	X	Y	Z
examples
0	1	1	10
1	3	6	5
2	6	3	1

Covariance:

	X	Y	Z
X	6.3333	1.8333	-11.1667
Y	1.8333	6.3333	-5.1667
Z	-11.1667	-5.1667	20.3333

I’ll talk about the values in that matrix with respect to the main diagonal—the 6.3, 6.3, and 20.3 values. (Yes, there are two diagonals. The “main” diagonal we care about is the one running from top-left to bottom-right.)

You may have noticed two things. First, the elements are mirrored across the main diagonal. For example, the top-right and bottom-left values are the same (–11.1667). That is not a coincidence; all covariance matrices are symmetric because, as I pointed out above, Cov(X, Y) = Cov(Y, X) for all pairs of features. Second, you may have picked up on the fact that both X and Y have the same variance. It shows up here as Cov(X, X) and Cov(Y, Y).

Now, imagine that our different features are not directionally related to each other. There’s no set pattern: as one goes up, the other can either go up or down. We might be trying to relate three measurements that we really don’t expect to be related at all: height, SAT scores, and love of abstract art. We get something like this:

In [44]:

Click here to view code image

data = pd.DataFrame({'x':[ 3, 6, 3, 4],
                     'y':[ 9, 6, 3, 0],
                     'z':[ 1, 4, 7, 0]})
data.index.name = 'examples'
display(data)
print("Covariance:")
display(data.cov()) # biased covariance, see EOC

	x	y	z
examples
0	3	9	1
1	6	6	4
2	3	3	7
3	4	0	0

Covariance:

	x	y	z
x	2.0000	0.0000	0.0000
y	0.0000	15.0000	0.0000
z	0.0000	0.0000	10.0000

The data numbers don’t look so special, but that’s a weird covariance matrix. What’s going on here? Let’s plot the data values:

In [45]:

Click here to view code image

fig, ax = plt.subplots(1,1,figsize=(4,3))
data.plot(ax=ax)
ax.vlines([0,1,2,3], 0, 10, colors=".5")

ax.legend(loc='lower center', ncol=3)

plt.box(False)
ax.set_xticks([0,1,2,3])
ax.set_ylabel("values");

We see that we never get a consistent pattern. It is not as simple as “if X goes up, Y goes up.” We also don’t see any consistency between X and Z or Y and Z—there’s no simple pattern of “you go up, I go down.” There’s always some segment where it goes the other way. For example, blue and green go up together in segment one, but work against each other in segments two and three. I constructed the data so that not only are the covariances low, they cancel out more or less exactly: all of the off-diagonal covariances in the matrix are zero. The only non-zero entries are on the diagonal of the table. We call this a diagonal covariance matrix. X, Y, and Z all have their own variance, but they have no pairwise covariance. If their own variances were zero, that would mean that the sum of rectangle sizes was zero. That only happens if all the values are the same. For example, with x₁ = x₂ = x₃ = 42.314, the not-quite-a-rectangle we construct from these xs would be a single point with no length or width.

All of this discussion has been about one covariance matrix. In a few minutes, we’ll take about how that matrix influences our DA methods. But we can’t always rely on one matrix to carry all of the information we need. If we have multiple classes, you can imagine two scenarios: one where there is a single covariance matrix that is the same for every class—that is, one covariance is enough to describe everything. The second case is where we need a different covariance matrix for each class. We’ll ignore middle grounds and either have one matrix overall or have one for each class.

Let’s summarize what we’ve learned about the covariance. In one interpretation, the covariance simply averages the sizes of pairwise rectangles constructed from two features. Bigger rectangles mean bigger values. If the rectangle is built by moving up-and-right, its value is positive. If a pair of features moves essentially independently of each other—any coordinated increase is always offset by a corresponding decrease—their covariance is zero.

8.5.2 The Methods

Now, we are equipped to talk about the differences between the four variations of discriminant analysis (DA): QDA, LDA, GNB, and DLDA. Q stands for quadratic, L stands for linear, DL stands for diagonal linear, and GNB is our old friend Gaussian Naive Bayes . . . that’s Naive Bayes on smoothly valued features. These techniques make different assumptions about the covariances—the average rectangle sizes we dove into above.

1. QDA assumes that the covariances between different features are unconstrained. There can be class-wise differences between the covariance matrices.

2. LDA adds a constraint. It says that the covariances between features are all the same regardless of the target classes. To put it another way, LDA assumes that regardless of target class, the same covariance matrix does a good job describing the data. The entries in that single matrix are unconstrained.

3. GNB assumes something slightly different: it says that the covariances between distinct features—for example, Feature One and Feature Two—are all zero. The covariance matrices have entries on their main diagonal and zeros everywhere else. As a technical note, GNB really assumes that pairs of features are independent within that class—which implies, or leads to, a Feature One versus Feature Two covariance of zero. There may be different matrices for each different target class.

4. DLDA combines LDA and GNB: the covariances are assumed to be the same for each class—there’s only one covariance matrix—and Cov(X, Y) is zero between pairs of nonidentical features (X ≠ Y).

I really emphasized the role of the assumptions in this process. Hopefully, it is clear: it is an assumption of the method, not necessarily the state of the world that produced the data. Do you have that all straight? No? That’s OK. Here’s a faster run through of the assumptions:

1. QDA: possibly different covariance matrices per class,

2. LDA: same covariance matrix for all classes,

3. GNB: different diagonal covariance matrices per class, and

4. DLDA: same diagonal covariance matrix for all classes.

Let’s make the idea of classwise covariance matrices and different covariance matrices per class concrete. Suppose I have a simple table of data with measurements on cats and dogs. The target class is whether we have a cat or dog. The features are length and weight. You can probably come up with two different ways to calculate the variance of the weights: either calculate the variance over all of the pets at once or calculate the variance over the cats and dogs separately so we keep track of two values. Calculating over all is similar to what we do with covariance in LDA and DLDA. Calculating separately per cats and dogs is what we do with covariance QDA and GNB. That is, in LDA and DLDA we would calculate the covariance of length and weight over cats and dogs together; in QDA and GNB, we would calculate the covariances separately for each pet type.

Here’s a summary Table 8.1, with some mathese for those that are so inclined.

8.5.3 Performing DA

So, let’s look at the operation of the DA methods. We’ll do a simple train-test split and look at the confusion matrices from each of the four methods.

In [46]:

Click here to view code image

qda  = discriminant_analysis.QuadraticDiscriminantAnalysis()
lda  = discriminant_analysis.LinearDiscriminantAnalysis()
nb   = naive_bayes.GaussianNB()
dlda = DLDA() # from mlwpy.py

da_methods = [qda, lda, nb, dlda]
names = ["QDA", "LDA", "NB", "DLDA"]

fig, axes = plt.subplots(2,2, figsize=(4.5, 4.5),
                         sharex=True, sharey = True)
for ax, model, name in zip(axes.flat, da_methods, names):
    preds = (model.fit(iris_train_ftrs, iris_train_tgt)
                  .predict(iris_test_ftrs))
    cm = metrics.confusion_matrix(iris_test_tgt, preds)
    sns.heatmap(cm, annot=True, cbar=False, ax=ax)
    ax.set_title(name)

axes[0,0].set_ylabel('Actual')
axes[1,0].set_xlabel('Predicted');

We should be wary of reading too much into the differences here because they are not substantial. However, there seems to be something to LDA as a sweet spot of the assumptions—based on Occam’s razor, we make the fewest assumptions that get the job done. There’s a bit of variation in the results when you rerun with multiple train-test splits, so I would never recommend hard-selling the success of LDA here. However, in a larger problem, it would be worthwhile to explore it in more detail. Let’s look at the borders these methods create.

In [47]:

Click here to view code image

fig, axes = plt.subplots(2,2,figsize=(4.5, 4.5))
axes = axes.flat

for model, ax, name in zip(da_methods, axes, names):
    # plot boundary only uses the specified (two) dimensions to predict
    plot_boundary(ax, iris.data, iris.target, model, [0,1])
    ax.set_title(name)
plt.tight_layout()

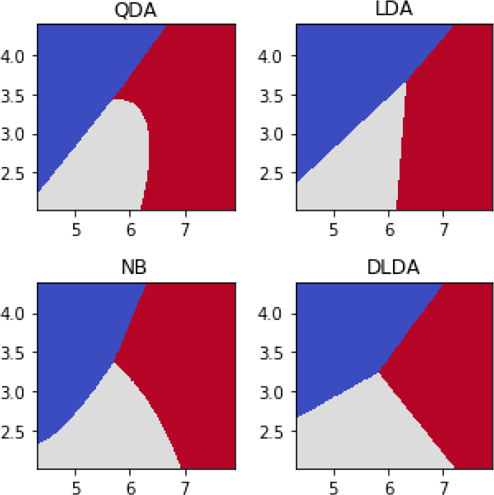
Both QDA and GNB have nonlinear boundaries—they curve a bit. LDA and DLDA both have linear borders between the classes.

8.7.1 Digits

Here we’re going to make use of the digits dataset that ships with sklearn.

In [49]:

Click here to view code image

digits = datasets.load_digits()

The data represents simple images of handwritten digits. For example, the first digit is

In [50]:

Click here to view code image

print("Shape:", digits.images[0].shape)
plt.figure(figsize=(3,3))
plt.imshow(digits.images[0], cmap='gray');

Shape: (8, 8)

and it has a target value of

In [51]:

digits.target[0]

Out[51]:

0

The dataset comes in two forms. One (digits.images) is appropriate for display purposes; I used it just above. The other (digits.data) is appropriate for use in learning. That form is a flattened row of the information in the square 64 × 64 images.

Now we can construct our learning problem.

In [52]:

Click here to view code image

classifier_parade = 
    {'LogReg(1)' : linear_model.LogisticRegression(max_iter=1000),
     'LogReg(2)' : linear_model.SGDClassifier(loss='log',
                                              max_iter=1000),

     'QDA' : discriminant_analysis.QuadraticDiscriminantAnalysis(),
     'LDA' : discriminant_analysis.LinearDiscriminantAnalysis(),
     'GNB' : naive_bayes.GaussianNB(),

     'SVC(1)' : svm.SVC(kernel="linear"),
     'SVC(2)' : svm.LinearSVC(),

     'DTC' : tree.DecisionTreeClassifier(),
     '5NN-C' : neighbors.KNeighborsClassifier(),
     '10NN-C' : neighbors.KNeighborsClassifier(n_neighbors=10)}
baseline = dummy.DummyClassifier(strategy="uniform")

base_score = skms.cross_val_score(baseline,
                                  digits.data, digits.target==1,
                                  cv=10,
                                  scoring='average_precision',
                                  n_jobs=-1)

We evaluate our solutions with cross-validation on the digits dataset.

In [53]:

Click here to view code image

fig, ax = plt.subplots(figsize=(6,4))
ax.plot(base_score, label='base')
for name, model in classifier_parade.items():
    cv_scores = skms.cross_val_score(model,
                                     digits.data, digits.target,
                                     cv=10,
                                     scoring='f1_macro',
                                     n_jobs=-1) # all CPUs
    my_lbl = "{} {:.3f}".format(name, cv_scores.mean())
    ax.plot(cv_scores, label=my_lbl, marker=next(markers))
ax.set_ylim(0.0, 1.1)
ax.set_xlabel('Fold')
ax.set_ylabel('Accuracy')
ax.legend(loc='lower center', ncol=2);

Frankly, there is really too much going on here to easily summarize. Still, there are some overall trends. You can see that a classical method, Logistic Regression, is competing nicely with a very modern method, SVCs. And our drop-dead simple Nearest Neighbors methods are doing even better. It would be great practice to dive into comparing different classifiers on different metrics for this problem. You might also be interested in comparing the resource utilization of the different methods on digits.

8.8.1 Summary

We’ve now added a variety of methods to our classification toolbox. Decision trees are highly flexible models that find common regions of space. Logistic regression and discriminant analysis variations use different probabilistic models of the data to assign likelihoods to classes. Support Vector Classifiers look directly for a linear separation between classes. Along with Naive Bayes and nearest neighbors, we have eight different types of classifiers we can use.

How do we pick? Sometimes outside concerns drive our choice. Decision trees are generally readable by humans. Logistic regression models can be interpreted as the change in log-odds based on variable values. SVCs? SVCs don’t really do interpretation in the same way. We can use them, but they have a lot going on inside their black box. Now, even if we know that we need to use a DT for understanding, we might still fit other models to see how the DT performance stacks up to the other cool kids.

8.8.2 Notes

The idea that there is No One Method to Rule Them All (and in the darkness, bind them) is called the No Free Lunch Theorem. I’d prefer the No One Ring Theorem, but alas, they didn’t ask Tolkien or me.

Decision Trees While we’ve talked about decision trees leading to a class, we can also ask them about the probability distribution at the leaves. Then, if we wanted, we could flip coins to get a distribution similar to what we saw at each leaf. We don’t have to make a concrete decision if we don’t want to.

To answer the mid-tree quiz: “As the max depth increases, are we moving towards overfitting or underfitting?” The answer is overfitting.

There are several characteristics of trees that are not fundamental to DTs—they just happen to be the way things are. We could, for instance, allow decisions to be made on functions of the features. Among other things, this would allow non-parallel or non-perpendicular value splits. Instead of splitting on x > 5, we could split on 2x + 3 > 5: we now have an off-axis comparison. We could also allow comparisons like is color in {red, blue, green}? (no). We can capture that sort of relationship with a sequence of binary questions: is red? (no), is green? (no), is blue? (no). But that comes at the cost of subdividing regions that might be light on data to begin with. There is a tradeoff between expressiveness and verbosity that different authors have disagreed on. I’ll take a pragmatic approach: if you think you need a fancy technique, try it—and then cross-validate.

If you happen to be a more advanced reader making your way through this book, you might be interested in a recent (2015) paper: Efficient non-greedy optimization of decision trees by Norouzi and friends. The methods of tree-building I’ve described in this chapter are greedy: they take individual steps that seem to be the best. But, of course, without an overall map, individual steps can lead you astray. That paper describes a non-greedy way to build trees.

SVCs We’ll talk much more about some of the coolest aspects of SVMs in Chapter 13. Quickly, we move from a SVC to a SVM by introducing a kernel. To tide you over, I’ll mention that sklearn has an interface to liblinear which is a very powerful program for computing SVCs (linear SVMs) as well as logistic regression models. At a minimum, to run it as a standard SVC, comparable to what we used above, you’ll make a call like: svm.LinearSVC(loss='hinge'). The LinearSVC has some nice benefits when working with large datasets (greater than about 10,000 examples).

SVC and NuSVC use another program, libsvm, under the hood. libsvm is about as close to a de facto standard implementation of SVCs and SVMs as we have in the machine learning community. When talking about NuSVC, people often make the mistake of talking about ν in terms of training errors. ν is related to margin errors.ν is not directly related to training errors. If you want to see for yourself, read pages 1225–1226 of New Support Vector Algorithms by Scholkpf.

Trying to get LinearSVC and SVC and NuSVC to produce the same boundaries is quite difficult. libsvm and liblinear do slightly different things from a mathematical and computational perspective. At a minimum, LinearSVC includes the +1 trick column when it performs regularization. Furthermore, LinearSVC and SVC place their own defaults on top of the underlying defaults. If you want a comparison, be prepared to do some digging. These might get you started:

• https://stackoverflow.com/a/23507404/221602

• https://stackoverflow.com/q/33843981/221602

• https://stackoverflow.com/q/35076586/221602

8.8.3 Exercises

Here are some questions to keep you up at night:

1. Under what scenarios would an identifying variable, such as a unique number for each day, be useful for learning a target value? How could we apply it when we need to predict truly never-seen data—beyond even a hold-out test set?

2. Play around with SVM boundaries and example points. Make a few positive and negative examples—you can color them red and blue if you like. Make some patterns with the examples. Now, graph and look at the resulting linear boundaries that get created when you train an SVM. How do the boundaries change as you go from well-separated classes to having outliers across the obvious separation?

3. Compare the runtimes of of NuSVC and SVC under different learning scenarios and parameters.

4. Compare the DA methods with 20 repeated train-test splits. Use the same TTSs for each method. Count up the winners. Try with a different dataset.

5. You now have a bigger toolbox. Try to find better predictive models of the student data from the end of Chapter 6.

6. Our examples of bias and variance with SVCs were a bit weak. If you want to see very clear examples of bias-variance—overfitting and underfitting—redo those examples with a Gaussian kernel. Don’t know what that is? Stay tuned or turn to Chapter 13.