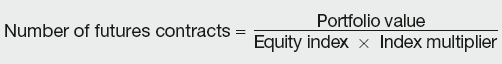10
Introduction to bond derivatives
INTRODUCTION TO BOND DERIVATIVES
In Chapter 4 on capital markets instruments, we covered bonds as a primary source of long-term funding. However, they also play a very important role in interest rate derivatives markets. They are traded both on recognised exchanges and OTC. Typical exchange-traded bond derivatives are bond futures and bond options. Various types of options and repos (repurchase agreements) are traded OTC.
Pricing bond futures
A bond futures contract is an obligation to buy/deliver a specific amount of precisely defined bond at a future date at a price agreed today. The contract can be taken to delivery, or closed out before maturity, just like other interest rate futures positions. However, the buyer can insist on bond delivery, which hugely complicates the bond futures pricing.
In practice, if a particular market-traded bond was specified for delivery, as various contracts expire, it would be possible that there wouldn’t be enough of that bond to fulfil all obligations. Hence, a notional bond paying fixed coupon and of medium maturity is typically used. The exact particulars of each notional bond are specific to each futures contract and the exchange it is traded on.
As the seller cannot deliver a fictional bond, he must choose from a range of bonds allowed for delivery under the futures contract. These bonds are called deliverable bonds. The range of deliverable bonds will include contracts of different coupons and maturities; hence some common comparison criteria are required. Each exchange thus provides a list of deliverable bonds with their respective conversion factors that make their yields equal to the notional bond coupon.
Key Point
| Conversion factor = | Deliverable bond clean unit price at which its yield is equal to the notional bond coupon |
At futures expiry, the futures price will be equal to EDSP (exchange delivery settlement price), hence the amount of bond to be delivered is:
Calculation Summary

Even though the Exchange aims to bring all the deliverable bonds to the common basis, it only publishes conversion factors periodically. Hence, at the time of delivery, it may be more favourable to deliver one bond over another, a concept known as ‘cheapest to deliver’ or CTD. The CTD bond changes with yield; when yields fall the bonds with lower duration (time until the receipt of half of the bond cashflows) become cheaper to deliver, as their prices rise less and vice versa.
Bond futures are priced using the no-arbitrage concept. Assuming that the bond will be delivered at maturity, the futures seller needs to hedge his position by buying a particular deliverable bond now. He needs to fund this purchase (cash bond price + the accrued coupon) at current prevailing interest rates. The further coupons received until maturity can be invested. Any profit/loss on the futures position is captured through the variation margin. Thus all the cashflows arising from holding the bond until delivery must be equal to the futures bond price, otherwise there would be potential for arbitrage. This can be summarised as:
Calculation Summary

The first part of the above equation refers to the funding of the initial bond purchase, whilst the second relates to the coupon cashflows. Since the futures buyer does not receive any paid and accrued coupons until delivery, this is deducted from the theoretical price.
The above formula is used by traders to calculate CTD bond.
Forward bond prices are calculated in the same way as the futures prices. However, forward contracts are obligations to deliver a particular, rather than a notional bond; hence there is no conversion factor.
Calculation Summary

Pricing repos
Repos are transactions where a transaction undertaken now is reversed in the future. In the bond market, they involve purchase/sale of a bond now and sale/purchase at a future date.
The nominal amount of the bond is the same at inception and maturity, whilst the payment at maturity incorporates interest incurred on the loan. The motivation behind this trade is either the need to borrow funds or to acquire a specific security. This is similar to a capital market loan, but as the bond is used as collateral, better rates are achieved.
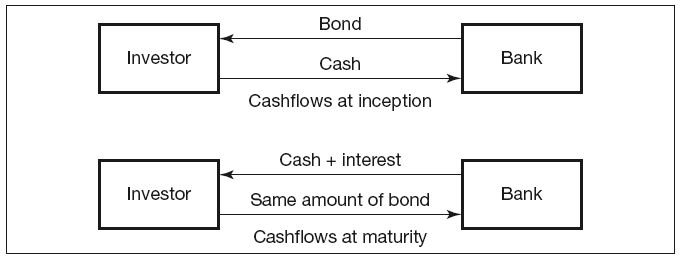
The terminology used in repo transactions is opposite to that of the cash market, the repo lender is the seller of the security (borrower of cash), whilst the repo borrower is the investor, acquiring the security in exchange for cash. The standard repo transacton at inception and maturity is graphically represented in Figure 10.1, where the bank has the role of repo lender.
Figure 10.1 Graphical representation of bond repo cashflows
Repos are valued in two parts: the initial exchange (leg) is calculated using the prevailing bond price plus accrued interest, and the reverse transaction is based on the initial leg value increased by the repo rate. This can be summarised as:
Calculation Summary

where r is the repo rate and days refer to number of days until maturity.
Pricing bond options
A bond option gives the buyer the right but not the obligation to acquire/deliver a bond at a future date for a price agreed today. The underlying security is a nominal bond with specific coupon and maturity. Pricing of various option types was discussed in the previous chapter. However, the Black–Scholes model cannot be applied directly to bond securities because of the pull-to-par effect (the bond price converges to its redemption amount at maturity). As the maturity date approaches, the factors impacting on the bond price become known with increasing certainty, thereby decreasing its volatility. This is not incorporated into the Black–Scholes model. The Black model (described in Chapter 9) addresses this problem.
Using the Black formula, the value of a bond call option is given by:
Calculation Summary: Black model for bond options
![]()
Where:
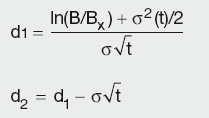
where B is the forward bond price and Bx is the underlying bond price (option strike); all other variables have the same meaning as before.
Using the put–call parity principle, the value of the put option can be derived from the value of the bond call option and the bond future price.
In most major exchanges there are option contracts on bond futures. They are priced using the Black model. The put–call parity formula is given by:
Calculation Summary: Put-call parity for bond options
where:
F is the futures price
K is the exercise price/option strike
r is the continuously compounded interest rate.
BACKGROUND ON EQUITY MARKETS
Equities are commonly thought of as stocks (American term) and shares (European term) in large corporations. A private corporation that requires funding may transact in cash or capital markets; whilst a public company, listed on an exchange, can sell shares in the stock market, also known as the equity market. This provides funding, but at a price. Shareholders become owners of the company and participate in company policy decisions and Board of Directors elections. They also share profits/losses proportionate to the number of shares they hold. For an investor shares may seem an attractive prospect, but they do not guarantee returns. Returns on shares, known as dividends, are only payable if a company is in profit. If the investment proves unprofitable, the shares have to be sold in the secondary market, as there is no redemption or maturity date. The secondary market for single-company shares is illiquid and the price achieved may not be favourable. Small investor transactions also incur brokerage fees (as exchanges are open only to their members), reducing the profits even further.
Equity indices vs. single stocks
Shares are transacted in the equity market that comprises many different sectors, each with many listed companies. An investment in shares in a single company is affected by the performance of that company alone; i.e. even if the market overall is on the rise, the company may be performing badly and no dividends are paid. Hence larger investors tend to manage diversified portfolios of shares in different sectors, hoping that by spreading the risk they will make an overall profit. They will measure the performance of the portfolio, rather than be concerned about individual shares. This concept can be extended further to measure the performance of the equity market as a whole.
The equity index or stock index mirrors the price movements of a hypothetical equity portfolio. The equities participating in the index are chosen and weighted by their market capitalisation. Thus typically only the biggest market performers are included in the index and the weighting ensures that their share price movements influence the index value proportionately. There are many equity indices in the world, each tracking the performance of the equity market in a particular country or industry sector. The main ones are listed in Table 10.1.
Stock baskets
As all the major indices are based on hypothetical portfolios with many underlying equities, they are used as a measure of overall market performance. Individual investors wishing to take a view on the equity market would find it impractical and expensive to transact in all shares comprising an index. An alternative approach is to construct a ‘basket’ of shares that would replicate the index performance with a minimum number of shares. Such portfolios are called ‘index trackers’. It can be shown that holding 20 uncorrelated shares in the basket tracks the index with a 10 per cent error margin. This number can be further reduced by careful share selection. Investment banks leave that job to quantitative analysts who develop ‘equity basket’ mathematical models. Thus an individual investor stands very little chance of making an optimal selection.
Table 10.1 Major equity indices
Baskets can be constructed to mirror index behaviour, or to speculate with the intention to outperform the market. Speculative portfolios would typically involve several high-volatility stocks that would allow for larger exposure compared to the index.
Trading in equity markets can be prohibitively expensive, or simply unsuitable for an investor’s needs. As with all other securities markets, an alternative is to trade equity derivatives. Those are off-balance sheet instruments that provide exposure to equity markets without actually owning the shares. The most commonly traded instruments are equity futures, equity options and swaps. As all other futures contracts, equity futures are exchange-traded only and are subject to same restrictions and regulations. Equity options can be traded OTC, but the market is very limited, whilst equity swaps are traded OTC only.
Stock index futures
A stock index future is a contract between two counterparties to compensate each other for the movement in the underlying equity index between the futures trade date and the settlement date. As the index is just a number, not a monetary value, in order to have practical implementations each index is assigned a monetary amount for each point of movement. This is known as an index multiplier. Hence, unlike other types of futures, equity futures contracts do not have specific contract sizes, as the value of the contract varies daily with index level and is calculated as:
Calculation Summary
Equity index futures contract size = Index level × Index multiplier
Whether a futures contract is bought or sold depends on the view of the equity market; if the investor believes that the index value will rise, he will buy the future and vice versa. Most contracts are closed out before maturity by reversing the position. Even if the future is taken to expiry, no actual shares are delivered. The difference between the futures value and the EDSP is settled. Like all other exchange-traded products, equity futures are margined, thus all but the last day’s price movements are captured through variation margin payments.
Equity futures contracts follow the same cycle as all other futures: March, June, September and December. But unlike interest rate futures that offer several years of cover, only the nearest three contracts are available for trading, with most activity in the first one.
The market participants who use equity futures are typically portfolio managers, pension funds, fund managers and other equity holders. They may transact in futures to hedge their portfolio or to speculate on market moves. To calculate how many futures a hedge requires the following formula is used:
Calculation Summary
The futures settlement price is calculated as:
Settlement amount = Number of contracts × Equity index movement × Index multiplier
The calculation of futures price follows the same logic as for any other futures contract:
Theoretical futures price = Cash price + Net cost of carry
where:
Cash price = Index level + Index multiplier
Net cost of carry = Funding cost – Dividend income
This can be summarised as:
Calculation Summary
where:
i is the annual funding rate
d is the dividend yield on underlying equity.
Stock beta
Constructing a portfolio that would exactly replicate the index performance is not easy; thus a hedge using an equity index future will be imperfect, as the two values will move out of line. Stock beta gives a measure of individual stock volatility compared to the index. It is assigned by the exchange to each listed equity and the information is disseminated through the market information network. The portfolio beta is then derived as a capital-participation weighted average of individual share betas, i.e.:
Calculation Summary
where:
βi is the individual equity beta
Vi is the individual equity share value
VP is the total value of the portfolio.
Incorporating beta into the hedging strategy changes the amount of futures that need to be bought to:
Calculation Summary

An important point has to be made here. Betas are used to track the performance of a particular portfolio to an index. The index is a very close representative of the overall market performance, but at times it may move out of line with the market as a whole. This may cause problems to portfolio managers who are required to pay inflation-linked pensions or other instruments linked to the country’s economy. They may deliberately choose not to track the index perfectly but to include some more volatile stocks, hoping that the potential increased profit will provide the sufficient tracking-error margin.
Stock index options
As the OTC market for equity index options is very limited, this section will concentrate on exchange-traded options.
The stock index option gives the holder the right but not the obligation to buy/sell a specified amount of the equity index (index level × index multiplier) at or before a specified future date. The premium is paid up-front and the contract is cash-settled, i.e. the equities underlying the index are not delivered. As with all option contracts, the option buyer chooses the option strike; in this case, the specific index level. This influences the required premium due, which is quoted as index points. Its monetary amount is based on the index multiplier, which is exchange-specific and may be different to the one used for futures contracts. The same principles underlying all exchange-traded products and the characteristics of option contracts discussed in previous chapters still apply.
Call option valuation is typically done using the Black–Scholes formula:
Calculation Summary: Black–Scholes for equity index options
![]()
where the dividend yield d is assumed to be paid continuously.
The put price is then calculated using put–call parity:
Calculation Summary: Put–call parity for equity index options
![]()
Single stock options
Single stock options are contracts that give the holder the right but not the obligation to buy/sell a specified amount of the underlying equity at a price agreed today on or before a specified future date. The premium is paid up-front and the contract is physically settled, i.e. the equity shares are delivered. They provide a useful tool for portfolio diversification, both for hedging and speculating purposes. The equities underlying exchange-traded options are specific to each exchange. The options positions can be closed out before expiry by reversing the transaction. This is the common practice of speculators, who trade for profit only and do not require the actual shares. The same principles underlying all exchange-traded products and the characteristics of option contracts discussed in previous chapters still apply.
Call option valuation is typically done using the Black–Scholes formula:
Calculation Summary: Black–Scholes for single stock options
![]()
where dividend payments until expiry are captured by reducing the stock price by the present value of dividends. This is known as the ‘known dividend model’.
The put price is then calculated using put–call parity:
Calculation Summary: Put–call parity for dividend-paying single stocks
![]()
where D is the present value of expected dividend.
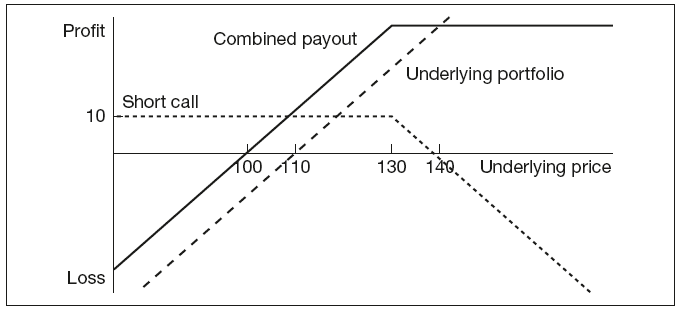
Different strategies, discussed in Appendix 1, can be used depending on the client’s view of the stock market. For example, hedgers who believe that the prices of the stock they already hold will not fluctuate by much can take advantage of the ‘covered call’ strategy, i.e. they will sell calls on stocks they already have. The strike price is set above the current share price. If the stock value declines, the option will be abandoned and the premium income will provide a level of downward protection. If the price increases below the exercise level, the portfolio profits both from the market move and the full premium income. Only in the event of an unexpectedly large increase in the share price is the fund manager’s strategy less profitable than the underlying position. This can be seen in Figure 10.2.
Figure 10.2 Payout profile of stock option covered call strategy
Equity index swaps
An equity index swap is an OTC contract between two counterparties to exchange cashflows at regular intervals for a time period where at least one leg is based on the percentage change in the value of a chosen equity index. The second leg, if not derived from stock index value, is typically related to a floating interest rate, such as Libor. The swap is based on a notional principal and is cash-settled (see Figure 10.3).
Figure 10.3 Graphical representation of equity index swap
Equity index swaps are very useful investment tools for market participants that find it impractical or impossible to trade equities directly. Some of the main characteristics are discussed below:
Cash settlement reduces the counterparty risk, as no principals are exchanged.
Synthetic stock market investment is implicit in the swap; the exchange of interest rate cashflows for index tracking creates stock market exposure without actually having to buy stocks.
Cost of carry is eliminated; as stocks are not bought, there is no requirement to pay costs associated with holding shares (stamp duty, taxes etc.).
Income enhancement for fund managers who hold equities they believe will depreciate is provided by a swap of equity index into a floating interest rate or other type of cashflow.
Exposure to foreign index that otherwise may not be permissible is synthetically generated by a swap of domestic index movements for foreign index fluctuations.
Portfolio management burdens are eliminated by entering into a swap, as the responsibility is passed to the swap issuer. The portfolio manager can in this way stabilise portfolio returns without the need to change its underlying components.
Equity index swaps are priced using the same principles as other swap types, i.e. based on the concept that the NPV of both legs of the swap has to be equal at inception. More details were provided in Chapter 7.
Calculation Summary: Equity index swap valuation
PV(Swap) = PV(equity index leg) − PV(floating leg) = 0