3
Solution of System of Linear Algebraic Equations
3.0 INTRODUCTION
Very often we encounter simultaneous linear equations in various fields of science and engineering. We have seen the analysis of electronic circuits consisting of invariant elements ultimately depend on the solution of such equations by determinant and matrix methods. These methods become tedious for large systems of equations. To solve such equations there are numerical methods which are suitable for computations using computers. The methods of solution of linear algebraic equations may broadly be classified into two types, namely, direct methods and indirect methods.
Direct methods produce exact solution after a finite number of steps (disregarding round off errors). So direct method is also known as exact method.
Indirect methods give a sequence of approcimate solutions, which ultimately approach the actual solution. Iterative method is some times referred to as indirect method.
In this chapter, we also consider eigen value problems and method of factorisation or method of triangularisation to solve the system of equations.
3.1 DIRECT METHODS
3.1.1 Matrix Inverse Method
Consider the system of n linear equations in n variables ![]()
 (1)
(1)
 ,
,  and
and 
Then the system (1) can be written as a single matrix equation as
![]() (2)
(2)
If A is non-singular, then ![]() and the inverse matrix
and the inverse matrix ![]() exists and
exists and ![]()
where

![]() Mij and Mij is the minor of aij in
Mij and Mij is the minor of aij in ![]() .
.
Pre multiplying (2) by ![]() we get
we get
 is the solution of (1)
is the solution of (1)
WORKED EXAMPLES
Example 1
Solve the system of equations ![]() ;
; ![]() ;
; ![]() .
.
Solution
Given system is

Here

 and
and 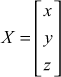
Now
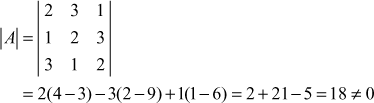
![]() exists and
exists and ![]()
Now



∴ 
∴ 
∴ the solution is ![]()

∴ the solution is ![]()
Example 2
Solution
Given system is

Here
 and
and 
∴ the given system is AX= B.
Now

![]() exists and
exists and ![]()
Now


∴ the solution is ![]()
⇒
⇒
⇒
∴ the solution is ![]() ,
, ![]() ,
, ![]()
3.1.2 Gauss Elimination Method
It is a direct method. In this method the unknowns are eliminated in such a way the n equations in n unknowns are reduced to an equivalent upper triangular system which is then solved by back substitution. The method is explained below.
For simplicity, we shall consider a system of 3 equations in 3 unknowns ![]() .
.
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
Let 
Then the system of equations can be written as a single matrix equation AX = B
The augmented matrix is 
First step is to eliminate x1 from the 2nd and 3rd equation.
So we multiply (1) by ![]() and add with (2).
and add with (2).
If ![]() then multiply (1) by
then multiply (1) by ![]() and add with (3).
and add with (3).
Then ![]() will be eliminated from (2) and (3).
will be eliminated from (2) and (3).
We will get an equivalent system.
![]() is called the first pivot and the equation (1) is called the pivotal equation.
is called the first pivot and the equation (1) is called the pivotal equation.
In case ![]() , we interchange the equations and take the equation for which coefficient of
, we interchange the equations and take the equation for which coefficient of ![]() as the first equation.
as the first equation.
∴ the augmented matrix will become
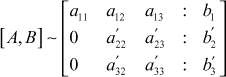
Now the second step is to eliminate x2 from the new third equation (or third row in the matrix). For this ![]() is the new pivot or second pivot.
is the new pivot or second pivot.
Multiply the second row by ![]() and add to third row.
and add to third row.
So, at the end of second step

Thus the equations are reduced to an equivalent system of equations.

From third equation we get x3, which can be substituted back in 2nd equation we get x2 and then from the first equation we get x1.
This elimination procedure is known as Gauss elimination method.
Partial pivoting: In the first step of elimination, the first column is searched for the numerically largest element and brought it as the first pivot by interchanging the rows. In the second step of elimination, the second column is searched for the numerically largest element among the remaining ![]() elements (leaving the first row) and it is brought as the 2nd pivot by interchange and so on. This procedure is continued and the coefficient matrix is reduced to an upper triangular matrix. This modified form of elimination is known as partial pivoting. This method ensures that errors are not propagated by large multipliers.
elements (leaving the first row) and it is brought as the 2nd pivot by interchange and so on. This procedure is continued and the coefficient matrix is reduced to an upper triangular matrix. This modified form of elimination is known as partial pivoting. This method ensures that errors are not propagated by large multipliers.
Complete pivoting: We search the coefficient matrix A for the numerically largest element and brought it as the first pivot, by suitable interchanges of rows and also interchange of position of the elements. At each step if we adopt this procedure the method is known as complete pivoting. But, this procedure is complicated and it does not improve accuracy appreciably.
WORKED EXAMPLES
Example 1
Solve by Gauss elimination method the equations 2 x + y + 4 z = 12; 8 x - 3 y + 2 z = 20; 4 x + 11 y - z = 33.
Solution
Given system is

The augmented matrix is

∴ the equivalent reduced equations are
![]()
∴ 
∴ the solution is ![]()
Example 2
Solve the equations ![]() by Gauss elimination method.
by Gauss elimination method.
Solution
Given system is

We shall rearrange the equations as

The augmented matrix is

∴ the equivalent equations are

∴ ![]()
![]()
∴ the solution is ![]()
Example 3
Solve by Gauss elimination method the equations x 1 + x 2 + x 3 + x 4 = 2; x 1 + x 2 + 3 x 3 − 2 x 4 = −6; 2 x 1 + 3 x 2 − x 3 + 2 x 4 = 7; x 1 + 2 x 2 + x 3 − x 4 = −2.
Solution
Given system is

The augmented matrix is


∴ the equivalent reduced equations are



∴ the solution is ![]()
3.1.3 Gauss-Jordan Method
This is a direct method which is a modification of Gauss elimination method. After eliminating one variable by Gauss elimination method, in the subsequent stages the elimination is performed not only in the equations below but also in the equations above. Thus the coefficient matrix is reduced to a diagonal matrix and hence the values of the unknowns are readily obtained. This modification is due to Jordan and hence it is known as Gauss-Jordan method.
Note: For large system of equations the number of algebraic operations involved in this method is more and so Gauss elimination method is preferred.
WORKED EXAMPLES
Example 1
Solve by Gauss-Jordan method the equations x + y + z = 9; 2 x − 3 y + 4 z = 13; 3 x + 4 y + 5 z = 40.
Solution
Given system is

The augmented matrix is

∴ the solution is ![]()
Example 2
Using Gauss-Jordan method solve 10 x + y + z = 12; 2 x + 10 y + z = 13; x + y + 5 z = 7.
Solution
Given system is>


Rearranging the equations, we get

The augmented matrix is

∴ the solution is ![]()
Example 3
![]()
Solution
Given system of equations is

The augmented matrix is


∴ the solution is ![]()
Example 4
Solve the linear system ![]()
![]()
![]()
![]()
by Gauss-Jordan method.
Solution
Given system is

Rearranging the system, we get

The augmented matrix is




∴ the solution is ![]()
3.1.4 Matrix Inverse by Gauss-Jordan Method
We shall explain the method for 3 × 3 matrix.

If A is non-singular, then there exists a 3 × 3 matrix

such that AX = I
⇒ 
This equation is equivalent to the three equations below:
 (1)
(1)
 (2)
(2)
and
 (3)
(3)
Equation (1) is a system of linear equations. Solving by Jordan’s method (or by Gauss elimination method) we get ![]() and so the vector
and so the vector ![]() is known. Similarly solving (2) and (3) we get the other columns of X and hence X is known. This matrix X is the inverse of A.
is known. Similarly solving (2) and (3) we get the other columns of X and hence X is known. This matrix X is the inverse of A.
Now to solve the equation (1), we start with the augmented matrix ![]() where
where  and transform by row operations so that A is reduced to unit matrix in Jordan’s method, then we write the solution for
and transform by row operations so that A is reduced to unit matrix in Jordan’s method, then we write the solution for ![]() directly.
directly.
The same procedure is applied to solve (2) and (3) by writing ![]() and
and ![]() .
.
In practice we will not do this individually and convert A into a unit matrix, but we start with ![]() and convert A into unit matrix by row operations and find X.
and convert A into unit matrix by row operations and find X.
Working Rule
Consider the augmented matrix [A, I ], where I is the identity matrix of the same order as A. By row operations reduce A into a unit matrix, then correspondingly I will be changed into a matrix X. This matrix X is the inverse of A. It is advisable to change the pivot element to 1 before applying row operations at each step.
WORKED EXAMPLES
Example 1
Using Gauss-Jordan method, find the inverse of the matrix 
Solution
Given

Consider the augmented matrix

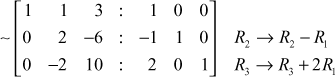
 (The pivot 2 in R2 is reduced to 1)
(The pivot 2 in R2 is reduced to 1)

 (The pivot 2 in R3 is reduced to 1)
(The pivot 2 in R3 is reduced to 1)

∴ the inverse matrix of A is 
Example 2
Find the inverse of the matrix 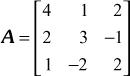 by Gauss-Jordan method.
by Gauss-Jordan method.
Solution
Given

Consider the augmented matrix

 ( The pivot 4 in R1 is reduced to 1)
( The pivot 4 in R1 is reduced to 1)
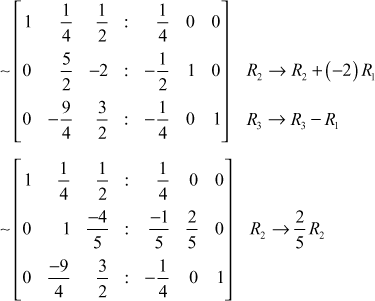 ( The pivot
( The pivot ![]() in R2 is reduced to 1) ( The pivot
in R2 is reduced to 1) ( The pivot ![]() in R3 is reduced to 1)
in R3 is reduced to 1)

∴ the inverse of A is 
Example 3
Solve the system of equations ![]() by finding the matrix inverse by Gauss-Jordan method.
by finding the matrix inverse by Gauss-Jordan method.
Solution
The given system of equations is

The coefficient matrix is

∴ the system of equations is ![]()
We find ![]() by the method of matrix inverse by Gauss-Jordan method.
by the method of matrix inverse by Gauss-Jordan method.
Consider the augmented matrix


∴ the inverse is

∴![]()

∴ the solution is ![]()
Example 4
Solve the system of equations ![]() by finding the inverse by Gauss-Jordan method.
by finding the inverse by Gauss-Jordan method.
Solution
The given system of equations is

The coefficient matrix is

∴ the system of equation is ![]() ∴
∴ ![]()
We find ![]() by the method of matrix inverse by Gauss-Jordan method.
by the method of matrix inverse by Gauss-Jordan method.
Consider the augmented matrix


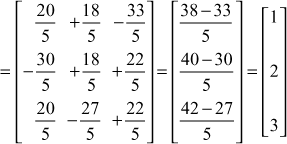
∴ the solution is ![]()
Exercises 3.1
- (I) Solve by matrix inversion the following system of equations.
- (II) Solve by Gauss-elimination method.
- (III) Solve using Gauss-Jordan method.
- (IV) Find the Matrix Inverse by Gauss-Jordan method.
 (20)
(20) 
 (22)
(22) 
- (23)
 (24)
(24) 
- (25) Solve the system of linear equations
 finding the inverse matrix by Gauss-Jordan method.
finding the inverse matrix by Gauss-Jordan method. - (26) Solve the system of equations
 , finding the inverse matrix by Gauss-Jordan method.
, finding the inverse matrix by Gauss-Jordan method.
Answers 3.1
- (I)
(1)
 (2)
(2) 
(3)
 (4)
(4) 
(5)

- (II)
(6)
 (7)
(7) 
(8)
 (9)
(9) 
(10)
 (11)
(11) 
(12)

- (III)
(13)
 (14)
(14) 
(15)
 (16)
(16) 
(17)
 (18)
(18) 
- (IV)
(19)
 (20)
(20) 
(21)
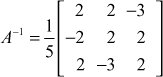 (22)
(22) 
(23)
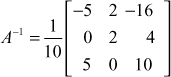 (24)
(24) 
(25)
 (26)
(26) 
3.2 ITERATIVE METHODS
We have seen iteration is a successive approximation method. We start with an approximate solution and obtain a sequence of better approximations and stop at the step when two consecutive approximations coincide upto the desired degree of accuracy. The iterative method succeeds if the sequence of approximate solutions approach the actual root. For the iteration method to succeed, each equation of the system must possess one large coefficient and the large coefficient must be attached to different unknowns in the system. In other words, the coefficient matrix A is diagonally dominant.
The system of equations

will be solvable if ![]()
For example, the system of equations

as such is not diagonally dominant. But it can be rearranged as

This is a diagonally dominant system or the coeff icient matrix

3.2.1 Gauss-Jacobi Method
Consider the system

We shall assume the system is diagonally dominant,
ie. ![]()
The system can be rewritten as

Let ![]() be the initial values of x, y, z.
be the initial values of x, y, z.
Then I Iteration is

II Iteration is

and proceed this way until we reach the solution.
Note: In the absence of better estimates for the initial values ![]() , we take them as 0, 0, 0.
, we take them as 0, 0, 0.
WORKED EXAMPLES
Example 1
Solve the system of equation correct to 3 decimal places using Jacobi method.
x + 17 y – 2 z = 48; 30 x – 2 y + 3 z = 75; 2 x + 2 y + 18 z = 30
Solution
The equations in diagonally dominant form is

In Jacobi method for every iteration, the previous iteration values are used.
Initially take
![]()
I Iteration:

II Iteration:

III Iteration:

IV Iteration:

V Iteration:
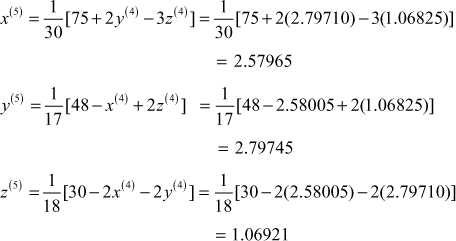

∴ the solution correct to 3 decimal places is
![]()
3.2.2 Gauss-Seidel Method
Gauss-Seidel method is a refinement of Gauss-Jacobi method.
Consider the system of equations

we shall assume the system is diagonally dominant,
ie. ![]()
The system can be written as

We start with the initial approximation ![]()
I Iteration:

II Iteration:

At each iteration we use the latest available approximations for x,y,z. So, this method converges faster than the Jacobi method.
Note:
- It is found that the Gauss-Seidel iteration method is at least twice as fast as the Jacobi iteration method. So, we use Gauss-Seidel method when the method is not specified.
- Iteration is a self correcting method. Errors of computations made at a step will not affect the final answer, the number of iterations may be increased.
- In Gauss-seidel method if A is diagonally dominant, then the iteration scheme converges for any initial values of the variables.
WORKED EXAMPLES
Example 1
![]()
Solution
We note that the largest coefficient is attached to different variables in different equations.
Also this largest coefficient is numerically larger than the sum of the other two coefficients. So, iteration method can be applied. Rearranging the equations in diagonally dominant form we have

Initially take ![]()
I Iteration:

II Iteration:
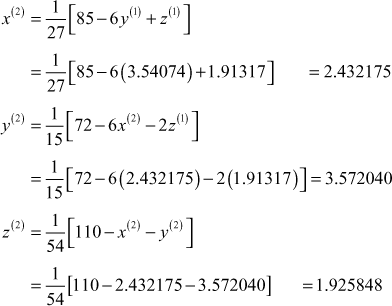
III Iteration:

IV Iteration:

V Iteration:


From the table of values we notice that the 4th and 5th iterations coincide upto 4 places of decimals.
So, the solution is x = 2.42548, y = 3.57302, z = 1.92595
Example 2
Apply Gauss-Seidel method to solve the system of equations 20 x + y – 2 z = 17; 3 x + 20 y – z = –18; 2 x – 3 y + 20 z = 25.
Solution
We note that the largest coefficient is attached to different variables in the different equations. So the given equations are diagonally dominant.

Initially take ![]()
I Iteration:

II Iteration:

III Iteration:


We shall take the solution as ![]()
It is easily verified that it is the exact solution.
Example 3
Solve by Gauss-Seidel iteration the given system of equations starting with (0, 0, 0, 0) as solution. Do 5 iterations only. 4 x 1 - x 2 - x 3 = 2; - x 1 + 4 x 2 - x 4 = 2; - x 1 + 4 x 3 - x 4 = 1; - x 2 + x 3 + 4 x 4 = 1.
Solution
The given equations are diagonally dominant.
∴ 
Initially, take ![]()
I Iteration:

II Iteration:

III Iteration:

IV Iteration:

V Iteration:


∴ the solution is ![]()
Exercises 3.2
Solve by Gauss-Seidel iteration method or Jacobi method
Solution

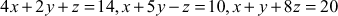
 starting with
starting with 








Answers 3.2
- x1 = 2, y = 1, z = 3 (2) x = y = z = 2
- x = 1.23, y = −2.34, z = 3.45 (4) x = 0.3416, y = 0.2851, z = −0.50
- x = 3, y = 2, z = 1 (6) x = 1, y = −2, z = 3
- x = 1, y = −2, z = 1 (8) x = 1, y = 2, z = 3
- x = 2, y = 1, z = 3 (10) x = −13.223, y = 16.766, z = −2.306
3.3 EIGEN VALUE PROBLEM
The problem of determining the eigen values and eigen vectors of a square matrix is known as eigen value problem. This problem occurs frequently in physical and engineering problems.
Definition: Let A be a ![]() square matrix. A number
square matrix. A number ![]() is called an eigen value of A if there exists a non-zero
is called an eigen value of A if there exists a non-zero ![]() column matrix X such that
column matrix X such that ![]() .
.
Then X is called an eigen vector of A corresponding to the eigen value l.
3.3.1 Power Method
In practical applications, quite often, it is required to find the numerically largest eigen value. The power method is a simple iterative method which enables us to find the approximate value of the numerically largest eigen value of A. We shall discuss the method.
Let ![]() be the distinct eigen values of A and let
be the distinct eigen values of A and let ![]() . So
. So ![]() is the dominant eigen value of A. Let
is the dominant eigen value of A. Let ![]() be the corresponding eigen vectors.
be the corresponding eigen vectors.
Then ![]() .
.
Note that the Xi are n-component column vectors.
The method is applicable if the complete set of n eigen vectors are linearly independent. Then any vector X(0) in the space of the eigen vectors ![]() can be written as
can be written as
![]()
where ![]() are constants.
are constants.
Premultiplying by A, we get,

Again applying A and simplifying we get

⇒![]() , where
, where ![]() .
.
Proceeding this way, after m such multipliers, we get
![]()
Since ![]() is numerically largest, taking out
is numerically largest, taking out ![]() we get
we get

Since ![]() for all
for all ![]() we get
we get  as
as ![]()
∴ as ![]() ,
, ![]() if
if ![]() and so
and so ![]() is a multiple of the eigen vector
is a multiple of the eigen vector ![]() .
.
The vector 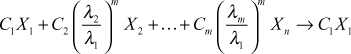 ;
;
which is an eigen vector corresponding to ![]() .
.
The eigen value ![]() is obtained as the ratio of the corresponding components of
is obtained as the ratio of the corresponding components of ![]() and
and ![]()

where the suffix r denotes the rth component of the vector.
Note:
- If
 is much smaller than
is much smaller than  , then the convergence will be faster.
, then the convergence will be faster. - In order to keep the round off error in control, we normalise the vector (such that the largest element is 1) before premultiplying by A.
- If another eigen value is nearer to
 , then convergence will be very slow.
, then convergence will be very slow. - Finding the largest eigen value when the roots are not different is beyond the scope of this book.
Working rule to find the largest eigen-value (numerically)
- Let X0 be the initial vector which is usually chosen as a vector with all components equal to 1 (i.e. normalised).
ie.

- Form the product AX0 and express it in the form
 , where X1 is normalised by taking out the largest component
, where X1 is normalised by taking out the largest component 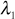 .
. - Form
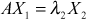 , where
, where  is normalised in the same way and continue the process.
is normalised in the same way and continue the process. - Thus we have a sequence of equations
 We stop at the stage where
We stop at the stage where  are almost same.
are almost same.
Then ![]() is the largest eigen value and Xr is the corresponding eigen vector.
is the largest eigen value and Xr is the corresponding eigen vector.
To find the numerically smallest eigen value of A
Method (1): Obtain the dominant eigen value ![]() of A and the dominant eigen value
of A and the dominant eigen value ![]() of
of ![]() . Then the numerically smallest eigen value of A is
. Then the numerically smallest eigen value of A is ![]()
Method (2): Find the dominant eigen value ![]() of A–1 and then
of A–1 and then ![]() is the smallest eigen value of A.
is the smallest eigen value of A.
WORKED EXAMPLES
Example 1
Find the larger eigen value of the matrix  and compare your result with the explicit solution of the characteristic equation.
and compare your result with the explicit solution of the characteristic equation.
Solution
Let ![]()
The characteristic equation of A is


Characteristic equation is

∴ the largest eigen value is ![]()
We shall now find the largest eigen value by the iterative power method.
Take  as the initial vector.
as the initial vector.
Then


We find the eigen value is 4.618 correct to 3 places of decimal and the eigen vector is ![]()
The largest eigen value due to explict method and power method are the same.
Example 2
Find the numerically largest eigen value of 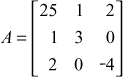 and the corresponding eigen vector.
and the corresponding eigen vector.
Solution
Given
 . Take
. Take  as the initial vector.
as the initial vector.
Then

where

Since
![]() we stop the iteration and the largest eigen value is 25.1821 and the corresponding eigenvector is
we stop the iteration and the largest eigen value is 25.1821 and the corresponding eigenvector is

Example 3
Find the smallest eigen value of 
Solution
We shall use method (2) That is we shall find the largest eigen value of A−1
Given 
then ![]()

Take  as the initial vector
as the initial vector
Then

Now

Since ![]() , we stop the iteration and take
, we stop the iteration and take ![]() as the largest eigen value of
as the largest eigen value of ![]()
∴ the numerically smallest eigen value of A is ![]()
Example 4
Using power method, find all the eigen values of 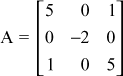
Given

First we shall find the numerically largest eigen value.
Let  be the initial vector.
be the initial vector.


Approximating to 2 decimals –0.002 is taken as 0, the dominant eigen value of A is
![]() and the corresponding vector is
and the corresponding vector is ![]()
To find the smallest eigen of A we shall use method (1). So, we form the matrix
 and find the numerically largest eigen value of B.
and find the numerically largest eigen value of B.
Take  as the initial vector.
as the initial vector.
Then

Since ![]() we stop the iteration and
we stop the iteration and ![]() as the dominant eigen value of B.
as the dominant eigen value of B.
∴ the smallest eigen value of A is ![]()
If λ is the third eigen value, then the eigen values of A are 6, –2, λ

∴ the eigen value of A are 6, 4, –2.
Exercises 3.3
- Obtain by power method, the numerically largest eigen value of the matrix
 .
. - Obtain the largest eigen value and the corresponding eigen vector of the matrix
 .
. - By power method find the largest (numerically) eigen value of the matrix
 . Also the corresponding eigen vector.
. Also the corresponding eigen vector. - Find the dominant eigen value and the corresponding eigen vector of the matrix
 .
. - Find the dominant eigen value and the corresponding eigen vector of the matrix
 .
. - Find the dominant eigen value and eigen vector of the matrix
 by power method and hence find all the eigen values.
by power method and hence find all the eigen values.
Answers 3.3
- –20 (2) 3.41;
 (3) 7;
(3) 7; 
- 8;
 (5) 11.66;
(5) 11.66;  (6) 7;
(6) 7;  and 1, – 4
and 1, – 4
3.3.2 Jacobi’s Method to Find the Eigen Values of a Symmetric Matrix
Let A be a real symmetric matrix. We know that the eigen values of a real symmetric matrix are real and there exists an orthogonal matrix S such that S–1 AS is a diagonal matrix D-whose diagonal elements are the eigen values of A.
But in Jacobi’s method the matrix S is formed by a series of orthogonal transformations (or orthogonal matrices) ![]() such that
such that ![]() . In this method we make all the off-diagonal elements of A as zero in a systematic way as below.
. In this method we make all the off-diagonal elements of A as zero in a systematic way as below.
Let ![]() be
be ![]() matrix.
matrix.
Among all the off-diagonal elements of A, choose the numerically largest element. Let aik be the element such that |aik| is largest. Form a 2 × 2 submatrix with the elements ![]() .
.
Let  .
.
Since A is symmetric ![]() and so
and so ![]() is symmetric.
is symmetric.
Let ![]() be the orthogonal matrix which transforms
be the orthogonal matrix which transforms ![]() into a diagonal matrix.
into a diagonal matrix.
Now ![]()
![]()

 (1)
(1)
Since this a diagonal matrix, we have

We shall choose the principal value of q. ie. ![]()
∴  (2)
(2)
If ![]() , then
, then  (3)
(3)
When θ is given by (2) or (3) the off-diagonal elements of the matrix (1) are zero and the diagonal elements are simplified.
Geometrically, the matrix  represents the transformation rotation in the plane. Thus by performing a two-dimenstional rotation, we make the
represents the transformation rotation in the plane. Thus by performing a two-dimenstional rotation, we make the ![]() element 0. Since
element 0. Since ![]() , the rotation is the smallest.
, the rotation is the smallest.
Now coming back to the main problem, if ![]() is the numerically largest off-diagonal element, then the first rotation matrix
is the numerically largest off-diagonal element, then the first rotation matrix ![]() is taken as
is taken as

where the elements in the positions (i , i), (i , k), (k, i), (k, k) are ![]() and
and ![]() is found by (2) or (3) and all other elements are 1 or 0 as in a unit matrix.
is found by (2) or (3) and all other elements are 1 or 0 as in a unit matrix.
Let ![]()
Next we find the largest off-diagonal element in B1 and proceed as above with B1 in the place of A.
Let S2 be the second rotation matrix then
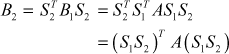
Proceeding like this, we get
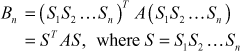
When n is large (ie. ![]() ) Bn approaches a diagonal matrix whose diagonal elements are eigen values of A. The corresponding eigen vectors are the respective columns of
) Bn approaches a diagonal matrix whose diagonal elements are eigen values of A. The corresponding eigen vectors are the respective columns of ![]()
Note:
- The minimal number of rotations (or transformations) requited to bring A into diagonal form is
 .
. - The drawback of Jacobi’s method is that the clement made 0 by a transformation may not remain 0 during the subsequent transformations.
- The value of θ must be checked with
 for the sake of accuracy.
for the sake of accuracy.
WORKED EXAMPLES
Example 1
Using Jacobi’s method find the eigen values and eigen vectors of ![]() .
.
Solution
Let ![]()
The largest off-diagonal element is ![]()
The rotation matrix ![]()
Since ![]() and
and ![]() we have
we have ![]()
∴ 
Then the transformation (or rotation) gives

This is a diagonal matrix. So, the eigenvalues are 3, –1 and the corresponding eigen vectors are the columns of S1. ie. 
Note: These eigen vectors are normalised. The eigen vectors are also given as ![]()
Example 2
Using Jacobi’s method, find the eigen values and eigen vectors of ![]() .
.
Solution
Let ![]()
The largest off-diagonal element is ![]()
And ![]() . Here
. Here ![]()
Let ![]() be the rotation matrix.
be the rotation matrix.
Since ![]()
Here θ is not a familiar angle. So we proceed as below.
We know ![]()


Since θ is the smallest rotation, ![]()
![]()
∴
Then the transformation ![]()
⇒ 
Thus B1 is diagonal matrix.
So the eigen values of A are 3, –2 and the corresponding eigen vectors are the columns of S1.
ie.  or
or ![]()
Example 3
Using Jacobi’s method find all the eigen values and eigen vectors of the matrix  .
.
Solution
Let 
The largest off-diagonal element is ![]() and
and ![]()
The first rotation matrix S1 will have the (1, 1), (1, 3), (3, 1), (3, 3) positions ![]() and other places 0 or 1 as in a unit matrix.
and other places 0 or 1 as in a unit matrix.
∴ 
Since ![]() and
and ![]()

∴ the first transformation or rotation gives

This is not a diagonal matrix. So we make a second rotation or transformation.
The largest off-diagonal element in B1 is ![]() and
and ![]()
The second rotation matrix is 
Since ![]() and
and ![]()
∴ 
The second transformation gives


∴ the eigen values are 5, 1, –1.
Now

∴ the corresponding eigen vectors are

Example 4
Using Jacobi’s method, find all the eigen values and eigen vectors of the matrix  .
.
Solution
Let 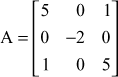
The largest off-diagonal element is ![]()
The first rotation matrix 
Since ![]() , we have
, we have ![]()
∴
∴ the first transformation matrix gives

Thus by a single transformation, A is reduced to diagonal form.
∴ The eigen values are 6, –2, 4 and the eigen vectors are the columns of S1
ie.  or
or 
Exercises 3.4
By Jacobi’s method find all the eigen values and the corresponding eigen vectors of the matrices.
 (2)
(2)  (3)
(3) 
 (5)
(5) 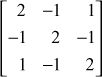
Answers 3.4
- (1)
 (2)
(2)  (3)
(3) 
 (5)
(5) 
3.4 METHOD OF FACTORISATION OR METHOD OF TRIANGULARISATION
Let ![]() represent a system of linear equations. We factorise A as
represent a system of linear equations. We factorise A as ![]() , where L is a lower triangular matrix and U is an upper triangular matrix.
, where L is a lower triangular matrix and U is an upper triangular matrix.
For simplicity we consider A as 3 × 3 matrix.
∴
Let  and
and 
Then ![]()
Equating the elements in A = LU, we will get 9 equations in 12 unknowns (6 lij’s and 6 uij’s) So, it is not possible to get the unique solution.
In order to get unique solution, we have to f ix values for 3 unknowns, so that there are 9 equations in 9 unknowns.
To obtain unique solution
Doolittle chose ![]() ie L is chosen as unit lower triangular matrix and U is an upper triangular matrix.
ie L is chosen as unit lower triangular matrix and U is an upper triangular matrix.
Crout chose ![]() so that U is unit upper triangular matrix and L is a lower triangular matrix.
so that U is unit upper triangular matrix and L is a lower triangular matrix.
But the LU Decomposition exists if the principal minors of the matrix A are non-singular.
That is

Such a factorisation is unique. However, it is only a sufficient condition.
This method is also known as LU Decomposition method.
3.4.1 Doolittle’s Method
Consider the equations

Here

![]()
Let ![]() , where
, where 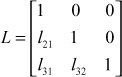 and
and 
Then ![]() .
.
Put ![]() , where
, where  , then
, then ![]()
Since L and B are known, Y is known.
Substitute in ![]() .
.
Then U and Y are known and so X is known.
Substitute in ![]()
Then U and Y are known and so X is known.
Note:
(1) In this method, to find the elements of L and U, we equate the corresponding row elements of A and LU.
(2) ![]() can also be determined, since
can also be determined, since ![]()
WORKED EXAMPLES
Example 1
Solve the linear system of equations ![]()
![]() by factorisation method.
by factorisation method.
Solution
The given system of equations is

Here
 and
and 
![]() the given system is AX = B.
the given system is AX = B.
We solve the system by Doolittle’s method ![]() we take
we take ![]()
where
 and
and 
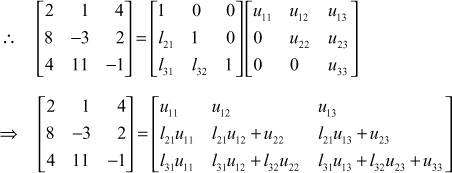
Equating the elements of I rows, we get ![]()
Equating the elements of II rows, we get
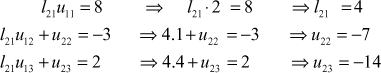
Equating the elements of III rows, we get

∴ 
∴![]()
Put 
∴ LY = B
⇒
⇒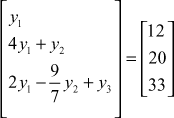
⇒
and
![]()
⇒



∴ the solution is ![]()
Example 2
Factorise the matrix  and hence solve the system of equations.
and hence solve the system of equations. ![]()
![]()
Solution
Let 
We factorize A using Doolittle’s method. ![]() we take
we take ![]() ,
,
where  and
and 
∴ 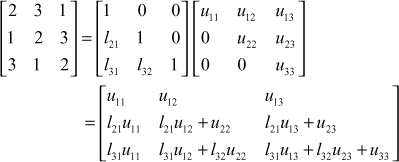
Equating elements of first rows, we get
![]()
Equating elements of second rows, we get
![]()
⇒
Equating elements of III rows, we get

and

∴ and
and 
Given system is

The coefficient matrix is 
which is same as A
∴ the matrix equation is ![]() , where
, where  and
and 
Now ![]()
Put ![]() , then
, then ![]() where
where 
∴LY = B
⇒
⇒
⇒ 
∴
Now UX = Y
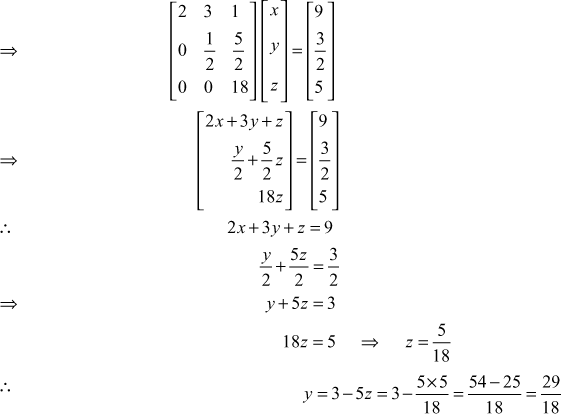
and

∴ the solution is ![]()
Example 3
(a) Find the matrices L and R such that LR = A , where
 and
and 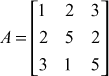
(b) A system of equations is given by A X = B , where X = { x 1 , x 2 , x 3 } B = { 14, 18, 20 } . Rewrite the equation A X = B as L Z = B and R X = Z where Z = { z 1 , z 2 , z 3 } and for X , determining Z first, the matrices L , R , A being as given in (a).
Solution
(a) Given

By Doolittle’s method, we factorize A and we take A= LR

Equating the corresponding elements row wise on both sides, we get

∴  (3)
(3)
(b) Given AX = B, LZ = B and RX = Z
where  , L and R are given by (3),
, L and R are given by (3),
 and
and 

∴z1 = 14
2z1 + z2 = 18
3z1 2z2 + z3 = 20
∴ 2z1 = 18 = 18 − 28 = − 10

Now ![]()


and ![]()
∴ the solution is ![]()
Example 4
Solve the system of equations by Doolittle’s method.
![]()
Solution
The given system of equations is

Here

∴ the given system is AX = B (1)
By Doolittle’s method, we take A = LU
where
 and
and 
∴AX = B ⇒ LUX = B
Now A = LU

.png)
Equating, the corresponding elements of I rows, we get
![]()
Equating the corresponding elements of second rows, we get
l21u11 = −6 ⇒ l21 × 10 = − 6 ⇒ l21 = ![]() = −0.6
= −0.6
l21u12 + u22 = 8
⇒ (-0.6) (-7) + u22 = 8 ⇒ u22 = 8 − 4.2 = 3.8
l21u13 + u23 = −1
(-0.6) (3) + u23 = -1 ⇒ u23 = −1 + 1.8 = 0.8
l21u14 + u24 = −4
⇒(−0.6) (5) + u24 = -4 ⇒ u24 = -4 + 3 = −1
Equating the corresponding elements of third rows, we get
l31u11 = l31 = = 0.3
l31u12 l32u22 = 1
= = l32 = = 0.8158
l31u13 l32u23 u33 = 4
= u33 =−− 0.65264 = 2.4474
l31u14 l32u24 u34 = 11
= u34 =− 1.5 + 0.8158 = 10.3158
Equating the corresponding elements of fourth rows, we get
l41u11 = l41 × l41 = ![]() = 0.5
= 0.5
l41u12 l42u22 = −9
∴ l42 −9
= l42 = = −1.4474
l41u13 l42u23 l43u33 = −2
∴ l43 −2
= −2
= −2.3421
l43 = −0.9570
l42u24 l43u34 u44 = 4
= 4

Hence


AX = B ∴ LUX = B
Put UX = Y,  ∴ LY = B
∴ LY = B

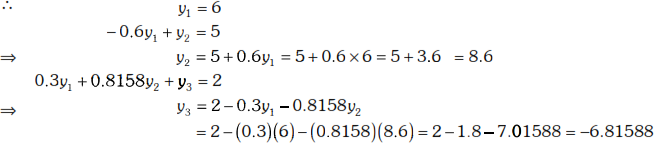
and ![]()

Now ![]()


and
∴ 
∴ 
∴ 
∴ the solution is ![]()
3.4.2 Crout’s Method
Consider the system of equations

Now

∴ the system of equations is AX = B
In Crout’s method we factorise A as A = LU, where L is taken as lower triangular matrix and U is taken as unit upper triangular matrix.
That is  and
and 
![]()
Let UX = Y, so that LY = B, where 
Since L and B are known, Y is known.
Substituting Y in UX = Y, we can find X, since U is known.
Thus, we can find the solution of the given system of equations.
Note:
In Crout’s method to find ![]() and
and ![]() , we equate the corresponding elements of the columns of A and LU respectively.
, we equate the corresponding elements of the columns of A and LU respectively.
That is to find the elements of L and U, we equate the corresponding elements of columns of A and LU.
WORKED EXAMPLES
Example 1
Factorise  by Crout’s method.
by Crout’s method.
Solution
Given 
By Crout’s method, we take A = LU,

Equating elements of I Columns, we get
![]()
Equating elements of II Column, we get

Equating elements of III column, we get
∴
∴
Example 2
Solve the system of equations ![]() using Crout’s method.
using Crout’s method.
Solution
The given system of equations is

Here

∴ the given system is AX = B.
By Crout’s method, we take A = LU,

Equating the corresponding elements of I column, we get
![]()
Equating the corresponding elements of II columns, we get

Equating the corresponding elements of third column, we get


![]()
Put Y = UX, where 
∴ LY = B




∴ 
and ![]()
∴ the solution is ![]()
Example 3
Solve by Crout’s method, the system of equations ![]()
![]() .
.
Solution
The given system of equations is

Here


∴ the given system is AX = B
By Crout’s method, we take A = LU

Equating the corresponding elements of the first columns, we get
![]()
Equating the corresponding elements of the second columns, we get

![]()
Equating the corresponding elements of third columns, we get
∴ 
∴ 

Now![]()
Put UX = Y, where  ∴ LY = B
∴ LY = B
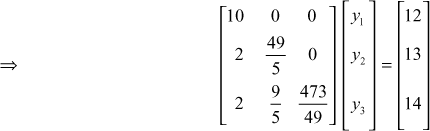




Now
![]()




∴ the solution is ![]()
3.4.3 Cholesky Decomposition
We have seen the triangular factorisation of a square matrix by Doolittle’s method and Crout’s method. Cholesky decomposition is slightly different from the two methods.
Cholesky method is commonly used in signal processing.
In Cholesky method, to factorise the square matrix, the matrix should be symmetric and positive definite.
A symmetric matrix is positive definite if all the principal minors are positive.
That is if

The principal minors are
 and
and 
Definition: Let A be a symmetric matrix and positive definite. Then A can be decomposed as A = LLT, where L is a lower triangular matrix with digonal elements positive.
L and LT are called cholesky factors of A.
Application of Cholesky decomposition to solve the system of linear equations
Consider the system of equations 
Let 
∴ the system of equations is AX = B.
By Cholesky decomposition, let A = LLT
where

![]()
Put ![]() where
where 
![]()
Since L and B are known, Y is known.
![]() gives X.
gives X.
WORKED EXAMPLES
Example 1
Obtain Cholesky factorisation of the matrix  .
.
Solution
Let 
The elements equidistant from the main diagonal are the same and hence A is symmetrix,
The principal minors are

All the principal minors are positive and so A is positive definite.
So, we can use cholesky method to factorize A. We take A = LLT
where
 and
and 
∴ 
Equating the corresponding elements of I columns, we get

Equating the corresponding elements of second columns
![]()
⇒ ![]()
Equating the corresponding elements of third columns, we get
⇒ 
∴ 
∴ 
Example 2
Find Cholesky’s factorisation to the matrix  . Hence solve the equations
. Hence solve the equations ![]() .
.
Solution
Let 
A is symmetric and principal minors are ![]()
and 
![]()
∴ A is symmetric and positive definite:
So, we use cholesky’s method to factorize A. We take A = LLT,
where 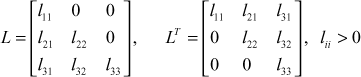
∴ 
Equating the corresponding elements of first columns, we get

Equating the corresponding elements of second columns, we get
![]()
and ![]()
⇒ ![]()
Equating the corresponding elements of third columns, we get
![]()
∴ 
The given system of equations is

The coefficient matrix is 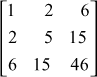
This is same as the given matrix A.
∴ the given system of equations is AX = B, where 
∴ ![]()
Put ![]() where
where 
![]()
⇒ ∴ 
⇒ 
⇒ ![]()
and ![]() = 6
= 6
⇒ ![]()
⇒ ![]()
∴ 
∴ ![]()
⇒ 
⇒ 
⇒ ![]()
∴ ![]()
![]()
∴ the solution is ![]()
Example 3
Obtain the Cholesky decomposition of  and hence solve the system.
and hence solve the system.
AX = b where ![]() and
and ![]() .
.
Solution
Given  and it is symmetric
and it is symmetric
The principal minors are ![]()

∴ A is symmetric and positive definite.
So, we can use Cholesky’s decomposition to factorize A. We take A = LLT
where

∴
Equating Corresponding elements of first columns, we get

Equating corresponding elements of second columns, we get
⇒ 
⇒ ![]()
Equating the corresponding elements of third columns, we get

∴ 
Given AX = b, where ![]() and
and ![]()
Now ![]()
Put ![]() , where
, where  ∴
∴ ![]()
⇒ 
⇒ 
∴ 
and ![]()
![]()
⇒ ![]()
∴ 
Now
![]()
⇒ 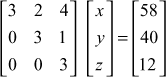
⇒ 
∴ 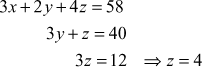
∴ ![]()
![]()
and ![]()
![]()
∴ ![]()
∴ the solution is ![]()
Note: In L, if the diagonal elements are not unity, then also we can factorize the given matrix A.
Example 4
Let  , then find two triangular matrices L (lower triangular) and U (upper triangular) such that A = LU , using the diagonal elements of L as 3, 1, 5. Hence find A –1.
, then find two triangular matrices L (lower triangular) and U (upper triangular) such that A = LU , using the diagonal elements of L as 3, 1, 5. Hence find A –1.
Solution
Given 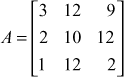
Let A = LU, where  and
and 

Equating the corresponding elements of each row, we get






∴ 
Since ![]() then
then ![]() where
where ![]()
∴ 

Exercises 3.5
- Determine the LU factorisation of the matrix
 by Doolittle’s method.
by Doolittle’s method. - Determine the LU factorisation of the matrix
 by Doolittle’s method.
by Doolittle’s method.
(I) Solve by using Doolittle’s method the following system equations.
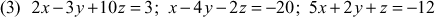



- Find the LU factorisation of the matrix
 by Doolittle’s method and hence solve the system of equations
by Doolittle’s method and hence solve the system of equations  .
. - Given
 , find the LU factorisation of A by Doolittle’s method and hence solve the system of equations AX = B where
, find the LU factorisation of A by Doolittle’s method and hence solve the system of equations AX = B where  .
.
(II) Solve by using Crout’s method the following system of equations.



- Find the inverse of
 using crout’s method.
using crout’s method. - Find the crout’s factorisation of the matrix
 .
.
(III) Solve by using Cholesky’s method



- Find the Cholesky decomposition of the matrix A =
 and hence solve the system AX = B, where
and hence solve the system AX = B, where  and
and  .
. - Find the Cholesky factorisation of the matrix
 and hence solve the system AX = B, where
and hence solve the system AX = B, where  and
and  .
. - Find the Cholesky decomposition for the matrix
 .
.
Answers 3.5
 and
and 
 and
and 
 (4)
(4) 
 (6)
(6) 


 (10)
(10) 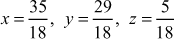


 (14)
(14) 
 (16)
(16) 



Short Answer Questions
- What are direct methods?
- What are indirect methods?
- Give two direct methods to solve a system of linear equations.
- Give two indirect methods to solve a system of linear equations.
- Using Gauss elimination method solve
 .
. - Explain briefly Gauss-Seidel method of solving simultaneous linear equations.
- Solve the linear system
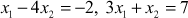 by Gauss-Jordan method.
by Gauss-Jordan method. - What is the condition for convergence of Gauss-Seidel method?
- Why Gauss-Seidel methd is better than Jacobi’s-iterative method?
- Compare Gauss elimination and Gauss-Seidel method?
- If we start with zero values for x, y, z while solving

 by Gauss-Seidel iteration, find the values for x, y, z after one iteration.
by Gauss-Seidel iteration, find the values for x, y, z after one iteration. - Find the inverse of
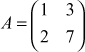 by Gauss-Jordan method.
by Gauss-Jordan method. - Find the first iteration values of x, y, z satisfying
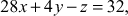
 by Gauss-Seidel method.
by Gauss-Seidel method. - Given
 find the inverse of the coefficient matrix.
find the inverse of the coefficient matrix. - Solve
 by Jordan’s method.
by Jordan’s method. - Write down the sufficient conditions for the solution of the linear system Ax = B by LU method of Doolittle or Crout.
- Write down the sufficient Condition for the solution of the linear system Ax = B by Cholesky’s method.
- Factorize
 by Doolittle’s method.
by Doolittle’s method. - Factorize
 by Crout’s method.
by Crout’s method. - Factorize
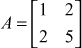 by Choleskey’s method.
by Choleskey’s method. - What is the drawback of Jacobi’s method in finding the eigen values of a symmetric matrix?
- What is the minimum number of rotations required to bring the symmetric matrix A of order n in to diagonal form.
- Determine the largest eigen value and the corresponding eigen vector of the matrix
 correct to two decimal places using power method.
correct to two decimal places using power method. - Write down all possible types of initial vectors to determine the largest eigen value and the corresponding eigen vector of a matrix of size
 .
.
