5.0 INTRODUCTION

In Chapter 4, using interpolation methods, we found the value of the entry y for an intermediate value of the argument x, from a given table of value of x and y.

Sometimes we have to find the value of x for a given values of y not in the table. This reverse process is known as inverse interpolation.

Thus inverse interpolation is defined as the process of finding the value of the argument corresponding to a given value of the function lying between two tabulated functional values.

In this chapter, we use the following methods to find the value of the argument x for a given value of y.

1. Lagrange’s inverse interpolation formula
2. Successive approximation method or iteration method
3. Reversion of series method

5.1 LAGRANGE’S INVERSE INTERPOLATION FORMULA

Whether the arguments are equally spaced or not, the entries are always unequally spaced. So, Lagrange’s formula is the natural choice, because lagrange’s formula is merely a relation between two variables, either of which may be chosen as the independent variable.

Given a set of values treating y as the independent variable and x as the dependent variable we have the inverse form of Lagrange’s formula

WORKED EXAMPLES

Example 1

If

x	2	3	5
Ux	113	286	613

find correct to two decimals the value of x for which U_x = 1001.

Solution

Let y = Ux

Given x₀ = 2, x₁ = 3, x₂ = 5

andy₀ = 113, y₁ = 286, y₂ = 613

Required the value of x when y = 1001

Lagrange’s inverse interpolation formula is

When y = 1001, we get

∴ the value of x correct to 2 places of decimals is 7.56

Example 2

Use Lagrange’s formula inversely to obtain the value of t when A = 85 from the following table.

t	2	5	8	14
A	94.8	87.9	81.3	68.7

Solution

Let us take t = x and A = y

and

Lagrange’s inverse interpolation formula is

When y = 85, we get

∴ when A = 85,

Example 3

Apply Lagrange’s formula inversely to obtain the root of the equation given that and

Solution

Let

The given values of x are x₀ = 30, x₁ = 34, x₂ = 38, x₃ = 42

and the corresponding values of y are y₀ = −30, y₁ = −13, y₂ = 3, y₃ = 18

Required the value of x when y = 0

Lagrange’s inverse interpolation formula is

When y = 0, we get

∴ the root of the equation is x = 37.23

Exercises 5.1

1. Applying Lagrange’s formula inversely find x when given
2. In the following table h denote the height (in feet) above sea level and p, the barometric pressure

   h	0	2753	4763	6942	1053
   p	30	27	27	23	20

   Find the height when the pressure is 32 by Lagrange’s inverse interpolation formula.

3. If f(0) = 16.35, f(5) = 14.88, f(10) = 13.59, f(15) = 12.46, find x when f(x) = 14 by Lagrange’s method.
4. Apply Lagrange’s formula inversely to find the value of x when f(x) = 15 from the given data.

   x	5	6	9	11
   f(x)	12	13	14	16

5. By inverse interpolation formula find x when cosh 1.285 from the given table.

   x	0.736	0.737	0.738	0.739	0.740
   y = cosh x	1.2833	1.2841	1.2849	1.2859	1.2865

Answers 5.1

(1) 2.8 (2) 1691 feet below sea level (3) 8.337 (4) 11.5 (5) 0.73811

5.2 SUCCESSIVE APPROXIMATION METHOD OR ITERATION METHOD

In Lagrange’s inverse interpolation formula each term is important and omission of any term will lead to serious errors. So this method is unsuitable when the number of arguments (and entries) is large as the computations become very tedious.

When the arguments are equally spaced, we have a simpler method based on successive approximation or iteration. It consists in using Newton’s forward interpolation formula or any one of the central difference formulae.

We shall illustrate the method with Newton’s forward difference formula

where

(1)

To find the first approximation for u, we neglect the second and higher order differences.

To find the second approximation, put u = u₁ on the R.H.S of (1)

To find the third approximation put u = u₂ in the R.H.S of (1)

This process is repeated till two successive approximations coincide up to the desired degree of accuracy.

WORKED EXAMPLES

Example 1

Find x when y = 0.2 from the following table:

Solution

From the given table of values of x and y, we find that value of y = 0.2 occurs for a value of x lying between 0.3 and 0.4

So, we choose the origin as x₀ = 0.3. Here h = 0.1

We form the difference table.

Applying Newton’s formula, we get

∴

∴

When y = 0.2, we get

∴

(1)

First approximation value of u is

u₁ = 0.3158

Substituting in the R.H.S of (1), the second approximation is

u₂ = 0.3158 + 0.0263 u₁(u₁−1) − 0.00877 u₁(u₁−1)(u₁−2)

u₂ = 0.3158 + 0.0263 (0.3158) (0.3158 − 1)

− 0.00877 (0.3158) (0.3158 − 1) (0.3158 − 2)

= 0.3158 − 0.00568 − 0.00319 = 0.3069

Third approximation is

u₃ = 0.3158 + 0.0263 u₂(u₂ − 1) − 0.00877 u₂(u₂ − 1) (u₂ − 2)

∴ u₃ = 0.3158 + 0.0263 (0.3069) (0.3069 − 1)

− 0.00877 (0.3069) (0.3069 − 1) (0.3069 − 2)

= 0.3158 − 0.00559 − 0.003158 = 0.3070

Fourth approximation is

u₄ = 0.3158 + 0.0263 u₃(u₃ − 1) − 0.00877 u₃ (u₃ − 1) (u₃ − 2)

= 0.3158 + 0.0263 (0.3070) (0.3070 − 1)

− 0.00877 (0.0370) (0.3070 − 1)(0.3070 −2)

= 0.3158 + 0.005596 − 0.003159 = 0.3070

Since u₃ and u₄ are same for 3 places; we take u = 0.3070

∴

∴ x − 0.3 = 0.3070 × 0.1 = 0.03070

∴ x = 0.3 + 0.0307 = 0.3307

Example 2

Solve the equation given the following data.

x	1.35	1.36	1.37	1.38
	0.1303	0.1335	0.1367	0.1399

Solution

Given

∴

Let

Hence the given table becomes

x	1.35	1.36	1.37	1.38
y	0.047	0.025	0.003	−0.019

It can be seen from the table that the value y = 0 corresponds to a value of x between 1.37 and 1.38

So we take the origin as and apply Newton’s backward formula.

∴

where

Here

and

∴

We form the difference table.

∴ y = −0.019 + v(−0.022)

When y = 0, we get

0 = −0.019 −0.022v

∴ 0.022v = −0.019

∴

∴

∴ x − 1.38 = −0.8636 × 0.01

∴ x = 1.38 − 0.008636 = 1.371364.

∴ the root correct to four decimal places is x = 1.3714

Example 3

Determine the positive root of by inverse interpolation.

Solution

Let

We find

= 64 + 16 + 4 − 100 = −16 < 0

So, the root is between 4 and 4.5

We take the values of x as 4, 4.1, 4.2, 4.3, 4.4

We shall form the table as below with y = f(x)

x	4	4.1	4.2	4.3	4.4
y = f(x)	−16	−10.169	−4.072	2.297	8.944

It can be seen that the root lies between 4.2 and 4.3

We shall take the origin as and use Stirling’s formula to find the root.

Stirling’s formula is

where

We shall form the difference table.

∴

When y = 0, we get

0 = −4.072 + 6.233 u + 0.136 u² + 0.001 u (u² − 1)

∴ 6.233 u = 4.072 − 0.136 u²− 0.001 u (u² − 1)

∴

∴

First approximation is

Second approximation is

Third approximation is

Fourth approximation is

Since u₃ and u₄ coincide upto 4 decimal places, u = 0.6442

∴

∴ the root correct to four decimal places is

Example 4

Find the value of x if given the following table.

x	50	52	54	56
	3.684	3.732	3.779	3.825

Solution

Let

Required the value of x if That is to find x when y = 3.756

From the given table, it is obvious that 3.756 lies between x = 52 and x = 54.

So, we choose the origin as and use Stirling’s formula to find the value of x.

Stirling’s formula is

where

We shall form the difference table

∴

= 3.732 + 0.0475 u −0.0005u²

∴ 0.0475 u = y − 3.732 + 0.0005u²

When y = 3.756, we get

0.0475u = 3.756 − 3.732 + 0.0005u²

= 0.024 + 0.0005u²

∴

= 0.5053 + 0.01053 u²

First approximation is

Second approximation is

= 0.5053 + 0.01053 (0.5053)²

= 0.5053 + 0.002689

= 0.5080

Third approximation is

= 0.5053 + 0.01053 (0.5080)²

= 0.5053 + 0.0027174

= 0.5080

Since u₂ and u₃ coincide upto four decimal places,

∴

∴ x − 52 = 0.5080 × 2

∴ x = 52 + 1.0160 = 53.0160 = 53

∴ if , then the value of

Exercises 5.2

1. Find the solution of the equation x² − 6x − 11 = 0 between 3 and 4, by iteration.
2. Given the following table of values of probability integral find the value of x for which the integral is equal to by iteration.

   x	0.45	0.46	0.47	0.48	0.49	0.50
   I(x)	0.475	0.484	0.493	0.502	0.511	0.520

3. The following table gives the values of sinh x for certain equidistance values if x.

   x	4.80	4.81	4.82	4.83	4.84
   sinh x	60.7511	61.3617	61.9785	62.6015	63.2307

   Find the value of x when sinh x = 62.

4. Find the real root of the equation x³ + x - 5 = 0, correct to two places of decimals.
5. Find the real root of the equation x³ - 2x - 5 = 0, correct to two places of decimals.
6. Find the positive root of the equation x³ - 5x + 3 = 0.

Answers 5.2

1. 3.091 (2) 0.4769 (3) 4.8203 (4) 1.52 (5) 2.09 (6) 0.6566

5.3 REVERSION OF SERIES METHOD

All the interpolation formula we have seen so far are expressed as a series containing powers of u, where

In other words, they are all power series in u of the form

where are known constants

We know that any convergent power series can be reverted.

Now

Put then

where

We shall express u as a power series in v.

Let

Substituting for v, we get

∴

Equating like coefficients of u on both sides, we get c₀ = 0, c₁ = 1,

∴

∴

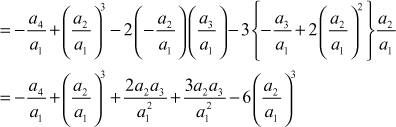
∴ and so on.

Hence

where v is known, once f(u) is known.

WORKED EXAMPLES

Example 1

Using the method of reversion of series of Newton’s formula of interpolation find x, for y = 3000 from the following data.

x	10	15	20
y = f(x)	1754	2648	3564

Solution

We have to use Newton’s formula to find x when y = 3000

Choose the origin as Here h = 5

∴

We form the difference table.

Newton’s formula is

∴

Now

Given y = 3000

Now

where

∴

= 1.3862

∴ when y = 3000,

Example 2

The equation x² - 6x - 11 = 0 has a root between 3 and 4 obtain it by inverse interpolation.

Solution

Let

Since the root lies between 3 and 4, we form a table and use reversely.

The table is

x	2.8	2.9	3	3.1	3.2	3.3
y	−5.848	−4.011	−2	0.191	2.568	5.137

The value of y = 0 for a value of x between 3 and 3.1 and it is closer to 3.1.

We choose the origin as Here h = 0.1

∴

We form the difference table.

We shall apply Newton’s forward formula and find the value of x when y = 0

Newton’s forward formula is

Here

Since y = 0,

Now

where

∴

∴

∴ the root of the equation is

Example 3

From the data given below, determine correct to four decimals the value of x for which f(x) is equal to 0.5.

x	0.45	0.46	0.47	0.48	0.49	0.5
f(x)	0.47548	0.48466	0.49375	0.50275	0.51167	0.5205

Solution

Let y = f(x)

From the given table, we observe that when the value of x is between 0.47 and 0.48 and is nearer to 0.48

∴ choose the origin as Here h = 0.01

∴

We use Stirling’s formula to find x when

Stirling formula is

We form the difference table.

∴

= 0.50275 + 0.00896u −0.00003917u² −0.0000008333u⁴

∴ a₀ = 0.50275, a₁ = 0.00896, a₂ = −0.00003917, a₃ = 0,

a₄ = −0.0000008333.

Given

∴

Now

where

∴

and

= 0.00009297 − 0.000000417 = 0.00009255

∴

∴ u = −0.3069 + 0.00437(−0.3069)²

+ 0.0003819 (−0.3069)³ + 0.00009255(−0.3069)⁴ = − 0.306499

∴

∴ x = 0.48 + 0.01 (−0.306499)

= 0.48 − 0.00306499

= 0.48 − 0.00306 = 0.4769 to four places.

∴ when

Exercises 5.3

1. Estimate the value of x when f(x) = 2, given the following table:

   x	4.80	4.81	4.82	4.83	4.84
   f(x)	0.7511	1.3617	1.9785	2.6015	3.2307

2. Find x when ux = 0.163, given

   x	80	82	84	86	88
   ux	0.134	0.154	0.176	0.200	0.227

3. Using inverse interpolation find the root of which lies between 2 and 3.

Answers 5.3

1. 4.8202
2. 82.8
3. 2.42599

Short Answer Questions

1. What is inverse interpolation?
2. Write the Lagrange’s inverse interpolation formula for a set of n observations .
3. Write the Lagrange’s inverse interpolation formula to find x if are given.
4. Find the value of x when y = 1.5 from the following data.

   x	0	1	2
   y	2	0	1

5. Find x when y = 5, from the following data.

   x	1	2	3
   y	1	8	27

6. Using Lagrange’s inverse interpolation formula find x when y = 10 from the following data.

   x	12	13
   y	5	6

7. Given find the value of x when y = 5 by using Lagrange’s formula inversely.