8
Curve Fitting
8.0 INTRODUCTION
Quite often in engineering and science, we conduct experiments involving two quantities, say x and y. Suppose x1, x2, ...,xn be the values of x corresponding to which the values of y are y1, y2 ..., yn. We would like to know the functional relation between x and y. As a first step we plot the points (x1, y1), (x2, y2), .... (xn, yn) with respect to rectangular axes. The resulting set of points plotted is called a scatter diagram. From the scatter diagram it is possible to visualize a smooth curve which passes as closely as possible to these points and that approximates the data. Such a curve is called an approximating curve.
The equation of this curve between x and y is called an empirical relation.
For example, in the scatter diagram if the points cluster around a straight line, then we say that a linear relationship exists between x and y. If the points cluster around a curve, then we say a non–linear relationship exists between x and y.
The general problem of finding the equation of the approximating curve that fits the given set of data is called curve fitting.

If the relation is linear, then we assume the empirical relation of the approximating curve as y = ax + b.
The best values of the constants occurring in the equation can be found in different ways. We shall fit a curve by the following methods:
- method of least squares
- method of averages
- method of the sum of exponentials
- method of moments
8.1 METHOD OF LEAST SQUARES
Let (x1, y1), (x2, y2), ..., (xn, yn) be a set of observed data and let y = f (x) be the relation suggested by the scatter diagram.
Let Pi be the point (xi, yi), i = 1,2, 3, ..., n
When x = xi, the observed value is yi and the expected value is f (xi).
Let di = yi – f (xi) be the difference between the observed and expected values for each i.
The differences d1, d2, ..., dn are called the residuals, which may be positive or negative
![]()
The principle of least squares is that the sum of the squares of the residuals is minimum.
It is also referred as Gauss’s least square principle.
The curve fitted by this principle is called the least square curve.

The curve for which![]() is minimum is called a best fitting curve besides all the curves approximating the given set of points.
is minimum is called a best fitting curve besides all the curves approximating the given set of points.
A line fitted by this principle is known as least-square line and a parabola fitted by this principle is known as least square parabola.
Note: The method of least squares gives unique values for the constants and so the curve fitted is unique.
8.1.1 Fit a Straight Line by the Method of Least Squares
Let (x1, y1), (x2, y2) ... (xn, yn) be a set of observed values of the variables x and y.
Let the relation between x and y be y = ax + b(1)
Then, the sum of squares of residuals is
⇒ ![]()
By principle of least squares E is minimum.
Since xi and yi are known, E is a function of a and b.
The conditions for E to be minimum are ![]() and
and ![]()
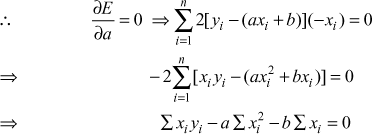
and
![]() (2)
(2)

![]() (3)
(3)
Solving (2) and (3), we get the values of a and b.
For these values of a and b, the line y = ax + b is the best fitted line to the data.
The equations (2) and (3) are called the normal equations for the least–squares line
y = ax + b
Note:
- The formulae can be remembered by omitting the suffixes:
The line is y = ax + b (1)
The normal equations are Σy = aΣx + nb
and Σxy = aΣx2 + bΣx
- If the values of x are equally spaced with interval h, we can simplify the computation by changing the origin and scale by the transformation
 so that
so that 
WORKED EXAMPLES
Example 1
Use the method of least squares to fit a straight line to the following data:
| x | 0 | 5 | 10 | 15 | 20 |
| y | 7 | 11 | 16 | 20 | 26 |
Estimate the value of y when x = 25.
Solution
We fit a straight line to the given data by the method of least squares.
Since the values of x are equally spaced, let ![]()
Then the equation of the line of best fit is
y = aX + b (1)
Normal equations are ![]() (2)
(2)
and ![]() (3)
(3)
To find ![]() we form the table
we form the table
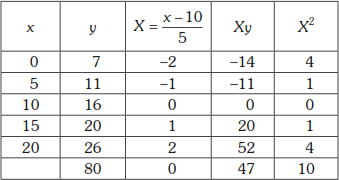
From the table ![]()
![]()
Substituting in (2), we get 80 = a.0 + 5b ⇒ ![]()
Substituting in (3), we get 47 = a.10 + b.0 ⇒ ![]()
⇒ the equation of the line of best fit is


When x = 25, y = 0.94(25) + 6.6 = 30.1
Example 2
In a tensile test of a metal bar the following observation were made where x represents load in tons and y elongation in ten thousands of an inch.
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
|
y |
14 |
27 |
41 |
56 |
68 |
75 |
Using the principle of least squares, find a law of the form y = ax + b.
Solution
We fit a straight line by the principle of least squares.
Here the values of x are equally spaced with h = 1, but n = 6.
So, we choose the origin as the average of the two middle values 3 and 4 and it is ![]()
Let X = x – 3.5
Then, the equation of the line of best fit is y = aX + b
The normal equations are ![]() (2)
(2)
and ![]() (3)
(3)

![]()
Substituting in (2), we get, ![]()
Substituting in (3), we get, ![]()
![]()
⇒ the equations of the line of best fit is

Example 3
Using 1964 as the origin obtain a straight line trend equation by the method of least squares.
|
Year |
1960 |
1962 |
1963 |
1964 |
1965 |
1966 |
1969 |
|
Value |
140 |
144 |
160 |
152 |
168 |
176 |
180 |
Find the trend value of the missing year 1961.
Solution
Let the year be denoted by x, and let the value be denoted by y
Let
X = x – 1964
Then, the equation of the straight line of best fit is
y = aX + b(1)
![]() the normal equations are
the normal equations are ![]() (2)
(2)
and
![]() (3)
(3)

![]()
⇒ The normal equations are
1120 = a.1 + 7b
⇒ 1120 = a + 7b (4)
and
412 = a × 51 + b.1
⇒ 412 = 51a + b(5)
(4) – 7 × (5) ⇒ 1120 – 2884 = a (1 – 357)
⇒ 356 a = 1764
⇒ a = ![]() = 4.955 = 4.96
= 4.955 = 4.96
Substituting in (4), we get
7b + 4.96 = 1120
⇒ 7b = 1120 – 4.96 = 1115.04
⇒ b = ![]()
The straight line trend is y = 4.96X + 159.29
⇒ y = 4.96(x – 1964) + 159.24
When x = 1961,
y = 4.96 (1961 – 1964) + 159.29
⇒ y = 4.96(–3) + 159.29
⇒ y = –14.88 + 159.29 = 144.41
∴ the trend value for the year 1961 is 144.41.
8.1.1 (a) Fitting Other Type of Equations Reducible to the Form 
Certain types of equations can be reduced to the linear form by transformation of variables.
This process is usually called rectification.
Some of such equations are given below.


WORKED EXAMPLES
Example 4
An experiment on the life of a cutting tool at different cutting speeds gave the values given below.
|
Speed vft/min |
350 |
400 |
500 |
600 |
|
Life Tin min. |
61 |
26 |
7 |
2.6 |
It is known that v and T satisfy the relationship v = aT b. Using the method of least squares find the best values of a and b.
Solution
Given v = a Tb
Taking log to the base 10
log10 v = log10 a + b log10 T
Put Y = log10 v, A = log10 a, X = log10 T
Then, the equation is Y = A + bX (1)
which is linear in x and y.
The normal equations are
![]() (2)
(2)
![]() (3)
(3)
We form the table

Substituting in (2) and (3), we get

Example 5
The voltage v across a capacitor at time t seconds is given by the following table. Use the principle of least squares to fit a curve of the form v = aekt to the data.
| t | 0 | 2 | 4 | 6 | 8 |
| v | 150 | 63 | 28 | 12 | 5.6 |
Solution
Given v= aekt.
Taking log to base 10, we get
logl0v= log10 a + kt log10 e
Put Y= log10 v, A = log10 a, B = klog10e, ![]()
∴ the equation is Y= A + BX (1)
By method of least squares, the normal equations are
![]() (2)
(2)
and
![]() (3)
(3)
We form the table

![]()
Substituting in (1), we get 7.2499 = 5A + B.0
![]()
Substituting in (3), we get
–3.5759 = A.0 + B.10
![]()
![]()
A = 1.45 ⇒ log10 a = 1.45 ⇒ a = 101.45 = 28.184
B = –0.3576
⇒ k log10 e = –0.3576
![]()
= −0.3576 loge10
= −0.3576(2.30258) = −0.8234
∴ v = 28.184 e–0.8234t
8.1.1 (b) Fit a Parabola y = ax2 + bx + c by the Method of Least Squares
Let (![]() ), (
), (![]() ), … (
), … (![]() ) be n observed values of x and y.
) be n observed values of x and y.
We have to fit the parabola y = ax2 + bx + c (1)
to this data
The sum of the squares of the residuals is
![]()
Since xi and yi. are known, E is a function of a, b, c.
By principle of least squares E is minimum.
![]() the conditions are
the conditions are ![]()
![]()

![]()
![]() (2)
(2)
Similarly, ![]() (3)
(3)
and ![]() (4)
(4)
Solving (2), (3) and (4) we get the values of a, b, c for which the curve y = ax2 + bx + c is the best fitted curve to the data.
Note: Dropping the suffixes, for simplicity, the normal equations of the least square curve
y = ax2 + bx + c(1)
are Σy = aΣx2 + bΣx + nc(2)
Σxy = aΣx3 + bΣx2 + cΣx(3)
Σx2y = aΣx4 + bΣx3 + cΣx2(4)
They can be remembered as below
Taking Σ of (1) we get (2)
Multiply (1) by x and then taking Σ, we get (3)
Multiplying (1) by x2 and then taking Σ, we get (4).
WORKED EXAMPLES
Example 1
Fit a parabola of the form y = ax2 + bx + c to the following data:
| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 1.8 | 1.3 | 2.5 | 6.3 |
Solution
We fit a parabola to the given data by the method of least square.
The values of x are equally spaced with h = 1
For simplicity in computation we take origin for x.
Put
X = x − 2.
Then the equation of the curve of best fit is
y = aX2 + bX + c (1)
The normal equations are
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
We form the table


Substituting in (2), we get 12.9 = 10a + b.0+5c
![]() 10a + 5c = 12.9
10a + 5c = 12.9
![]() 2a + c = 2.58 (5)
2a + c = 2.58 (5)
Substituting in (3), 11.3 = a.0 + b(10) + c.0
![]() 10 b = 11.3
10 b = 11.3 ![]() b = 1.13
b = 1.13
Substituting in (4), 33.5 = a.34 + b.0 + c.10
![]() 34a + 10c = 33.5
34a + 10c = 33.5
Dividing by 10, 3.4a + c = 3.35 (6)
(6) – (5) ![]() 1.4a = 0.77
1.4a = 0.77
![]()
![]()
Substituting in (5), we get c = 2.58 − 2(0.55) = 2.58 – 1.10 = 1.48
The curve of best fit is y = 0.55X2 + 1.13X + 1.48, where X = x – 2
Example 2
The following table gives the levels of prices in certain years. Fit a second degree parabola to the data:
|
Year |
1975 |
1976 |
1977 |
1978 |
1979 |
1980 |
1981 |
1982 |
1983 |
1984 |
1985 |
|
Price |
88 |
87 |
81 |
78 |
74 |
79 |
85 |
84 |
90 |
92 |
100 |
Solution
We fit a parabola, to the given data by the method of least squares.
Let x denote year and y denote price.
For year, take the origin as 1980. Let X = x – 1980.
Then the equation of the best fitted curve is
y = aX2 + bX + c (1)
The normal equations are
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
we form the table

n = 11, ![]() y = 938,
y = 938, ![]() X = 0,
X = 0, ![]() X2 = 110,
X2 = 110, ![]() X3 = 0,
X3 = 0, ![]() X4 = 1958,
X4 = 1958, ![]() Xy = 130,
Xy = 130, ![]() X2y = 9910
X2y = 9910
Substituting in (3) we get, 130 = a.0 + b.110 + c.0 ![]()
Substituting in (2), we get 938 = a × 110 + b.0 + 11 × c
![]() 110a + 11c = 938
110a + 11c = 938
![]() 10a + c = 85.2727(5)
10a + c = 85.2727(5)
Substituting in (4), 9910 = 1958a + 0.b + 110c
![]() 1958a + 110 c = 9910
1958a + 110 c = 9910
Dividing by 110, 17.8a + c = 90.0909(6)
(6) – (5) ![]() 7.8a = 4.8182
7.8a = 4.8182

Thus a = 0.62, b = 1.18, c = 79.10
The curve of best fit is ![]() where X = x – 1880
where X = x – 1880
Example 3
Fit a second degree parabola of the form y = ax2+ bx+ cto the following data taking xas the independent variable.
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
y |
2 |
6 |
7 |
8 |
10 |
11 |
11 |
10 |
9 |
and introducing the new variable uand vby the equations u = x - 5, v = y - 7.
Solution
We fit a parabola to the given data by the method of least squares.
Since the given new variables are u and v and u = x – 5,v = y – 7, taking u as the independent variable, and v as the dependent variable the equation of the parabola in u and v is
v = au2 + bu + c (1)
The normal equations are
 (2)
(2)

n = 9, ![]() u = 0,
u = 0, ![]() u2 = 60,
u2 = 60, ![]() u3 = 0,
u3 = 0,
![]() u4 = 708,
u4 = 708, ![]() v = 11,
v = 11, ![]() uv = 51,
uv = 51, ![]() u2v = −9
u2v = −9
Substituting in (2), (3) and (4), we get
11 = a × 60 + b × 0 + 9c
![]() 60a + 9c = 11
60a + 9c = 11
![]()
![]() 6.6667a + c = 1.2222 (5)
6.6667a + c = 1.2222 (5)
51 = a.0 + b.60 + c.0
![]() 60b = 51
60b = 51 ![]() b =
b = ![]() = 0.85 (6)
= 0.85 (6)
and – 9 = a × 708 + b.0 + c × 60
![]() 708a + 60c = − 9
708a + 60c = − 9
![]()
![]() a + c =
a + c =![]()
![]() 11.8a + c =
11.8a + c = ![]() 0.15 (7)
0.15 (7)
(7) − (5) ![]() 5.1333a =
5.1333a = ![]() 1.3722
1.3722 ![]()
![]()
(5) ![]() c = 1.2222 − 6.6667 × (–0.2673)
c = 1.2222 − 6.6667 × (–0.2673)
= 1.222 + 1.7820 = 3.0042
![]() a = −0.2673, b = 0.85, c = 3.0042
a = −0.2673, b = 0.85, c = 3.0042
![]() v = –0.2673 u2 + 0.85u + 3.0042
v = –0.2673 u2 + 0.85u + 3.0042
![]() y – 7 = −0.2673 (x – 5)2 + 0.85 (x – 5 ) + 3.0042
y – 7 = −0.2673 (x – 5)2 + 0.85 (x – 5 ) + 3.0042
![]() y = 7 – 0.2673 (x2 – 10x + 25) + 0.85x – 4.25) + 3.0042
y = 7 – 0.2673 (x2 – 10x + 25) + 0.85x – 4.25) + 3.0042
![]() y = – 0.2673x2 + 3.523x – 0.9283
y = – 0.2673x2 + 3.523x – 0.9283
Example 4
Fit a parabola of the form y = ax2+ bx+ cto the following data by the method of least squares and predict the value of ywhen x = 70.
|
X |
71 |
68 |
73 |
69 |
67 |
65 |
66 |
67 |
|
Y |
69 |
72 |
70 |
70 |
68 |
67 |
68 |
64 |
Solution
We have to fit a parabola of the form y = ax2 + bx + c by the method of least squares.
Let X = x – 67, Y = y –70
![]() the equation is Y = aX2 + bX + c (1)
the equation is Y = aX2 + bX + c (1)
The normal equations are

we form the table

n = 10, ![]() X = 10,
X = 10, ![]() ,
, ![]() X3 = 280,
X3 = 280,
![]() X4 = 1586,
X4 = 1586, ![]() XY = 6,
XY = 6, ![]() X2Y = –28
X2Y = –28
Substituting in (2), (3) and (4), we get
–12 = a × b2 + b × 10 + 8c
![]() 7.75a + 1.25b + c = –1.5(5) [Dividing by 8]
7.75a + 1.25b + c = –1.5(5) [Dividing by 8]
6 = a × 280 + b × 62 + c × 10
![]() 28a + 6.2b + c = 0.6 (6) [Dividing by 10]
28a + 6.2b + c = 0.6 (6) [Dividing by 10]
and –28 = a × 1586 + b × 280 + c × 62
![]() 25.58a + 4.52b + c = –0.45 (7) [Dividing by 62]
25.58a + 4.52b + c = –0.45 (7) [Dividing by 62]
(6) − (5) ![]() 20.25a + 4.5b = 2.1
20.25a + 4.5b = 2.1
![]() 4.09 a + b = 0.4242 (8)
4.09 a + b = 0.4242 (8)
(6) – (7) ![]() 2.42a + 1.68b = 0.15
2.42a + 1.68b = 0.15
![]() 1.44 a + b = 0.089 (9)
1.44 a + b = 0.089 (9)
(8) – (9) ![]() 2.65a = 0.3352
2.65a = 0.3352 ![]()
![]()
(9) ![]() b = 0.089 – 1.44 × 0.1265
b = 0.089 – 1.44 × 0.1265
= 0.089 – 0.182 = –0.093
c = 0.6 – 28 × 0.1265 – 6.2 (–0.093)
= 0.6 – 3.542 + 0.5766 = –2.3654
∴ The equation of the parabola is
Y = 0.1265 X2 – 0.093X – 2.3654
![]() y – 70 = 0.1265 (x – 67 )2 − 0.093(x – 67) – 2.3654
y – 70 = 0.1265 (x – 67 )2 − 0.093(x – 67) – 2.3654
![]() y = 0.1265x2 – (0.093 + 16.95)x
y = 0.1265x2 – (0.093 + 16.95)x
+ 567.8585 + 6.231 – 2.3654 + 70
![]() y = 0.1265x2 – 17.043 x + 641.724
y = 0.1265x2 – 17.043 x + 641.724
When x = 70, y = 0.1265 × 702 – 17.043 × 70 + 641.724
![]() y = 619.85 – 1193.01 + 641.724 = 68.564 = 69
y = 619.85 – 1193.01 + 641.724 = 68.564 = 69
Exercises 8.1
By method of least squares fit the indicated curve to the given data:
Fit a straight line to the data:
|
x |
0 |
1 |
2 |
3 |
4 |
|
y |
1 |
1.8 |
3.3 |
4.5 |
6.3 |
Fit a straight line to the data:
|
x |
75 |
80 |
93 |
65 |
87 |
71 |
98 |
68 |
84 |
77 |
|
y |
82 |
78 |
86 |
72 |
91 |
80 |
95 |
72 |
89 |
74 |
(3) Find the least square line for the data below:
|
x |
1 |
2 |
4 |
6 |
8 |
9 |
11 |
14 |
|
y |
1 |
2 |
4 |
4 |
5 |
7 |
8 |
9 |
smoothen the data in the above by using the least square line.
(4) The weights of calf taken at weekly intervals are supplied below. Fit a straight line and calculate the average rate of growth per week.
|
Age x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Weight y |
52.5 |
58.7 |
65.0 |
70.2 |
75.4 |
81.1 |
87.2 |
95.5 |
102.2 |
106.4 |
(5) Fit a curve of the form y = ax + bx2 to the data:
|
x |
1 |
2 |
3 |
4 |
5 |
|
y |
1.8 |
5.1 |
8.9 |
14.1 |
19.8 |
Calculate y when x = 2.
![]()
(6) Given
|
x |
2 |
4 |
6 |
8 |
|
y |
5.5 |
14.5 |
26.2 |
41.8 |
Fit a law of the form y = ax + bx2 by computing the least square line.
![]()
(7) For the law of the ![]() + bx, find the best values of a and b from the following data
+ bx, find the best values of a and b from the following data
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
|
y |
5.4 |
6.3 |
8.2 |
10.2 |
12.6 |
15 |
(8) Fit an equation of the form y = aebx for the data
|
x |
1 |
2 |
3 |
4 |
|
y |
1.65 |
2.70 |
4.50 |
7.35 |
(9) The pressure and volume of a gas are known to be related by the equation pv = c, a constant. In an experiment, the following volumes of quantity of gas were observed for the pressures specified. Fit the same equation taking P as independent variable.
|
P (kg/sq.cm) |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
3.0 |
|
v (litres) |
1.62 |
1.00 |
0.75 |
0.62 |
0.52 |
0.46 |
Growth of bacteria (y) in a culture after x hours is given in the following table. Fit a curve of the form y = abx by method of least squares.
|
House x |
0 | 1 | 2 | 3 | 4 | 5 | 6 |
|
No. of bacteria y |
32 | 47 | 65 | 92 | 132 | 190 | 275 |
Estimate y when x = 7.
Find the least squares parabola for the data:
| x | 0 | 2 | 4 | 6 | 8 | 10 |
| y | 1 | 3 | 13 | 31 | 57 | 91 |
Find the least square parabola to the data:
|
x |
0 |
1 |
2 |
3 |
4 |
|
y |
1 |
5 |
10 |
22 |
38 |
Answers 8.1
(1) y = 1.33x + 0.72, (2) y = 0.66x + 29.13
(3) The least square line is y = 0.62x + 0.75
The estimated values of y obtained from this line corresponding to x = 1,2, … 9,11,14 are the smoothening values. The smoothened values of y are 1.37, 1.99, 3.23, 4.47, 5.71, 633, 7.57, 9.43
(4) y = 6.16 x + 45.74, rate of growth = 6.16 (5) When x = 2, y = 486
(6) Y = 1.95 + 0.41x and y = 1.95x + 0.41x2 (7) a = 2.7907, b = 2.413
(8) y = e0.4994x (9) Pv0.422 = 0.9972
(10) y = 32.15 (1.427)x ; when x = 7, y = 387 (11) y = x2 – x + 1
(12) y = 2.2x2 + 0.3x + 1.4
8.2 METHOD OF GROUP AVERAGES
Let (x1, y1). (x2, y2), (x3, y3), … (xn,yn) be the set of observed values of the related variables x and y.
Let y = a + bx (1)
be the assumed linear relationship between the two variables.
To determine the constants a and b, we need two equations in a and b.

When x = x1, the observed value of y is y1 and the estimated values of y from (1) is a + bx1
Their difference is called residual or deviation.
Thus d1= y1– (a + bx1) is the residual for the point (x1, y1).
Similarly for the other points we find the residuals
d2 = y2 – (a + bx2), d3 = y3 – (a + bx3), … dn = yn – (a + bxn)
Some of the residuals may be positive, some of them may be negative or zero. The method of group averages is based on the assumption that the sum of the residuals is zero. ie. ![]()
Since we require two equations in a and b to find out the values of a and b, we divide the given data into two groups such that the sum of residuals is zero for each group.
Let the first group contain r observations, say, (x1, y1), (x2, y2), (x3, y3), … (xr,yr) and the second group contain remaining (n – r) observations.


Dividing by r, we get

![]()
![]() (2)
(2)
where


Similarly

![]()


Dividing by (n – r),

![]()
where

Solving (2) and (3), we get a and b.
Substituting the values of a and b in (1), we get the line fitted to the data.
Note:
- (1) Since
 and
and  are the average values of x and y in the first group and
are the average values of x and y in the first group and  ,
,  are the average values of x and y in the second group, the method is known as method of averages.
are the average values of x and y in the second group, the method is known as method of averages. - If we divide the data into two groups in a different way such that the sum of the residuals is zero in each group, then the values of a and b will be different, and so the equation will be different. This is the serious draw back of this method.
- Since y = a + bx is satisfied by (
 ) and (
) and ( ), this line is the line joining the points (
), this line is the line joining the points ( ) and (
) and ( ). So the equation of the line fitted to the data is
). So the equation of the line fitted to the data is 
- (4) In practice, we divide the data into two groups which contain the same number of points.
WORKED EXAMPLES
Example 1
Fit a straight line of the form y = a + bx by the method of group averages for the following data:
|
x |
0 |
5 |
10 |
15 |
20 |
25 |
|
y |
12 |
15 |
17 |
22 |
24 |
30 |
Solution
Given 6 sets of values, we divide it into two groups each containing 3 sets of values.

∴ 

∴ the equation of the line fitted to the data is

Example 2
The weights of a calf taken at weekly intervals are given below. Fit a straight line by method of averages.
|
Age in weeks |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Weight |
52.5 |
58.7 |
65 |
70.2 |
75.4 |
81.1 |
87.2 |
95.5 |
102.2 |
108.4 |
Calculate also the average rate of growth per week.
Solution
Let x denote the age in weeks and y denote the corresponding weight.
We divide the given data of 10 values into two groups of 5 values each.


Equation of the straight line fitted to data is
![]()

The rate of growth is ![]()
Example 3
Experimental values of two connected quantities x, yare given below:
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
|
y |
2.6 |
5.4 |
8.7 |
12.1 |
16 |
20.2 |
If the relation between x and y is y = ax + bx2 where a and b are constants, find the best values of a and b.
Solution
The given equation is y = ax + bx2
⇒ y = x (a + bx)
⇒ ![]()
Put ![]() and X = x. Then the equation is Y = a + bX, which is linear in X and Y.
and X = x. Then the equation is Y = a + bX, which is linear in X and Y.
Divide the given set of 6 values into two groups of 3 values each.


∴ the linear equation in X and Y is
![]()
⇒ ![]()

Example 4
The data in the following table fit a formula of the type y = axn. Find the values of aand nand the formula by the method of group averages.
|
x |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
|
y |
1.06 |
1.33 |
1.52 |
1.68 |
1.81 |
1.91 |
2.01 |
2.11 |
Solution
Given y = axn
Taking log to the base 10,
log10 y = log10 a + n log10 x
Put Y = log10 y, X = log10 x and A = log10 a
∴ the equation is Y = A + nX, which is linear in X and Y.
Divide the given data into two groups of 4 values each.



∴ the equation in X and Y is
![]()


Example 5
Fit a curve of the form ![]() to the following data by the method of averages.
to the following data by the method of averages.
|
x |
8 |
10 |
15 |
20 |
30 |
40 |
|
y |
13 |
14 |
15.4 |
16.3 |
17.2 |
17.8 |
Hence find the values of a and b.
Solution
Given ![]()
![]()
Put ![]()
∴ the equation is Y = aX + b, which is linear in x and y.
Divide the given data into two groups of 3 values each.
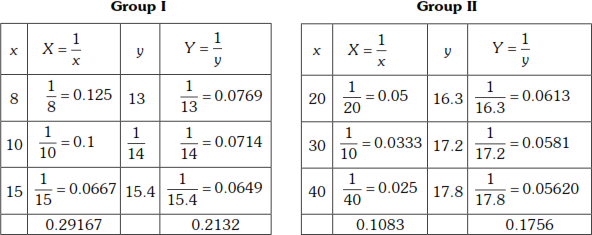

∴the equation in X and Y is ![]()

Type 2. Equations of the form y = a + bx + cx2
We reduce this equation to the above type and solve.
Let (x1,y1) be a particular point on y = a + bx + cx2 satisfying the equation.
Then, y1 = a + bx1 + cx12
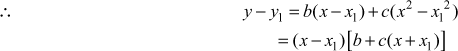

Then, we get Y = b + cX, which is linear in X and Y.
We use group average method to find b and c.
Example 6
The data given below will fit a formula of the type y = a + bx + cx2. Find the formula.
| x |
87.5 |
84.0 |
77.8 |
63.7 |
46.7 |
36.9 |
| y | 292 | 283 | 270 | 235 | 197 | 181 |
Solution
Given y = a + bx + cx2(1)
Taking (87.5, 292) as a particular point on (1), we get
292 = a + b(87.5) + c(87.5)2(2)
(1) − (2)⇒ y – 292 = b[x – 87.5] + c[x2 – (87.5)2]
= (x – 87.5) [b + c(x + 87.5)]
⇒ ![]()

To find b and c, we use the group average method.
Divide the given data into two groups of 3 values each.

![]()

![]()
∴ the equation in X and Y is ![]()
⇒ ![]()
⇒ ![]()
⇒ ![]()
= 0.00358(X−168.4)
= 0.00358X−0.6029
⇒ Y = 0.00358X+2.4197−0.6029
⇒ Y = 0.00358X+1.8168

Exercises 8.2
By the method of group averages fit the indicated curve.
(1) Fit y = ax + b to the data
|
x |
50 |
70 |
100 |
120 |
|
y |
12 |
15 |
21 |
25 |
(2) The following numbers relate to the flow of water over a triangular notch:
|
H |
1.2 |
1.4 |
1.6 |
1.8 |
2.0 |
2.4 |
|
Q |
4.2 |
6.1 |
8.5 |
11.5 |
14.9 |
23.5 |
H denotes the head of water (in feet), Q the quantity (in cubic feet) of water flowing per second. If the law is Q = CHn, find the best values of C and n.
[Hint: log10Q = log10C + nlog10H; put Y = log10Q, A = log10C, X = log10H
⇒ Y = A + nX]
(3) Fit a curve of the form y = kxn given:
|
x |
25.9 |
259 |
2590 |
25900 |
|
y |
0.308 |
0.209 |
0.148 |
0.098 |
(4) Fit a curve of the form y = a + bx + cx2 for the data:
|
x |
2 |
2.5 |
3 |
3.5 |
4 |
4.5 |
5 |
5.5 |
6 |
|
y |
18 |
17.8 |
17.5 |
17 |
15.8 |
14.8 |
13.3 |
11.7 |
9 |
Answers 8.2
(1) y = 0.19x + 2.1 (2) C = 2.6, n = 2.5
(3) y = 0.2673x−0.0118 (4) y = 15.8 + 2.1x − 0.5x2
8.3 METHOD OF THE SUM OF EXPONENTIALS
We shall now discuss another type of curve fitting known as exponential curve fitting.
Let ![]() be the observed data for the variables x and y.
be the observed data for the variables x and y.
Let
![]() (1)
(1)
be the curve fitted to the data, where ![]() are constants to be determined. We shall assume n is fixed and is known.
are constants to be determined. We shall assume n is fixed and is known.
We know that ![]() is the solution of the differential equation of the form
is the solution of the differential equation of the form
![]() (2)
(2)
where ![]() are unknown constants and
are unknown constants and ![]() are the roots of the auxiliary equation
are the roots of the auxiliary equation
![]() (3)
(3)
By Froberg’s method (1965), we can compute the derivatives numerically at the n points and substitute in (2) which will result in a system of n linear equations in the n unknowns ![]() which can be solved. Then
which can be solved. Then ![]() can be obtained and finally
can be obtained and finally ![]() can be obtained from (1) by the method of least squares or the method of averages.
can be obtained from (1) by the method of least squares or the method of averages.
Thus ![]() is fitted to the given data
is fitted to the given data
Note: The drawback of this method is the unreliability of the results, because of the accuracy of the derivatives decreases as the order n increases.
We shall now discuss a method given by Moore in 1974 which gives more reliable results. For simplicity, we shall consider the case when ![]() .
.
Let the curve to be fitted to the data be
![]() (4)
(4)
This function is the solution of the second order differential equation
![]() (5)
(5)
where ![]() are constants to be determined and
are constants to be determined and ![]() are the roots of the auxiliary equation
are the roots of the auxiliary equation
![]() .
.
Let ‘a’ be the initial value of x.
Integrating (5) w.r.to x, we get

where
![]()
Again integrating w.r.to x, we get
![]()
⇒ ![]()
We know the formula
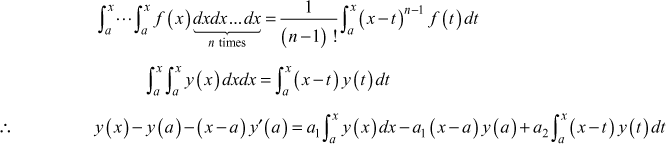 (6)
(6)
Let ![]() and
and ![]() be two data points such that
be two data points such that ![]() , then
, then
![]() (7)
(7)
and ![]() (8)
(8)

Taking two different ![]() and evaluating these integrals by numerical method, say Simpson’s
and evaluating these integrals by numerical method, say Simpson’s ![]() rule, we get two linear equations in
rule, we get two linear equations in ![]() and
and ![]() .
.
Solving these equations, we get ![]() and
and ![]() .
.
Solving ![]() , we get the values of
, we get the values of ![]() and
and ![]() .
.
Finally, we find the values of ![]() and
and ![]() by the method of least squares or averaging method.
by the method of least squares or averaging method.
Thus ![]() is fitted to the data.
is fitted to the data.
WORKED EXAMPLES
Example 1
Fit a function of the form ![]() to the following data.
to the following data.
|
x |
1 |
1.1 |
1.2 |
1.3 |
1.4 |
1.5 |
1.6 |
1.7 |
1.8 |
|
y |
1.175 |
1.336 |
1.510 |
1.698 |
1.904 |
2.129 |
2.376 |
2.646 |
2.942 |
Solution
The curve ![]() fitted to the given data is the solution of the differential equation
fitted to the given data is the solution of the differential equation
![]()
The auxiliary equation is
![]() (1)
(1)
Let ![]() be the roots of the auxiliary equation.
be the roots of the auxiliary equation.
The coefficients ![]() are given by
are given by
 (2)
(2)
where a is the initial value of x and x1 and x2 are two data points such that
![]()
To evaluate the integrals, we use Simpson’s ![]() rule.
rule.
So, we choose ![]() such that there are even number of intervals.
such that there are even number of intervals.
⇒ choose ![]()
⇒ ![]()
Substituting in (2), we get

The given table is
|
x |
1 |
1.1 |
1.2 |
1.3 |
1.4 |
1.5 |
1.6 |
1.7 |
1.8 |
|
y |
1.175 |
1.336 |
1.510 |
1.698 |
1.904 |
2.129 |
2.376 |
2.646 |
2.942 |

We shall evaluate these integrals by Simpson’s ![]() rule
rule

Now take ![]() and
and ![]() . We get
. We get ![]()

We shall evaluate these integrals by Simpson’s ![]() rule.
rule.


Substituting in (1), we get

We take ![]() and
and ![]()
∴ ![]()
To find ![]() and
and ![]() , we use the method of least squares
, we use the method of least squares
The sum of the squares of the residuals is
![]()
According to the method of least squares E is minimum if ![]() and
and ![]()

 (5)
(5)
 (6)
(6)
The equations (5) and (6) are called the normal equations.
Now we shall form the table for computation

Substituting in (5) and (6), we get
![]()
Dividing by 7.8267, we get
![]() (7)
(7)
and ![]()
Dividing by 0.4838, we get,
![]() (8)
(8)
![]()
Substituting in (7), we get

∴ ![]()
which is the equation of the curve fitted to the given data.
Example 2
Fit a curve of the form whose equation is ![]() , using the following data.
, using the following data.
|
x |
1 |
1.1 |
1.2 |
1.3 |
1.4 |
1.5 |
1.6 |
1.7 |
1.8 |
|
y |
1.54 |
1.67 |
1.81 |
1.97 |
2.15 |
2.35 |
2.58 |
2.83 |
3.11 |
Solution
The curve given by y = A1eλ1x + A2eλ2x fitted to the data is the solution of the differential equation
![]()
The auxiliary equation is
λ2 = a1λ + a2(1)
Let λ1, λ2 be the root of the auxiliary equation
The co-efficients a1, a2 are given by

Where a is the value of x and x1, x2 are two data points such that

To evaluate the integrals, we use Simpson’s ![]() rule.
rule.
So, we choose ![]() in such way that there are even number of intervals between
in such way that there are even number of intervals between ![]() and
and ![]() and the last value of x
and the last value of x
![]() choose
choose ![]() and
and ![]()
![]()
![]()
Substituting in (2), we get
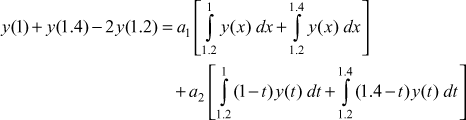
The given data is
|
x |
1 |
1.1 |
1.2 |
1.3 |
1.4 |
1.5 |
1.6 |
1.7 |
1.8 |
|
y |
1.54 |
1.67 |
1.81 |
1.97 |
2.15 |
2.35 |
2.58 |
2.83 |
3.11 |

We shall evaluate these integrals by Simpson’s ![]() rule.
rule.

∴ 
⇒ ![]()
Dividing by 0.0604, we get
![]()
Now take ![]() and
and ![]()
⇒ ![]()
Substituting in (2), we get

We shall evaluate these integrals by Simpson’s ![]() rule
rule


Dividing by 0.096, we get
![]() (4)
(4)

Substituting in (4), we get
⇒ ![]()
Substituting in (1), we get

We take ![]() and
and ![]()
⇒ ![]()
We shall now find ![]() ,
, ![]() by the method of least squares.
by the method of least squares.
The sum of the squares of the residuals is
![]()
According to the method of least squares E is minimum for the best fitted curve.
The normal equations are given by ![]() and
and ![]() .
.
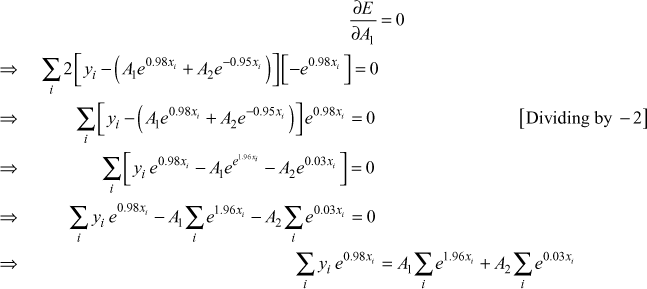 (5)
(5)
 (6)
(6)
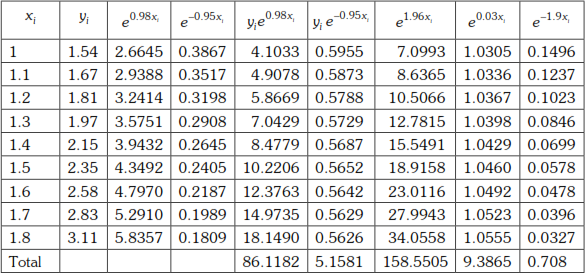
Substituting in the normal equations (5) and (6), we get
![]()
Dividing by 9.3685, we get
![]() (7)
(7)
and
![]()
Dividing by 0.708, we get
![]() (8)
(8)

Substituting in (8), we get
![]()
Take A1 = 0.52, and A2 = 0.39
∴ ![]()
Which is the equation of the curve fitted to the given data.
Exercise 8.3
(1) Fit a curve of the form ![]() for the following data
for the following data
|
x |
2 |
2.2 |
2.4 |
2.6 |
2.8 |
3.0 |
3.2 |
3.4 |
3.6 |
|
y |
3.63 |
4.46 |
5.47 |
6.70 |
8.19 |
10.02 |
12.25 |
14.97 |
18.29 |
Answer 8.3
(1) ![]()
8.4 METHOD OF MOMENTS
Let (x1, y1), (x2, y2), … (xn, yn) be a set of n observations of the related variables x and y.
Let the values of x be equally spaced with interval h = Δx, say
ie. xi− xi = Δx for all i = 1, 2, 3, ..., n − 1.
For such a set of points, we define
the first moment μ1 = Σy Δx = Δx Σy
the second moment μ2 = Σ xy Δx = Δx Σ xy
the third moment μ3 = Σ x2y Δx = Δx Σx2y and so on.
These moments are called the moments of the observed values of y.
Let y = f(x)be the curve to be fitted the data.
Then, the first moment g1 = ∫y dx = ∫f(x) dx
the second moment g2 = ∫xy dx = ∫xf(x) dx
and the third moment g3 = ∫x2y dx = ∫x2 f(x) dx and so on.
These moments are called the moments of the computed values of y or expected values of y.
The method of moments is based on the assumption that the moments of the observed values of y is equal to the moments of the expected values of y.
i.e. mI = ri ![]()
It can be proved that

These equations are known as observation equations.
If the form of f(x) is known, then using the observation equations the constants can be determined.
If f(x) is linear ie. f(x) = ax + b, then the equation of the curve fitted is y = ax + b
If 

Solving these two equations we find a and b and hence the equation y = ax+b
WORKED EXAMPLES
Example 1
By the method of moments, obtain a straight line to fit the data.
|
x |
1 |
2 |
3 |
4 |
|
y |
0.30 |
0.64 |
1.32 |
5.40 |
Solution
We fit a straight line to the given data by the method of moments.
Given values of x are equally spaced with Δx = 1.
Here x1 = 1, xn = 4
⇒ ![]()
Let the line fitted be y = ax+b (1)
Then, the observation equations are

Now ![]()
and ![]()
Substituting in (2) and (3) we get
![]()
![]() (4)
(4)
and
![]()
30.333a + 10b = 27.14
Dividing by 10, 3.0333a + b = 2.714(5)
(5) − (4) ⇒ ![]()
∴ b = 1.915 − 2.5(1.499) = −1.8325
∴ the equation of the straight line is y = 1.499x - 1.8325
Example 2
By method of moments fit a straight line to the data:
| x | 1 | 2 | 3 | 4 |
| y | 0.17 | 0.18 | 0.23 | 0.32 |
Solution
We fit a straight line to the given data by the method of moments.
Given values of x are equally spaced with ![]()
∴ ![]()
Let the line fitted be y = ![]() (1)
(1)
Then, the observation equations are
![]() (2)
(2)
![]() (3)
(3)
Now ![]()
Substituting in (2),
![]()
![]() (4)
(4)
Substituting in (3),
![]()
![]() (5)
(5)

Exercises 8.4
Fit a straight line by the method of moments to the following data:
|
x |
1 |
2 |
3 |
4 |
|
y |
16 |
19 |
23 |
26 |
Fit a straight line by the method of moments to the following data:
|
x |
1 |
3 |
5 |
7 |
9 |
|
y |
1.5 |
2.8 |
4.0 |
4.7 |
6.0 |
Fit a straight line by the method of moments to the following data:
| x |
1 |
2 |
3 |
4 |
| y |
1.7 |
1.8 |
2.3 |
3.2 |
Fit a straight line by the method of moments to the following data:
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 66.7 | 72.7 | 82.3 | 92.1 | 93 | 100 |
Answers 8.4
(1) y = 3.188x + 13.03 (2) y = 0.5231x + 1.1845
(3) y = 0.49x + 1.025 (4) y = 6.86x + 67.4
SHORT ANSWER QUESTIONS
1. What is meant by curve fitting?
2. State the principle of least square.
3. Define residual.
4. Write the normal equations to fit a straight line of the form ![]()
5. Write down the normal equations to fit a quadratic curve by the method of least squares.
6. Define the method of group averages.
7. Convert the equation ![]() into a linear form where a and b are constants.
into a linear form where a and b are constants.
8. Convert ![]()
9. Convert the equation ![]() into linear form.
into linear form.
10. Convert ![]() into linear form.
into linear form.
11. What is Gauss’s least square principal.
12. Convert ![]() into linear form.
into linear form.
13. Explain method of group Averages.
14. What is the defect of method of group averages?
15. How to avoid the defect of method of group averages?
16. ![]() is fitted by the method of moments.
is fitted by the method of moments.
17. Convert ![]() into linear form.
into linear form.
18. Convert ![]() into linear form.
into linear form.
19. Convert ![]() into linear form.
into linear form.
![]() to a linear form and write the corresponding normal equations to fit it.
to a linear form and write the corresponding normal equations to fit it.
