11.0 INTRODUCTION

Difference equations may be considered as the discrete analogue of differential equations. Discrete functions occur in many physical and engineering problems. So, difference equations are the natural choice for dealing with discrete situations.

Basic concepts of difference equations are similar to differential equations.

Definition 11.1: Difference equation

A difference equation is an equation involving an independent variable x, dependent variable y_x and the successive differences of yx or successive values yx, yx₊₁, yx₊₂ ...

1. Example (1)
2. 
3. are difference equations.

Since , every difference equation can be expressed in terms of the successive values

Definition 11.2: Order of the difference equation

The order of the difference equation is the difference between the highest and lowest suffixes of y_x involved in it.

1. Example (1) order of y_x+2 3^x is x 2.
2. order of Δ²y_x cos x is 2, since the highest difference is of order 2.
3. order of Δ²y_x x² is 2.

Definition 11.3: Degree of a difference equation

The degree of a difference equation expressed in terms of values is the highest power of the y’s.

The degree of the difference equations (1), (2), (3) in the example is 1.

But the degree of is 3.

Definition 11.4: Solution of a difference equation

The solution of a difference equation is a function which satisfies it.

Definition 11.5: General solution of a linear difference equation

The general solution of a linear difference equation of order n is a solution which contains n arbitrary constants.

Definition 11.6: Particular solution

A particular solution of a difference equation is a solution obtained from the general solution by giving particular values to the arbitrary constants.

For example: is the general solution of the difference equation.

Putting A = 1, B = –1, we get the particular solution y_x = 2^x − 3^x

11.1 LINEAR DIFFERENCE EQUATION

The general form of a linear difference equation of order r with constant coefficients is

(1)

where are constants.

The equation of the form

(2)

is called the corresponding homogenous linear difference equation of order r.

11.2 SOLUTION OF A DIFFERENCE EQUATION

As in the case of linear differential equations, we have the following results for linear difference equations.

1. If are r independent solutions of the linear difference equation (2), then their linear combination where are constants, is also a solution of (2).

This solution containing r arbitrary constants is called the general solution of (2).

The general solution of (2) is called the complementary function of (1).

If u_x is a particular solution of (1), then is the general solution of (1).

If the particular solution is denoted by P.I and the complementary function is denoted by C.F, then the solution is y_x = C.F + P.I.

Note: In the linear difference equation yx, yx₊₁,... occur in the first degree and there is no product of yx, yx₊₁,... occur in the equation. This is a characteristic of linear difference equation.

11.3 FORMATION OF A DIFFERENCE EQUATION

A difference equation is formed by eliminating the arbitrary constants in an ordinary relation between the variables.

WORKED EXAMPLES

Example 1

Form the difference equation corresponding to the family of curves y=ax + bx².

Solution

Given y = ax + bx²

Here y_x = y

∴ yx = ax + bx²

Since yx is a polynomial of degree 2, the second order differences are constants.

So, we consider 3 values and get three equations

(1)

(2)

(3)

From this system of linear equations in a and b, the eliminant of a and b is

Expanding this determinant by first column, we get

which is the required difference equation.

Example 2

Form the difference equation by eliminating a and b using

Solution

Given (1)

∴ (2)

and (3)

From this system of linear equations in a and b, the eliminant of a and b is

which is the required difference equation.

Example 3

Derive the difference equation, given

Solution

Given

(1)

∴ (2)

and

(3)

Treating these equations as linear equations in A and B, the eliminant of A and B is

which is the required difference equation.

Example 4

Find the difference equation generated by

Solution

Given

Denoting y by yx, we get

∴

and

Treating these equations as simultaneous linear equations in a and b, the eliminant of a and b is

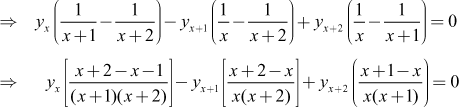
Multiplying by x(x + 1) (x + 2), we get

which is the required difference equation.

Example 5

Form the difference equation satisfied by the Fibonacci sequence 1, 1, 2, 3, 5, 8, …

Solution

Let yn denote the n^th term of the sequence 1, 1, 2, 3, 5, 8, 13, …

We observe that any term starting with the third term is the sum of the proceeding two numbers

and

This is the difference equation of the Fibonacci sequence.

Note: The general term of any sequence is usually denoted by any of these symbols y_n, y(n), y_k, y(k) y_x, y(x) etc.

Example 6

Find the difference equation with initial conditions to find the number of n – bit strings that do not have two consecutive zeros. Hence find the number of 5 bit strings.

Solution

Let yn denote the number of n − bit strings that do not contain two consecutive zeros.

Then the sequence {yn} gives all terms.

We have to find the difference equation satisfied by this sequence {yn},

If n = 1, the string is 1 − bit string, So, it is 0 or 1.

Hence it does not contain two zeros.

∴ y₁ = 2

If n = 2, the string is a 2 − bit string which may be 11,10,01,00

So, there are three 2-bit strings not containing two zeros.

∴ y₂ = 3

Now assume n ≥ 3

we shall consider an arbitrary n-bit string having no two consecutive zeros.

It may end with 0 or 1.

Case (i): Suppose the n-bit string ends with zero, then the (n − 1)^th bit must be 1 and there is no restriction on the (n − 2)^th bit.

∴ the number of n-bit strings ending with zero is yn − _2.

Case (ii): Suppose the n-bit string ends with 1, then the (n − 1)^th bit can be 1 or 0.

∴ the number of such strings is y_{n − 1}.

∴ the total number of n-bit strings with no two consecutive zeros is

yn = yn 3 with the conditions y₁ = 2, y₂ = 3

So, the number of 5-bit strings is y₅ = y₄ + y₃

But y₄ = y₃ + y₂

y₃ = y₂ + y₁ = 3 = 5

∴ y₄ = 5 + 3 = 8

and y₅ = 8 + 5 = 13

Exercises 11.1

Find the difference equation satisfied by

1. 
2. 
3. 
4. 

Answers 11.1

1. 
2. 
3. 
4. 

11.4 LINEAR HOMOGENEOUS DIFFERENCE EQUATION WITH CONSTANT COEFFICIENTS

The general form of a linear homogeneous difference equation with constant coefficients is

(1)

Let be a trial solution of (1)

Substituting in (1), we get

(2)

The equation (2) of degree k in m is called the auxiliary equation or the characteristic equation of (1).

Let m₁, m₂, m₃, … , m_k be the roots of (2).

Depending on the nature of roots we have the solution of (1)

Case (1): The roots are all real and different

If the roots m₁, m₂, m₃, … , m_k are real and different, then

is

the general solution of (1), where c₁,c₂, …,c_k are arbitrary constants

Case (2): Some roots are real and repeated

If m₁ = m₂ = m and m₃,m₄, …, mk are different, then

is the general solution of (1), where c₁, c₂, c₃..,c_k are arbitrary constants.

Suppose m₁ = m₂ = m₃ = m₄ = m and m₅, m₆, .., m_k are different, then the general solution is

Case (3): Non-repeated complex roots

Let be the complex roots and m₃, m₄,…, m_k are real and different.

Then the general solution is

.

where and

Let be repeated complex roots and m₅, m₆,…, m_k are real and different roots.

Then the general solution is

where , and c₁, c₂, c_3,…, c_k are arbitrary constants.

11.4.1 Working Rule

(1) The equation (1) can be written as

(2) Replacing E by m, we get the auxiliary equation

(3) If m₁, m₂, m₃,…,m_k are the roots, then we can write the general solution as discussed in case (1), (2) and (3)

11.5 SOME BASIC RESULTS OF DIFFERENCE OPERATOR TO SOLVE DIFFERENCE EQUATIONS

Let us take be the first difference of the function F(x), then

Now

= F(n + 1) − F(1)

, in symbols.

Note:

1. Thus Δ−¹ is an operator, when operated on a function f(x) yields F(x) whose first difference is f(x). So we find Σ behaves like Δ−¹
2. The above finite difference summation is sometimes referred to as finite integration, Since it employs the operator Δ−¹, similar to D−¹ in integral calculus.
3. Since

We have the following table of finite integrals

1. 
2. 
3. 
4. 
5. 
6. 

This is called the rule for finite integral by parts.

Note:

WORKED EXAMPLES

Example 1

Obtain the solution of the difference equation

Solution

The given equation is

Auxiliary equation is m − 5 = 0, ∴ m = 5.

The root is real

the general solution is

Example 2

Obtain the solution of the difference equation

Solution

The given equation is

Auxiliary equation is 3m + 2 = 0

The root is real.

the general solution is

Example 3

Solve the difference equation

Solution

The given equation is

auxiliary equation is

∴ (m – 4) (m – 2) = 0 ∴ m = 2, 4

The roots are real and different

∴ the general solution is

Example 4

Solve

Solution

The given equation is

Auxiliary equation is

The roots are real and equal.

∴ the general solution is

Example 5

Solve

Solution

The given equation is

∴

∴

Auxiliary equation is

∴

The roots are complex with and

and

the general solution is

Example 6

Solve with the condition

Solution

The given equation is

∴

∴

The roots are real and distinct.

the general solution is (1)

Given and

Putting n = 0 and 1 in (1), we get

∴ (2)

and

∴

∴

∴

∴ particular solution is

Example 7

Solve the difference equation given

Solution

The given equation is

Auxiliary equation is

Since the sum of the coefficients is zero, m = 1 is a root.

The other roots are given by

∴

∴

the roots are m = 1, 1, –2 with two equal roots

the general solution is

∴ (1)

Given

putting n = 1, 2, 3 in (1), we get

∴

∴ (2)

∴

∴ (3)

and

∴

∴ (4)

Adding (5)

Adding (6)

Substituting in (5), ∴

Substituting in (2), ∴

the particular solution is

Example 8

If satisfies the difference equation

and the conditions then show that is a solution if sin α ≠ 0, where α a is constant.

Solution

The given equation is

Rewrite the equation replacing k by k + 1

Auxiliary equation is

∴

The roots are complex with ‘a’ = cos a, ‘b’= sin a

and

the general solution is

∴ (1)

Given

Putting k = 0 and 1 in (1), we get

∴

and

∴

Particular solution is

∴

Exercises 11.2

Solve the following linear homogenous difference equation.

(1) (2)

(3) (4)

(5) (6)

(7) (8)

(9) (10)

(12)

Answers 11.2

(1) (2)

(3) (4)

(5) (6)

(7) (8)

(9) ,

(11)

11.6 NON-HOMOGENEOUS LINEAR DIFFERENCE EQUATIONS WITH CONSTANT COEFFICIENTS

The general form of non-homogeneous linear difference equation with constant coefficients is

(1)

where are constants.

The equation (1) can be written as

∴ (2)

To fi nd the complementary function, solve

(3)

The general solution of (3) is called the complementary function of (1).

To find the complementary function

Refer 11.4, page

The particular solution is usually called particular integral and denoted as P.I.

The general solution of (1) is

11.6.1 Evaluation of Particular Integrals

1. Particular Integral – Type I:

If then

If then is a factor of

where

[Refer 11.5 page,…]

WORKED EXAMPLES

Example 1

Solve

Solution

The given equation is

∴

∴

To find the complementary function, solve

Auxiliary equation is m − 5 = 0 ∴ m = 5

P.I =

∴ the general solution is

∴

Example 2

Solve the difference equation

Solution

The given equation is

∴

∴

To find the complimentary function solve

Auxiliary equation is m − 4 = 0 ∴ m = 4

∴

∴ the general equation is

∴

Example 3

Solve the difference equation where a and b are constants.

Solution

The given equation is

∴

∴

To find the complementary function, solve

Auxiliary equation is m + a = 0 ∴ m = − a

∴

∴ the general equation is

∴

Example 4

Solve where y₀ = 2, y₁ = 1.

Solution

The given equation is

∴

∴

To find the complementary function, solve

Auxiliary equation is

⇒ The roots are real and equal.

∴

P.I =

∴ the general solution is

∴ (1)

Given y₀ = 2, y₁ = 1

Putting x = 0 and 1 in (1), we get

∴

and

∴ ∴

∴ the solution is

Example 5

Solve the difference equation where y₀ = 0, y₁ = 1.

Solution

The given equation is

∴

∴

To find the complementary function, solve

Auxiliary equation is

∴

∴

P.I =

∴ the general solution is

∴ (1)

Given y₀ = 0, y₁ = 1

Putting x = 0 and 1 in (1), we get

∴ (2)

and

∴

∴ (3)

(3)− (2) ∴ C₂ = 0

∴

∴ the solution is

Example 6

Solve the difference equation

Solution

the given equation is

∴

∴

∴

To find the complementary function, solve

Auxiliary equation is ∴

The roots are real and equal.

∴

∴ the general solution is y_x = C.F + P.I

∴

∴

∴

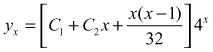
Example 7

Solve the difference equation

Solution

the given equation is

∴

∴

∴

To find the complementary function, solve

Auxiliary equation is (m − 1)² = 0 ∴ m = 1, 1

The roots are real and equal

∴

∴ the general solution is

∴

Example 8

Solve the equation

Solution

The given equation

∴

∴

To find the complementary function, solve

Auxiliary equation is

Since sum of the coefficients is zero, m = 1 is a root.

The other roots are given by

∴

∴ the roots are m₁ = 1, m₂ = 2, m₃ = 2 with two equal roots.

∴

∴ the general solution is

∴

If where r is a non – negative integer, then

Expanding as a polynomial in Δ,

WORKED EXAMPLES

Example 9

Solve the difference equation

Solution

The given equation is

∴

∴

To find the complementary function, solve

Auxiliary equation is ∴

∴

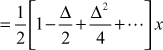
∴ the general solution is

∴

Example 10

Solve the equation

Solution

The given equation is

∴

∴

To find the complementary function, solve

Auxiliary equation is

∴

Now

and

∴

∴ the general solution is

∴

Example 11

Solve the difference equation

Solution

The given equation is

∴

∴

To find the complementary function, solve

Auxiliary equation is

∴

Now

and

∴

∴ the general solution is

∴

Example 12

Solve the equation

Solution

The given equation is

∴

∴

To find the complementary function solve

Auxiliary equation is

∴

∴

Now

 

and

∴

We shall express in factorial polynomial form.

We know that

∴

and

∴

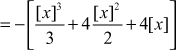
∴ the general solution is

∴

Example 13

Solution

The given equation is

∴

∴

To find the complimentary function, solve

Auxiliary equation is

∴

The roots are complex with

∴

and

∴

∴ the general solution is

∴

If , where g(x) is a polynomial in x, then

WORKED EXAMPLES

Example 14

Solve the difference equation .

Solution

The given equation is

∴

∴

To find the complementary function, solve

Auxiliary equation is

∴

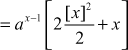
∴ the general solution is

Example 15

Solve the difference equation

Solution

The given equation is

∴

∴

To find the complementary function, solve

Auxiliary equation is m − 2 = 0 ∴ m = 2

∴

Now

and

∴

∴ the general solution is

∴

Example 16

Solve the difference equation .

Solution

The given equation is

∴

∴

To find the complementary function, solve

Auxiliary equation is

∴

∴

Now

and

∴

∴the general solution is

∴

Example 17

Solve the equation

Solution

The given equation is

∴

∴

To find the complementary function, solve

Auxiliary equation is

∴

∴

Now

and

∴

∴the general solution is

∴

Example 18

Solve the difference equation

Solution

The given equation is

∴

∴

To find the complementary function, solve

Auxiliary equation is

∴

∴

Now

and

∴

∴ the general solution is

∴

If

then

(i) If , then

, where ,

which can be obtained by type 1.

If , then

, where ,

which can be obtained by type 1.

WORKED EXAMPLES

Example 19

Solve the equation

Solution

The given equation is

∴

∴

To find the complementary function, solve

Auxiliary equation is

∴

[Refer 11.5, page,...]

∴ the general solution is

∴

Example 20

Solve

Solution

The given equation is

∴

∴

∴

∴

∴

To find the complementary function, solve

Auxiliary equation is ∴

∴

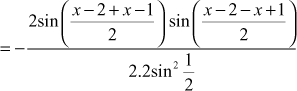
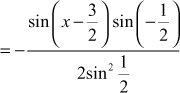
∴ the general solution is

∴

Example 21

Solve the difference equation

Solution

The given equation is

∴

∴

To find the complementary function, solve

Auxiliary equation is

∴

, where

∴

∴ the general solution is

∴

Example 22

Solve the equation

Solution

The given equation is

∴

∴

To find the complementary function, solve

Auxiliary equation is

∴

∴

∴

The roots are

Here

∴

and

∴

∴

, where

∴

∴ the general solution is

∴

If

where

and

then

∴ the general solution is

WORKED EXAMPLES

Example 23

Solve

Solution

The given equation is

∴

∴

To find the complementary function, solve

Auxiliary equation is m + 3 = 0 ∴m = − 3

∴

where

and

∴ the general solution is

Example 24

Solve the difference equation

Solution

The given equations is

∴

∴

To find the complementary function, solve

Auxiliary equation is m − 2 = 0 ∴ m = 2

∴

where

and

∴ the general solution is

∴

∴

Example 25

Solve the difference equation

Solution

The given equation is

∴

∴

To find the complementary function, solve

Auxiliary equation is

∴

∴

where

and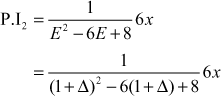

∴ the general solution is

∴

Example 26

Solve the difference equation

Solution

The given equation is

Replacing x by x + 2, we get

∴

∴

To find the complementary function, solve

Auxiliary equation is

∴

∴

where

and

∴ the general solution is

Exercises 11.3

Solve the following non-homogeneous differential equations.

1. 
2. 
3. 
4. 
5. 
6. 
7. given
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 

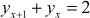
Answers 11.3

1. 
2. 
3. 
4. 
5. 
6. sin
7. 
8. 
9. 
10. 
11. 
12. 
13. (14) (15)

11.7 FIRST ORDER LINEAR DIFFERENCE EQUATION WITH VARIABLE COEFFICIENTS

11.7.1 First Order Linear Homogeneous Difference Equation with Variable Coefficients

Consider the homogeneous linear equation

∴

Putting x = 0, 1, 2,.., x – 1, we get where

If a constant, then is the solution of the given equation

If then we give the values of x from 1 to x – 1.

∴ we get

where is a constant, which is the solution of the given equation

WORKED EXAMPLES

Example 1

Solve

Solution

The given equation is

∴

Put x = 1, 2, 3,…, x – 1, then

If is a constant, then the solution is

∴

Example 2

Solve if

Solution

The given equation is

∴

Put x = 2, 3, 4 ,…, x – 1, then we get

is the solution of the given equation.

Example 3

Solve

Solution

The given equation is

∴

Put x = 1, 2, 3,…, x − 1, then we get

If a constant, then

∴

∴ is the solution of the given equation.

11.7. 2 First Order Linear Non-homogeneous Difference Equation with Variable Coefficients

Consider the equation

(1)

∴ the homogeneous equation is (2)

We can find the solution of (2) by 17.7.1, page…

Let be the solution of (2)

∴ (3)

Let be the solution of (1)

Then

Substituting in (1), we get

∴ [using (3)]

∴

∴

∴

∴

∴

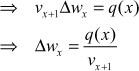
which is the solution of (1).

WORKED EXAMPLES

Example 4

Solve the difference equation

Solution

The given equation is (1)

Here

Consider (2)

∴

Put x = 0, 1, 2, 3, …, (x – 1), then we get

= k x!, where y₀ = k

Let be the solution of (2)

Let be the solution of (1)

∴ ∴

Example 5

Solve the difference equation

Solution

The given equation is (1)

Here

Consider (2)

∴

Putting x = 1, 2, 3,…, (x – 1), we get

∴

[ sum of first n odd numbers is n². Here n =x – 1].

Take

∴

∴ the general solution of (1) is

∴ , where

Exercises 11.4

(2) Solve

(4) Solve

Answers 11.4

(2) (3)

(5)

Short Answer Questions

1. Define a difference equation.
2. What is the solution of the difference equation?
3. Define the general solution of difference equation.
4. Define the particular solution of a difference equation.
5. What is the order of the difference equation?
6. What is the degree of the difference equation?
7. Is Δ²y_x + 2Δy_x + y_x =x² a difference equation?
8. Form the difference equation by eliminating a and b from the relation y_x = a.2^x + b.3^x.
9. Form the difference equation by eliminating A and B from y_x = A.2^x + B.5^x.
10. Form the difference equation by eliminating a and b from the relation y_x = a.2^x −2)^x.
11. Solve
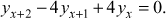
12. Solve the difference equation
13. Show that is a solution of the difference equation.
14. Find the solution of
15. Find the solution of
16. Find the solution of
17. Solve
18. Solve
19. Solve
20. Find the solution of the difference equation
21. Find the P.I of
22. Find the particular Integral of
23. Find the particular integral of
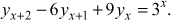
24. Find the particular integral of