7
Numerical Integration
7.0 INTRODUCTION
We know that  can be evaluated if there exists a differentiable function F such that
can be evaluated if there exists a differentiable function F such that ![]() in
in ![]() However, in applications we come across integrals of the form
However, in applications we come across integrals of the form  which cannot be evaluated in closed form or analytical form. Sometimes
which cannot be evaluated in closed form or analytical form. Sometimes ![]() is given by a set of recorded values
is given by a set of recorded values
![]()
In such cases we use the method of numerical integration.
Numerical Integration is the process of evaluating a definite integral  from a set of tabulated values of the integrand
from a set of tabulated values of the integrand ![]() , which is not known or complicated. This process is known as mechanical quadrature.
, which is not known or complicated. This process is known as mechanical quadrature.
Geometrically,  represents the area bounded by the curve
represents the area bounded by the curve ![]() and the x-axis between
and the x-axis between ![]() and
and ![]()
The process of Numerical integration is carried out by first approximating the integrand ![]() by an interpolating polynomial
by an interpolating polynomial ![]() and then integrating between the given limits. Thus
and then integrating between the given limits. Thus  is approximately equal to
is approximately equal to 
We shall now derive a general quadrature formula for equidistant ordinates based on Newton’s forward difference formula.
7.1 A GENERAL QUADRATURE FORMULA OR NEWTON-COTES QUADRATURE FORMULA
Let  be the integral to be evaluated.
be the integral to be evaluated.
Divide ![]() into n subintervals each of equal length
into n subintervals each of equal length ![]()
Let ![]() be the points of division of
be the points of division of ![]() so that
so that
![]()
![]()
Let ![]() be the values of the function
be the values of the function ![]() at the points
at the points ![]() respectively.
respectively.
Newton’s forward difference formula for this data ![]() is
is
![]()
where
![]()
![]()
When
![]()
![]()
∴ 
 (1)
(1)
From this general formula we deduce some important quadrature formulae by putting ![]()
7.2 TRAPEZOIDAL RULE
The trapezoidal rule is

Newton-Cotes formula is
 (1)
(1)
Put n = 1 in (1), then we get

Because in this case, we have only two points ![]() and
and ![]() of x and the values y0 and y1 of y, the second and higher differences are zero
of x and the values y0 and y1 of y, the second and higher differences are zero

![]()


This is known as trapezoidal rule. This is also known as general form of Trapezoidal rule or composite trapezoidal rule.
7.2.1 Geometrical meaning
The integral  represents the area bounded by the curve
represents the area bounded by the curve ![]() the x-axis and the ordinates
the x-axis and the ordinates ![]() and
and ![]()
In trapezoidal rule the curve ![]() is replaced by n straight line segments joining the points
is replaced by n straight line segments joining the points ![]() and
and ![]() and
and ![]() and
and ![]()
The sum of the areas of these trapeziums is taken as the area under the curve.
Hence the name Trapezoidal rule.
WORKED EXAMPLES
Example 1
Dividing the range into 10 equal parts, find the approximate value of  by Trapezoidal rule.
by Trapezoidal rule.
Solution
Given  .
.
Here ![]() The interval is
The interval is ![]()
The interval ![]() is divided into 10 equal parts.
is divided into 10 equal parts.
∴ ![]()
The values of x are ![]() .
.
We shall find the values of ![]() at these points
at these points ![]()

By Trapezoidal rule,

Example 2
Evaluate ![]() using trapezoidal rule taking h = 0.25.
using trapezoidal rule taking h = 0.25.
Solution
Given
![]()
Here
![]()
∴ the ponits are x0 = 0, x1 = 0.25, x2 = 0.5, x3 = 0.75,
x4 = 1, x5 = 1.25, x6 = 1.5, x7 = 1.75, x8 = 2,
We shall find the values of y and they are given by the table below.

By Trapezoidal rule,

Example 3
A rocket is launched from the ground. Its acceleration is registered during the first 80 seconds and it is in the table below. Using trapezoidal rule find the velocity of the rocket at t = 80 secs.
| t secs | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| f : cm/sec2 | 30 | 31.63 | 33.34 | 35.47 | 37.75 | 40.33 | 43.25 | 46.69 | 40.67 |
Solution
Let v and a be the velocity and acceleration at time t
Given a = f(t) cm/sec2
∴ ![]()
We use trapezoidal rule to find the velocity v, when t = 80 secs
∴ 
They given table is

Here n = 8, and h = 10
By Trapezoidal rule,

∴ when t = 80 secs, the velocity is v = 3037.95 cm/sec
Example 4
Evaluate ![]() using the following table by trapezoidal rule.
using the following table by trapezoidal rule.
| x | 4 | 4.2 | 4.4 | 4.6 | 4.8 | 5 | 5.2 |
| 1.3863 | 1.4351 | 1.4816 | 1.5261 | 1.5686 | 1.6094 | 1.6487 |
Solution
The given table is

Here ![]()
By Trapezoidal rule,

Example 5
Evaluate ![]() dividing the range into 4 equal parts by Trapezoidal rule.
dividing the range into 4 equal parts by Trapezoidal rule.
Solution
Given ![]()
Here ![]() . Interval is
. Interval is ![]()
The interval ![]() is divided into 4 equal parts.
is divided into 4 equal parts.
∴ ![]()
∴ the points are ![]()
We find the values of ![]() at these points and they are given by the table below.
at these points and they are given by the table below.

By Trapezoidal rule,

7.3 SIMPSON’S RULE OR SIMPSON’S  RULE
RULE
Simpson’s rule is 
Proof: In the general quadrature formula put ![]() .
.
Then the interval is ![]() to
to ![]() . So, the points are
. So, the points are ![]() ,
, ![]() ,
, ![]() and the values of y are
and the values of y are ![]() respectively.
respectively.
Since three values are given, third and higher differences are zero

⇒ 
Similarly,

Adding, we get

where n is a multiple of 2.
That is the number of sub-intervals should be 2, 4, 6, 8, . . .
This formula is called Simpson’s rule or Simpson’s ![]() rule.
rule.
It is also known as composite Simpson’s ![]() rule.
rule.
7.3.1 Geometrical meaning
In Simpson’s method in each interval ![]()
![]() where n is even, the curve
where n is even, the curve ![]() is replaced by a second degree polynomial or parabola.
is replaced by a second degree polynomial or parabola.
That is the curve ![]() is replaced by
is replaced by ![]() arcs of parabola. So, the area under the curve
arcs of parabola. So, the area under the curve ![]() is taken as sum of the areas under the
is taken as sum of the areas under the ![]() parabolic arcs.
parabolic arcs.
The dotted line is the graph of ![]() and the thick lines are various parabolae.
and the thick lines are various parabolae.

WORKED EXAMPLES
Example 1
Evaluate ![]() by dividing the interval into eight equal parts and hence find the approximate value of
by dividing the interval into eight equal parts and hence find the approximate value of ![]()
Solution
Given 
Here ![]()
The interval is [2, 10].
We divide the interval into eight equal parts ∴ ![]()
So, we use Simpson’s ![]() rule to find
rule to find 
The points are ![]()
The values of y at these pernts are given by the table below.

By Simpson’s formula,

By direct integration,
∴ 
Note: But the value of ![]() correct upto 5 places.
correct upto 5 places.
So, we find Simpson’s formula gives the value correctly to 3 decimal places.
Example 2
A rocket is launched from the ground. Its acceleration is registered during the first 80 seconds and it is in the table below. Using Simpson’s ![]() rule, find the velocity of the rocket at t = 80 secs.
rule, find the velocity of the rocket at t = 80 secs.
| t secs | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| f : cm/sec2 | 30 | 31.63 | 33.34 | 35.47 | 37.75 | 40.33 | 43.25 | 46.69 | 40.67 |
Solution
Let v be the velocity of the rocket at t secs,
∴ 
When 
Given table is

Here n = 8, h = 10
By Simpson’s ![]() rule,
rule,

∴ when t = 80 secs, the velocity is v = 3052.77 cm/sec
Example 3
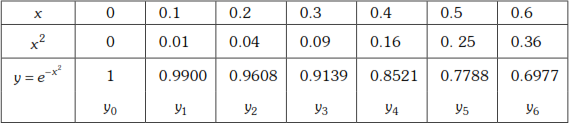
Use Simpson’s ![]() rule to find
rule to find ![]() by taking seven ordinates.
by taking seven ordinates.
Solution
Given 
Here ![]()
The interval is [0, 0.6] and divide the interval into six equal parts and so there will be seven ordinates.
![]()
The points are ![]()
Now we shall find the values of ![]() at these points are given by the table below.
at these points are given by the table below.
By Simpson’s ![]() rule,
rule,

![]()
Example 4
The following table gives the velocity u of a particle at time t:
| t (secs) | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| v (m/sec) | 4 | 6 | 16 | 34 | 60 | 94 | 136 |
Find the distance moved by the particle in 12 secs and also the acceleration at t = 2 secs.
Solution
Let s be the distance moved at time t
Let v and a be the velocity and acceleration at time t.
We know that velocity ![]() and acceleration
and acceleration![]()
∴ 
When t = 12 secs, the distance travelled  , where y = v
, where y = v
The values of y are given by the table.

By Simpson’s ![]() rule,
rule,

∴ when t = 12, distance moved is s = 552 meters
We want acceleration when t = 2 sec.
⇒ ![]()
ie. we want to find the derivative of v.
So, we form the difference table.

Newton’s forward formula is
![]()
where ![]()
When ![]()

∴ when t = 3 secs, the acceleration is a = 3 m/sec2
Example 5
Evaluate ![]() using Simpson’s
using Simpson’s ![]() rule, given that
rule, given that
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 0 | 1 | 4 | 9 | 16 | 25 |
Solution
Let 
Here ![]()
The number of intervals is 6 and h = 1 ∴ n = 6, a multiple of y2.
So, we can use Simpson’s ![]() rule
rule
The points are ![]()
The values of y are given by the table below.

By Simpson’s rule,

Example 6
A solid of revolution is formed by rotating about the x-axis, the area between the x-axis and the lines x = 0, x = 1 and a curve through the points with the following coordinates.
| x | 0.0 | 0.25 | 0.50 | 0.75 | 1 |
| y | 1 | 0.9896 | 0.9589 | 0.9089 | 0.8415 |
Estimate the volume of the solid formed using Simpson’s rule.
Solution
The volume v of solid of revolution about the x-axis, the area between the curve ![]() the x-axis and the lines x = 0 and x = 1 is
the x-axis and the lines x = 0 and x = 1 is 
The interval [0, 1] is divided into four equal parts with h = 0.25
∴ n = 4, a multiple of 2.
So, we can use Simpson’s ![]() rule to find the required volume
rule to find the required volume 
The points are ![]()
The values of ![]() are given by the table below.
are given by the table below.

By Simpson’s rule,

∴ volume v = 2.8193 cubic units
7.4 Simpson’s  rule
rule
Simpson’s ![]() rule is
rule is

Proof: We derive the formula using the general quadrative formula.
In the general quadrature formula, put n = 3
Then the interval is ![]() and the four values of y are
and the four values of y are ![]()
So, the fourth and higher differences are zero

Now ![]()


∴ 
Similarly,

Adding we get

where n is a multiple of 3.
This formula is called Simpson’s ![]() rule.
rule.
This formula is also known as Composite Simpson’s ![]() rule.
rule.
Note: For applying Simpson’s ![]() rule, the number of sub-intervals of
rule, the number of sub-intervals of ![]() should be a multiple of 3. Usually we divide into 6 or 9 sub-intervals.
should be a multiple of 3. Usually we divide into 6 or 9 sub-intervals.
7.4.1 Geometrical Meaning
In Simpson’s ![]() rule, in each interval,
rule, in each interval,
![]()
![]()
Where n is a multiple of 3, the curve ![]() is replaced by
is replaced by ![]() are of a cubic polynomials.
are of a cubic polynomials.
So, the area under the curve ![]() is taken as the sum of the areas under the
is taken as the sum of the areas under the ![]() arcs of the cubic polynomial.
arcs of the cubic polynomial.
The dotted line is the curve ![]() and the thick lines are various arcs of the cubic polynomials.
and the thick lines are various arcs of the cubic polynomials.

WORKED EXAMPLES
Example 1
Evaluate ![]() taking 7 ordinates by applying Simpson’s
taking 7 ordinates by applying Simpson’s ![]() rule. Deduce the value of loge2.
rule. Deduce the value of loge2.
Solution
Let 
Here ![]()
Since the number of ordinates is 7, the number of subintervals is 6.
![]()
∴ the points are ![]()
The values of y are y0, y1, y2, y3, y4, y5, y6 and they are given by the table below.

By Simpson’s ![]() rule,
rule,

![]()
But

Example 2
A curve is drawn to pass through the points given by the following table.
| x | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| y | 2 | 2.4 | 2.7 | 2.8 | 3 | 2.6 | 2.1 |
Using Simpson’s ![]() rule, estimate the area bounded the curve,
rule, estimate the area bounded the curve, ![]() the x-axis and the lines x = 1, x = 4.
the x-axis and the lines x = 1, x = 4.
Solution
Required area is A = ![]()
The given table is

Number of intervals is 6 and h = 0.5
∴ n = 6, a multiple of 3.
So, we can use Simpson’s ![]() rule to find the required area bounded by
rule to find the required area bounded by ![]() the x-axis and the lines x = 1, x = 4,
the x-axis and the lines x = 1, x = 4,
By Simpson’s ![]() rule,
rule,
A =
∴ area is ![]()
Example 3
A river is 60 ft wide. The depth y feet at a distance x ft from one bank is given by the following table.
| x | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| y | 0 | 4 | 7 | 9 | 12 | 15 | 14 |
Find approximately the area of cross-section.
Solution
The area of the cross-section is 
The given table is

Number of intervals is 6 and h = 10
∴ n = 6, a multiple of 3.
So, we use Simpson’s ![]() rule to find the area of the cross-section.
rule to find the area of the cross-section.
By Simpson’s ![]() rule,
rule,

∴ area of the cross-section is A = 547.5 sq.ft
Example 4
The velocity v of a particle at a distance s from a point on its path is given by the table
| s.ft | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| v ft/sec | 47 | 58 | 64 | 65 | 61 | 52 | 38 |
Estimate the time taken to travel 60 ft by using Simpson’s ![]() rule. Compare the result with Simpson’s
rule. Compare the result with Simpson’s ![]() rule.
rule.
Solution
Let s be the distance travelled and v be the velocity at time t secs.
∴ We know that velocity 
∴ 
∴ the time taken to travel s = 60 ft is ![]() . Let
. Let 
We shall form the table of values of y.

Here h = 10 and n = 6, even
By Simpson’s ![]() rule,
rule,
![]()
Here h = 10,
∴ 
By Simpson’s ![]() rule,
rule,

∴ the time taken by the particle to travel 60 ft by the two methods are equal, correct to 2 places of decimals.
Example 5
Evaluate  by using (i) direct integration (ii) Trapezoidal rule (iii) Simpson’s
by using (i) direct integration (ii) Trapezoidal rule (iii) Simpson’s ![]() rule (iv) Simpson’s
rule (iv) Simpson’s ![]() rule.
rule.
Solution
Let 
Here ![]()
Let ![]()
![]()
The parts are ![]()

(ii) Trapezoidal rule
By Trapezoidal rule,

(iii) Simpson’s ![]() rule
rule
By Simpson’s ![]() rule,
rule,

(iv) Simpson’s ![]() rule
rule
By Simpson’s ![]() rule,
rule,
![]()

(i) By direct integration

7.5 BOOLE’S RULE
Boole’s rule is

Proof: We derive the formula using the general quadrature formula
In the general quadrature formula, put ![]() then the interval is
then the interval is ![]() and the five values of y are
and the five values of y are ![]()
So, the fifth and higher differences are zero.

Now


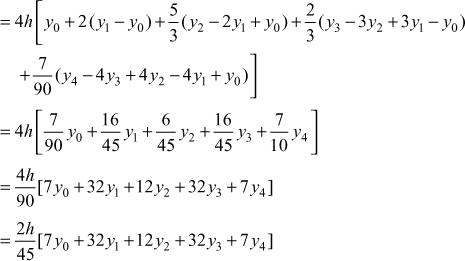
Similarly,

Adding all these integrals, we get

where n is a multiple of 4
ie the number of sub-intervals should be 4, 8, 12, ...
This formula is called Boole’s formula.
This formula is also known as composite Boole’s formula.
WORKED EXAMPLES
Example 1
Evaluate ![]() using Boole’s rule with
using Boole’s rule with ![]()
Solution
Let ![]()
Here ![]()
∴ number of sub-intervals is 4,
So, we can use Boole’s rule.
The points are ![]()
The values of y are y0, y1, y2, y3, y4 and they are given by the table below
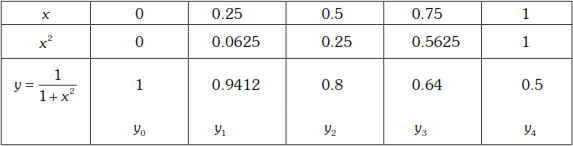
By Boole’s rule,

Example 2
Use Boole’s rule to estimate approximately the area of the cross-section if the river is 80 ft wide, the depth d ft at a distance x from one bank being given by the following table.
|
x |
0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| d | 0 | 4 | 7 | 9 | 12 | 15 | 14 | 8 | 3 |
Solution
Required area is ![]() where
where ![]()
Given table is

Number of interval is 8
∴ n = 8, a multiple of 4 and h = 10
So, we can use Boole’s rule to find the required area.
By Boole’s rule,

∴ the area of the cross–section is 708 sq.ft
Example 3
The velocity v of a particle at distance x from a point on its path is given below
| 0 | 10 | 20 | 30 | 40 | |
| 45 | 60 | 65 | 64 | 42 |
Find the time taken to cover the distance of 40 meters.
Solution
Let v be the velocity at time t.
Since x is given as the distance covered by a particle at time t, we know the velocity is

∴ the time taken to travel x = 40 is ![]()
The values of y are given by the table below

The number of value is 4 and h = 10 ∴ ![]()
So, we can use Boole’s rule to find ![]()
By Boole’s rule,

∴ the time taken to travel the distance 40 metres 0.6846 minutes
= 0.6648 × 60 secs = 41.076 secs
7.6 WEDDLE’S RULE
Weddle’s rule is

Proof: = 6, then the interval is ![]() is and the seven values
is and the seven values ![]() of y are involved.
of y are involved.
So, the seventh difference and higher difference are zero.

To rewrite the formula conveniently, replace ![]() by
by ![]() , as the error involved is negligible for small values of h.
, as the error involved is negligible for small values of h.

⇒ 
Similarly,

Adding all these integrals, we get

where n is the number of intervals and it is a multiple of 6.
That is the number of sub-intervals should be 6, 12, 18, …
This is known as Weddle’s rule.
WORKED EXAMPLES
Example 1
Evaluate ![]() by using Weddle’s rule.
by using Weddle’s rule.
Solution
Let ![]() (1)
(1)
Here ![]()
Divide the interval [0, 6] into 6 equal intervals.
∴ the number of sub-intervals is 6, a multiple of 6.
∴ ![]() and
and ![]()
So, we can use Weddle’s rule to find (1)
The points are ![]()
The values of y are y0, y1, y2, y3, y4, y5, y6 and they are given by the table below

By Weddle’s rule,

Example 2
A curve is drawn to pass through the points given by the following table.
| x | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| y | 2 | 2.4 | 2.7 | 2.8 | 3 | 2.6 | 2.1 |
Using Weddle’s rule, estimate the area bounded by the curve, the x-axis and the lines x = 1, x = 4.
Solution
The area bounded by the curve ![]() the x-axis and the lines
the x-axis and the lines ![]() is
is ![]()
The interval [1, 4] is divided into 6 equal parts with ![]()
∴ n = 6, a multiple of 6
So, we can use Weddle’s rule to find ![]()
The points are ![]()
The values of y are y0, y1, y2, y3, y4, y5, y6 and they are given by the table below.

By Weddle’s rule,

∴ the area is 7.74 sq. units
Example 3
Use Weddle’s rule to evaluate the approximate value of ![]() given that
given that
| x | 4.0 | 4.2 | 4.4 | 4.6 | 4.8 | 5 | 5.2 |
| 1.3863 | 1.4351 | 1.4816 | 1.5260 | 1.5686 | 1.6094 | 1.6486 |
Compare it with exact value.
Solution
Let ![]() (1)
(1)
Here ![]()
The interval is (4, 5.2) and it is divided into 6 equal parts with h = 0.2
∴ ![]()
So, we can use Weddle’s rule to find (1).
The points are ![]()
The values of y are y0, y1, y2, y3, y4, y5, y6 and they are given by the table below.

By Weddle’s rule,
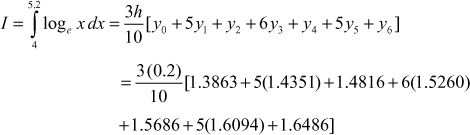

By direct integration,

∴ the actual value is 1.8278
By Weddle’s rule, the value is 1.8278
∴ error is zero.
Example 4
The velocity of the particle at a distance s from a point on its path is given by the table below.
| s (metres) | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| v (m/sec) | 47 | 58 | 64 | 65 | 61 | 52 | 38 |
Estimate the time taken to travel 60 meters by (i) Simpson’s rule
(ii) Simpson’s ![]() rule
rule
(iii) Weddle rule.
Solution
Let s be the distance travelled and v be the velocity at time t.
We know the velocity

∴ the time taken to travel 60 ft is ![]()
The values of y are y0, y1, y2, y3, y4, y5, y6 and they are given by the table below
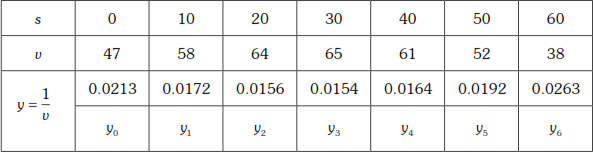
Number of intervals is 6 with h = 10
- Simpson’s
 rule,
rule,


- By Simpson’s
 rule,
rule,
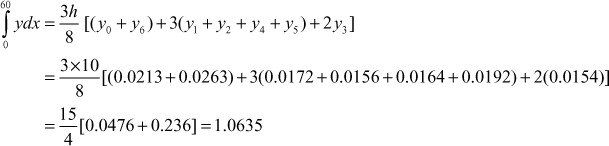
- By Weddle’s rule,
Since n = 6, we can use weddle’s formula.

∴ by the three methods, the time taken to travel the distance is equal, correct to two places of decimal.
7.7 ERROR IN NUMERICAL INTEGRATION FORMULAE
7.7.1 Error in Trapezoidal Rule
Trapezoidal rule is
![]()
where ![]() are the values of
are the values of ![]() at
at ![]()
where ![]() and
and ![]()
Taylor’s series expansion for f (x) about x0 is
![]() (1)
(1)
 (2)
(2)
where ![]()
Area of the trapezium in ![]() is
is ![]()
⇒ ![]() (3)
(3)
 (4)
(4)


∴ The principal part of error in (x0, x1) is ![]()
Similarly principal part of error in (x1, x2) is ![]() etc.
etc.
error in ![]() is
is ![]()
∴ total error E is given by ![]()
If ![]() , then
, then ![]()
Hence the total error in Trapezoidal rule is of order h2
7.7.2 Error in Simpson’s Rule
Simpson’s rule is

where ![]() is even,
is even, ![]() are the values of y = f(x) at
are the values of y = f(x) at ![]()
Taylor’s series expansion of f(x) about x0 is
![]() (1)
(1)
 (2)
(2)
But by Simpson’s rule, area in [x0, x2] is ![]() (3)
(3)
Putting x = x1 in (1), we have
![]()
∴ ![]()
Putting ![]() in (1), we have
in (1), we have
∴ 
Substituting for y1 and y2 in (3) we get
 (4)
(4)
∴ 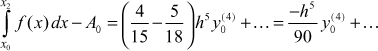
Omitting h6 and higher powers, the principal part of error in ![]() is
is ![]() and so on.
and so on.
the total error ![]()
![]() , where
, where ![]()
∴ ![]()
In the same way, we can find the error in the quadrature formulae. We shall indicate the principal error in each formula
Error in Simpson’s ![]() rule
rule
The principal error in the interval ![]() is
is ![]()
Error in Boole’s rule
The principal error in the interval ![]() is
is ![]()
Error in Weddle’s rule
The principal error in the interval ![]() is
is ![]()
Exercises 7.1
- (1) Evaluate
 using
using
- (i) Trapezoidal rule (ii) Simpson’s
 rule with
rule with 
- (iii) Simpson’s
 rule with
rule with 
- (i) Trapezoidal rule (ii) Simpson’s
- (2) Evaluate
 using the following data.
using the following data.
x 4 4.2 4.4 4.6 4.8 5 5.2 
1.3863 1.4351 1.4816 1.5261 1.5686 1.6094 1.6487 - (i) by Trapezoidal rule (ii) by Simpson’s rule
- (iii) by Simpson’s
 rule
rule
- (3) Using the following table evaluate
 by (a) Trapezoidal rule (b) Simpson’s rule.
by (a) Trapezoidal rule (b) Simpson’s rule.
x 0 0.5 1.0 1.5 2.0 y 0.399 0.352 0.242 0.129 0.054 - (4) Evaluate
 taking i = 0.1 by 9
taking i = 0.1 by 9
- (a) Trapezoidal rule
- Simpson’s rule
- (5) Evaluate
 using
using
- (i) Trapezoidal rule
- Simpson’s rule
- (6) Evaluate
 by
by
- (i) Trapezoidal rule
- Simpson’s rule
- (7) Evaluate
 by Simpson’s rule with h = 0.1.
by Simpson’s rule with h = 0.1. - (8) Evaluate
 using Simpson’s rule with h = 0.25 and hence reduce the value of
using Simpson’s rule with h = 0.25 and hence reduce the value of 
- (9) Evaluate

- Using Simpson’s rule with h = 0.2. Compare the results by integration.
- Evaluate
 by Simpson’s
by Simpson’s  rule.
rule. - Evaluate
 by Simpson’s
by Simpson’s  rule.
rule. - Evaluate
 by Boole’s rule.
by Boole’s rule. - Evaluate
 by Boole’s rule.
by Boole’s rule. - Evaluate
 by Boole’s rule with 13 ordinates.
by Boole’s rule with 13 ordinates. - The following gives the velocity v of a particle at time t..
t in hrs 0 0.25 0.5 0.75 1 1.25 1.5 1.75 2 velocity v km/hr 6 7.5 8 9 8.5 10.5 9.5 7 6 Find the distance travelled in 2 hours.
- Evaluate using Weddle’s rule
- (i)

- (ii)

- (i)
- Evaluate
 by Weddle’s rule with 7 ordinates and reduce the value of loge2.
by Weddle’s rule with 7 ordinates and reduce the value of loge2. - A curve is drawn to pass through the points given by the following table
x 1 1.5 2 2.5 3 3.5 4 y 2 2.4 2.7 2.8 3 2.6 2.1 using Weddle’s rule, estimate the area bounded by the curve, the x-axis and the lines x = 1, x = 4.
Answers 7.1
- 0.7854, 0.7854, 0.7854 (2) 1.82765, 1.82784, 1.82785
- 0.475, 0.477 (4) 0.6686; 0.6321
- 115, 98 (6) 1.4108; 1.3662
- 0.5351 (8) 0.3108
- 4.05214 (10) 1.3571
- 1.3571 (12) 1.8278
- 3.1067 (14) 0.0549
- 0.8236 (16) 16.68 km
- (i) 4.05145 (ii) 0.5051 (18) 0.6932
- 3.032
7.8 ROMBERG’S METHOD FOR INTEGRATION
We have seen different formulae for numerical integration obtained by the finite difference methods. Of the three formulae trapezoidal rule, Simpson’s ![]() rule and Simpson’s
rule and Simpson’s ![]() rule, Simpson’s
rule, Simpson’s ![]() rule gives the best result.
rule gives the best result.
A method due to L.F Richarson known as Richardson’s deferred approach to the limit provides a method to improve the accuracy of the approximate values of definite integrals obtained by finite difference methods. This technique is known as Romberg’s integration.
7.8.1 Romberg’s Integration Formula Based on Trapezoidal Rule
Let ![]()
Let I1, I2 be two values of I by trapezoidal rule with subintervals of width h1, h2 and let E1, E2 be their corresponding errors. Let ![]()
Then ![]()
and ![]()
Since ![]()
![]() are both largest values of
are both largest values of ![]() we can assume
we can assume ![]() and
and ![]() are nearly equal.
are nearly equal.
![]()
But I = I1 + E1 and also I = I2 + E2

which is a better approximation of I than I1 and I2.
This method is called Richardson’s deferred approach to the limit.
To evaluate I systematically, we take ![]()
 (1)
(1)
This is known as Romberg’s formula.
The formula (1) is obtained by trapezoidal rule twice with width of intervals h and ![]()
We again apply trapezoidal rule with width ![]() and apply several times halving the intervals. Each time the error is reduced by a factor
and apply several times halving the intervals. Each time the error is reduced by a factor ![]()
Thus we have a sequence of values of I.
I1, I2, I3, I4, ... are the values with width ![]()
Applying (1) for the pairs I1, I2; I2, I3; I3, I4; ... , we get A1, A2, A3, … . which are improved values.
Again applying (1) to the pairs
We get ![]()
This systematic refinement of Richardson’s method is called Romberg method or Romberg integration.
WORKED EXAMPLES
Example 1
Evaluate ![]() correct to 3 places using Romberg’s method and hence find the value of loge 2.
correct to 3 places using Romberg’s method and hence find the value of loge 2.
Solution
Let ![]()
Here ![]()
Trapezoidal rule is

We shall find the value of the integral when h = 0.5, 0.25, 0.125
When h = 0.5, the values of y are given by the table below

![]()
When ![]() the values of y are given by the table below
the values of y are given by the table below


When ![]() the values of y are given by the table below
the values of y are given by the table below


We shall now use Romberg’s formula for I1, I2

Again for I2 and I3, we have

Now again applying Romberg’s method with ![]()

By direct integration,
∴ 
Note: We find using calculator loge 2 = 0.69314718.
So, the answer by Romberg’s method is correct to 4 decimal places.
Example 2
Evaluate ![]() by using Romberg’s method correct to 4 decimal places. Hence deduce an approximate value of p.
by using Romberg’s method correct to 4 decimal places. Hence deduce an approximate value of p.
Solution
Let ![]()
Here ![]()
Trapezoidal rule is ![]()
We shall find the value of I by trapezoidal rule for h = 0.5, 0.25, and 0.125
When h = 0.5, then the values of y are given by the table below

Then ![]()
When ![]() the values of y are given by the table below
the values of y are given by the table below

Then

When ![]() the values of y are given by the table below.
the values of y are given by the table below.

Then

We shall now use Romberg’s formula ![]() for the pairs I1, I2.
for the pairs I1, I2.
∴ ![]()
and for the pair I2, I3

So, for 4 decimals the 2 improvements coincide.
∴ the value of I = 0.7854
∴ ![]()
By direct integration, ![]()
![]()
Note: From calculator ![]() = 3.141592654.
= 3.141592654.
So, the value is correct to 4 places.
Example 3
Evaluate ![]() using Romberg’s formula.
using Romberg’s formula.
Solution
Let 
Let ![]()
Trapezoidal rule is 
![]()
We shall find the values of the integral when ![]()
When ![]() the values of y are given by the table below
the values of y are given by the table below


When ![]() the values of y are given by the table below.
the values of y are given by the table below.


When ![]() the values of y are given by the table below.
the values of y are given by the table below.


Applying Romberg’s formula for the pairs ![]() and
and ![]() , We get
, We get

Again for the pairs I2, I3, we get
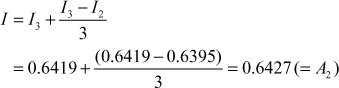
Again applying Romberg’s formula for ![]() we get
we get

∴ 
Note: By direct integration


So, we find that the value by Romberg’s method is correct.
Example 4
Evaluate ![]() using Romberg’s method.
using Romberg’s method.
Solution
Let ![]()
Here ![]()
Trapezoidal rule is
![]()
When ![]() , we shall find the values of the integral.
, we shall find the values of the integral.
When ![]() the values of y are given by the table below.
the values of y are given by the table below.


When ![]() the values of y are given by the table below.
the values of y are given by the table below.


When ![]() the values of y are given by the table below
the values of y are given by the table below


![]()
We shall now use Romberg’s formula for ![]()
![]()

Again applying Romberg’s method with ![]() we get
we get
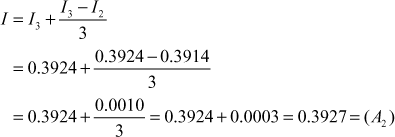
Since ![]() upto 4 places of decimals.
upto 4 places of decimals.
We shall take I = 0.3927
Note:
By direct integration 
So, we find that the value by Romberg’s method is correct.
7.8.2 Romberg Integration Formula Based on Simpson’s Rule
Let ![]() .
.
Let ![]() be two values of I by Simpson’s
be two values of I by Simpson’s ![]() rule with sub-intervals width
rule with sub-intervals width ![]() and let
and let ![]() be their corresponding errors.
be their corresponding errors.
Then ![]()
and ![]()
where ![]() and
and ![]() are largest values of
are largest values of ![]() ,
,
We assume them to be nearly equal.
![]()
Suppose ![]() and
and ![]() then
then 
But ![]()
 (1)
(1)
This is Romberg’s formula using Simpson’s rule.
Again applying Simpson’s rule with ![]() , we get a sequence of values of I.
, we get a sequence of values of I.
Let ![]() be the values of the integral with width
be the values of the integral with width ![]()
Applying the formula (1) for the pairs ![]()
we get ![]() which are improved values of I.
which are improved values of I.
Again applying (1) to the pairs ![]()
we get ![]() which are still improved values.
which are still improved values.
This method is called Romberg’s method.
WORKED EXAMPLES
Example 1
Find the value of  correct to 4 decimal places using Simpson’s rule and Romberg’s integration.
correct to 4 decimal places using Simpson’s rule and Romberg’s integration.
Solution
Let 
Here ![]()
Simpson’s ![]() rule is
rule is
![]()
where n is even
We shall find the values of the integral with ![]()
When h = 0.5, number of intervals is 2 ∴ n = 2
Since ![]() the values of y are given by the table below.
the values of y are given by the table below.

Simpson’s formula is
∴ 
When h = 0.25, n = 4, even
The values of y are given by the table below.


When h = 0.125, n = 8, even
The values of y are given by the table below.


We now use Romberg’s formula for the pairs ![]() and
and ![]()

Also 
Since ![]() upto five places of decimals, we take
upto five places of decimals, we take
![]()
So, the value I,corrected to 4 places of decimal is 1.9461.
Example 2
A certain curve is given by the following points
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 0.2 | 0.7 | 1 | 1.3 | 1.5 | 1.7 | 1.9 | 2.1 | 2.3 |
Using Simpson’s rule and Romberg’s formula, find the volume generated by revolving the area bounded by this curve, the x-axis and the ordinates x = 1 and x = 9 about the x-axis.
Solution
Required volume I ![]()
Let us evaluate this integral by Simpson’s rule with h = 4, 2, 1
When h = 4, n = 2, even. The values of ![]() are given by the table below.
are given by the table below.

By Simpson’s formula,
∴ 
When ![]() even
even
The values of ![]() are given by the table below.
are given by the table below.

By Simpson’s formula,
∴ 
When ![]() , even
, even
The values of y2 are given by the table below.
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 0.2 | 0.7 | 1 | 1.3 | 1.5 | 1.7 | 1.9 | 2.1 | 2.3 |
| 0.04 | 0.49 | 1 | 1.69 | 2.25 | 2.89 | 3.61 | 4.41 | 5.29 | |
By Simpson’s formula,
∴ 
Applying Romberg’s formula for the pairs ![]() and
and ![]() we get
we get
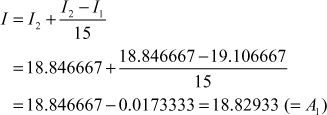
Also

![]()
Applying Romberg’s formula for ![]()

∴ p × I
![]()
Example 3
Evaluate ![]() using Simpson’s rule and Romberg’s method.
using Simpson’s rule and Romberg’s method.
Solution
Let ![]()
Here ![]()
Simpson’s rule is

Let us evaluate the integral with ![]()
When ![]() , even
, even
The values of y are given by
| x | 0 | 1 | 2 |
| 0 | 1 | 4 | |
| 0.25 | 0.2 | 0.125 | |
By Simpson’s rule,
∴ 
When ![]() , even
, even
The values of y are given by the table below.
| x | 0 | 1 | 2 | ||
| 0 | 0.25 | 1 | 2.25 | 4 | |
| 0.25 | 0.2353 | 0.2 | 0.16 | 0.125 | |
By Simpson’s rule,
∴ 
When ![]() , even
, even
The values of y are given by the table below.
| x | 0 | 0.25 | 0.5 | 0.75 | 1 | 1.25 | 1.5 | 1.75 | 2 |
| 0.25 | 0.2462 | 0.2353 | 0.2192 | 0.2 | 0.1798 | 0.16 | 0.1416 | 0.125 | |
By Simpson’s rule,
∴ 
Now we use Romberg’s formula for the pairs ![]() and
and ![]() .
.

Also

Now applying Romberg’s formula with ![]() and
and ![]() , we get
, we get
∴ 
7.9 TWO AND THREE POINT GAUSSIAN QUADRATURE FORMULAE
7.9.0 Introduction
To evaluate the integral  we have developed various approximate formulae, namely trapezoidal rule, Simpson’s
we have developed various approximate formulae, namely trapezoidal rule, Simpson’s ![]() rule and Simpson’s
rule and Simpson’s ![]() rule. In these formulae we used the values of the function
rule. In these formulae we used the values of the function ![]() at equally spaced values of argument x. Here the values of x are predetermined. Gaussian quadrature formula uses the same number of values of
at equally spaced values of argument x. Here the values of x are predetermined. Gaussian quadrature formula uses the same number of values of ![]() but the values of x are not equally spaced and choosing the points suitably we can find an improved estimate of the integral.
but the values of x are not equally spaced and choosing the points suitably we can find an improved estimate of the integral.
Any finite interval [a, b] can be transformed into [–1, 1] by the transformation ![]()

and 
So, we consider the integral in the form 
The general n-point Gaussian quadrature formula assumes an approximation of the form
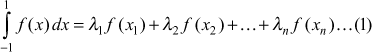 , where
, where ![]() are the points of division of the interval [–1, 1], which are known as nodes and
are the points of division of the interval [–1, 1], which are known as nodes and ![]() are known as the weights. Since there are 2n unknowns in the relation (1), 2n relations between the variables
are known as the weights. Since there are 2n unknowns in the relation (1), 2n relations between the variables ![]() are necessary and the formula is exact for polynomials of degree
are necessary and the formula is exact for polynomials of degree ![]() Formulae based on this idea are called Gaussian quadrature formulae.
Formulae based on this idea are called Gaussian quadrature formulae.
This method is applicable only when f(x) is known explicitly so that the values of the function can be evaluated at any given value of x.
The quadrature formula is derived assuming ![]() are the roots of the equation
are the roots of the equation ![]() , where
, where ![]() is the Legendre polynomial of degree n given by Rodrigue’s formula
is the Legendre polynomial of degree n given by Rodrigue’s formula
![]()
We also assume ![]() can be expanded as a power series of degree
can be expanded as a power series of degree ![]() in
in ![]() so that
so that
![]()
We shall derive the quadrature formulae when n = 2 and n = 3 which are called the two point quadrature formula and three point quadrature formula respectively.
7.9.1 Two Point Gaussian Quadrature Formula
When n = 2, the two point quadrature formula is
 (1)
(1)
Where x1 and x2 are the roots of P2 (x) = 0

Since ![]() . So
. So ![]() is a polynomial of degree 3.
is a polynomial of degree 3.
Let ![]()


∴ Equating like coefficients we get
![]()
The two point quadrature formula is

Note: It is also known as two point Gauss-Legendre formula. It gives good estimate with two functional values.
7.9.2 Three Point Gaussian Quadrature Formula
The three point formula is
 (1)
(1)
where x1, x2, x3 are roots of P3 (x) = 0, where P3 (x) is the Legendre polynomial of degree 3.

Let ![]()
To find ![]() , we assume f(x) is a polynomial of degree 5, since
, we assume f(x) is a polynomial of degree 5, since ![]()
Let ![]()

Equating like coefficients, we get
![]() (2)
(2)
![]() (3)
(3)

![]()
Substitute in (2), we get

WORKED EXAMPLES
Example 1
Apply Gauss two-point formula to evaluate ![]() .
.
Solution
Let 
We know  since
since ![]() is even function of x
is even function of x
∴ 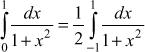 . Here
. Here ![]()
Gauss two-point formula is

Example 2
Evaluate ![]() by 2-point Gaussian formula.
by 2-point Gaussian formula.
Solution
Let 
First transform the interval ![]() into the interval [–1, 1]
into the interval [–1, 1]
For. this, put ![]() Here
Here ![]()
![]() ∴
∴ ![]() ∴ <Eqn Eqn1263"/> ∴
∴ <Eqn Eqn1263"/> ∴ ![]()
When ![]() and when
and when ![]()

By 2-point Gaussian formula,

But 
![]()
∴ 
Example 3
Using three point Gaussian formula, evaluate ![]() .
.
Solution
Let 
We have to transform the interval [0.2, 1.5] into the interval [–1, 1]
For this, Put ![]() . Here
. Here ![]()
![]()
When ![]() and when
and when ![]()

Here ![]()
Three point quadrature formula is
But 
∴ 

∴ 
Example 4
Evaluate ![]() using 3-point Gauss quadrature formula and compare with the actual value.
using 3-point Gauss quadrature formula and compare with the actual value.
Solution
Given 
We have to transform the interval [1, 2] into [–1, 1]
For this, Put ![]() . Here a = 1, b = 2
. Here a = 1, b = 2
![]() ∴
∴ ![]()
![]()
When ![]()

We know 3-point Gaussian formula is

But 

We shall now find the exact value by integration.

Put ![]()
When ![]() and when
and when ![]()

The error is 0.5408 − 0.5404 = 0.0004
Example 5
Evaluate ![]() dx by three point Gaussian formula.
dx by three point Gaussian formula.
Solution
Let  dx
dx
First transform the interval [0, 2] into the interval [–1, 1]


But

Example 6
Evaluate ![]() using Gaussian (i) two points formula (ii) three point formula.
using Gaussian (i) two points formula (ii) three point formula.
Solution
Given  .
.
Here ![]()
- (i) Gaussian two point formula is

- (ii) Gaussian three point formula is


Note: We shall now find the actual value by integration.

∴ Error in 2 point formula = |1.5708 – 1.5| = 0.0708
Error in 3 point formula = |1.5708 – 1.5833| = 0.0125
So the error in 3-point formula is less than the error in 2-point formula.
Example 7
Obtain ![]() by using Gauss two point and three point rules.
by using Gauss two point and three point rules.
Solution
Let 
Transform the interval [2, 3] into [–1, 1] by the transformation

When ![]() and when
and when ![]()
∴ 
∴ 
- Two point Gaussian formula is

Now

∴

- The three point Gaussian formula is
∴

Example 8
Using Gaussian two and three point formulae evaluate ![]() .
.
Solution
Given 
First we transform the interval [2, 3] into the interval [–1, 1]
For this, put 
When ![]() and when
and when ![]()

- (i) Two point Gaussian formula is


- (ii) Three point Gaussian formula is

Now

∴
Exercises 7.2
- Evaluate
 by Romberg’s method with h = 0.1 and h = 0.2 and using Trapezoidalrule.
by Romberg’s method with h = 0.1 and h = 0.2 and using Trapezoidalrule. - Evaluate
 by using Romberg’s method taking
by using Romberg’s method taking 
- Calculate
 using trapezoidal rule with
using trapezoidal rule with  and then Romberg’s formula.
and then Romberg’s formula. - From the following data evaluate
 using Romberg’s method with h=0.8, 0.4
using Romberg’s method with h=0.8, 0.4
x 1.8 2 2.2 2.4 2.6 2.8 3 3.2 3.4 f(x) 6.050 7.389 9.025 11.023 13.464 16.445 20.086 24.533 29.964 - Evaluate
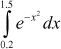 with h = 0.65, 0.325 by Romberg’s method.
with h = 0.65, 0.325 by Romberg’s method. - Evaluate
 by two point Gaussian formula.
by two point Gaussian formula. - Evaluate
 using two point Gaussian formula.
using two point Gaussian formula. - Evaluate
 by using three point Gaussian formula. Compare with actual value.
by using three point Gaussian formula. Compare with actual value. - Evaluate
 using 3-point Gaussian formula.
using 3-point Gaussian formula. - Evaluate
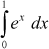 using three point Gaussian formula.
using three point Gaussian formula. - Evaluate
 using two point and three point Gaussian formula.
using two point and three point Gaussian formula.
Answers 7.2
(1) 1.8521 (2) 0.3927 (3) 0.507070
(4) 23.9181 (5) 0.6586 (6) 4.6854
(7) 1.5432, 1.3911 (8) 4 (9) 1.3247
(12) 1.7128 (11) 0.9985
7.10 EULER-MACLAURIN FORMULA FOR NUMERICAL INTEGRATION
Euler-Maclaurin’s formula for integration is

Where ![]() and
and ![]()
Derivation: Let ![]()
Divide the interval ![]() into n equal intervals of width
into n equal intervals of width ![]()
![]()
Let
∴ 
Adding all these equations, we get
![]() (1)
(1)
Since ![]() , we define the inverse operator
, we define the inverse operator ![]() as
as





∴  (2)
(2)
Putting ![]() and
and ![]() in (2), we get
in (2), we get
![]() (3)
(3)
![]() (4)
(4)


Substituting for L.H.S. from (1), we get



This is called Euler-Maclaurin’s formula for integration.
Incase higher derivatives are involved, then the formula is
∴ 
Note: This formula can be rewritten as

This is called Euler-Maclaurin’s formula for summation.
WORKED EXAMPLES
Example 1
Evaluate ![]() by Euler-Maclaurin formula for integration. Hence find the value of p and compare with the correct value upto 5 decimals.
by Euler-Maclaurin formula for integration. Hence find the value of p and compare with the correct value upto 5 decimals.
Solution
Let ![]()
Here ![]()
Euler-Maclaurin formula for integration is
∴  (1)
(1)
where n = the number of sub-intervals and ![]()
Let ![]()
The values of x are ![]() ,
, ![]()
![]()
The values of ![]() are given by the table below.
are given by the table below.
| x | |||||||
| 0 | 1 | ||||||
| 1 | 0.97297 | 0.9 | 0.8 | 0.69231 | 0.59016 | 0.5 | |
∴ We have 

∴ 
∴ 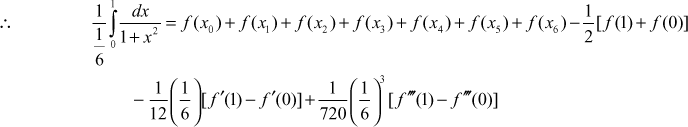
∴ 
![]()
But ![]()
Using Calculator 
∴ Euler-Maclaurin method gives correct answer upto 5 places of decimal.
Example 2
Find by Euler’s quadrature formula, the value of the integral ![]() .
.
Solution
Let ![]()
Here ![]()
Euler-Maclaurin’s formula for integration is

where n = the number of sub-intervals and ![]() .
.
Let ![]()
The values of x are ![]()
The values of ![]() are given by table below
are given by table below
| x | ||||||
| 0 | 1 | |||||
| 1 | 0.99920 | 0.98723 | 0.93590 | 0.8021 | 0.54030 | |
We have
∴ 
∴ ![]()

∴ 
∴ 
∴ ![]()
Example 3
Applying Euler-Maclaurin summation formula, evaluate
![]()
Solution
Required the sum of ![]()
Here ![]()
By Euler – Maclaurin formula for summation

We have
∴ 
and ![]()

∴ 

Example 4
By Euler’s formula prove that the sum of the cubes of the first n natural numbers is ![]() .
.
Solution
We have to prove ![]()
![]()
Here ![]()
By Euler’s formula for summation
![]()
We have ![]()
∴ ![]()

∴ 
7.10.1 Application of Euler-Maclaurin Formula
Stirling’s approximation for factorial
If n is a positive integer, then we know, ![]()
∴  (1)
(1)
We shall find the sum by Maclaurin’s formula.
Here 
Maclaurin’s formula for summation is
∴ 
![]() (2)
(2)
To find C, we use Weddle’s formula, namely
![]()
Taking logarithm, we get
∴ ![]()
As ![]()
∴![]() approximately (from (1) and (2))
approximately (from (1) and (2))
∴

![]()
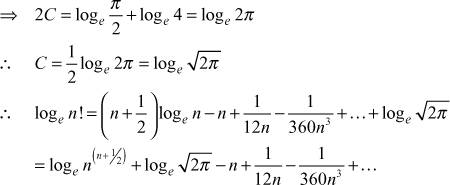


Corollary: When n is large ![]() are very small and so can be neglected
are very small and so can be neglected
![]()
WORKED EXAMPLES
Example 1
Calculate ![]() correct to six places of decimals and hence find the number of digits in 81!
correct to six places of decimals and hence find the number of digits in 81!
Solution
Stirling’s formula for n! is ![]()
Taking log to the base 10,

Put n = 81, we get
∴ 
Since the integer part is 120, the number of digits in 81! is 121
Example 2
Using Stirling’s approximation for n!, find the number of digits in the value of 100C50.
Solution
Let ![]()
Taking log to the base 10, we get
![]()
Stirlings formula for n! is
![]()
∴  (1)
(1)
Put n = 100 in (1), then

Now put n = 50 in (1), then

![]()
∴ x = anti log (29.0039)
Since the integral part is 29, the number of digits in 100C50 is 30
Exercises 7.3
(I) Evaluate the following integrals using Euler-Maclaurin formula.
 correct to fine decimal places.
correct to fine decimal places. correct to seven decimal places.
correct to seven decimal places. correct to five decimal places.
correct to five decimal places. and hence find the values of p.
and hence find the values of p.
(II) Evaluate the following sums.
 correct to 6 decimals.
correct to 6 decimals.
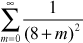 correct to 6 places of decimals.
correct to 6 places of decimals.

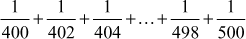

- Find the sum of the fourth powers of first n natural numbers.
(III) Using Stirling approximation for factorials, compute to six places of decimals
Answers 7.3
(I)
- 2.40011
- 0.0487902
- 0.69315
- 0.7854, π = 3.1416
(II)
- 0.6956534
- 0.0049998
- 0.133137
- 0.0049988
- 0.144539
- 0.11382
- (7) 0.0008333
(III)
- 98.233911
- 615.5999
- 28.138179
- 2567.59914
7.11 DOUBLE INTEGRATION
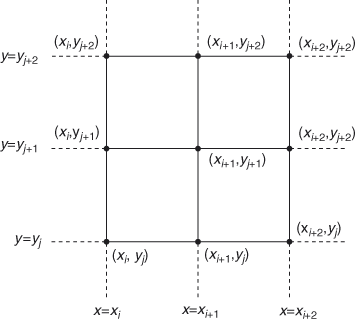
We shall now consider the numerical evaluation of a definite double integral of a function of two independent variables from a set of numerical values of the integrand. The process of computation of double integral of a function of two independent variables is called mechanical cubature.
We have seen in calculus that a double integral ![]() with constant limits can be evaluated by integrating w.r.to x first treating y as constant and then integrating w.r.to y. So we can evaluate a double integral by applying trapezoidal rule or Simpson’s rule repeatedly.
with constant limits can be evaluated by integrating w.r.to x first treating y as constant and then integrating w.r.to y. So we can evaluate a double integral by applying trapezoidal rule or Simpson’s rule repeatedly.
7.11.1 Trapezoidal Rule for Double Integral
Let![]() . The region of integration is the rectangle bounded by
. The region of integration is the rectangle bounded by
the lines x = a, x = b, y = c, y = d in the xy plane.
Divide the interval [a, b] into n equal subintervals of width h at the points
![]()
![]()
and the interval [c, d] into m equal subintervals of width k at the points
![]()
![]()
![]()
Let

Consider the typical rectangle ABIH over which we shall evaluate the integral


By trapezoidal rule for the inner integral with two values, we get

Again applying trapezoidal rule
 (1)
(1)
To evaluate  , we have to evaluate over the rectangle ACEG, which is the sum of four rectangles.
, we have to evaluate over the rectangle ACEG, which is the sum of four rectangles.
∴ 
Using (1) to each of these integrals, we get



More generally, the value of the double integral is

WORKED EXAMPLES
Example 1
Evaluate ![]() by Trapezoidal rule for the following data:
by Trapezoidal rule for the following data:

Solution
Let ![]()
The given values of x are equally spaced with h = 0.5
The given values of y are equally spaced with k = 1

∴ the Trapezoidal rule for double integral is

The corner values are squared.
Other boundary values are indicated by arrows.
The interior values are inside the dotted curve.

Example 2
Use trapezoidal rule to evaluate  taking 4 subintervals.
taking 4 subintervals.
Solution
Let ![]()
Here ![]()
Number of subintervals is 4. ![]()
∴ the values of x are 1, 1.25, 1.5, 1.75, 2 and the values of y are 1, 1.25, 1.5, 1.75, 2
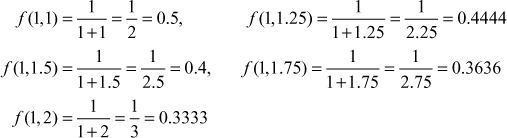
Similarly


Now we tabulate the values of ![]()

∴ the trapezoidal rule for double integral is

The corner values are squared. Boundary values are indicated by arrows. Interior values are inside the dotted curve.

Example 3
Evaluate ![]() by Trapezoidal rule.
by Trapezoidal rule.
Solution
Let ![]()
Here ![]()
We shall take h = 0.5, k = 0.25
∴ the values of x are 0, 0.5, 1 and the values of y are 0, 0.25, 0.5, 0.75, 1.
∴ 
Similarly

Now we shall tabulate the values of f(x, y)

∴ the Trapezoidal rule for double integral is
![]() [sum of the corner values
[sum of the corner values
+ 2 (sum of other values of ![]() on the boundary)
on the boundary)
+ 4 (sum of the interior values of![]() ]
]
The corner values are squared.
Other boundary values are indicated by arrows.
The interior values are inside the dotted curve.

Note: The exact value of this double integral is ![]() .
.
So, the error is 0.0087
Example 4
Evaluate ![]() by Trapezoidal rule with h = k = 0.25.
by Trapezoidal rule with h = k = 0.25.
Solution
Let ![]()
Here ![]()
∴ the values of x are 1, 1.25, 1.5, 1.75, 2
and the values of y are 0, 0.25, 0.5, 0.75, 1

Similarly

Now we shall tabulate the value of ![]()

∴ the Trapezoidal rule for double integration is
![]() [sum of the corner values
[sum of the corner values
+ 2 (sum of the other values of ![]() on the boundary)
on the boundary)
+ 4 (sum of the interior values of ![]() ]
]
The corner values are squared.
Other values of f(x, y) on the boundary are indicated by arrows.
The interior values are inside the dotted curve.
∴ 
Example 5
Evaluate ![]() using Trapezoidal rule with h = k = 0.5 and h = k = 0.25. Improve the estimate by Romberg’s formula.
using Trapezoidal rule with h = k = 0.5 and h = k = 0.25. Improve the estimate by Romberg’s formula.
Solution
Let ![]()
Here ![]()
Case (i) h = k = 0.5
The values of x are 1, 1.5, 2 and the values of y are 1, 1.5, 2

Similarly

We shall tabulate the values of ![]()

Trapezoidal rule for double integration is


Case (ii) h = k = 0.25
By worked example 2 page . . . I = 0.3401
Taking the estimates as I1 = 0.3433 and I2 = 0.3401
By Romberg’s formula 
7.11.2 Simpson’s Rule for Double Integral
Let ![]()
We divide [a, b] into an even number of intervals 2n and [c, d] is divided into an even number of intervals 2m.
Applying Simpson’s rule taking 2 intervals in the x-direction and 2 intervals in the y-direction.
Let ![]()
The points of division are
∴ 
The typical sub-rectangles are taken with 2 intervals in x-direction and 2 intervals in y-direction.
Consider 
By applying Simpson’s rule in the x-direction, for 2 intervals keeping y-constant to the inner integral we get

Again apply Simpson’s rule to each integral in the y-direction.


This can be extended if the number of intervals is 4 or 6 in each direction applying for every pair of intervals.
WORKED EXAMPLES
Example 6
Evaluate ![]() using Trapezoidal rule and Simpson’s rule.
using Trapezoidal rule and Simpson’s rule.
Solution
Let ![]()
Here ![]()
We shall take h = 0.5, k = 0.5 and thus dividing into 2 intervals each.
∴ the value of x are 0, 0.5, 1 and the values of y are 0, 0.5, 1
∴ 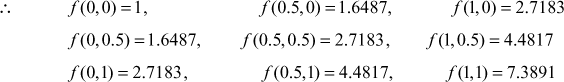
We shall tabulate the values

- (i) Trapezoidal rule for double integral is


- (ii) Simpson’s rule for double integral is


Note: Integrating we get the actual value 2.9525 correct to 4 decimals So we notice that the value of Simpson’s rule is very close to the actual value.
Example 7
Using Simpson’s ![]() rule evaluate
rule evaluate ![]() by taking h = k = 0.5.
by taking h = k = 0.5.
Solution
Let ![]()
Here ![]()
Given ![]()
∴ the values of x are 0, 0.5, 1 and the values of y are 0, 0.5, 1.
So the interval is divided into 2 parts.
![]()

We shall tabulate the value
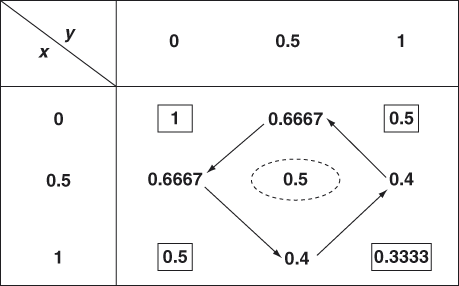
Simpson’s rule for double integral is


Note: By integration the actual value is 0.5232 upto 4 places.
Example 8
Evaluate ![]() by Simpson’s rule with h = k = 0.25.
by Simpson’s rule with h = k = 0.25.
Solution
Let ![]()
Here ![]() and h = k = 0.25
and h = k = 0.25
∴ the values of x are 0, 0.25, 0.5 and the values of y are 0, 0.25, 0.5
So the interval is divided into 2 parts.

Similarly,

We shall tabulate the values of f (x, y)

Simpson’s rule of double integral is


Example 9
Evaluate ![]() using Simpson rule, given h = k = 0.1.
using Simpson rule, given h = k = 0.1.
Solution
![]()
Here ![]()
Given h = 0.1, k = 0.1
∴ the values of x are 4, 4.1, 4.2, 4.3, 4.4 and the values of y are 2, 2.1, 2.2, 2,3, 2.4
The interval is divided into 4 sub intervals.
Similarly,
f(4.1,2) = 8.2, f(4.1,2.1) = 8.61, f(4.1,2.2) = 9.02,
f(4.1,2.3) = 9.43, f(4.1,2.4) = 9.84,
f(4.2,2) = 8.4, f(4.2,2.1) = 8.82, f(4.2,2.2) = 9.24,
f(4.2,2.3) = 9.66, f(4.2,2.4) = 10.08,
f(4.3,2) = 8.6, f(4.3,2.1) = 9.02, f(4.3,2.2) = 9.46,
f(4.3,2.3) = 9.89, f(4.3,2.4) = 10.12,
f(4.4,2) = 8.8, f(4.4,2.1) = 9.24, f(4.4,2.2) = 9.68,
f(4.4,2.3) = 10.12, f(4.4,2.4) = 10.56
We shall formulate the table value of ![]()

We shall rewrite the integral as sum of 4 integrals taking 2 intervals at a time and apply Simpson’s rule
where
∴ 
Using Simpson’s rule for 2 intervals


∴ 

∴ ![]()

Note: Directly integrating we get the exact value as 1.4784. So in this problem Simpson’s formula gives the exact value.
Example 10
Evaluate ![]() by Simpson’s rule for double integration.
by Simpson’s rule for double integration.
Solution
Let ![]()
Here ![]()
Let ![]() and
and ![]()
The order of integration is first w.r.to y and then w.r.to x.
The values of x are 4, 4.3, 4.6, 4.9, 5.2 and the value of y are 2, 2.3, 2.6, 2.9, 3.2
The interval is divided into 4 sub-intervals.


We shall tabulate the values of ![]()

We shall rewrite the given integral as the sum of four integrals taking two intervals at a time and applying Simpson’s rule
∴
Now

∴
∴
and
∴
∴ ![]()
Aliter: We shall apply Simpson’s rule to the rows, treating the values 2, 2.3, 2.6, 2.9 and 3.2 as x values and the function values of I row as ![]()
Applying for I row, we get the following table:
| x | 2 | 2.3 | 2.6 | 2.9 | 3.2 |
| y |
∴ 
Applying for II row, we get the following table.
| x | 2 | 2.3 | 2.6 | 2.9 | 3.2 |
| y |

Similarly applying Simpson’s rule for III and IV and V rows, we get



Now treating 4, 4.3, 4.6, 4.9, 5.2 as x values and ![]() as y values and applying Simpson’s rule we get
as y values and applying Simpson’s rule we get

Note: By direct integration the actual value of the integral is


Error = 0.123312 – 0.123316 = 0.000004, which is negligible.
Exercises 7.4
- Evaluate
 using trapezoidal rule taking h = 0.1 and k = 0.8.
using trapezoidal rule taking h = 0.1 and k = 0.8. - Evaluate
 using trapezoidal rule with 4 subintervals.
using trapezoidal rule with 4 subintervals. - Evaluate
 using trapezoidal rule with 4 subintervals.
using trapezoidal rule with 4 subintervals. - Apply Simpson’s rule to evaluate
 by taking h = 0.2, k = 03.
by taking h = 0.2, k = 03. - Evaluate
 taking h = k = 0.5 by Simpson’s rule.
taking h = k = 0.5 by Simpson’s rule. - Evaluate
 using Simpson’s rule by taking
using Simpson’s rule by taking  . Also find by trapezoidal rule.
. Also find by trapezoidal rule. - Evaluate
 using Simpson’s rule with
using Simpson’s rule with 
- Evaluate
 using
using - (i) Trapezoidal rule and (ii) Simpson’s rule with

Answers 7.4
(1) 0.0429 (2) 3.9975 (3) 0.0614
(4) 0.025 (5) 0.0408 (6) 2.0095, 1.7976
(7) 2.1546 (8) (i) –1.7976 (ii) –2.0091
Short Answer Questions
- Evaluate
 by Trapezoidal rule, dividing the range into 4 equal parts.
by Trapezoidal rule, dividing the range into 4 equal parts. - When does Simpson’s rule give exact result?
- Write down trapezoidal rule to evaluate
 with h = 0.5, function f(x) is unknown.
with h = 0.5, function f(x) is unknown. - In order to evaluate
 by trapezoidal rule and by Simpson’s rule, what is the restriction on the number of intervals?
by trapezoidal rule and by Simpson’s rule, what is the restriction on the number of intervals? - What are the errors in trapezoidal and Simpson’s rules of numerical integration?
- What is the order of error in Simpson’s
 rule?
rule? - State the local error term in Simpson’s
 rule.
rule. - State Newton’s formula to find
 using the forward differences.
using the forward differences. - What is the order of the error in trapezoidal rule?
- Why is trapezoidal rule so called?
- Write down Simpson’s
 rule, assuming 3n intervals.
rule, assuming 3n intervals. - What are the truncation errors in Trapezoidal rule and Simspon’s
 rule?
rule? - Evaluate
 using trapezoidal rule by taking
using trapezoidal rule by taking 
- Using two point Gaussian quadrature formula, evaluate
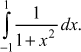
- Evaluate
 using Gaussian quadrative with 2 points.
using Gaussian quadrative with 2 points. - State Romberg’s integration formula to find the value of
 using
using 
