Chapter 7

Planning Capacity

In This Chapter

Determining the correct capacity level for your business

Analyzing supply and demand to balance capacity and inventory

Estimating and adjusting wait time

In a perfect world, output would be designed to exactly meet steady demand at a low cost. However, demand variability is an unfortunate business reality, and operations managers have a number of ways to manage fluctuations. One of the most important is adjusting the output rate, or capacity.

Capacity is a company’s maximum possible sustained level of output of goods or services. Part I of this book goes into detail about how to calculate and utilize process capacity. In this chapter, we take a closer look at capacity, focusing on how to leverage capacity by long-term planning (including appointment and reservation policies) to achieve company goals, such as maximizing profit. We also describe a process for determining how much capacity you really need. After all, more capacity costs more money, and a company doesn’t want to build any more than it really needs. We also address how you can use inventory to reduce the need for capacity over the long term. Finally, we look at how capacity influences the issue of customer lines and wait times, which is a common issue in many service and some manufacturing industries.

This chapter is primarily meant to help you perform long-term capacity planning. After you determine capacity to match long-term demand trends, you need other techniques to help manage short-term fluctuations in demand. In Chapter 8, we cover inventory management, and in Chapter 9, we look at short-term aggregate demand planning. In many firms, different individuals perform each of these functions, yet each of these methods has a part to play in meeting variable demand.

Considering Capacity

No simple standard equation exists to tell you how much capacity you need — right now or in the future — or when exactly you should add capacity. Determining the correct capacity level for your business at any given time to satisfy customer demand takes a great deal of assessment and careful consideration because demand fluctuates, and adding capacity (which often involves building facilities, securing suppliers, and/or training employees) takes time and money.

When developing a capacity plan, start by answering these questions:

How variable is your customer demand? When demand is smooth, operations are pretty simple. Unfortunately, however, demand tends to have a great deal of variability. The more variable your demand is over time, the more capacity and/or inventory you need in order to cover demand during the spikes. (In Chapter 9, find out how to smooth out the spikes with aggregate planning.)

How much inventory can you hold? Answering this question requires you to understand the costs of holding inventory (see Chapter 8) and how time spent in inventory affects product quality (covered in Chapters 12 and 13). If your product is tiramisu, for example, the cake’s quality may deteriorate as it sits in the freezer.

How expensive is acquiring and maintaining capacity? Getting a handle on your how much your capacity costs to acquire and maintain is important because you need to know how much it costs to maintain extra capacity to deal with surges in demand. (We cover the costs of capacity in Chapter 5.)

How long is your customer willing to wait for your product or service? You must know your customer’s expectations when it comes to delivery lead time, or how long a customer must wait between placing the order and receiving the product. For service industries, this equals time spent waiting in line for service. Wait time is an important component of customer satisfaction.

How long does it take to expand or build new capacity? If you have to hire people or buy equipment, expanding capacity may take a long time and require careful planning, as covered in this chapter. On the other hand, you may be able to cover small increases with overtime (see Chapter 9) or temporary increases with short-run inventory buildups, as described in the later Balancing Capacity and Inventory section. These topics are also covered in Chapter 9.

Matching supply and demand

Managing demand variability creates a perplexing problem for managers seeking to improve the return on investment (ROI) of their operation. Building and maintaining capacity (along with producing and holding inventory) is expensive; capacity and inventory represent a huge portion if not most of the costs associated with doing business. On the other hand, if you don’t have the capacity or inventory you need to manage demand variability, you risk late shipments or not having product available when customers want it. So you can either spend money on extra capacity and/or inventory to meet demand surges or risk losing customer revenue.

Predicting demand, particularly over the long term, is difficult. Using the forecasting methods described in Chapter 6, you can obtain a point forecast, an actual expected demand that includes any expected growth, as well as a measure of how inaccurate this forecast may be. The greater the expected variability of demand, the more excess capacity and/or inventory you need to have available.

Choosing an appropriate capacity is difficult when you don’t know for sure what demand will be. If demand occasionally spikes above process capacity, as shown in areas B and D in Figure 7-1, customers will either leave the line or cancel their order prematurely (reducing profit immediately) or not return to your company the next time they want your product. This reduces customer demand, revenue, and profit.

Illustration by Wiley, Composition Services Graphics

Figure 7-1: Relationship of demand and ­capacity.

If you’re concerned about disappointing customers, you can increase capacity to the level of peak demand and always be able to service every customer. But this may lead to further underutilization of your resources because they’re already underutilized in the times shown by areas A, C, and E in Figure 7-1.

If you carry inventory, you can build up an inventory during area A in Figure 7-1, as the demand during that period is less than capacity. You can then sell off that inventory during period B, when demand is greater than capacity. Similarly, you can build up inventory during period C to cover a shortfall in capacity in period D, and so on. This approach allows you to satisfy most, if not all, demand while maintaining a high utilization of resources, hence improving ROI. We provide more information on balancing capacity and inventory levels later in this chapter in the section Balancing Capacity and Inventory.

Timing adjustments just right

In most industries, capacity is typically added in chunks, known as step increases, because adding a single unit of capacity is impractical. If demand exceeds a company’s current capacity, then the company must increase capacity by either acquiring more equipment or hiring additional workers.

The equipment or worker has the capacity to do a fixed amount of work, which steps up the company’s capacity. For example, in an electronics firm, the smallest component placement machines (which put the integrated circuits, resistors, and transistors on the circuit board) produce several thousand parts per year. You can’t buy a machine that only produces several hundred. In services, you simply cannot hire a nurse for less than half time, which means that you’ll need to increase capacity in steps of about 120 patients per month.

Always make sure that when you add capacity, you add it to the correct parts of the process (often the bottleneck, as described in Chapter 3) to avoid allocating resources to improvement efforts that don’t meet your goals.

The step process can make planning capacity decisions even more difficult, especially when you require new facilities because predicting demand gets harder as you consider time periods farther in the future. Keep in mind that a forecast for demand this month is likely to be much more accurate than a forecast for demand a year from now. The longer it takes to build additional capacity, the less certain you can be of actual demand at that time.

You may need several months or longer to build a new manufacturing facility or retail outlet, and training new employees also takes time. Building capacity at the right time ensures that goods and services are available when customers demand them. If your timing is off, you may miss sales or find yourself sitting on excess capacity.

Figure 7-2 shows capacity being added in a step function pattern to match increasing demand. Each new piece of equipment or worker adds to the capacity in defined amounts. A restaurant, for example, hires an additional server who can serve ten customers per hour.

Illustration by Wiley, Composition Services Graphics

Figure 7-2: Adding capacity.

Demand can also decline. In this case, step issues are a problem for the same reasons they are for managing increasing demand; similar issues arise. If lower demand results in firing people, then problems with workplace morale, employee discontent, and so forth can also occur. Chapter 18 covers the product life cycle.

Balancing Capacity and Inventory

How do you manage your capacity to make sure you always have enough inventory to serve customers while keeping inventory levels as low as possible? Or, looking at it from the other direction, how much capacity should you have and exactly how much inventory should you build up during the periods when you have more capacity than demand?

When you set out to determine how much capacity and inventory you need, the first thing to do is analyze how inventory can build up over the long run, given a set capacity. Consider the process shown in Figure 7-3.

Illustration by Wiley, Composition Services Graphics

Figure 7-3: Balancing supply and demand with inventory.

Think of the supply into and the demand from an inventory as a pair of operations. In this case, let the capacity of the supply operation, representing what you can produce during any time period, be equal to S, and for maximum efficiency, we will produce at maximum capacity for the entire time period. Let the capacity of the demand operation, or customer demand during the time period, be equal to D. The supply represents the inflow, and the demand is the outflow of the stock of inventory.

Ideally you want S to equal D, but because of variations in D, you encounter periods when D is either less than or greater than S. When S is greater than D, items accumulate in inventory; when D is greater than S, items are pulled from inventory. The following equation shows the amount of inventory at any time, represented by b, given an initial inventory at time a:

In the equation, in(t) is the inflow from S, and out(t) is the outflow from D.

If the sight of a calculus equation makes you sweat, relax; you don’t need it to figure this out. Consider a simple example to illustrate how the concept applies: My favorite bakery in the North End of Boston makes tiramisu desserts that are world famous. The cakes are popular with the locals, and tourists are known to wait in the streets on a busy summer evening to purchase one. The demand for tiramisu during the first 6 months of the year is 1,800 cakes per month. Demand increases to 2,500 cakes per month the second half of the year, during the high tourist season and the holidays. The bakery has a maximum capacity to produce 2,000 cakes per month.

Figure 7-4 shows the demand and capacity over the course of a year.

The bakery has several operating alternatives for producing tiramisu:

Produce cakes only as they’re ordered and maintain no inventory, a strategy known as make-to-order. This is often referred to as chase demand strategy because the firm matches production to the expected demand for the period.

Produce cakes all year at capacity and maintain an inventory to cover increased demand during the second half of the year, an approach known as make-to-stock. This is also often referred to as a level production strategy because the firm maintains a constant output.

Increase capacity above current levels, which reduces inventory needs.

In general, carrying inventory is less expensive than carrying idle capacity, and inventory is more flexible if demand doesn’t materialize because you don’t need to build it up or you can save it for sale later. In comparison, idle capacity wastes money on excess equipment, floor space, maintenance, and possibly idle labor. But you also pay a price for inventory; inventory incurs the holding costs of tied-up capital for storage space, shrinkage, obsolescence, and quality. Flip to Chapter 8 for more on the true costs of inventory.

Illustration by Wiley, Composition Services Graphics

Figure 7-4: Tiramisu capacity and demand.

Producing to match demand

If the bakery described in Figure 7-4 chooses to produce cakes only at the rate of demand and maintain no inventory (chase demand strategy), then during the first 6 months of the year, it produces only 1,800 cakes per month. Its supply (or thruput) is less than its capacity, and its utilization (how busy resources are) is

During the second half of the year, the bakery works at a capacity of 2,000 cakes per month but loses sales of 500 cakes per month because it can’t fulfill customer demand. Over the 6 months, the bakery loses sales of 3,000 cakes. Assuming that it makes a profit on each cake, this results in a considerable loss in profit.

In this case, if the bakery wants to avoid losing sales while maintaining a zero inventory policy, it needs a capacity equal to the maximum demand of 2,500 cakes per month. The bakery can avoid some of these lost sales without adding capacity if it uses the downtime in the first half of the year to produce cakes for inventory, as shown in the next section.

Producing at capacity

If the bakery doesn’t want to send away 500 customers per month, it can produce at capacity and accumulate inventory over the first 6 months (level production strategy).

An inventory buildup diagram, or IBD, is a simple visual tool that shows the current level of inventory over time. Figure 7-5 shows the buildup of inventory over the year if the bakery described in Figure 7-4 produces at capacity, assuming that it begins the year with zero cakes in inventory.

Illustration by Wiley, Composition Services Graphics

Figure 7-5: Inventory of tiramisu cakes.

If the supply and demand is constant between time a and time b, as is the case with the bakery in this example, then the inventory at time b is equal to

During the first 6 months, the bakery produces 200 more cakes per month than demand (2,000 – 1,800), and these 200 cakes go into the inventory freezer. After 6 months, the inventory peaks at 1,200 cakes (200 × 6).

At month 7, demand for cakes increases to 2,500 per month. Because the bakery can only produce 2,000 per month, it needs to sell 500 cakes per month from the inventory to meet demand. Over the second half of the year, it needs 3,000 cakes in inventory to meet all the demand in the second half of the year.

This won’t work because the bakery only has 1,200 cakes in inventory. At some point, the bakery will deplete the inventory in the freezer and be unable to meet demand. You can calculate the time at which the bakery no longer has inventory by rearranging the earlier equation:

If you then set Ib equal to zero and solve for Tb, you know that the bakery will run out of cakes at time equals 8.4 months. From month 8.4 on, the bakery won’t be able to meet all its demand. During the last 3.6 months (12 – 8.4), the bakery won’t be able to meet the demand of 500 cakes per month, resulting in total lost sales of 1,800 cakes. This number is a bit better than the loss the bakery incurs when not carrying inventory, but it still represents a significant loss in sales.

Increasing capacity

To minimize lost sales, the bakery could increase its capacity. To prevent any lost sales without carrying inventory, the bakery needs its capacity to equal the peak demand. In this case, it needs a capacity of 2,500 cakes per month to meet demand during the second half of the year. However, this leads to a low utilization of resources during the first half of the year — only 72% (1,800 ÷ 2,500).

The bakery could choose a capacity between the original 2,000 per month and the maximum of 2,500 per month, as long as it’s willing to hold inventory during some point in the year. The bakery may decide to acquire capacity equal to its average demand of 2,150 cakes per month, operate at capacity all year, and allow inventory to accumulate.

Following this analysis, the bakery produces an extra 350 cakes each month during the first half of the year. This results in a maximum inventory level of 2,100 cakes. During the last 6 months, the bakery produces at capacity and pulls 350 cakes out of inventory each month, leaving zero inventory at the end of the year. Figure 7-6 shows the IBD for this scenario. At this capacity level, the bakery can meet all demand, but doing so requires that the bakery allow a maximum inventory level of 2,100 cakes.

Illustration by Wiley, Composition Services Graphics

Figure 7-6: Inventory of tiramisu cakes with increased capacity.

Addressing Wait Time for Services

Doesn’t it seem like you’re always waiting for something, especially when it comes to service? You wait in line to purchase a movie ticket, to check out at the grocery store, and to get cash at the automated teller machine (ATM). While this problem is endemic to most face-to-face services, it also is present in some industries, such as make-to-order PC manufacturers.

Waiting is a critical component of a customer’s perception of service quality. On the one hand, customers intensely dislike waiting. If they feel like they’re waiting too long for service, they may leave the line (or cancel their order) prematurely and may or may not return. Both actions reduce customer demand, and eventually revenue and profit take a hit as a result. But that’s not all; longer customer waiting times also increase the costs for doing business because waiting times equal more customers in a company’s building, and this requires space and stress on employees who must deal with grumpy customers.

Managers can reduce waiting times by increasing capacity, which is also expensive and reduces profit. Finding a waiting time that customers find acceptable while keeping utilization reasonably high is thus critical to efficient operations. But the calculation is not intuitive, because average waiting times can be quite long, even when capacity is significantly greater than demand.

In this section we examine the mechanics of waiting: what causes it, how you calculate expected wait times, how you reduce wait, and how you can manage negative customer perceptions when they must wait.

Getting the why of waiting

When the demand for a service exceeds the capacity of that service, waiting is inevitable. Surprisingly, however, even when process utilization is less than 100 percent, waiting can still be part of the customer experience.

Here are the primary causes of waiting:

Insufficient capacity: There’s a direct link between wait times and resource utilization.

Variability and “lumpiness” in customer arrival rates: Arrival rates vary from time period to time period and also within a given time period.

Variability in the time it takes to serve a customer: Not all customers require the same amount of time with a server. Although companies often state an average service time, some customers take longer; some take less.

Lacking capacity

In any process, if average demand is greater than the average capacity, the line grows indefinitely as resources aren’t able to keep up. Even if average demand is less than the capacity, expected flow time (the time a customer takes to get through your process, including wait time) grows with increasing resource utilization.

Figure 7-7 illustrates the relationship between utilization and wait times. The flow time remains fairly constant until about 80 percent utilization. When utilization reaches 85 percent, the flow time begins to increase exponentially (the shape of this curve comes from the Sakasegawa approximation covered later in the Estimating waiting time with queuing theory section).

Illustration by Wiley, Composition Services Graphics

Figure 7-7: Relationship between utilization rate and flow time.

Accommodating differences in arrival time and service duration

Demand fluctuations are a major cause of waiting. Figure 7-1 shows, if demand equals customers arriving per hour, capacity is greater than the average customer arrival rate (average demand). Because firms can’t perform services such as haircuts, medical appointments, and car repairs in advance during periods A, C, and E, they’re unable to create “inventories” of services to await future customer arrivals when capacity exceeds demand. So customers arriving during periods B and D experience a wait. A client arriving during periods A, C, and E may also experience a wait due to the statistical nature of arrival rates.

Customers don’t arrive in a predictable and steady pace. It varies. For example, a restaurant experiences a peak lunch demand between 11 a.m. and 2 p.m. If the average arrival rate during these three hours is 60 groups per hour, that doesn’t mean that a group arrives every minute; instead, several groups may arrive within minutes of each other and several minutes may elapse with no arrivals.

Similarly, some customers take longer to process than others. A grocery store cashier takes longer to process a customer with a full cart than a customer with only a few items. A restaurant server usually needs more time to process a group of eight than a table of two.

This variation occurs because customers arrive independently of one another. Knowing one customer’s arrival time tells you nothing about another’s. This results in a something called a Poisson arrival process.

In Poisson processes, people do not coordinate their arrival times or needs for service with each other (that is, they aren’t coordinated to arrive by appointments or reservations). Under these conditions, the time between individual arrivals is exponentially distributed.

Numerous studies of face-to-face services have shown that the time required to process each customer is also often exponentially distributed. If you don’t know the distributions of either the times between arrivals or the durations of their service, the best default assumptions are that they both have exponential distributions.

Here are the important things to know about exponential distributions:

They don’t follow a normal or bell curve distribution. Most random phenomena are normally distributed, which unconsciously or not conditions people’s intuition about random behavior. Because arrivals are exponentially rather than normally distributed, arrivals seem “clumpier” than what most people expect (despite the fact that they are indeed perfectly random). Because service times are exponentially (rather than normally) distributed, the number of horrible wait times is also much greater than most people would intuitively expect.

The mean (expected value) of the distribution equals the standard deviation. This helps you out in the next section when you’re figuring out waiting times.

Estimating waiting time with queuing theory

Wouldn’t it be helpful if you had a way to know how many people you need to schedule for a shift to operate at full capacity and utilization or how long a customer needs to wait on a given evening to get a table in your restaurant? It turns out that you can use some relatively simple equations to calculate average expected line length and wait times. Queuing theory provides these equations.

Queue, by the way, is originally the British word for a waiting line. American operations management professionals use it as well.

Before you can understand how queuing theory works, you need to familiarize yourself with the following terms and their definitions:

Queue: A line (or buffer or inventory) feeding a number of servers

Server: An operation fed by a queue

Arrival rate (λ, lambda): The mean number of arrivals per unit time, usually per hour or per day

Service rate (μ, mu): The mean number of customers that can be served at 100 percent utilization by each individual server per unit time; at the individual workstation level, the service rate equals capacity

Thruput: The number of customers actually served

Channel (M): The number of parallel operations connected to an individual queue

Utilization (u): A measure of how “busy” the system is — utilization is generally defined as the ratio of thruput to capacity

Phase: A queue and its connected servers

Line length (Lq): The average number of people in a line awaiting service

Wait time (Wq): The average time a customer waits before being served.

Figure 7-8 shows a two-phase queuing system. Each phase has two servers or channels being served by the one queue.

Illustration by Wiley, Composition Services Graphics

Figure 7-8: Example of a two-phase queuing system.

Connecting the dots little by little

A simple relationship exists between the average line length, the average customer arrival rate, and the expected waiting time. This relationship is known as Little’s law and is represented by this equation:

To illustrate the simplicity of this equation, consider the example in Figure 7-9. You arrive at a vending machine to find 8 people waiting in line ahead of you, and you estimate that each person takes 1 minute to complete his transaction, giving the vending machine a capacity to process 60 customers per hour. Because of the line, you can assume that the vending machine is 100 percent utilized (at least during the time you’re in line). In this case, thruput is equal to capacity.

Illustration by Wiley, Composition Services Graphics

Figure 7-9: Applying Little’s law.

Using Little’s law you can estimate your wait time:

You’ve probably used this relationship without realizing it many times as you stood in line and wondered how long the wait was going to be.

You can apply Little’s law in any system in which the mean waiting time, mean line length (or inventory size), and mean thruput (outflow) remain constant. Always measure the thruput as the number leaving the system, not entering it.

When using Little’s law or other queuing equations, process utilization must be less than 100 percent. Otherwise, the line would grow forever because the process can’t keep up with the arriving customers. With a utilization less than 100 percent, the average inflow equals the average outflow over time. Here is the variation of Little’s law most often used in queuing problems in this case:

Going beyond Little’s law

If you don’t know the line length or the waiting time, but you have the system’s thruput value, then you can calculate average line length and waiting time if you make a few assumptions.

Hirotaka Sakasegawa, an operations management professor at Waseda University in Japan, empirically derived a formula to analyze waiting lines. Here is a simplified version of his formula:

This equation gives a good approximation of line length if the following conditions occur:

Utilization is less than 100 percent.

The equation shows that if u equals 1, then the line length is undefined. If u is greater than 1, then the line length is negative, which is impossible.

A customer intending to enter the line does so no matter how long the line is.

Customers don’t exit the line until they’re served.

An infinite number of customers can enter the line.

The distributions of the time between arrivals and the duration of the service times are both exponential.

To illustrate this equation, imagine that 72 customers arrive randomly each hour at a fast-food restaurant. Five cash registers are open, and each register has its own line. Assuming the customers distribute themselves equally across the 5 service lines, 14.4 customers per hour arrive in each of the 5 lines. The cashier requires an average of 4 minutes to process each customer.

The first thing you need to do is calculate the utilization of a cashier. Because a cashier has the capacity to process 15 customers per hour (60/4) and only has to serve 14.4 customers per hour, each cashier’s utilization, u, is 96%. In this case, you have one line feeding each resource, giving you an M of 1.

Using these numbers in the earlier equation, find the average (mean) line length:

Now find the average wait time using Little’s law:

In most cases, this wait time is much too long. To reduce the wait time to an acceptable level, how many cashiers do you need?

Figure 7-7 shows that wait times begin to explode when the system exceeds a utilization of around 85%. You can determine what arrival rate of customers gives each cashier a utilization of 85%:

Calculate the number of cashiers you need to assure an arrival rate into each line of no more than 12.75 customers per hour by dividing the total number of customers arriving by this number: 5.65 (72/12.75) cashiers. Because you can’t have a fraction of a person at any one time, the system requires 6 cashiers.

With 6 cashiers, each resource has a utilization of 80% (each cashier can process 15 customers per hour but only 12 [72/6] arrive in each line), and the new line length is

and the average wait time is

By increasing the number of servers by just one, you can significantly reduce the line length and corresponding wait time.

However, adding more servers after you reach a utilization below 85% has diminishing returns. With the addition of a seventh cashier, cashier utilization drops to 68.6%, the average line length is approximately 1.5 customers, and the average wait time becomes 8.8 minutes.

Going single file

Reducing wait time without adding servers is possible by forming one line for all the servers instead of having a separate line for each resource. For example, at airline check-ins, you line up in a single, serpentine line with an attendant at the end directing you to an open agent.

One line and 5 servers (M = 5) produces this average line length:

Find the average wait time:

You may be wondering how we determined the utilization and arrival rates. Utilization remains unchanged, regardless of whether there are multiple lines or just one, because each resource still processes an average of 14.4 customers per hour.

The arrival rate is the number of customers arriving in a queue per unit of time. Because you have only one line, 72 customers per hour enter the line.

Whenever possible, you want to have multiple resources serving one line rather than each resource serving an individual line. By combining the lines into one, you can obtain results similar to those you got when you had 6 cashiers, each with an individual line. This approach also prevents the problem and frustration of “choosing the wrong line” at grocery checkout counters, fast-food restaurants, banks, and anywhere else there are multiple server stations to choose from.

Squishing variability to reduce waiting

There’s another way to reduce waiting time. Waiting comes from the variability in the times between arrivals and the durations of the service times for customers. If you can reduce the variability in the arrival rates (through appointments or reservations) or service time duration (through standardizing the process), you can reduce waiting time still further.

Squishing variability in either situation means you’ll no longer have exponential distributions. But you can modify the Sakesagawa approximation to account for this as follows:

The coefficient of variation of the time between arrivals (CVTBA) is the ratio of the standard deviation of the time between arrivals to its mean. In other words, the CVTBA = Standard deviation (TBA)/Mean(TBA). The CV of service time duration (CVST) is, similarly, the ratio of the standard deviation of service times to their mean: CVST = Standard deviation (ST)/Mean(ST). Generally speaking, the larger a CV is for a random variable, the more spread out or random is its distribution.

You can also use this longer Sakesagawa approximation if you have some historical data for the two CVs. Note that exponential distributions always have a CV of 1.0, which is why the shorter form for Lq used in the prior two sections is really just a special case of this longer formula.

To see how squishing variability works, let’s build on the case of the fast food restaurant in the earlier Going single file section, which has one line feeding 5 servers. First we introduce a reservation system, which we find out drops the CVTBA from 1.0 to 0.4. We also work to standardize the process, so that the CVST goes from 1.0 to 0.5. The resulting line length becomes

This is a reduction of over three-quarters in the line length. This results in a similar reduction in the wait time thanks to Little’s law:

Looking at these results, you can see that using reservations (or appointments for services, as doctors and dentists do) and standardizing processes to squish variability are powerful tools to reduce wait times.

Waiting in more complicated processes

Many times you have to deal with entire processes having many stages, all of which have waiting lines rather than just the one line. How do you calculate the waiting times in these situations? It’s easier than it looks.

So long as all the arrival rates are Poisson and the service times of all the operations are exponentially distributed in a complex process, two facts let you leverage the Sakesagawa approximation for line lengths described in “Going beyond Little’s law”:

The output rate of an operation is equal to the arrival rate if utilization is less than 100 percent, and the output is also a Poisson process.

The total arrival rate into a queue is the sum of the arrival rates feeding into it.

Figure 7-10 illustrates the process at a popular cafeteria on a university campus. A student enters one of three lines, depending on what he wants for lunch. After he receives his food, he proceeds to one checkout line, which is served by two cashiers.

If the student is hungry for pizza and wants to know how long he’ll have to wait for it, he can use these equations to calculate the average line length and wait time for each of the server stations:

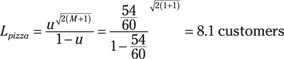
To calculate the number of customers waiting for a resource and the average time they’ll spend waiting, you need to know how many customers are exiting the three server stations and entering the checkout line.

The exit rate from each of the server stations is equal to the arrival rate because all utilizations are less than 100 percent. The arrival rate into the checkout line is the sum of the 3 exit rates. So, in this case, 115 customers per hour enter the line.

Illustration by Wiley, Composition Services Graphics

Figure 7-10: Merging lines.

Because the checkout line has two cashiers, you can find the average line length and wait time for each resource:

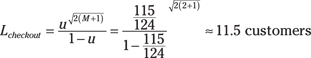
The total time that a pizza customer spends in the process is equal to the time he waits plus the time he’s being processed. This time is often referred to as the flow time (see Chapter 2). For the average pizza customer, the pizza server takes 1 minute (1/60 of an hour) to prepare the order, and the cashier takes 0.97 minutes (1/62 of an hour) to collect payment. So the total flow time is 16.97 (9 + 1 + 6 + .97) minutes for the customer to get his lunch.

Altering customer perceptions

From a customer’s perspective, two theories are in play: how long the customer waits in line and how long the customer thinks he’s waiting in line.

If you must make a customer wait, you can make the time more comfortable and seem shorter than it really is by managing the customer’s perception of the waiting time. Here are some things to know about managing customer perceptions so the wait doesn’t negatively affect satisfaction:

Customers don’t mind waiting as much if they’re comfortable. This is perhaps the most important way to influence customer satisfaction. Make sure that you have plenty of space, comfy chairs, and a pleasant atmosphere in your waiting room. Offering amenities such as refreshments, current reading material, and wireless Internet can go a long way toward softening the sting of waiting.

Preprocess wait time feels longer than in-process wait time. You want to get your customers into the process as quickly as possible. This may involve something as simple as greeting them the moment they walk in the door. After they enter, they’re less likely to leave before being served.

Unoccupied time feels longer than occupied time. You may want to break up the processing time into smaller steps with a wait between each step rather than having a longer wait time upfront. The doctor’s office is great at doing this. When you arrive at an appointment, a receptionist greets you and then you wait to be called, usually by a nurse who shows you to a room and takes your vital statistics. You then wait again in the exam room for the doctor. On average, you wait the same amount of time as if you had waited all at once at the beginning, but because the wait is interrupted, people often perceive it as being less.

Uncertain waits are perceived to be worse than certain waits. By telling customers know how long the wait will be, you remove the anxiety associated with waiting. The customers can then relax, knowing when they’ll be served.

Unexplained waits are worse than explained waits. If your customers are going to have to wait longer than expected, let them know. For example, if the doctor is handling an emergency patient, inform the others who are waiting. Customers are more tolerant of these delays. However, if the wait is longer because the doctor took an extended lunch, you probably should avoid sharing this information.

Unfair waits are worse than fair waits. Nothing is worse than feeling that other customers are cutting in line or getting preferential treatment. Having a well-defined process flow can minimize this effect.

These same principles can apply to back orders or customers waiting for build-to-order. For example, providing a website link so the customer can check the order status and a tracking number so the customer can check the shipping progress of the item can make the wait for an ordered item seem to go by faster.