Chapter 12
Managing Quality
In This Chapter
![]() Understanding how the customer views quality
Understanding how the customer views quality
![]() Exploring the costs and payoffs of quality
Exploring the costs and payoffs of quality
![]() Managing quality efforts
Managing quality efforts
![]() Building quality into the product design process
Building quality into the product design process
![]() Using various tools to measure quality
Using various tools to measure quality
Quality is an aspect of a product that leaps to the forefront of a customer’s attention when something doesn’t perform as expected. Yet producing a quality product or providing a quality service must center on well-considered operations; it doesn’t happen by accident. As an operations manager, you must ensure that quality drives every process and decision. This is sometimes a thankless effort because you’ll likely only hear about quality issues from dissatisfied customers.
In this chapter, we take an in-depth look at quality — how to define it, how to measure it, and how to determine the costs associated with it.
Deciding What Matters
When assessing quality, the first question you need to ask is, “What is a quality product?” Only your customer can answer this question because quality is what the customer says it is. A quality product means different things to different people, and expectations differ from product to product. When asking potential customers to define a quality car, for example, you get an array of answers, ranging from “A quality car starts each and every time, gets good gas mileage, and has a high safety record” to “A quality car goes from 0 to 60 in 4.5 seconds and has a sleek design.”
Making matters even more challenging is that customers, in addition to having different expectations of quality, perceive and define each of those dimensions differently. Turning those perceptions into metrics that an operations manager can act on is one of the trickiest parts of managing quality. The wrong metrics can lead to a lot of wasted effort on improving aspects of a product that the customer doesn’t value. For example, if a car company uses the wrong metric (measures the wrong aspect) to assess its pickup truck’s acceleration, then their attempts to improve this feature will be misdirected and wasted. By finding a metric that matches customer expectations, they could begin to make headway in improving the quality of this type of vehicle.
![]() Performance: The primary operating characteristics as perceived by the customer. Common performance metrics for an automobile are miles per gallon (MPG) and time to accelerate from 0 to 60 mph. Performance characteristics can often conflict because different customers value different factors.
Performance: The primary operating characteristics as perceived by the customer. Common performance metrics for an automobile are miles per gallon (MPG) and time to accelerate from 0 to 60 mph. Performance characteristics can often conflict because different customers value different factors.
![]() Features: The secondary operating characteristics or the “bells and whistles.” These are the features that surprise the customer. Features often evolve and become primary operating characteristics — for example, anti-lock brakes, which were once considered features on a car, are now standard and considered part of performance quality.
Features: The secondary operating characteristics or the “bells and whistles.” These are the features that surprise the customer. Features often evolve and become primary operating characteristics — for example, anti-lock brakes, which were once considered features on a car, are now standard and considered part of performance quality.
![]() Reliability: The consistency of the product’s performance. This dimension indicates how often the product malfunctions and doesn’t deliver on performance expectations. For an automobile, reliability is typically determined by how often the car must go back to the dealer to fix a problem. But customer perception plays a role here as well. For example, if a car company makes its power locks as quiet as possible and customers don’t like this, they may consider it a defect.
Reliability: The consistency of the product’s performance. This dimension indicates how often the product malfunctions and doesn’t deliver on performance expectations. For an automobile, reliability is typically determined by how often the car must go back to the dealer to fix a problem. But customer perception plays a role here as well. For example, if a car company makes its power locks as quiet as possible and customers don’t like this, they may consider it a defect.
![]() Durability: How long the product provides acceptable service. In automotive terms, “Do I trade in the vehicle when the warranty expires or hold onto it because it will probably outlast me?”
Durability: How long the product provides acceptable service. In automotive terms, “Do I trade in the vehicle when the warranty expires or hold onto it because it will probably outlast me?”
![]() Aesthetics: How the product looks, feels, and sounds. Some types of products, including cars and computers, often sell better purely based on looks.
Aesthetics: How the product looks, feels, and sounds. Some types of products, including cars and computers, often sell better purely based on looks.
![]() Safety: The risk of harm or injury from using the product. Safety relates to the risk of using the product correctly as well as the risks associated with using it in ways for which it wasn’t designed. How the auto performs in government crash tests is an important consideration to many customers.
Safety: The risk of harm or injury from using the product. Safety relates to the risk of using the product correctly as well as the risks associated with using it in ways for which it wasn’t designed. How the auto performs in government crash tests is an important consideration to many customers.
![]() Conformance: How well a product or service meets its design standards during actual use by the customer. For cars, a good example of a conformance requirement is advertised MPG versus MPG actually experienced by the customer. Few (if any) drivers actually get the posted MPG because the specification was obtained under ideal driving conditions with a professional driver. In other types of manufacturing, conformance can be tested in the factory. The conformance metric can be crucially important because the firm often advertises the product based on these metrics, and if the product doesn’t perform, the customer is disappointed.
Conformance: How well a product or service meets its design standards during actual use by the customer. For cars, a good example of a conformance requirement is advertised MPG versus MPG actually experienced by the customer. Few (if any) drivers actually get the posted MPG because the specification was obtained under ideal driving conditions with a professional driver. In other types of manufacturing, conformance can be tested in the factory. The conformance metric can be crucially important because the firm often advertises the product based on these metrics, and if the product doesn’t perform, the customer is disappointed.
![]() Serviceability: How well the product is serviced after the sale. This attribute relates to the speed, competence, and courtesy of customer service as well as to how the product was designed to accommodate service when a malfunction occurs.
Serviceability: How well the product is serviced after the sale. This attribute relates to the speed, competence, and courtesy of customer service as well as to how the product was designed to accommodate service when a malfunction occurs.
![]() Perceived quality: How the public perceives the quality of the product or service, which affects a company’s reputation in the marketplace. Brand loyalty is a potential outcome of perceived quality; many pickup owners strongly prefer either a Chevy or a Ford, and most are repeat buyers. An important point about perceived quality is that studies show a brand can lose it much more quickly than acquire it.
Perceived quality: How the public perceives the quality of the product or service, which affects a company’s reputation in the marketplace. Brand loyalty is a potential outcome of perceived quality; many pickup owners strongly prefer either a Chevy or a Ford, and most are repeat buyers. An important point about perceived quality is that studies show a brand can lose it much more quickly than acquire it.
These attributes of quality provide a common language for assessing a product. You can measure and compare every product along these lines. And the key to developing quality products is knowing what customers expect and identifying actionable metrics for improvement based on these expectations. Reach out to the company’s marketing department to gather reliable information on these data points.
Recognizing the Value of Quality
You may have heard the saying “Quality is free.” Implementing an effective quality system is anything but free, but the alternative usually proves to be much more expensive. This section explores the true costs and payoffs of quality.
Producing a quality product or service requires the whole organization to be onboard and involved. Quality begins in product design, requires attention in production, and must be at the forefront of customer service. A sincere focus on quality requires time, energy, and commitment; without it, a business risks lost sales and revenue, potential product liability claims if a product fails, and lowered productivity.
The primary burdens of poor quality are failure costs, detection costs, and prevention costs, which we cover in this section.
Assessing the cost of failure
Failure costs are those costs associated with producing a defective product. Two types of failures exist: those that are discovered internally and those that are detected externally.
Internal failures
Internal failures are defects discovered during the production process. When a company discovers an internal failure, it needs to discard or repair the defective part. The costs associated with internal failures are the wasted resources (labor and material) used to produce the product if it’s discarded, or the additional costs to correct the defect if it’s repaired. To see how reworking defective products affects process performance, visit Chapter 4. Internal failures also occur in service operations. A good example would be an accountant who discovers an error in a tax return before it’s forwarded to the customer and eventually the IRS.
External failures
External failures are defects discovered after delivery to the customer — either identified by the manufacturer after the product ships or discovered by the customer during normal use.
Numerous types of costs are associated with external failures, and they go well beyond a company losing money because defects are visible to the customer. In other words, the manufacturer must not only repair and replace the product but also deal with the loss of reputation, customer goodwill, and eventually market share. The actual impact of external failures varies depending on the type of customer that discovers the defect. If the customer is the end consumer, then repairing or replacing the product can quickly provide an opportunity for the company to improve or retain good quality perceptions. When the customer is a business, however, replacing or repairing the product(s) is much less likely to undo the business disruption caused by the failure.
This also applies to services; it may be very difficult to regain the trust of a client if a faulty tax return is sent to the IRS and the customer is called in for an audit as a result.
Detecting defects
Expenses associated with detecting poor quality before, during, or after production are known as detection (or appraisal) costs. Inspection and testing are the primary ways a company can find product defects.
Ideally, you want to design quality into the process for creating a product. Sometimes, in addition, inspection and testing are necessary to ensure that the process is operating as designed. To establish an inspection process, you need to decide how many products to inspect and when and where in the process to conduct the inspection.
How many products to inspect is a trade-off between the cost of inspection (which can be high if the test destroys the tested unit) and the cost of external failures if customers purchase the defective products. Most firms test a small percentage of total product output. Some statistical implications are associated with the sample size; for details, see the Measuring Quality section later in this chapter.
You have three options when choosing when to inspect a product:
![]() Incoming inspection of raw materials from suppliers: Monitoring incoming materials prevents a company from wasting resources on material that’s already defective. Proper management of the supply chain (see Chapter 10) should minimize these inspections.
Incoming inspection of raw materials from suppliers: Monitoring incoming materials prevents a company from wasting resources on material that’s already defective. Proper management of the supply chain (see Chapter 10) should minimize these inspections.
![]() Inspection during the production process: Monitoring quality throughout the process is possible with a convenient and easy-to-use statistical technique we describe in the later section Measuring Quality.
Inspection during the production process: Monitoring quality throughout the process is possible with a convenient and easy-to-use statistical technique we describe in the later section Measuring Quality.
 Where in the production process you conduct inspections is important to minimize waste. You generally want to inspect before the bottleneck operation (bottlenecks are covered in Chapter 3) to avoid putting any unnecessary burden on the resource that’s already limiting capacity. Other good points of inspection include before an expensive operation (such as gold-plating) and before an irreversible operation (such as heat treating or cutting).
Where in the production process you conduct inspections is important to minimize waste. You generally want to inspect before the bottleneck operation (bottlenecks are covered in Chapter 3) to avoid putting any unnecessary burden on the resource that’s already limiting capacity. Other good points of inspection include before an expensive operation (such as gold-plating) and before an irreversible operation (such as heat treating or cutting).
![]() Inspection of the finished product: Monitoring quality before products ship out to customers can prevent defects reaching customers. This is usually the most expensive inspection point because the product is complete and has thus already incurred all manufacturing costs; but it may prevent external failures, which can be devastating.
Inspection of the finished product: Monitoring quality before products ship out to customers can prevent defects reaching customers. This is usually the most expensive inspection point because the product is complete and has thus already incurred all manufacturing costs; but it may prevent external failures, which can be devastating.
Getting the perks of high quality
Producing and delivering high quality products and services has beneficial external and internal effects.
Internal effects
The most important internal effect of high quality is the increased ability to further improve quality. How is this so? If you have a lot of quality problems, they tend to mask one another. It’s much like a detective solving a murder case with many suspects. You can’t focus much time on any single suspect. In addition, because all suspects are being scrutinized, they’re probably unwilling to come forward with information that may help eliminate other suspects.
External effects
Externally, high quality results in a perception of reliability and value with customers over time. Customers are known to pay a premium for products — ranging from hotel rooms to vehicles — that they know they can rely on. Moreover, high quality tends to have a halo effect. In other words, if several of your products are known to be of high quality, customers will automatically assume that your other products are as well. This helps to increase a company’s market share across the board.
Preventing defects in the first place
Make every effort to prevent defects from occurring in the first place. Doing so requires that quality is designed into the product and the process that makes it. Most firms have some type of quality program in place. These programs go by many different names, including Total Quality Management (TQM) and Six Sigma. We explore the fundamentals of TQM and related concepts in the next section, and Chapter 13 describes the revolution known as Six Sigma.
Addressing Quality
The best way to manage quality is not to make defects in the first place. To do this, companies are finding that they must shift their entire focus away from who’s responsible for defects to how the process is creating defects.
Quality guru W. Edwards Deming once stated, “Workers are responsible for 15 percent of the problems; the system, for the other 85 percent. The system is the responsibility of management.” When Deming said system, he meant process as it’s typically called today. In other words, workers can only perform as well as the process allows them. Table 12-1 shows the difference in approach from the traditional to the process focus.
Table 12-1 Process Approach to Quality
|
Traditional Focus |
Process Focus |
|
Who? |
How? |
|
Doing my job |
Getting things done |
|
Knowing my job |
Knowing the process |
|
Motivate |
Removing barriers |
|
Measure the workers |
Measure the process |
The Toyota process improvement methodology (also known as kaizen) and its offspring, including Total Quality Management (TQM) and Six Sigma (see Chapter 13), are all movements toward improving quality with a process approach. They provide a new way to look at quality and focus on changing the culture of an organization to achieve continuous improvement. Without the cultural changes these concepts propose, companies can’t realize maximum quality improvements.
Kaizen, TQM, and Six Sigma encompass three fundamental principles: a focus on customer satisfaction, participation by everyone across the organization, and an endless quest for continuous improvement and innovation. In this section, we look at each of these principles.
Considering the customer
As we mention earlier in the chapter, quality is what the customer says it is. Worse yet, customers’ expectations are always changing (and usually ratcheting upward!). So to define quality, you must know what’s important to your customers and keep updating that knowledge over time. Automobile customers, for example, vary greatly on the attributes they want a car to have. It’s the rare vehicle that can deliver to all customers on all dimensions, especially when price is an important factor in the purchasing decision. Delivering a product the target customer wants requires a concerted effort among marketing, product design, and operations/production.
Getting all hands on deck
Participation by everyone across the organization is critical to the success of any quality improvement project. Line workers are often the first to recognize process problems that contribute to poor quality. They perform the operations day in and day out and are the best source for identifying and implementing improvements. Maximizing the potential of line workers requires that they’re well trained and educated on the entire process, not just their individual jobs.
Upper-management support is also critical. Implementing quality improvement projects often requires significant time and resources. Management must be willing to suffer potential short-term productivity losses for the sake of long-term improvement. For example, in many innovative manufacturing facilities, line workers have the power to pull a cord and stop the assembly line if they observe poor quality. This could never occur if management is more concerned with the volume of daily production than the end quality of the products.
Others need to participate as well. Stopping the line frequently requires that employees, including maintenance and supervisors, can be dispatched quickly to the problem area and that they have the training and ability to resolve quality issues quickly so that production can resume. See Chapter 11 for details on the attributes of companies that have successfully implemented this policy.
Sticking to the improvement effort
Kaizen, TQM, and Six Sigma all focus on continuous improvement, which is the crux of any successful quality-focused program for two reasons:
![]() Quality is much like learning to play a musical instrument. If you give up practicing every day, then you won’t improve anymore, and you’ll actually get worse.
Quality is much like learning to play a musical instrument. If you give up practicing every day, then you won’t improve anymore, and you’ll actually get worse.
![]() Customer expectations tend to increase over time, so quality needs to improve to keep up.
Customer expectations tend to increase over time, so quality needs to improve to keep up.
But how do you actually accomplish continuous improvement? Figure 12-1 illustrates the cycle that underlies all continuous improvement efforts.

Illustration by Wiley, Composition Services Graphics
Figure 12-1: The plan-do-study-act cycle.
This figure, known as the plan-do-study-act cycle, is also called the Deming wheel or the PDSA cycle. It represents the circular nature of continuous improvement. As you solve one problem, you continue on to the next problem. The process has four steps:
1. Plan: You must plan for improvement, and the first step is to identify the problem that you need to solve or the process that you need to improve.
After you identify the problem/process, you need to document it, collect data, and develop a plan for improvement. (For more information on how to identify and select problems, see Chapter 13.)
2. Do: You then implement and observe the plan.
As in Step 1, you should collect data for evaluation.
3. Study: You need to evaluate the data you collect during Step 2 (the do phase) against the original data you collected from the process to assess how well the plan improved the problem/process.
4. Act: If the evaluation shows improved results, then you should keep the plan in place (and implement it more widely, if appropriate).
Then it’s time to identify a new problem and repeat the cycle. On the other hand, if the results aren’t satisfactory, you need to revise the plan and repeat the cycle. Either way, you repeat the cycle!
This PDSA cycle is also the foundation behind the DMAIC method of the Six Sigma process improvement methodology, which we describe in Chapter 13.
Designing for Quality
Quality begins with a product’s design, which determines how well the product will meet customers’ needs and, to a large extent, drives the cost of production. Therefore, it’s critical that marketing, product design, and manufacturing work together.
Quality function deployment (QFD) is a structured approach for integrating customers’ requirements into a product; it’s also the process used to create the product. The house of quality (HOQ) is a tool to accomplish this integration.
In this section, we introduce the concepts behind the HOQ and show you how to develop a cascade of such houses to take you from your customers’ requirements to a process capable of producing a product that meets those requirements.
Starting with the end in mind
Just as two of the three little pigs learned, if you don’t build a quality house — in the case of these famous pigs, a quality house is one that can survive a wolf’s huffing and puffing! — then you may find yourself without shelter. The same principle of building in quality applies when designing any other product. The HOQ ensures that quality is designed into a product from the start. Figure 12-2 illustrates an HOQ.
When building your house, you want to start with the customer requirements, which are usually called the voice of the customer (VOC). This is what the customer needs and wants from your product. Generally, VOC is expressed in qualitative terms such as, “I want a house that will keep a wolf out.” Later, you put quantitative measures on the requirement: The house must withstand a 100-mph wind gust.

Illustration by Wiley, Composition Services Graphics
Figure 12-2: House of quality.
Developing a VOC that captures exactly what your customer expects requires market research and an intimate knowledge of your potential customers. Be aware that some of the customer requirements may conflict with each other. For example, requirements to keep the wolf at bay and to take advantage of the mountain views from the living room may conflict. Because of the potential conflicts, ranking requirements based on their importance to the customer is often necessary.
After capturing the VOC, you need to establish the product’s technical requirements — how you’re going to deliver the customers’ wants. These are listed in the top “room” of the house and are general characteristics of the design. For the pigs’ house, technical requirements may be wall thickness and number of windows.
The specifications or target values associated with the technical requirements are detailed in the lowest level of the house, as shown in Figure 12-2. Here, you list quantitative specifications, such as 6 inches for wall thickness and at least 5 windows.
The main room of the house is the relationship matrix; it shows the correlation between each VOC and technical requirements. Typically, four possible conditions exist: strong, medium, small, and negligible. For example, a strong relationship exists between the take-advantage-of-the-mountain-views VOC and the number-of-windows technical requirement. The more windows, the more open the view.
The triangular attic at the top of the house contains the correlation matrix and shows the relationship among the product’s technical requirements. Each requirement can have a negative, strong negative, positive, strong positive, or no relationship with the other requirements. For example, wall thickness has a strong negative relationship with the number of windows because windows are relatively thin, while an insulation requirement has a positive relationship with wall thickness.
The correlation matrix helps identify key requirement conflicts. Product designers must find ways to overcome the conflicts or decide what trade-offs they need to make in the design. In the case of the pigs’ house, the designer may be able to add shutters to the windows that the pigs can open in the absence of the wolf to provide the view, and they can close them when the wolf threatens. Shutters, however, add to the cost of building the house, which may dissatisfy the customer, especially if cost is one of the important customer requirements.
The last room of the house is the competitive assessment. This room allows you to rank yourself against your prime competitors and highlights weakness in your product. Typically, you want to access your existing product (if one exists) and several other products in the marketplace. You usually gather the measures in this house from customer surveys. The first measure is the importance rating (often displayed in room 1). This metric has the customers rank each requirement on how important the requirement is to them. The second measure is a satisfaction rating that indicates how satisfied the customer is with the existing products along each requirement. Scales for the measures vary. A typical scale may be 1 to 5 or 1 to 3, with the higher number indicating greater importance or greater satisfaction.
Cascading to production
Most often, one house isn’t sufficient to translate the VOC down to actual production. You can use QFD to build cascading houses where the technical requirements of one house are transformed into the customer requirements of the next. Figure 12-3 shows cascading houses that start with the customer requirements of the first house and end with the development of a house for production.

Illustration by Wiley, Composition Services Graphics
Figure 12-3: Cascading houses of quality.
Building starts with developing the initial HOQ as described in the preceding section. You repeat the process by using the first set of technical requirements (product requirements) as the new VOC and then developing a house for the part (or component) requirements. This house assigns the product technical requirements to the component responsible for providing them.
This continues to the process planning house, where the hows from the parts house become the whats for the new one, and a new set of requirements is developed. The final house, using the process requirements as the VOC, provides the manufacturing requirements that are used to produce the product. The end result is a structured way to connect the actual wants of the customer through product and process design to the manufacturing floor.
Measuring Quality
Much of process improvement is about reducing defects. A defect results when some aspect of the product or service falls outside of the customer specifications. The causes of defects include a production process that is out of control — or unstable — and poor design objectives that did not incorporate customer requirements.
This section describes how to measure a process to determine whether it’s out of control and to see how prone a process is to producing a defect. We examine the concept of variation and its effect on product quality. We also introduce a common tool for measuring process variation (you can find more tools in Chapter 13) and present methods for controlling the process.
Understanding variation
No two products are exactly alike; many sources of variation exist in the processes that create a given product. Variation is the change or difference in condition, amount, or level of some aspect of a product or process. From a process and quality perspective, two types of variation exist: common cause variation and special cause variation.
Common cause variation is the random variation that occurs naturally in a system. Countless and unavoidable factors create variation. For example, a machine used to drill a hole in a piece of material won’t always produce a hole with the exact same diameter. Some natural variation is inevitable. This variation is generally tolerable within a certain range.
The output from any process can be characterized by an arithmetic mean and a standard deviation. The mean of the process is simply the sum of all observations divided by the total number of observations. The standard deviation is a measure of how the observations differ around the mean, which is the square root of the variance of the distribution.
Special cause variation, on the other hand, is variation that can’t be explained by common cause variation. It can be assigned to a specific source, though, and then eliminated. For example, in the drill machine example, if a drill bit breaks, the machine will produce holes with diameters that can’t be explained by common cause variation. After you identify the cause of this variation, you can fix it — in this case by replacing the drill bit. Variation should return to the common cause range after the special cause issue is addressed.
Process variation is a core aspect of most quality problems. Moving the mean of a process is much easier than reducing the variation of the process. For example, look at the targets of two hunters presented in Figure 12-4. Hunter 1 shoots consistently to the right of the bull’s eye. Although he’s off of the bull’s eye, his shots have very little variation in location. On the other hand, the shots of Hunter 2, though centered around the bull’s eye, are spread considerably (high variability in location).

Illustration by Wiley, Composition Services Graphics
Figure 12-4: Target practice.
Hunter 1 simply needs to move the mean of his shot to correct the variation; he can probably accomplish this by adjusting his scope. This would be an example of a special cause variation. Hunter 2, on the other hand, appears to have a twitchy trigger finger or some other problem that causes him to jerk the gun barrel when he shoots. He’ll have a harder time identifying and correcting the cause of his missed shots.
Measuring “goodness” of a process
Assuming that the process is operating within common cause variation means that no special causes are active. Thus, the process is stable. However, this doesn’t mean that the process is “good.” For example, a process may consistently make Oreo cookies with a certain amount of filling, but this amount of filling may not satisfy the customer.
The typical way to measure a process is to determine its capability — or the process’s ability to satisfy the customer. You can determine process capability in a number of different ways, but the most common way is to use standard deviations (often called sigmas by operations management personnel) from the mean.
Consider, for example, how long it takes to fly from Austin, Texas, to New Orleans, Louisiana. If you measure the length of a couple of hundred flights, using statistical equations you find that the mean of this process (μ or mu) is 90 minutes and that the standard deviation (σ or sigma) is 5.75 minutes. If you assume that the distribution of times is normal, then you’d expect flight times to exhibit the pattern shown in Figure 12-5.
What you don’t know is whether this process produces acceptable results in terms of customer specifications. To find out, you need to place some specifications on the process.
Generally, airlines believe that being 15 minutes late doesn’t upset customers, but anything more results in dissatisfaction. So if the flight exceeds 105 minutes (90 + 15), then it’s considered a defect. Similarly, arriving more than 15 minutes early is problematic because customers may need to wait for their ride home or other reasons, so arriving in less than 75 minutes (90 – 75) is also defective.

Illustration by Wiley, Composition Services Graphics
Figure 12-5: Normal distribution with 3 sigma.
These two parameters (75 and 105 minutes) are referred to as the lower and upper specification limits (LSL and USL) for the process or the range of “good” flight times as specified by the customer. Whenever a process results in a measurement outside the two specification limits, a defect exists. The LSL and USL for flight times are also shown in Figure 12-5.
Calculating the process capability ratio (Cp)
Many kinds of businesses, including those in the automotive industry, use metrics that are different from the sigma level to measure process capability. The first one is the capability ratio (Cp). Calculate the process capability ratio using the following equation:
![]()
If the ratio is less than 1, the process creates products that are outside the specifications assuming a normal distribution, which means it will produce some defects even though no special cause variation exists and the process is in control, meaning that the process is stable over time and has no active special causes. The smaller the Cp, the greater the number of defects.
Not many people use this measure because, unlike the sigma capability described in the previous section, it doesn’t account for whether the mean of the parameter is off-center (the mean value the process is creating is not the mean value of what the customer expects). However, a modification of this calculation, called the ![]() , accounts for the parameter being off center and is more popular.
, accounts for the parameter being off center and is more popular.
Calculating the process capability index ![]()
The process capability index accounts for the fact that a process doesn’t necessarily operate at the center of its specification limits. This can be a problem because a process with a very small standard deviation can produce parts outside customer specifications because the mean of the process is off-target.
As an extreme case, if the mean lies right on top of the LSL, then half the parts would be outside the specification limit. So a metric that accounts for the potential of defects resulting from the mean lying near the USL or the LSL is necessary. Most firms address this problem by calculating the process capability index using the following equation:
![]()
The ![]() is simply the minimum value of the difference between the mean μ
is simply the minimum value of the difference between the mean μ
and the LSL divided by 3σ or the difference between the USL and the mean divided by 3σ.
The process capability index is simply the process capability measured in sigmas, as described earlier, divided by 3. For example, a 4-sigma quality process has a ![]() of 1.33 (4/3).
of 1.33 (4/3).
After determining how a process is expected to perform, how do you evaluate further output from the process to determine whether it’s performing as it should? Find out in the next section!
Controlling processes
Statistical process control (SPC) is a set of statistical techniques that determine whether processes are behaving as expected. If a process is behaving as expected, it is in control. Being in control is the same as having no special cause variation present (described earlier in the section Understanding variation). In other words, a process that’s in control is behaving the same today as it was yesterday; it’s stable. On the other hand, if the process is not behaving as expected, then it’s out of control.
A process’s status as in control doesn’t mean that it’s necessarily producing good parts, merely that it’s behaving as it has in the past without any special cause variation. A process can be in control and still produce a large number of defective parts. The reason it matters whether a process is in control is because this status determines that it’s stable. If the process isn’t stable, a number of problems can exist.
The most common SPC tool is a control chart, which is a plot of samples taken from the process over time. A control chart provides a simple visual to help operation managers monitor a process to see whether it’s performing as expected.
The idea is simple. After you establish the initial control limits, you can take a sample from the process at the specified time period — every day or every hour, shift, or week — and then plot results on the chart. You look for measurements that lie outside two calculated control limits. If no measurements lie outside these control limits, then theoretically the process is in control. If a measurement is outside the limit, then the process has changed and is unstable. In other words, if a value falls outside the control limits, then you know that a special cause of variation has occurred or is occurring in your process.
Monitoring the process using an x-bar chart
Control charts for variables monitor the mean (![]() -chart), also called an x-bar chart, and the range (R-chart) of the process.
-chart), also called an x-bar chart, and the range (R-chart) of the process.
With a number of these sample means (![]() ) in hand, you can calculate the mean of the sample means (
) in hand, you can calculate the mean of the sample means (![]() ) and the standard deviation of the sample means (
) and the standard deviation of the sample means (![]() ). Then calculate the UCL and LCL as follows:
). Then calculate the UCL and LCL as follows:
![]()
Figure 12-6 shows a typical x-bar control chart. If a sample mean falls outside the control limits, then you know that the process has changed in some manner. This change can be attributed to a special cause and hopefully identified and eliminated.

Illustration by Wiley, Composition Services Graphics
Figure 12-6: Example of a mean control chart.
In general, if the specification limits are within the control limits, then the process has a high probability of producing defective products. If, however, specification limits are outside the control limits, then the process has a high probability of producing defect-free products. Figure 12-7 illustrates how the CL and the SL influence quality levels.

Illustration by Wiley, Composition Services Graphics
Figure 12-7: Relationship between control limits and specification limits.
Often, the standard deviation of a process is not known. If this is the case, you can use the average of the sample ranges (![]() ) to calculate the UCL and LCL. Here are the formulas for these calculations:
) to calculate the UCL and LCL. Here are the formulas for these calculations:
![]()
Table 12-2 shows the value of A2 for the different number of observations in the subgroup. As you notice from the table, the value of A2 declines as the number of observations increases, which produces a smaller control range.
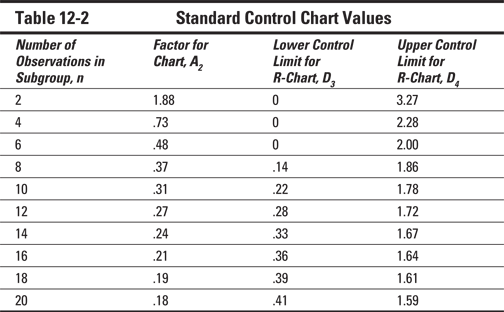
Constructing a range chart
The construction of a range chart is similar to the construct of a mean chart. Find control limits for a range chart by using the average sample range and the following equations:
![]()
The values of D3 and D4 are shown in Table 12-2.
Monitoring attributes
Attributes are counted. For example, you can count the number of products that have a defect in a sample or the number of scratches on the surface of a product. Two charts used to monitor attribute quality are the p-chart and the c-chart.
Constructing p-charts
A p-chart monitors the proportion of defective products. In a p-chart the product is inspected and is categorized as either good or bad. The underlying distribution of a p-chart is binomial (the discrete probability distribution of the number of successes given experiments with two outcomes, such as good/bad). However, the normal distribution provides a good approximation if the sample sizes are large enough.
The central line of a p-chart is the average fraction defective. You can calculate the standard deviation from the following equation when p is known:
![]()
Calculate the control limits using the above standard deviation for a p-chart:
![]()
If p is unknown, you can estimate it from samples. The estimate, ![]() , replaces p in the control limit formulas.
, replaces p in the control limit formulas.
To use a p-chart, inspect a sample of products (n) and count the number of defective items. Calculate the proportion of defective items against total output and plot this ratio on the chart. If the ratio goes above the UCL, then something undesirable has happened to the process.
Just keep in mind that getting a ratio below the LCL is actually desirable. You want the proportion of defects to be low, so a number below the LCL indicates that the process may have improved. If it has improved, that’s great, but you’ll need to reestablish your p-bar and set up new control limits.
Constructing c-charts
In many cases more than one defect exists on a product. The c-chart monitors the number of defects on any one product. The underlying sampling distribution is known as Poisson.
In a c-chart, the center line is the average number of defects per product ![]() , and the standard deviation is
, and the standard deviation is ![]() . You can calculate the control limits with this equation:
. You can calculate the control limits with this equation:
![]()
Using control charts
Mean and range charts monitor different aspects of a process. Mean charts quickly reveal when shifts appear in the mean; range charts show a shift in the variability of the process.
When using control charts, you can experience two types of errors:
![]() Type I errors (or false positives) occur when you conclude a process is not in control when it actually is. Type I errors occur because a normal distribution always includes some occurrences in the tail (take a peek at Figure 12-5 to see what we’re saying here).
Type I errors (or false positives) occur when you conclude a process is not in control when it actually is. Type I errors occur because a normal distribution always includes some occurrences in the tail (take a peek at Figure 12-5 to see what we’re saying here).
![]() Type II errors (or false negatives) occur when you conclude a process is in control when it’s actually out of control. That is, even if all values on your control charts are within the control limits, it’s still possible that the process may be out of control. Figure 12-8 shows two examples of a process that can be out of control even though all values fall within the control limits.
Type II errors (or false negatives) occur when you conclude a process is in control when it’s actually out of control. That is, even if all values on your control charts are within the control limits, it’s still possible that the process may be out of control. Figure 12-8 shows two examples of a process that can be out of control even though all values fall within the control limits.

Illustration by Wiley, Composition Services Graphics
Figure 12-8: Out-of-control process.
Graph A in Figure 12-8 shows a run — a trend of five or more observations that are either going up or going down — which can indicate the process is out of control (even if all points are within the control limits). Tool wear and other machine-based functioning issues can cause performance to trend in one direction. In this case, an operations manager needs to take action to correct the trend.
If five or more observations are above or below the mean, which is the situation that’s shown in Graph B of Figure 12-8, then this also indicates that the process may also be out of control; you should investigate to find out what in the process has changed to cause the mean to shift.

 Moreover, a customer doesn’t usually define the quality of a product or service by a single metric. Instead, quality is defined across a range of dimensions. According to David Garvin of the Harvard Business School, these are the attributes that customers most commonly consider when defining quality:
Moreover, a customer doesn’t usually define the quality of a product or service by a single metric. Instead, quality is defined across a range of dimensions. According to David Garvin of the Harvard Business School, these are the attributes that customers most commonly consider when defining quality: In the worst case, whether it’s a runaway automobile, a spontaneously combusting computer battery, or a child’s toy that becomes a choking hazard, external failures can cause serious injury to customers and incur litigation and liability costs — along with a severe blow to corporate reputation.
In the worst case, whether it’s a runaway automobile, a spontaneously combusting computer battery, or a child’s toy that becomes a choking hazard, external failures can cause serious injury to customers and incur litigation and liability costs — along with a severe blow to corporate reputation.