APPENDIX C
Decimal, binary and hexadecimal numbers
Homosapiens are used to Decimal numbers, i.e. 0,1,2,3 …… 9. Electronic machines or chips use Binary numbers 0 and 1, (OFF and ON).
Decimal numbers increase in tens, i.e. 267 means 7 ones, 6 tens and 2 hundreds.
![]()
Binary numbers increase in twos, i.e. 1010. The right hand 0 means no ones, the next digit means 1 two, the next means no fours, the next 1 eight etc.
![]()
The binary number 1010 consists of 4 BInary digiTs it is called a 4 BIT number. 1010 is equivalent to 10 in decimal numbers.
We can change decimal numbers to binary and binary numbers to decimal. Digital systems, i.e. Computers are a little better than we are at this.
Consider the decimal number 89, to turn this into a binary number write the binary scale:
128 64 32 16 8 4 2 1
To make 89 we need (0 × 128) + (1 × 64) + (0 × 32) + (1 × 16) + (1 × 8) + (0 × 4) + (1 × 2) + (1 × 1).
So 89 in decimal = 01011001 in binary.
To convert a binary number to decimal add up the various multiples of 2, i.e. 10011010 is:
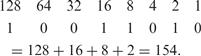
A long string of binary numbers is difficult to read, i.e. 11010101 to make this shorter and therefore easier to put into a microcontroller Hexadecimal numbers are used. Hexadecimal numbers increase in sixteen's and are described by sixteen digits. Table C.1 shows these 16 digits and their decimal and binary equivalents.
Table C.1 4 BIT Decimal, binary and hexadecimal representation
| Decimal | Binary | Hexadecimal |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
The PIC microcontrollers are 8 bit micros, they use 8 binary digits for number representation like
10010101 this is
![]()
The largest decimal number that can be represented by an 8 bit number is:
11111111 which represents:-
![]()
But we can program our microcontroller to increase our number representation from 8 bits i.e. up to 255:
to 16 bits, numbers up to 65,535
to 24 bits, numbers up to 16,777,215
to 32 bits, numbers up to 4,294,967,295 etc.
As mentioned earlier hexadecimal numbers are a shorter way of writing binary numbers. To do this divide the binary number into groups of 4 and write each group of 4 as a hex number.
i.e. 10010110 as 1001 0110 in binary
= 9 6 in hex.
i.e. 11011010 as 1101 1010 in binary
= D A in hex.
Table C.2 shows some of the 255 numbers represented by 8 bits.
Table C.2 8 BIT Decimal, binary and hexadecimal representation
| Decimal | Binary | Hexadecimal |
| 0 | 00000000 | 00 |
| 1 | 00000001 | 01 |
| 2 | 00000010 | 02 |
| 3 | 0000011 | 03 |
| 4 | 00000100 | 04 |
| 5 | 00000101 | 05 |
| 8 | 00001000 | 08 |
| 15 | 00001111 | 0F |
| 16 | 00010000 | 10 |
| 31 | 00011111 | 1F |
| 32 | 00100000 | 20 |
| 50 | 00110010 | 32 |
| 63 | 00111111 | 3F |
| 64 | 01000000 | 40 |
| 100 | 01100100 | 64 |
| 127 | 01111111 | 7F |
| 128 | 10000000 | 80 |
| 150 | 10010110 | 96 |
| 200 | 11001000 | C8 |
| 250 | 11111010 | FA |
| 251 | 11111011 | FB |
| 252 | 11111100 | FC |
| 253 | 11111101 | FD |
| 254 | 11111110 | FE |
| 255 | 11111111 | FF |
