8.2. Interaction of Elastic-Plastic Particles

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

8.2. Interaction of Elastic-Plastic Particles

8.2.1. Yield

In many industrial processes, particles are subject to high forces or impact at high speeds, as a consequence of which plastic deformation can take place. To define the onset of plastic deformation, the theory of plasticity introduces two yield criteria:

1. The von Mises yield criterion, in which plastic deformation is initiated when the distortion energy exceeds the distortion energy for yield in simple tension, i.e., when the second invariant J₂ of the stress deviator tensor (s_ij) reaches a critical value:

$J_{2} = \frac{1}{2} s_{i j} s_{i j} = \frac{1}{6} [{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}] = k^{2} = \frac{Y^{2}}{3}$ $J_{2} = \frac{1}{2} s_{i j} s_{i j} = \frac{1}{6} [{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}] = k^{2} = \frac{Y^{2}}{3}$

(8.76)

where σ₁, σ₂, and σ₃ are the principal stresses in the state of complex stress, and k and Y are the yield stress in simple shear and in simple tension, respectively.

2. The Tresca criterion, which states that plastic deformation occurs when the maximum shear stress reaches the same value as the maximum shear stress for yield under simple tension,

$\max {\begin{matrix} | σ_{1} - σ_{2} |, & | σ_{2} - σ_{3} |, & | σ_{3} - σ_{1} | \end{matrix}} = 2 k = Y$ $\max {\begin{matrix} | σ_{1} - σ_{2} |, & | σ_{2} - σ_{3} |, & | σ_{3} - σ_{1} | \end{matrix}} = 2 k = Y$

(8.77)

For axisymmetric contacts between two spheres with Poisson's ratio υ = 0.3, both the von Mises and Tresca criteria predict that plastic deformation starts when (Johnson, 1985)

$p_{y 0} = 1.60 Y$ $p_{y 0} = 1.60 Y$

(8.78)

where p_y0 is the maximum contact pressure at the initiation of plastic deformation. In terms of the mean contact pressure p_ym, plastic deformation starts to occur when (Tabor, 1951)

$p_{ym} = 1.10 Y$ $p_{ym} = 1.10 Y$

(8.79)

8.2.2. Contact Pressure

The solution for a Hertz contact remains valid until plastic deformation occurs in one or both particles, depending on their yield strengths. Yield will first develop inside the particle at some distance from the center of the contact surface and a small amount of plastic flow occurs within the larger elastic region around it (Tabor, 1951). With further increase of the load and contact pressure, the plastic zone gradually reaches the contact surface, and eventually the whole of the material around the contact area undergoes plastic deformation (see Fig. 8.15). This implies that during the overall process the deformation changes from purely elastic to elastic-plastic and then to fully plastic. Thus, the contact deformation process can be divided into three phases:

Figure 8.15 The plastic deformation process during the compression of a spherical particle into a plastic solid: (a) the onset of plastic deformation which starts beneath the surface; (b) the plastic zone expands to the contact surface and fully plastic deformation occurs.

1. Elastic: the deformations of both contacting particles are elastic and the Hertz theory (Section 8.1.1) is still applicable;

2. Elastic-plastic: this is a transitional phase from purely elastic to fully plastic. It begins once plastic deformation occurs in the particle and terminates in the fully plastic phase;

3. Fully plastic: this becomes dominant once the plastic zone reaches the surface and the material surrounding the contact area undergoes plastic deformation.

Note that for contacts between two elastic-plastic particles, plastic deformation will normally be initiated first in the particle with the lower yield strength, but as the contact deformation proceeds, the maximum contact pressure increases and, as soon as it exceeds 1.60Y in the other particle, this begins to deform plastically as well. As a result, both particles will be permanently deformed.

For contacts between elastic bodies, or elastic-plastic bodies within the elastic region, the contact pressure can be determined using Hertz theory as discussed in Section 8.1.1. A solution for a fully plastic contact was obtained using the slip line method by Tabor (1951), who suggested that the pressure over the contact area is not uniform but is somewhat higher in the center than at the edge. The mean contact pressure p_m for a fully plastic contact is

$p_{m} = 2.8 Y \sim 3.0 Y$ $p_{m} = 2.8 Y \sim 3.0 Y$

(8.80)

An expanding cavity model was proposed to describe the contact pressure in the transitional elastic-plastic phase, i.e., from elastic to fully plastic (see Johnson, 1985; Hill, 1950). The expanding cavity model assumes that, if the contact area has a diameter d = 2a, the contact surface is encased in a hemispherical core of radius a. Within the core, the material is under hydrostatic pressure of the same value as the mean contact pressure p_m. Plastic deformation will not take place in the material under hydrostatic pressure. Outside the core, the material behaves like an elastic-plastic body with a spherical cavity subject to a pressure p_m. From the boundary of the core, plastic deformation spreads into the surrounding material, and the plastic strains gradually diminish until they match the elastic strains at some radius c (c > a), at which the plastic-elastic boundary lies. Johnson (1985) showed that the pressure in the hydrostatic core is a function of the critical parameter

(E^{*} / Y) (a / R^{*})

$(E^{*} / Y) (a / R^{*})$

for a spherical particle of radius R:

$\frac{p_{m}}{Y} = \frac{2}{3} {1 + \ln [\frac{1}{3} \frac{E^{*}}{Y} \frac{a}{R^{*}}]}$ $\frac{p_{m}}{Y} = \frac{2}{3} {1 + \ln [\frac{1}{3} \frac{E^{*}}{Y} \frac{a}{R^{*}}]}$

(8.81)

Figure 8.16 illustrates how the mean contact pressure increases from p_m ∼ 1.1Y (the onset of plastic deformation) to ∼3.0Y (fully plastic deformation) as the size of the contact

a / R^{*}

$a / R^{*}$

increases, based on the prediction of Eq. (8.81). Fully plastic deformation occurs at a value of

E^{*} a / Y R^{*} \approx 40

$E^{*} a / Y R^{*} \approx 40$

, which is about 16 times greater than the value for the occurrence of yield.

The typical pressure distribution involving plastic deformation obtained from FEA (Wu et al., 2005) is shown in Fig. 8.17. It can be seen from Fig. 8.17(a) that the pressure distribution can be predicted using the Hertz theory when the maximum pressure p₀ is lower than 1.6Y. When p₀ is greater than 1.6Y, the pressure profile becomes significantly flattened, which is caused by plastic deformation. The maximum pressure remains approximately constant at 2.7∼3.0 times the yield stress Y once the flattened pressure profile is fully established.

Figure 8.16 The variation of p_m/Y with E^∗a/YR^∗ for the contact of elastic-plastic particles (Johnson, 1985).

Figure 8.17 Evolution of contact pressure distributions during the impact of an elastic sphere with an elastic-perfectly plastic substrate (V_i = 30 m/s) at various time instants during (a) compression and (b) restitution, obtained from FEA. The solid line in (a) is obtained from the Hertz theory, while those in (b) are predictions of Eq. (8.82) (Wu et al., 2005).

Mesarovic and Johnson (2000) derived an analytical expression for the contact pressure distribution during unloading:

$p_{(r)} = \frac{2 p^{*}}{π} \sin^{- 1} {[\frac{a^{2} - r^{2}}{a^{* 2} - r^{2}}]}^{1 / 2}$ $p_{(r)} = \frac{2 p^{*}}{π} \sin^{- 1} {[\frac{a^{2} - r^{2}}{a^{* 2} - r^{2}}]}^{1 / 2}$

(8.82)

where p^∗ and a^∗ are the pressure and contact radius at the end point of loading or the starting point of unloading. Figure 8.17b shows the evolution of the contact pressure distribution during unloading, in which the predictions of Eq. (8.82) using p^∗ = 2.8Y and a^∗ = 2.68 μm, obtained from the best fit to the FEA data, are also superimposed. It is clear that Eq. (8.82) can satisfactorily predict the pressure distribution during unloading of elastic-plastic spheres.

8.2.3. Contact Force–Displacement Relationship

The contact force–displacement relationship is crucial for understanding the interaction of elastic-plastic particles. The analytical derivation of the contact force–displacement relationship should be based on the determination of both the contact pressure distribution and the relationship between the relative approach and the contact radius. For fully plastic contact, it is generally accepted that the mean contact pressure is constant (2.8–3.0Y), and the relative approach is related to the contact radius by α = a²/2R^∗ provided that plastic deformation is small (see Johnson, 1985; Tabor, 1951). The force–displacement relationship can hence be determined.

For the transition regime from purely elastic to fully plastic contact (i.e., the elastic-plastic regime), an accurate determination of the contact pressure distribution and the relationship between relative approach and contact radius becomes more complicated. Bitter (1963) assumed that, once plastic deformation is initiated, the pressure becomes constant and the area that is loaded to that constant pressure increases upon further increase in the relative approach. A flattened contact pressure distribution obtained by truncating the Hertzian pressure profile was then proposed by Thornton (1997) and Thornton and Ning (1998), who also assumed that the Hertzian substitution a² = R^∗α is still valid for the elastic-plastic regime.

Figure 8.18 shows the typical time evolutions of the contact force and corresponding force–displacement relationship during impacts at various impact velocities. For impact at higher impact velocities, greater maximum contact forces and shorter durations of impact are obtained (see Fig. 8.18(a)). It is also interesting to note that the duration of compression slightly reduces with increasing impact velocity owing to the decrease in the duration for elastic compression at higher impact velocity. The restitution phase is essentially elastic and its duration decreases with increasing impact velocity as indicated by Eq. (8.15).

In Fig. 8.18(b), the corresponding contact force F is plotted against displacement α. The Hertz theory prediction is also superimposed in this figure. It can be seen that, in the elastic impact region, the loading curves obtained from the theoretical and numerical methods are almost identical. However, when plastic deformation occurs, the contact force–displacement curve diverges from the Hertz theory. The loading curves exhibit an upward curvature followed by a nearly constant slope at large displacements, which is consistent with the experimental observations of Goldsmith and Lyman (1960). A stiffer initial slope of the unloading curves is observed for impact at a higher velocity.

Figure 8.18 (a) Time histories of contact force and (b) Contact force–displacement relationships obtained from FEA, for the impact of an elastic sphere with an elastic-perfectly plastic substrate at various impact velocities.

8.2.4. Coefficient of Restitution

When collision occurs between two elastic-plastic particles, if the initial kinetic energy is so high that plastic deformation initiates, the initial kinetic energy converts to:

1. energy associated with elastic deformation of the material (i.e. elastic strain energy);

2. energy associated with plastic deformation (plastic strain energy);

3. energy associated with elastic wave propagation.

Since plastic deformation is irreversible, only the elastic strain energy can be recovered as rebound kinetic energy. Some initial kinetic energy is thus dissipated by plastic deformation and stress wave propagation. Below a certain impact velocity, the energy dissipation due to plastic deformation and stress wave propagation is negligible. Hence the rebound velocity is almost the same as the initial impact velocity and the coefficient of restitution is close to unity. As the impact velocity is increased, more energy is dissipated due to both plastic deformation and elastic wave propagation, and the coefficient of restitution decreases.

Hutchings (1979) showed that only a few percent of the initial kinetic energy is normally dissipated by stress waves during plastic impacts. Where plastic deformation occurs, the energy associated with it is normally much larger than that associated with stress wave propagation. For example, for the impact of a hard steel sphere with a mild steel block at a velocity of about 70 m/s, the measured coefficient of restitution is about 0.4, in which only about 3% of the kinetic energy is dissipated by stress wave propagation.

Several theoretical models have been developed to predict the coefficient of restitution for the impact of elastic-plastic spheres. Thornton (1997) developed a theoretical model for the normal impact of two elastic-perfectly plastic spheres, in which a Hertzian pressure distribution with a cut-off was introduced. In addition, a constant cut-off pressure p_y was assumed during the loading. An analytical solution for the coefficient of restitution was obtained as follows,

$e_{n} = {(\frac{6 \sqrt{3}}{5})}^{1 / 2} {[1 - \frac{1}{6} {(\frac{v_{y}}{v_{ni}})}^{2}]}^{1 / 2} {[\frac{v_{y} / v_{ni}}{v_{y} / v_{ni} + 2 \sqrt{6 / 5 - (1 / 5) {(v_{y} / v_{ni})}^{2}}}]}^{1 / 4}$ $e_{n} = {(\frac{6 \sqrt{3}}{5})}^{1 / 2} {[1 - \frac{1}{6} {(\frac{v_{y}}{v_{ni}})}^{2}]}^{1 / 2} {[\frac{v_{y} / v_{ni}}{v_{y} / v_{ni} + 2 \sqrt{6 / 5 - (1 / 5) {(v_{y} / v_{ni})}^{2}}}]}^{1 / 4}$

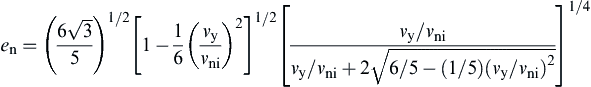(8.83)

where v_ni is the initial velocity and v_y is the impact velocity below which the contact deformation is elastic and is defined by

$v_{y} = {(\frac{π}{2 E^{*}})}^{2} {(\frac{8 π R^{* 3} p_{y}^{5}}{15 m^{*}})}^{1 / 2}$ $v_{y} = {(\frac{π}{2 E^{*}})}^{2} {(\frac{8 π R^{* 3} p_{y}^{5}}{15 m^{*}})}^{1 / 2}$

(8.84)

It should be noted that p_y and v_y do not represent the maximum contact pressure and the impact velocity at the instant when plastic deformation is initiated. Instead, they correspond to the instant when significant flattening of the contact pressure distribution commences (See Fig. 8.17(a)), and p_y ≈ 2.8Y (Thornton et al., 2001).

For impact dominated by fully plastic deformation, Johnson (1985) proposed a simplified model by introducing the following simplifications: (1) the relative approach is related to the contact radius by:

$α = \frac{a^{2}}{2 R^{*}}$ $α = \frac{a^{2}}{2 R^{*}}$

(8.85)

(2) the mean contact pressure p_m is constant and equal to 3.0Y. An expression for the coefficient of restitution e_n was obtained as

$e_{n}^{2} = \frac{3 \sqrt{2} π^{5 / 4}}{5} (\frac{p_{m}}{E^{*}}) {(\frac{\frac{1}{2} m^{*} v_{ni}^{2}}{p_{m} R^{* 3}})}^{- 1 / 4}$ $e_{n}^{2} = \frac{3 \sqrt{2} π^{5 / 4}}{5} (\frac{p_{m}}{E^{*}}) {(\frac{\frac{1}{2} m^{*} v_{ni}^{2}}{p_{m} R^{* 3}})}^{- 1 / 4}$

(8.86)

For the impact of a sphere with a surface, Eq. (8.86) reduces to

$e_{n} = 1.718 {(\frac{p_{m}^{5}}{E^{* 4} ρ})}^{1 / 8} v_{ni}^{- 1 / 4}$ $e_{n} = 1.718 {(\frac{p_{m}^{5}}{E^{* 4} ρ})}^{1 / 8} v_{ni}^{- 1 / 4}$

(8.87)

Equation (8.87) indicates that e_n is proportional to

v_{ni}^{- 1 / 4}

$v_{ni}^{- 1 / 4}$

Wu et al. (2003) systematically analyzed the impact of elastic-plastic particles using the finite element method. The coefficients of restitution obtained from numerical modeling of elastic-plastic impacts at various conditions are plotted against the normalized impact velocity v_ni/v_y in Fig. 8.19. This shows that the data for various impact cases follow a single master curve, implying that the coefficient of restitution depends primarily upon v_ni/v_y for impacts of elastic-perfectly plastic particles. A better fit to the data at high impact velocities (i.e., v_ni/v_y ≥ 100) gives:

$e_{n} = \bar{c} {(\frac{v_{ni}}{v_{y}})}^{- 1 / 4} where \bar{c} = 2.08$ $e_{n} = \bar{c} {(\frac{v_{ni}}{v_{y}})}^{- 1 / 4} where \bar{c} = 2.08$

(8.88)

as shown by the dashed line in Fig. 8.19. This is consistent with the prediction of Johnson (1985), see also Eq. (8.87).

Many experimental data for the collision of elastic-plastic spheres have also been reported in the literature (see, e.g., Tabor, 1948; Bridges et al., 1984; Labous et al., 1997). The experimental results for coefficient of restitution were reported by Tabor (1948) for cast steel and drawn brass balls with impact velocities up to 4.5 m/s, which are also plotted in Fig. 8.19. It is clear that the coefficient of restitution is not constant in general. Bridges et al. (1984) reported some experimental results on the coefficient of restitution for the collision of ice particles at impact velocities relevant to the formation of Saturn's rings, in order to understand ice-particle collision processes. They obtained the following empirical expression for the coefficient of restitution:

Figure 8.19 Coefficient of restitution as a function of v_ni/v_y0 for elastic-plastic impacts. FEA, finite element analysis.

$e_{n} = 0.32 v_{ni}^{- 0.23}$ $e_{n} = 0.32 v_{ni}^{- 0.23}$

(8.89)

for the range of impact velocity 0.015 cm/s < v_ni < 5.1 cm/s. The impact of two nylon spheres was experimentally investigated by Labous et al. (1997) using a high-speed video system. The size and velocity dependences of the coefficient of restitution were investigated. It was suggested that there were two basic energy dissipation regimes: (i) plastic deformation at high impact velocities and (ii) visco-elastic dissipation at low impact velocities.

8.2.5. The Effect of Tangential Loading

For contacts of elastic-plastic particles with tangential loading, the effect of friction is to superimpose a stress induced by the tangential traction. This tangential traction alters the stresses in the contacting bodies and hence changes the loading condition at which plastic deformation is initiated. The stresses due to the combined effect of normal pressure and tangential traction in sliding contacts were analyzed by Johnson and Jefferis (1963), Hamilton and Goodman (1966), and Bryant and Keer (1982). The analysis showed that, due to the effect of friction, the point of maximum shear stress moves closer to the contacting surfaces. Both Tresca and von Mises yield criteria were adopted to determine the contact pressure for the onset of yield in sliding contacts by Johnson and Jefferis (1963). Their results showed that for low values of the coefficient of friction (μ ≤ 0.25 by the Tresca criterion and μ ≤ 0.3 by the von Mises criterion), the yield point is still reached at a position beneath the contact surface (see Fig. 8.15). For large values of μ, plastic deformation first occurs at the interface between the contacting bodies, rather than in the subsurface.

Due to the complexity of elastic-plastic contact behavior with tangential loading and oblique impact, theoretical analysis becomes very difficult and there is consequently little literature on this topic. Nevertheless, the kinematic model discussed in Section 8.1.6 is generic so it can be applied to oblique impacts with elastic-plastic particles, for which the normal coefficient of restitution e_n can be defined as discussed in Section 8.2.4.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 8.2. Interaction of Elastic-Plastic Particles

Create new playlist

Sign In

Sign Up

8.2. Interaction of Elastic-Plastic Particles

8.2.1. Yield

8.2.2. Contact Pressure

8.2.3. Contact Force–Displacement Relationship

8.2.4. Coefficient of Restitution

8.2.5. The Effect of Tangential Loading

Table of Contents for
8.2. Interaction of Elastic-Plastic Particles