Finite Element Modeling
Abstract
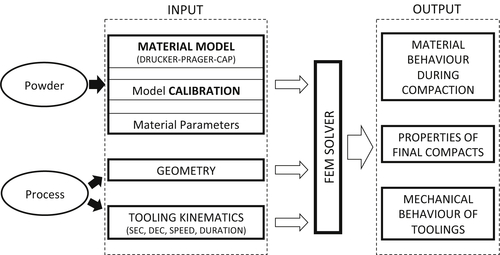
The finite element method (FEM) is used for modeling of physical systems in a wide variety of engineering disciplines, including structural dynamics, heat transfer, fluid dynamics, and aerodynamics. In this chapter, the application of FEM in modeling particle systems is introduced, which covers three aspects: (1) modeling of particle–particle interactions, (2) multiple particle finite element modeling (MPFEM), and (3) continuum modeling of powder compaction. A detailed discussion of the constitutive models used for powder compaction is presented, with particular reference to the Drucker–Prager-cap (DPC) model. In addition, methods for determination of material properties for finite element modeling with the DPC model are discussed in detail. Typical applications of FEM in modeling particle systems are illustrated.
Keywords
Contact modeling; Drucker–Prager-cap model; Finite discrete element method; Finite element modeling; Model calibration; Multiple particle finite element method; Particle interaction; Powder compaction10.1. Modeling of Particle–Particle Interaction
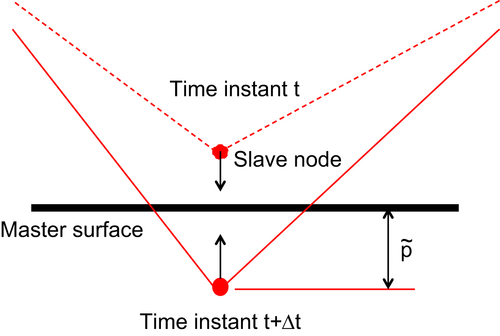
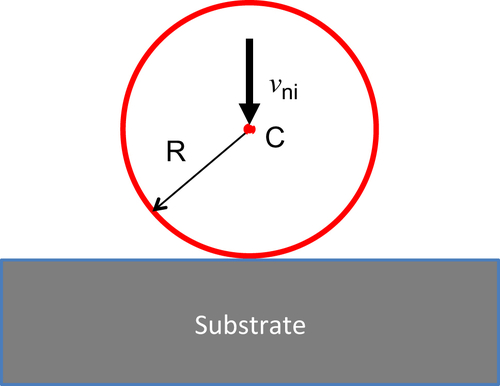
10.1.1. Contact Modeling Techniques
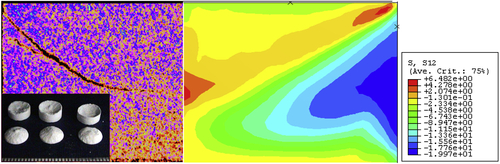
10.1.2. Applications
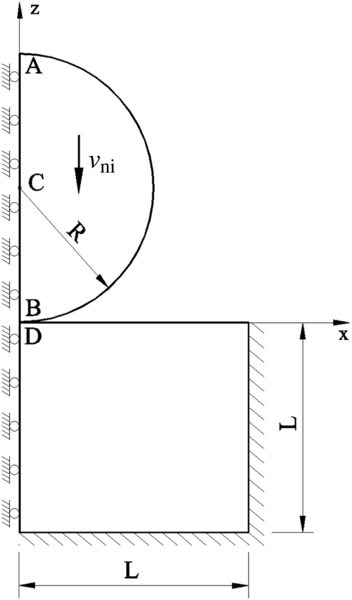



10.2. Multiple Particle Finite Element Modeling
![]() (10.2)
(10.2)



10.3. Continuum Modeling of Powder Compaction
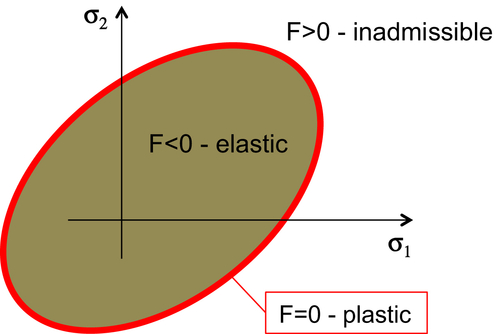
10.3.1. Material Models
![]() (10.3)
(10.3)
![]() (10.4)
(10.4)
![]() (10.5)
(10.5)
![]() (10.6)
(10.6)
![]() (10.7)
(10.7)
![]() (10.8)
(10.8)
![]() (10.9)
(10.9)
![]() (10.10)
(10.10)
![]() (10.11)
(10.11)
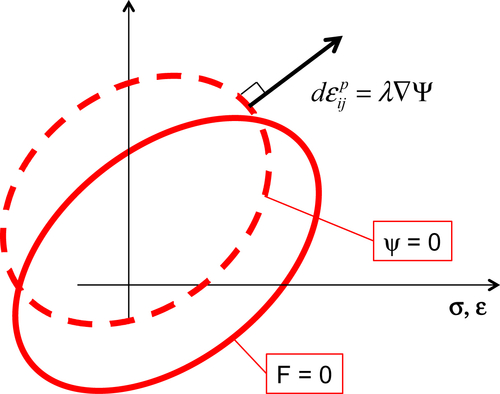
10.3.2. DPC Model
![]() (10.12)
(10.12)
![]() (10.13)
(10.13)
![]() (10.14)
(10.14)
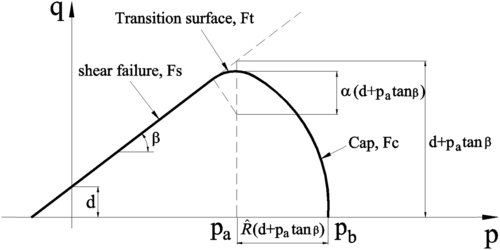
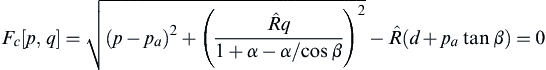 (10.15)
(10.15)
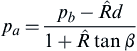 (10.16)
(10.16)
![]() (10.17)
(10.17)
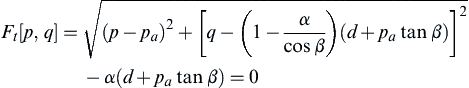 (10.18)
(10.18)
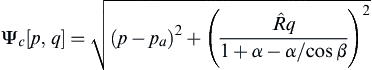 (10.19)
(10.19)
 (10.20)
(10.20)
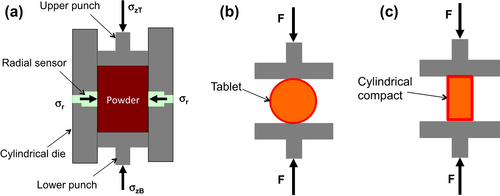
10.3.3. Determination of Constitutive Properties
10.3.3.1. Young’s modulus E and Poisson’s ratio υ
![]() (10.21)
(10.21)
![]() (10.22)
(10.22)

![]() (10.23)
(10.23)
![]() (10.24)
(10.24)
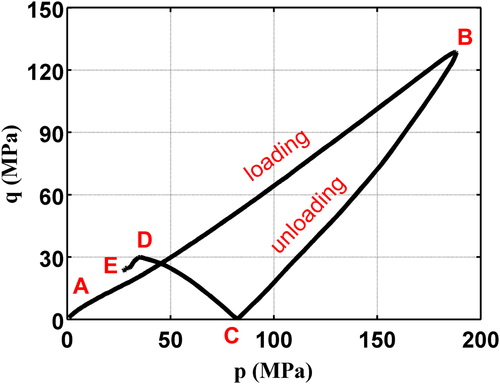
![]() (10.25a)
(10.25a)
![]() (10.25b)
(10.25b)
![]() (10.25c)
(10.25c)
![]() (10.26a)
(10.26a)
![]() (10.26b)
(10.26b)
![]() (10.27a)
(10.27a)
![]() (10.27b)
(10.27b)
10.3.3.2. Cohesion d and angle of friction β
![]() (10.28a)
(10.28a)
![]() (10.28b)
(10.28b)
![]() (10.29)
(10.29)
![]() (10.30a)
(10.30a)
![]() (10.30b)
(10.30b)
![]() (10.30c)
(10.30c)
![]() (10.31a)
(10.31a)
![]() (10.31b)
(10.31b)
![]() (10.32a)
(10.32a)
![]() (10.32b)
(10.32b)
![]() (10.33a)
(10.33a)
![]() (10.33b)
(10.33b)
![]() (10.34a)
(10.34a)
![]() (10.34b)
(10.34b)
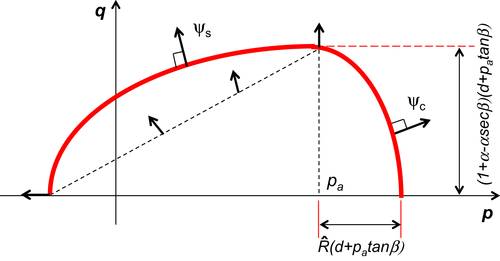
10.3.3.3. Cap parameters: 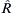 , pa, α, and pb
, pa, α, and pb
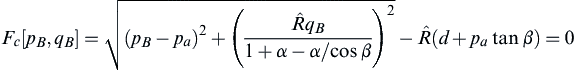 (10.35)
(10.35)
![]() (10.36)
(10.36)
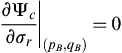 (10.37)
(10.37)
 (10.38)
(10.38)
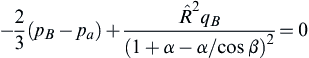 (10.39)
(10.39)
 (10.40)
(10.40)
 (10.41)
(10.41)
![]() (10.42)
(10.42)
![]() (10.43)
(10.43)
10.3.3.4. DPC model calibration procedure
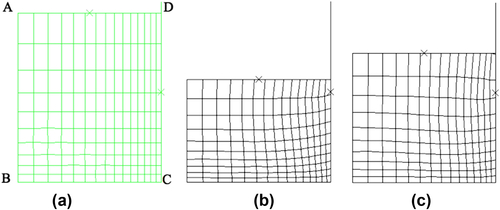
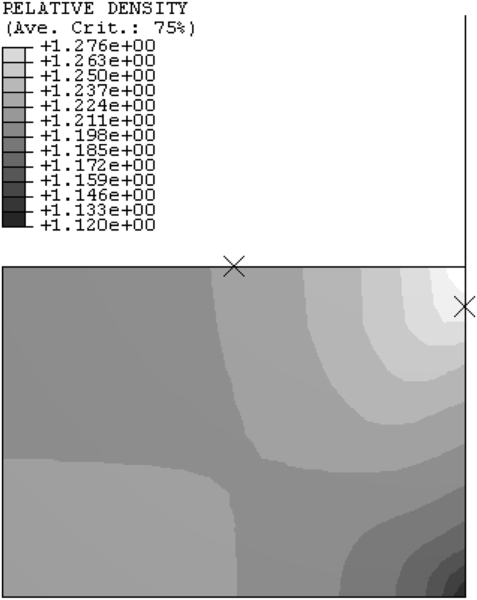
10.3.4. Modeling Procedure and Applications
Table 10.1
Density-Independent DPC Parameters Reported in the Literature
| Powder | E (GPa) | v | d (MPa) | β(o) | α | pb (MPa) | |
| α-Al2O3 (AKP-30), an agglomerated alumina powder (Aydin et al., 1996) | 9.03 | 0.28 | 5.50 | 16.50 | 0.03 | 0.56 | c1 = 3.07, c2 = 0.42, c3 = 7.34 |
| Lactose monohydrate (Wu et al., 2005) | 3.57 | 0.12 | 9.10 × 10−4 | 41.02 | 0.03 | 0.60 | c1 = 8.12 × 10−4, c2 = 9.05 |
| Lactose (Michrafy et al., 2002) | 4.60 | 0.17 | 0.46 | 29.30 | 0.03 | 0.058 | Column A in Table 10.2 |
| Distaloy AE, a steel powder (Bejarano et al., 2003) | k = 8.757 GPa n = 5 | 0.28 | 3.254 | 70.84 | 0.01 | 0.68 | 4.14 |
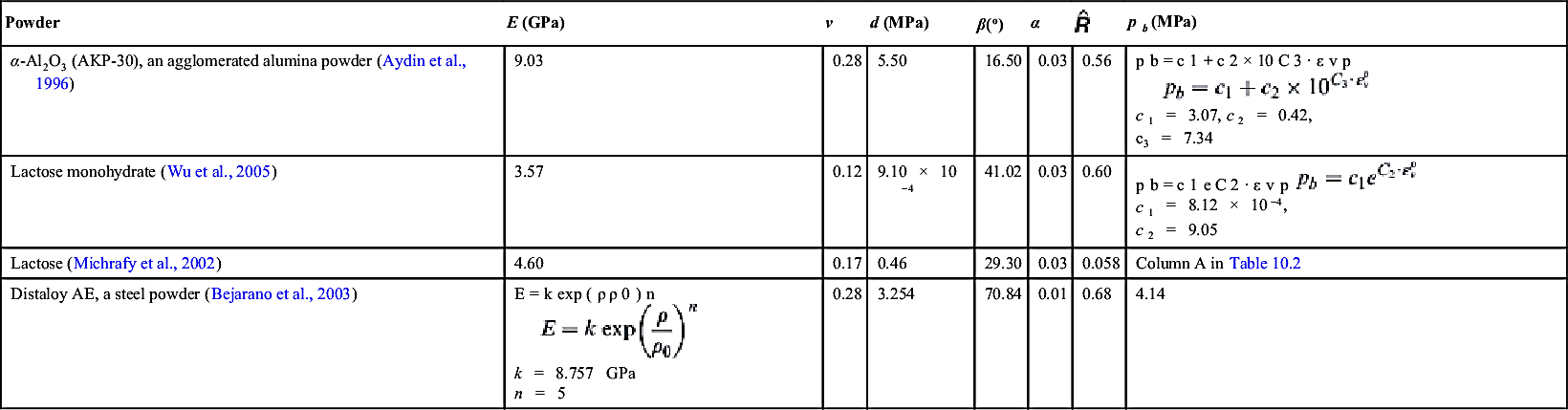
Table 10.2
The Variation of pb with ![]() Reported in Michrafy et al. (2002)
Reported in Michrafy et al. (2002)
| pb (MPa) | |
| 5.00 × 10−4 | 0.20 |
| 5.90 | 0.26 |
| 21.51 | 0.32 |
| 19.58 | 0.37 |
| 29.02 | 0.41 |
| 56.64 | 0.48 |
| 97.93 | 0.55 |
| 145.84 | 0.62 |
| 227.72 | 0.64 |
| 239.28 | 0.65 |
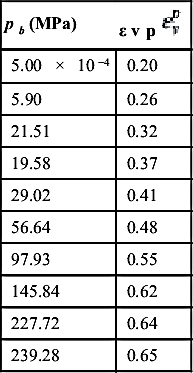
Table 10.3
DPC Parameters for MCC PH 102 from Cunningham et al. (2004): α = 0.03
| Relative Density | E (GPa) | v | d (MPa) | β (°) | |
| 0.30 | 0.50 | 0.02 | 0.10 | 41.00 | 0.05 |
| 0.35 | 0.55 | 0.03 | 0.20 | 46.00 | 0.08 |
| 0.40 | 0.60 | 0.04 | 0.30 | 48.00 | 0.11 |
| 0.45 | 0.70 | 0.05 | 0.50 | 52.00 | 0.13 |
| 0.50 | 0.80 | 0.07 | 0.70 | 54.00 | 0.16 |
| 0.55 | 0.90 | 0.08 | 1.10 | 57.00 | 0.20 |
| 0.60 | 1.20 | 0.10 | 1.50 | 58.00 | 0.25 |
| 0.65 | 2.00 | 0.12 | 2.00 | 61.00 | 0.32 |
| 0.70 | 2.50 | 0.14 | 2.60 | 63.00 | 0.39 |
| 0.75 | 3.00 | 0.17 | 3.30 | 65.00 | 0.45 |
| 0.80 | 4.00 | 0.20 | 4.20 | 66.00 | 0.51 |
| 0.85 | 4.60 | 0.23 | 5.30 | 68.00 | 0.58 |
| 0.90 | 6.50 | 0.26 | 6.60 | 71.00 | 0.65 |
| 0.95 | 8.50 | 0.29 | 8.20 | 72.00 | 0.75 |

Table 10.4
The Variation of pb with ![]() for MCC PH 102 from Cunningham et al. (2004): α = 0.03
for MCC PH 102 from Cunningham et al. (2004): α = 0.03
| pb (MPa) | εv |
| 0.043 | 0 |
| 0.62 | 0.12 |
| 1.61 | 0.26 |
| 2.59 | 0.37 |
| 4.08 | 0.48 |
| 6.87 | 0.57 |
| 12.00 | 0.66 |
| 16.80 | 0.74 |
| 23.70 | 0.81 |
| 31.80 | 0.88 |
| 42.30 | 0.95 |
| 56.60 | 1.01 |
| 79.60 | 1.07 |
| 119.00 | 1.12 |
| 143.00 | 1.14 |
Table 10.5
DPC Parameters for a steel Powder (Distaloy AE) from Shang et al. (2012)
| Relative Density | E (GPa) | v | d (MPa) | β (°) | |
| 0.57 | 9.64 | 0.19 | 0.59 | 71.31 | 0.48 |
| 0.61 | 13.50 | 0.16 | 0.98 | 70.97 | 0.48 |
| 0.65 | 15.81 | 0.16 | 1.64 | 70.63 | 0.50 |
| 0.69 | 19.86 | 0.15 | 2.70 | 70.82 | 0.52 |
| 0.71 | 22.56 | 0.15 | 3.63 | 70.83 | 0.53 |
| 0.75 | 30.08 | 0.14 | 6.55 | 70.67 | 0.56 |
| 0.78 | 37.22 | 0.12 | 8.41 | 70.50 | 0.58 |
| 0.80 | 39.72 | 0.12 | 10.20 | 70.33 | 0.60 |
| 0.82 | 45.90 | 0.12 | 12.93 | 70.51 | 0.62 |
| 0.83 | 51.68 | 0.11 | 15.12 | 69.99 | 0.63 |
| 0.85 | 55.73 | 0.11 | 17.78 | 70.52 | 0.65 |
| 0.86 | 60.36 | 0.11 | 20.24 | 70.17 | 0.67 |

Table 10.6
The Variation of pb with ![]() for a steel Powder (Distaloy AE) from Shang et al. (2012)
for a steel Powder (Distaloy AE) from Shang et al. (2012)
| pb (MPa) | εv |
| 2.63 | 0.00 |
| 9.33 | 0.33 |
| 18.88 | 0.42 |
| 31.07 | 0.49 |
| 41.52 | 0.54 |
| 54.61 | 0.59 |
| 71.19 | 0.64 |
| 93.89 | 0.70 |
| 111.36 | 0.74 |
| 134.07 | 0.78 |
| 150.68 | 0.80 |
| 172.52 | 0.83 |
| 204.87 | 0.86 |
| 229.35 | 0.88 |
| 250.34 | 0.90 |
| 278.32 | 0.92 |
| 298.44 | 0.93 |