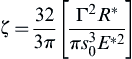8.3. Interaction of Particles with Adhesion

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

8.3. Interaction of Particles with Adhesion

8.3.1. Interaction Between Adhesive Rigid Spheres—Hamaker Theory

When two particles approach each other, interparticle attraction can result due to the van der Waals potential between the molecules of the two bodies. As a result, particles can adhere to each other, especially for fine particles, i.e., less than 100 μm. As discussed in detail in Seville et al. (1997), the van der Waals attractive potential for two molecules in vacuum can be given as

$W (r) = - \frac{C}{r^{6}}$ $W (r) = - \frac{C}{r^{6}}$

(8.90)

Using pair-wise addition, Hamaker (1937) analyzed the adhesive force between two rigid spherical particles at a separation distance s, for which the interaction energy is calculated by

$W = - \int_{V_{1}} \int_{V_{2}} \frac{C q^{2}}{r^{6}} ⅆ V_{1} ⅆ V_{2}$ $W = - \int_{V_{1}} \int_{V_{2}} \frac{C q^{2}}{r^{6}} ⅆ V_{1} ⅆ V_{2}$

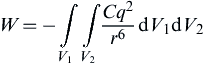(8.91)

where V₁ and V₂ are the volumes of the two particles and q is the number density of molecules in the solids (i.e., the number of molecules in a unit volume). Integration of Eq. (8.91) gives

$W (S) = - \frac{A R^{*}}{6 s}$ $W (S) = - \frac{A R^{*}}{6 s}$

(8.92)

where A (=π²Cq²) is the Hamaker constant, and R* is the effective radius defined in Eq. (8.6). Table 8.2 lists the typical values of Hamaker constant for the interaction of various materials in vacuum and in water.

Table 8.2

Hamaker Constants in Vacuum and Water of Various Inorganic Materials Interacting Against Four Materials at Room Temperature (Bergström, 1997)

Materials	Hamaker constant (10⁻²⁰ J)
	In Vacuum				In Water
	Silica	Silica Nitride	Alumina	Mica	Silica	Silica Nitride	Alumina	Mica
BaTiO₃	10.10	16.50	15.20	21.40	0.62	4.84	3.55	1.98
BeO	9.67	15.40	14.80	11.90	0.95	3.87	3.50	2.06
Diamond	13.70	22.00	21.10	17.00	1.71	7.94	7.05	4.03
CaCO₃	8.07	12.90	12.30	9.94	0.69	2.53	2.17	1.35
CaF₂	6.70	10.60	10.30	8.26	0.45	1.17	1.10	0.73
CdS	8.03	13.10	12.00	9.86	0.72	3.12	2.15	1.43
KCl	5.94	9.53	9.00	7.31	0.37	0.73	0.51	0.46
MgAl₂O₄	9.05	14.50	13.80	11.20	0.85	3.39	2.97	1.79
MgF₂	6.15	9.74	9.42	7.57	0.36	0.66	0.69	0.50
MgO	8.84	14.20	13.50	10.90	0.81	3.26	2.79	1.69
Mica	8.01	12.80	12.20	9.86	0.69	2.45	2.15	1.34
NaCl	6.45	10.30	9.77	7.93	0.44	1.17	0.88	0.66
PbS	5.37	8.88	7.90	6.57	−0.08	0.64	−0.20	−0.03
6H–SiC	12.60	20.30	19.20	15.50	1.52	7.22	6.05	3.54
β-Si₃N₄	10.80	17.30	16.50	13.30	1.17	5.13	4.43	2.61
SiO₂	7.59	12.10	11.60	9.35	0.63	2.07	1.83	1.16
SrTiO₃	9.44	15.40	14.20	11.60	0.57	4.02	2.98	1.69
TiO₂	9.46	15.40	14.20	11.60	0.69	4.26	3.11	1.83
Y₂O₃	9.24	14.90	14.00	11.40	0.89	3.80	3.11	1.89
ZnO	7.38	12.00	11.10	9.06	0.58	2.30	1.58	1.08
ZnS	9.69	15.70	14.60	11.90	1.02	4.56	3.55	2.19
3Y–ZrO₂	11.40	18.40	17.40	14.10	1.25	5.89	4.95	2.89

Hence the adhesive force between two particles can be obtained as

$F (s) = \frac{ⅆ W (s)}{ⅆ s} = \frac{A R^{*}}{6 s^{2}}$ $F (s) = \frac{ⅆ W (s)}{ⅆ s} = \frac{A R^{*}}{6 s^{2}}$

(8.93)

Equation (8.93) indicates that the adhesive force increases as the minimum separation distance decreases. It also implies that the adhesive force becomes infinite as the minimum separation distance approaches zero. Thus, Eq. (8.93) can only be applied up to a limit value of the minimum separation distance, i.e., a cut-off separation. Israelachvili (1991) suggested that a cut-off separation of 1.65 × 10⁻¹⁰ m gives a good approximation to the surface energies measured experimentally. This can be explained as follows: (1) the effect of surface roughness on the interaction will become significant when the separation between particles reduces below a certain value; (2) At small separations, the overlapped electron clouds associated with molecules leads to a very strong repulsion (see Fig. 8.20). The repulsive forces increase significantly as the separation distance decreases, so that the attractive force given in Eq. (8.93) can be balanced.

8.3.2. Interaction Between Adhesive Elastic Particles

In the Hamaker analysis discussed above, the particles are taken as rigid, i.e., the deformation induced by the attractive and repulsive forces is ignored. However, in reality, particles will deform as they are subjected to external forces, as shown in the earlier parts of this chapter, and the forces themselves will be modified by the resulting deformation. For this reason it is necessary to consider the deformation of particles in a full treatment of adhesive interaction. Therefore, theoretical models for normal and oblique interactions of elastic particles developed by Johnson et al. (1971) and Savkoor and Briggs (1977), respectively, are introduced in this section.

8.3.2.1. Normal Contact—JKR Theory

The JKR theory (Johnson et al., 1971) was developed as an extension of the Hertz theory for the contact of elastic spheres by considering surface adhesion at the interface. For the contact of two elastic spheres under a normal force F_n, if there is no surface adhesion, the contact radius a can be obtained from Eq. (8.12), i.e.,

Figure 8.20 The variation of potential energy with the separation between two particles attracted by van der Waals forces (s₀ denotes the equilibrium separation) (Seville et al., 1997).

$a^{3} = \frac{3 F_{n} R^{*}}{4 E^{*}}$ $a^{3} = \frac{3 F_{n} R^{*}}{4 E^{*}}$

(8.94)

If the two spheres are adhesive, an additional adhesive force will arise. As a result, the equilibrium contact area will increase. By introducing an equivalent Hertzian force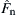

{\hat{F}}_{n}

${\hat{F}}_{n}$

(i.e. an augmented normal contact force that would produce the same contact area as the equilibrium contact area using the Hertz theory), Eq. (8.94) can be rewritten as

$a^{3} = \frac{{3 \hat{F}}_{n} R^{∗}}{{4 E}^{∗}}$ $a^{3} = \frac{{3 \hat{F}}_{n} R^{∗}}{{4 E}^{∗}}$

(8.95)

Johnson et al. (1971) showed that

${\hat{F}}_{n} = F_{n} + 6 π γ R^{*} \pm \sqrt{12 π γ R^{*} F_{n} + {(6 π γ R^{*})}^{2}}$ ${\hat{F}}_{n} = F_{n} + 6 π γ R^{*} \pm \sqrt{12 π γ R^{*} F_{n} + {(6 π γ R^{*})}^{2}}$

(8.96)

where γ is the energy per unit area of the surfaces in contact.

Substituting Eq. (8.96) into Eq. (8.95) and rearranging, an expression for the applied force F_n can be obtained as

$F_{n} = \frac{4 E^{*} a^{3}}{3 R^{*}} - 4 \sqrt{π γ E^{*} a^{3}}$ $F_{n} = \frac{4 E^{*} a^{3}}{3 R^{*}} - 4 \sqrt{π γ E^{*} a^{3}}$

(8.97)

The contact pressure distribution for the contact of two adhesive spheres can be given by the following equation (Johnson, 1976)

$p_{(r)} = \frac{3 {\hat{F}}_{n}}{2 π a^{2}} {[1 - {(\frac{r}{a})}^{2}]}^{1 / 2} - \frac{{\hat{F}}_{n} - F_{n}}{2 π a^{2}} {[1 - {(\frac{r}{a})}^{2}]}^{- 1 / 2}$ $p_{(r)} = \frac{3 {\hat{F}}_{n}}{2 π a^{2}} {[1 - {(\frac{r}{a})}^{2}]}^{1 / 2} - \frac{{\hat{F}}_{n} - F_{n}}{2 π a^{2}} {[1 - {(\frac{r}{a})}^{2}]}^{- 1 / 2}$

(8.98)

As shown by Johnson (1985), the first term of Eq. (8.98) results in a normal displacement over the contact area as

$μ_{i}^{'} = \frac{3 (1 - υ_{i}^{2}) {\hat{F}}_{n}}{8 E_{i} a^{3}} (2 a^{2} - r^{2})$ $μ_{i}^{'} = \frac{3 (1 - υ_{i}^{2}) {\hat{F}}_{n}}{8 E_{i} a^{3}} (2 a^{2} - r^{2})$

(8.99)

and the second term of Eq. (8.98) leads to the following uniform displacement over the contact area

$μ_{i}^{″} = - \frac{(1 - υ_{i}^{2}) ({\hat{F}}_{n} - F_{n})}{2 E_{i} a}$ $μ_{i}^{″} = - \frac{(1 - υ_{i}^{2}) ({\hat{F}}_{n} - F_{n})}{2 E_{i} a}$

(8.100)

where i = 1 or 2, denoting the contacting particles.

The relative approach of the two spheres can then be determined as

$α = μ_{1}^{'} + μ_{2}^{'} + μ_{1}^{″} + μ_{2}^{″} + \frac{r^{2}}{2 R^{*}} = \frac{3 {\hat{F}}_{n} (2 a^{2} - r^{2})}{8 E^{*} a^{3}} - \frac{{\hat{F}}_{n} - F_{n}}{2 E^{*} a} + \frac{r^{2}}{2 R^{*}}$ $α = μ_{1}^{'} + μ_{2}^{'} + μ_{1}^{″} + μ_{2}^{″} + \frac{r^{2}}{2 R^{*}} = \frac{3 {\hat{F}}_{n} (2 a^{2} - r^{2})}{8 E^{*} a^{3}} - \frac{{\hat{F}}_{n} - F_{n}}{2 E^{*} a} + \frac{r^{2}}{2 R^{*}}$

(8.101)

Substituting Eqs (8.96) and (8.97) into Eq. (8.101), the relative approach α can be expressed as a function of the contact radius a, i.e.,

$α = \frac{a^{2}}{R^{*}} - \sqrt{\frac{2 π γ a}{E^{*}}}$ $α = \frac{a^{2}}{R^{*}} - \sqrt{\frac{2 π γ a}{E^{*}}}$

(8.102)

When the applied force F_n is zero, solving Eq. (8.97) gives

$a_{0}^{3} = \frac{9 π γ {(R^{*})}^{2}}{E^{*}}$ $a_{0}^{3} = \frac{9 π γ {(R^{*})}^{2}}{E^{*}}$

(8.103)

For γ = 0, i.e., no adhesion between the two particles, a₀ becomes zero, as predicted by the Hertz theory. However, for adhesive contacts, i.e., γ ≠ 0, Eq. (8.103) gives a finite contact area (i.e., a₀ > 0). The contact area can be reduced when the applied load F_n becomes negative (i.e., a pulling force). In this case, to ensure that a real solution can be obtained from Eq. (8.96), the following condition has to be met:

${(F_{n} + 6 π γ R^{*})}^{2} - F_{n}^{2} \geq 0$ ${(F_{n} + 6 π γ R^{*})}^{2} - F_{n}^{2} \geq 0$

(8.104)

from which we have

$F_{n} \geq - 3πγ R^{*}$ $F_{n} \geq - 3πγ R^{*}$

(8.105)

Johnson et al. (1971) showed that the two spheres will separate if the applied pulling force reaches a critical value of F_c,

$F_{c} = - 3πγ R^{*}$ $F_{c} = - 3πγ R^{*}$

(8.106)

where F_c is referred to as the pull-off force. When F_n = −F_c, the contact radius a_c becomes

$a_{c}^{3} = \frac{3 F_{c} R^{*}}{4 E^{*}} = \frac{9 π γ R^{* 2}}{4 E^{*}}$ $a_{c}^{3} = \frac{3 F_{c} R^{*}}{4 E^{*}} = \frac{9 π γ R^{* 2}}{4 E^{*}}$

(8.107)

and the corresponding relative approach is given as

$α_{c} = [- {(\frac{4}{3})}^{1 / 3} + {(\frac{9}{16})}^{1 / 3}] {(\frac{F_{c}^{2}}{E^{* 2} R^{*}})}^{1 / 3} = - 0.275 {(\frac{F_{c}^{2}}{E^{* 2} R^{*}})}^{1 / 3}$ $α_{c} = [- {(\frac{4}{3})}^{1 / 3} + {(\frac{9}{16})}^{1 / 3}] {(\frac{F_{c}^{2}}{E^{* 2} R^{*}})}^{1 / 3} = - 0.275 {(\frac{F_{c}^{2}}{E^{* 2} R^{*}})}^{1 / 3}$

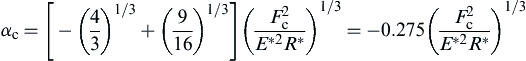(8.108)

For the contact of two adhesive elastic spheres, Johnson (1976) provided the following expression relating the contact force F_n to the relative approach α (Thornton and Ning, 1998):

$\frac{α}{α_{s}} = \frac{3 (\frac{F_{n}}{F_{c}}) + 2 \pm 2 {(1 + \frac{F_{n}}{F_{c}})}^{1 / 2}}{3^{2 / 3} {[(\frac{F_{n}}{F_{c}}) + 2 \pm 2 {(1 + \frac{F_{n}}{F_{c}})}^{1 / 2}]}^{1 / 3}}$ $\frac{α}{α_{s}} = \frac{3 (\frac{F_{n}}{F_{c}}) + 2 \pm 2 {(1 + \frac{F_{n}}{F_{c}})}^{1 / 2}}{3^{2 / 3} {[(\frac{F_{n}}{F_{c}}) + 2 \pm 2 {(1 + \frac{F_{n}}{F_{c}})}^{1 / 2}]}^{1 / 3}}$

(8.109)

where α_s is the relative approach when separation occurs.

$α_{s} = {(\frac{3 F_{c}^{2}}{16 E^{* 2} R^{*}})}^{1 / 3} = \frac{3}{2} {(\frac{π^{2} γ^{2} R^{*}}{2 E^{* 2}})}^{1 / 3}$ $α_{s} = {(\frac{3 F_{c}^{2}}{16 E^{* 2} R^{*}})}^{1 / 3} = \frac{3}{2} {(\frac{π^{2} γ^{2} R^{*}}{2 E^{* 2}})}^{1 / 3}$

(8.110)

The force–displacement relationship given in Eq. (8.109) is graphically illustrated in Fig. 8.21. It is worth mentioning that an alternative model for normal interaction of adhesive elastic spheres was developed by Derjaguin et al. (1975), which is known as the DMT theory. The difference between the JKR theory and the DMT theory is discussed in Box 8.3.

Figure 8.21 Force–displacement relationship for the contact of two adhesive spheres (Thornton and Ning, 1998).

Box 8.3 JKR Theory Versus DMT Theory (Lian, 1994)

In the DMT theory, it is assumed that the attractive force does not affect the deformation of the contacting surfaces. In addition, the DMT theory considers the adhesive force and Hertz theory separately, so that the contact area is determined by the Hertz theory and the adhesive force is only considered outside the contact area where the separation distance between surfaces is small. This is a different approach from the JKR theory which takes the adhesive force as acting within the contact area and contributing to the deformation of the contacting surfaces. So a larger contact area than that predicted by the Hertz theory is obtained (see Eqs (8.95) and (8.96)). In the DMT theory, no analytical expression for the adhesive force is available so that this needs to be obtained numerically. Nevertheless, the pull-off force is obtained as (Derjaguin et al., 1975)

$F_{c} = 4 π γ R^{*}$ $F_{c} = 4 π γ R^{*}$

(8.111)

which is similar to the JKR prediction but with a higher constant. There has been intense debate about the relative merits of the JKR and DMT theories. Tabor (1977) performed experiments with mica surfaces glued onto glass cylinders and examined the shape of the deformed surface and the way the surfaces separate. The experimental observations were more consistent with the analysis of the JKR theory than the DMT theory. Muller et al. (1980, 1983) revisited the DMT model and relaxed the assumption that the adhesive force does not change the contact deformation. This further analysis revealed that the pull-off force is a continuous function of a parameter ζ, with the DMT and JKR solutions as special cases. The parameter ζ is defined as

$ζ = \frac{32}{3 π} [\frac{Γ^{2} R^{*}}{π s_{0}^{3} E^{* 2}}]$ $ζ = \frac{32}{3 π} [\frac{Γ^{2} R^{*}}{π s_{0}^{3} E^{* 2}}]$

(8.112)

where s₀ is the equilibrium separation, Γ is the interfacial surface energy and given as

$Γ = \frac{A}{16 π s_{0}^{2}}$ $Γ = \frac{A}{16 π s_{0}^{2}}$

(8.113)

where A is the Hamaker constant. Muller et al. (1980) showed that the DMT theory holds for ζ ≪ 1, i.e., for hard solids of small radius and low surface energy, while the JKR theory is valid for ζ ≫ 1, i.e., for soft solid spheres of large radius and high surface energy. This was further confirmed experimentally by Cappella and Dietler (1999), who examined the interaction between the tip of an atomic force microscope probe and a sample, and found that the JKR theory can accurately predict the pull-off force for highly adhesive systems with a low stiffness and large tip radii, while the DMT model is valid for systems with low adhesion and small tip radii.

8.3.2.2. Normal Impact

According to the JKR theory (see Fig. 8.21), when two adhesive elastic spheres collide, as a result of the van der Waals forces a finite normal contact force will be induced at α = 0 (i.e., point A in Fig. 8.21). During the loading/compression phase, the velocity of the spheres decreases and the initial kinetic energy is converted into elastic energy stored in the deforming spheres (energy dissipation due to stress wave propagation is very small and can be ignored). When the velocity reduces to zero, the contact force reaches the maximum (point B in Fig. 8.21) and the compression stage terminates. During the restitution stage, the stored elastic energy is converted back to kinetic energy, enabling the spheres to move apart. When the relative approach returns to α = 0, all stored kinetic energy is recovered. However, the spheres remain sticking to each other. Further work needs to be done to separate them. As shown in Fig. 8.21, separation occurs at point S and hence the work required to break the contact W_s can be determined (Thornton and Ning, 1998) as

$W_{s} = \int_{0}^{α_{s}} F_{n} ⅆ α$ $W_{s} = \int_{0}^{α_{s}} F_{n} ⅆ α$

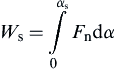(8.114)

Substituting Eqs (8.97) and (8.102) into Eq. (8.114) gives,

$W_{s} = \int_{a_{0}}^{a_{s}} (\frac{4 E^{*} a^{3}}{3 R^{*}} - 4 \sqrt{π γ E^{*} a^{3}}) (\frac{2 a}{R^{*}} - \sqrt{\frac{π γ}{E^{*} a}}) ⅆ a$ $W_{s} = \int_{a_{0}}^{a_{s}} (\frac{4 E^{*} a^{3}}{3 R^{*}} - 4 \sqrt{π γ E^{*} a^{3}}) (\frac{2 a}{R^{*}} - \sqrt{\frac{π γ}{E^{*} a}}) ⅆ a$

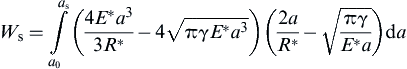(8.115)

In Eq. (8.115), when α = 0

$a = a_{0} = {(\frac{4 π γ R^{* 2}}{E^{*}})}^{1 / 3}$ $a = a_{0} = {(\frac{4 π γ R^{* 2}}{E^{*}})}^{1 / 3}$

(8.116)

When α = α_s,

$a = a_{s} = {[\frac{π γ R^{* 2}}{4 E^{*}}]}^{1 / 3}$ $a = a_{s} = {[\frac{π γ R^{* 2}}{4 E^{*}}]}^{1 / 3}$

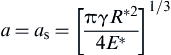(8.117)

Equation (8.115) can be integrated to obtain (Lian, 1994; Thornton and Ning, 1998)

$W_{s} = 14.18 {(\frac{γ^{5} R^{* 4}}{E^{* 2}})}^{1 / 3} = 0.936 F_{c} α_{s}$ $W_{s} = 14.18 {(\frac{γ^{5} R^{* 4}}{E^{* 2}})}^{1 / 3} = 0.936 F_{c} α_{s}$

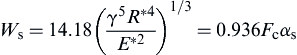(8.118)

During the impact, the only energy dissipated is the work done in separating the two spheres W_s. Therefore, applying an energy balance,

$\frac{1}{2} m^{*} v_{ni}^{2} - \frac{1}{2} m^{*} v_{nr}^{2} = W_{s}$ $\frac{1}{2} m^{*} v_{ni}^{2} - \frac{1}{2} m^{*} v_{nr}^{2} = W_{s}$

(8.119)

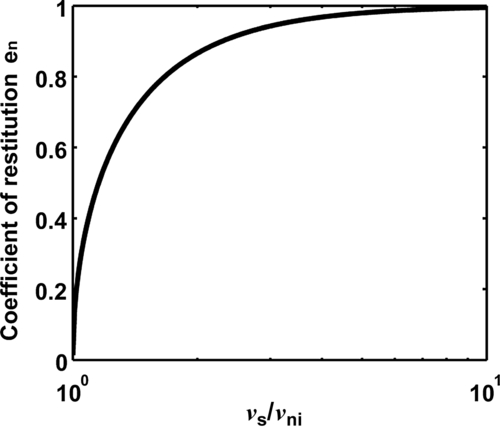
Equation (8.119) shows that when the two spheres adhere (i.e., are sticking), v_nr = 0, and the impact velocity v_ni = v_s, below which sticking takes place. Therefore, using Eqs (8.118) and (8.119), the sticking criterion can be obtained as

$v_{s} = {(\frac{14.18}{m^{*}})}^{1 / 2} {(\frac{γ^{5} R^{* 4}}{E^{* 2}})}^{1 / 6}$ $v_{s} = {(\frac{14.18}{m^{*}})}^{1 / 2} {(\frac{γ^{5} R^{* 4}}{E^{* 2}})}^{1 / 6}$

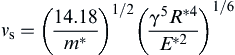(8.120)

If v_ni > v_s, the spheres will rebound and Eq. (8.119) can be rewritten as

$1 - {(\frac{v_{nr}}{v_{ni}})}^{2} = {(\frac{v_{s}}{v_{ni}})}^{2}$ $1 - {(\frac{v_{nr}}{v_{ni}})}^{2} = {(\frac{v_{s}}{v_{ni}})}^{2}$

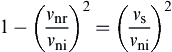(8.121)

Introducing the coefficient of restitution defined in Eq. (8.36), Eq. (8.121) can be rewritten as

$e_{n} = {[1 - {(\frac{v_{s}}{v_{ni}})}^{2}]}^{1 / 2}$ $e_{n} = {[1 - {(\frac{v_{s}}{v_{ni}})}^{2}]}^{1 / 2}$

(8.122)

The variation of e_n with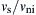

v_{s} / v_{ni}

$v_{s} / v_{ni}$

is presented in Fig. 8.22. It can be seen that the coefficient of restitution increases as the velocity ratio increases, and will approach unity if the velocity is sufficiently high.

8.3.2.3. Oblique Contact

The oblique interaction of adhesive elastic spheres was first analyzed by Savkoor and Briggs (1977), in which the JKR theory was extended to consider the tangential loading. They argued that, with the presence of adhesion, the tangential traction distribution in the contact area could be approximated with a “no-slip” solution of Mindlin (1949), i.e.,

Figure 8.22 Coefficient of restitution for the impact of two adhesive spheres.

$q_{(r)} = \frac{F_{t}}{2 π a} {(a^{2} - r^{2})}^{- 1 / 2} r \leq a$ $q_{(r)} = \frac{F_{t}}{2 π a} {(a^{2} - r^{2})}^{- 1 / 2} r \leq a$

(8.123)

in which the tangential force F_t is given by

$F_{t} = 8 G^{*} a δ$ $F_{t} = 8 G^{*} a δ$

(8.124)

It is further assumed that under the tangential force F_t the mechanical potential energy is −F_tδ and the elastic energy is F_tδ/2. Thus, the tangential force induces a reduction of the potential energy by

$U_{T} = - \frac{1}{2} F_{t} δ = - \frac{F_{t}^{2}}{16 G^{*} a}$ $U_{T} = - \frac{1}{2} F_{t} δ = - \frac{F_{t}^{2}}{16 G^{*} a}$

(8.125)

The total potential energy of the system then becomes

$U = U_{e} + U_{s} + U_{m} + U_{T} = - \frac{1}{2} F_{t} δ = \frac{1}{15} {[\frac{9}{16 E^{* 2} R^{*} {\hat{F}}_{n}}]}^{1 / 3} ({\hat{F}}_{n}^{2} - 5 {\hat{F}}_{n} F_{n} - 5 F_{n}^{2} - 30 π γ R^{*} {\hat{F}}_{n} - \frac{5 E^{*}}{4 G^{*}} F_{t}^{2})$ $U = U_{e} + U_{s} + U_{m} + U_{T} = - \frac{1}{2} F_{t} δ = \frac{1}{15} {[\frac{9}{16 E^{* 2} R^{*} {\hat{F}}_{n}}]}^{1 / 3} ({\hat{F}}_{n}^{2} - 5 {\hat{F}}_{n} F_{n} - 5 F_{n}^{2} - 30 π γ R^{*} {\hat{F}}_{n} - \frac{5 E^{*}}{4 G^{*}} F_{t}^{2})$

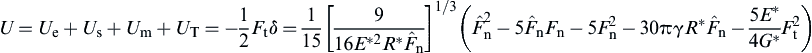(8.126)

The system reaches equilibrium when

\partial U / \partial {\hat{F}}_{n} = 0

$\partial U / \partial {\hat{F}}_{n} = 0$

, from which the equivalent Hertzian force can be obtained with a stable solution as

${\hat{F}}_{n} = F_{n} + 6 π γ R^{*} + \sqrt{{(F_{n} + 6 π γ R^{*})}^{2} - F_{n}^{2} - \frac{E^{*}}{4 G^{*}} F_{t}^{2}}$ ${\hat{F}}_{n} = F_{n} + 6 π γ R^{*} + \sqrt{{(F_{n} + 6 π γ R^{*})}^{2} - F_{n}^{2} - \frac{E^{*}}{4 G^{*}} F_{t}^{2}}$

(8.127)

Using Eq. (8.106), Eq. (8.127) can be rewritten as

${\hat{F}}_{n} = F_{n} + 2 F_{c} + \sqrt{4 F_{n} F_{c} + 4 F_{c}^{2} - \frac{E^{*}}{4 G^{*}} F_{t}^{2}}$ ${\hat{F}}_{n} = F_{n} + 2 F_{c} + \sqrt{4 F_{n} F_{c} + 4 F_{c}^{2} - \frac{E^{*}}{4 G^{*}} F_{t}^{2}}$

(8.128)

Substituting Eq. (8.128) into Eq. (8.95), the contact radius can then be determined as follows

$a^{3} = \frac{3 {\hat{F}}_{n} R^{*}}{4 E^{*}} = \frac{3 R^{*}}{4 E^{*}} (F_{n} + 2 F_{c} + \sqrt{4 F_{n} F_{c} + 4 F_{c}^{2} - \frac{E^{*}}{4 G^{*}} F_{t}^{2}})$ $a^{3} = \frac{3 {\hat{F}}_{n} R^{*}}{4 E^{*}} = \frac{3 R^{*}}{4 E^{*}} (F_{n} + 2 F_{c} + \sqrt{4 F_{n} F_{c} + 4 F_{c}^{2} - \frac{E^{*}}{4 G^{*}} F_{t}^{2}})$

(8.129)

It can be seen from Eq. (8.129) that the contact area decreases as the tangential force F_t increases. This is the so-called peeling mechanism proposed by Savkoor and Briggs (1977). They also suggested that the peeling process terminates when the tangential force F_t reaches

${\tilde{F}}_{t} = 4 \sqrt{\frac{G^{*}}{E^{*}} (F_{n} F_{c} + F_{c}^{2})}$ ${\tilde{F}}_{t} = 4 \sqrt{\frac{G^{*}}{E^{*}} (F_{n} F_{c} + F_{c}^{2})}$

(8.130)

If F_t exceeds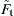

{\tilde{F}}_{t}

${\tilde{F}}_{t}$

, there is no real solution to Eq. (8.129). The corresponding contact radius at the critical tangential force is

${\tilde{a}}^{3} = \frac{3 R^{*}}{4 E^{*}} (F_{n} + 2 F_{c})$ ${\tilde{a}}^{3} = \frac{3 R^{*}}{4 E^{*}} (F_{n} + 2 F_{c})$

(8.131)

Equation (8.131) gives the smallest contact radius for oblique interaction of adhesive elastic spheres.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 8.3. Interaction of Particles with Adhesion

Create new playlist

Sign In

Sign Up

8.3. Interaction of Particles with Adhesion

8.3.1. Interaction Between Adhesive Rigid Spheres—Hamaker Theory

8.3.2. Interaction Between Adhesive Elastic Particles

8.3.2.1. Normal Contact—JKR Theory

8.3.2.2. Normal Impact

8.3.2.3. Oblique Contact

Table of Contents for
8.3. Interaction of Particles with Adhesion