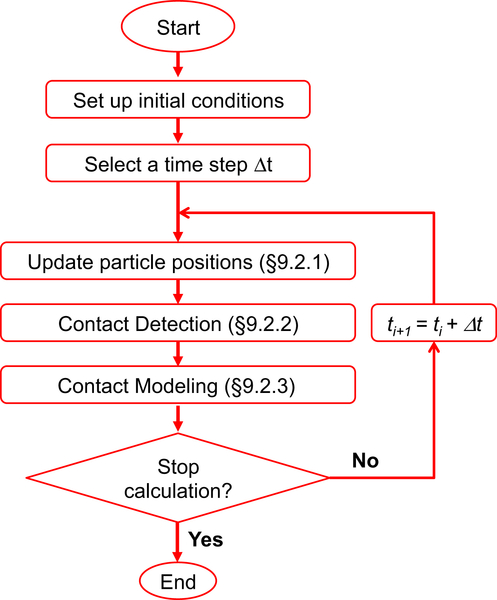
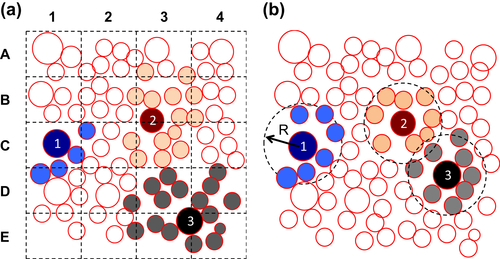
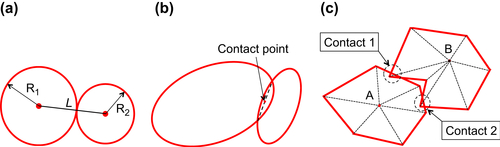
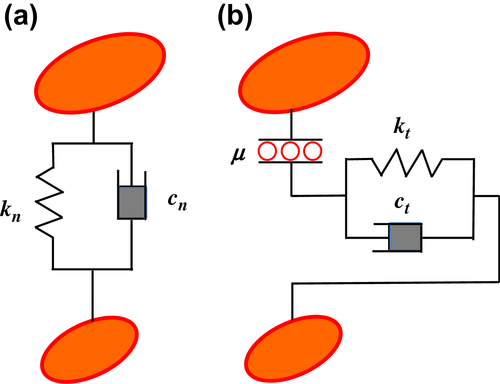
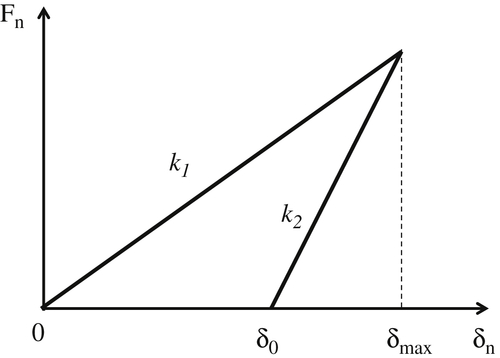
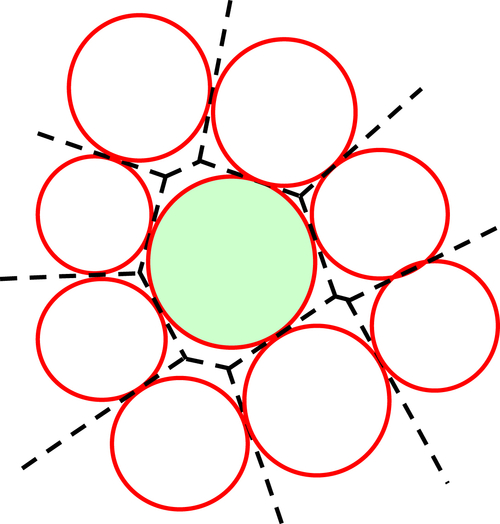
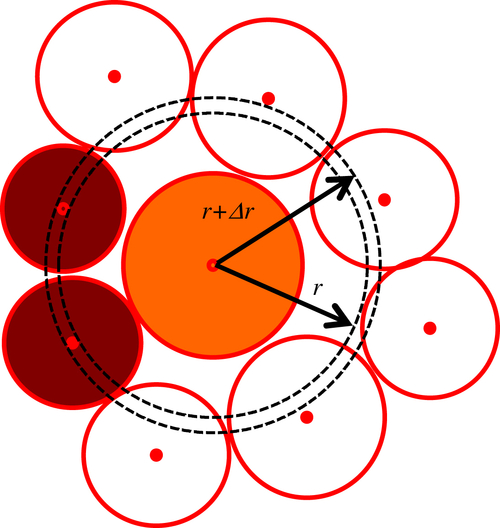
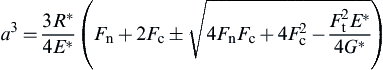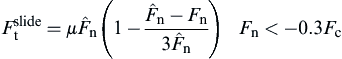Baxter J, Tüzün U, Burnell J, Heyes D.M. Granular dynamics simulations of two-dimensional heap formation. Physical Review E. 1997;55:3546–3554.
Bierwisch C, Kraft T, Riedel H, Moseler M. Three-dimensional discrete element models for the granular statics and dynamics of powders in cavity filling. Journal of the Mechanics and Physics of Solids. 2009;57:10–31.
Boon C.W, Houlsby G.T, Utili S. A new contact detection algorithm for three-dimensional non-spherical particles. Powder Technology. November 2013;248:94–102 ISSN:0032-5910.
Coube O, Cocks A.C.F, Wu C.Y. Experimental and numerical study of die filling, powder transfer and die compaction. Powder Metallurgy. 2005;48(1):68–76.
Cundall P.A, Hart R.P. Numerical modelling of discontinua. Engineering Computation. 1992;9:101–113.
Cundall P.A, Strack O.D.L. A discrete numerical model for granular assemblies. Géotechnique. 1979;29:47–65.
Cundall P.A. In: Satake M, Jenkins J.T, eds. Micromechanics of Granular Materials. Amsterdam: Elsevier; 1988:113–123.
Dury C.M, Knecht R, Ristow G.H. Size segregation of granular materials in a 3D rotating drum. High Perform. Computer Networks. 1998;1401:860–862.
Dziugys A, Peters B. An approach to simulate the motion of spherical and nonspherical fuel particles in combustion chambers. Granular Matter. 2001;3:231–265.
Fazekas S, Kertesz J, Wolf D.E. Piling and avalanches of magnetized particles. Physical Review E. 2005;71:061303.
Foerster S.F, Louge M.Y, Chang H, Allia K. Measurements of the collision properties of small spheres. Physics of Fluids. 1994;6(3):1108–1115.
German R.M, Park S.J. Handbook of Mathematical Relations in Particulate Materials Processing. London: Wiley; 2008.
Gorham D.A, Kharaz A.H. Measurement of particle rebound characteristics. Powder Technology. 2000;112:193–202.
Guo Y, Wu C.-Y, Kafui K.D, Thornton C. Numerical analysis of density-induced segregation during die filling. Powder Technology. 2009;197:111–119.
Guo Y, Kafui K.D, Wu C.-Y, Thornton C, Seville J.P.K. A coupled DEM/CFD analysis of the effect of air on powder flow during die filling. AIChE Journal. 2009;55(1):49–62.
Guo Y, Wu C.Y, Kafui K.D, Thornton C. Numerical analysis of density-induced segregation during die filling in the presence of air. Powder Technology. 2010;197(1–2):111–119.
Hunt K.H, Crossley F.R.E. Coefficient of restitution interpreted as damping in vibroimpact. Journal of Applied Mechanics. 1975;42(2):440–445.
Johnson K.L, Kendall K, Roberts A.D. Surface energy and the contact of elastic solids. Proceedings of the Royal Society of London. 1971;A 324:301–313.
Ketterhagen W.R, Curtis J.S, Wassgren C.R, Kong A, Narayan P.J, Hancock B.C. Granular segregation in discharging cylindrical hoppers: a discrete element and experimental study. Chemical Engineering Science. 2007;62:6423–6439.
Ketterhagen W.R, Curtis J.S, Wassgren C.R, Hancock B.C. Modeling granular segregation in flow from quasi-three-dimensional, wedge-shaped hoppers. Powder Technology. 2008;179:126–143.
Kohring G.A, Melin S, Puhl H, Tillemans H.J, Vermohlen W. Computer- simulations of critical, nonstationary granular flow—through a hopper. Computer Methods in Applied Mechanics and Engineering. 1995;124:273–281.
Kuo H.P, Knight P.C, Parker D.J, Tsuji Y, Adams M.J, Seville J.P.K. The influence of DEM simulation parameters on the particle behaviour in a V-mixer. Chemical Engineering Science. 2002;57:3621–3638.
Labous L, Rosato A.D, Dave R.N. Measurements of collisional properties of spheres using high-speed video analysis. Physical Review E. 1997;56:5717–5725.
Langston P.A, Nikitidis M.S, Tuzun U, Heyes D.M, Spyrou N.M. Microstructural simulation and imaging of granular flows in two- and three- dimensional hoppers. Powder Technology. 1997;94:59–72.
Lemieux A, Leonard G, Doucet J, Leclaire L.A, Viens F, Chaouki J, Bertrand F. Large-scale numerical investigation of solids mixing in a V-blender using the discrete element method. Powder Technology. 2008;181:205–216.
Li Y, Xu Y, Thornton C. A comparison of discrete element simulations and experiments for ‘sandpiles’ composed of spherical particles. Powder Technology. 2005;160:219–228.
Lin X, Ng T.T. Short communication; contact detection algorithms for three- dimensional ellipsoids in discrete element modelling. International Journal for Numerical and Analytical Methods in Geomechanics. 1995;19:653–659.
Lorenz A, Tuozzolo C, Louge M.Y. Measurements of impact properties of small, nearly spherical particles. Experimental Mechanics. 1997;37:292–298.
Luding S. Stress distribution in static two-dimensional granular model media in the absence of friction. Physical Review E. 1997;55:4720–4729.
Martin C.L, Bouvard D, Delette G. Discrete element simulations of the compaction of aggregated ceramic powders. Journal of the American Ceramic Society. 2006;89:3379–3387.
Matuttis H.G, Luding S, Herrmann H.J. Discrete element simulations of dense packings and heaps made of spherical and non-spherical particles. Powder Technology. 2000;109:278–292.
Mindlin R.D, Deresiewicz H. Elastic spheres in contact under varying oblique forces. Journal of Applied Mechanics. 1953;20:327–344.
Mindlin R.D. Compliance of elastic bodies in contact. Journal of Applied Mechanics. 1949;16:259–266.
Mishra B.K, Thornton C, Bhimji D. A preliminary numerical investigation of agglomeration in a rotary drum. Minerals Engineering. January 2002;15(1–2):27–33.
Mullier M.A, Seville J.P.K, Adams M.J. The effect of agglomerate strength on attrition during processing. Powder Technol. 1991;65:321.
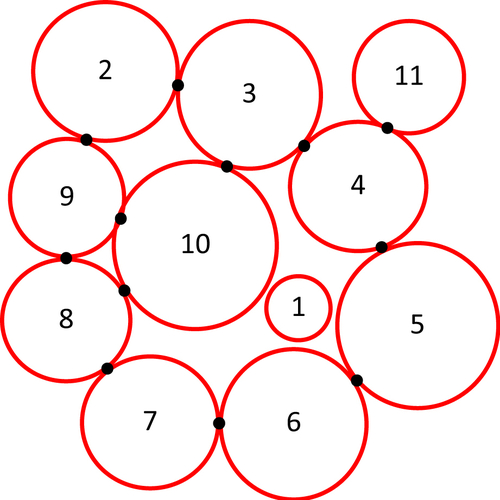
Ng T.T. Fabric study of granular materials after compaction. Journal of Engineering Mechanics. 1999;125:1390–1394.
Oda M, Konishi J, Nemat-Nasser S. Some experimentally based fundamental results on the mechanical behaviour of granular materials. Géotechnique. 1980;30(4):479–495.
Oda M. Co-ordination number and its relation to shear strength of granular materials. Soils and Foundations. 1977;17(2):29–42.
Ouadfel H, Rothenburg L. An algorithm for detecting inter-ellipsoid contacts. Computers and Geotechnics. 1999;24:245–263.
Pei C, Wu C.-Y, England D, Byard S, Berchtold H, Adams M. Numerical analysis of contact electrification using DEM–CFD. Powder Technology. 2013;248:34–43.
Pei C, Wu C.-Y, Adams M, England D, Byard S, Berchtold H. Contact electrification and charge distribution on elongated particles in a vibrating container. Chemical Engineering Science. 2014;125:238–247.
Pei C, Wu C.-Y, Adams M, England D, Byard S, Berchtold H. DEM-CFD modeling of particle systems with long-range electrostatic interactions. AIChE Journal. 2015;61:1792–1803.
Pei C, Wu C.-Y, Adams M. Numerical analysis of contact electrification of non-spherical particles in a rotating drum. Powder Technology. 2015;285:110–122.
Rock M, Morgeneyer M, Schwedes J, Brendel L, Wolf D.E, Kadau D. Visualization of shear motions of cohesive powders in the true biaxial shear tester. Particulate Science and Technology. 2008;26:43–54.
Satake M. Fabric tensor in granular materials. In: IUTAM Conference on Deformation and Failure of Granular Materials, Delft, 31 August–3 September. 1982:63–68.
Savkoor A.R, Briggs G.A.D. The effect of tangential force on the contact of elastic solids in adhesion. Proceedings of the Royal Society of London. 1977;A 356:103–114.
Smith L, Baxter J, Tüzün U, Heyes D.M. Granular dynamics simulations of heap formation: effects of feed rate on segregation patterns in binary granular heap. Journal of Engineering Mechanics. 2001;127:1000–1006.
Thornton C, Ning Z. A theoretical model for the stick/bounce behaviour of adhesive, elastic-plastic spheres. Powder Technology. 1997;99:154–162.
Thornton C, Randall W. In: Satake M, Jenkins J.T, eds. Micromechanics of Granular Materials. Amsterdam: Elsevier; 1988:133–142.
Thornton C, Yin K.K. Impact of elastic spheres with and without adhesion. Powder Technology. 1991;65:153–165.
Thornton C, Zhang L. Numerical simulations of the direct shear test. Chemical Engineering & Technology. 2003;26:153–156.
Thornton C, Zhang L. A numerical examination of shear banding and simple shear non-coaxial flow rules. Philosophical Magazine. 2006;86:3425–3452.
Thornton C, Cummins S.J, Cleary P.W. An investigation of the comparative behavior of alternative contact force models during elastic collisions. Powder Technology. 2011;210:189–197.
Thornton C, Cummins S.J, Cleary P.W. An investigation of the comparative behaviour of alternative contact force models during inelastic collisions. Powder Technology. 2013;233:30–46.
Thornton C. Interparticle sliding in the presence of adhesion. Journal of Physics D Applied Physics. 1991;24:1942–1946.
Thornton C. Special issue on numerical simulations of discrete particle systems. Powder Technology. 2000;109:3–265.
Thornton C. Special issue on discrete element modelling of fluidised beds. Powder Technology. 2008;184:132–265.
Thornton C. Special issue on the 4th Int. Conf. on Discrete Element Methods. Powder Technology. 2009;193:216–336.
Ting J, Khwaja M, Meachum L.R, Rowell J.D. An ellipse-based discrete element model for granular materials. International Journal for Numerical and Analytical Methods. 1993;17:603–623.
Ting J.M, Meachum L, Rowell J.D. Effect of particle shape on the strength and deformation mechanisms of ellipse-shaped granular assemblages. Engineering Computations. 1995;12:99–108.
Tsuji Y, Tanaka T, Ishida T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe. Powder Technology. 1992;71:239–250.
Tüzün U, Baxter J, Heyes D.M. Analysis of the evolution of granular stress- strain and voidage states based on DEM simulations. Philosophical Transactions of the Royal Society. 2004;A 362:1931–1951.
Walton O.R, Braun R.L. Viscosity, granular-temperature, and stress calculations for shearing assemblies of inelastic, frictional disks. Journal of Rheology. 1986;30:949–980.
Walton O.R. Numerical simulation of inclined chute flows of monodisperse inelastic, frictional spheres. Mechanics of Materials. 1993;16:239–247.
Wu C.Y, Cocks A.C.F, Gillia O.T, Thompson D.A. Experimental and numerical investigations of powder transfer. Powder Technology. 2003;138(2–3):214–226.
Wu C.Y, Cocks A.C.F. Numerical and experimental investigations of the flow of powder into a confined space. Mechanics of Materials. 2006;38(4):304–324.
Wu C.-Y. DEM simulations of die filling during pharmaceutical tableting. Particuology. 2008;6:412–418.
Wu C.-Y. Discrete Element Modelling Special issue for Powder Technology. London: Elsevier; 2012.
Wu C.-Y. Discrete Element Modelling of Particulate Media. RSC Publishing; 2012: 978-1-84973-503-2.
Yang R.Y, Zou R.P, Yu A.B. A simulation study of the packing of wet particles. AIChE Journal. 2003;49:1656–1666.
Yang R.Y, Zou R.P, Yu A.B, Choi S.K. Characterization of interparticle forces in the packing of cohesive fine particles. Physical Review E. 2008;78:031302.
Zeilstra C, van der Hoef M.A, Kuipers J.A.M. Simulation study of air-induced segregation of equal-sized bronze and glass particles. Physical Review E. 2006;74:010302(R).
Zeilstra C, van der Hoef M.A, Kuipers J.A.M. Simulation of density segregation in vibrated beds. Physical Review E. 2008;77:031309.
Zhang L, Thornton C. A numerical examination of the direct shear test. Géotechnique. 2007;57:343–354.
Zhang L. The Behaviour of Granular Material in Pure Shear, Direct Shear and Simple Shear (Ph.D. thesis). UK: Aston University; 2003.
Zhou Y.C, Xu B.H, Zou R.P, Yu A.B, Zulli P. Stress distribution in a sandpile formed on a deflected base. Advanced Powder Technology. 2003;14:401–410.
Zhu H.P, Zhou Z.Y, Yang R.Y, Yu A.B. Discrete particle simulation of particulate systems: theoretical developments. Chemical Engineering Science. 2007;62:3378–3396.
Zhu H.P, Zhou Z.Y, Yang R.Y, Yu A.B. Discrete particle simulation of particulate systems: a review of major applications and findings. Chemical Engineering Science. 2008;63:5728–5770.
![]() (9.1)
(9.1)![]() (9.2)
(9.2)![]() (9.3a)
(9.3a)![]() (9.3b)
(9.3b)![]() (9.4a)
(9.4a)![]() (9.4b)
(9.4b)![]() (9.5)
(9.5)![]() (9.20)
(9.20)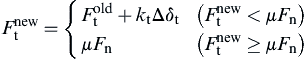 (9.21)
(9.21)![]() (9.22)
(9.22)![]() (9.23)
(9.23)![]() (9.24)
(9.24) (9.25)
(9.25)![]() (9.26)
(9.26)![]() (9.27)
(9.27)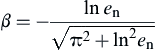 (9.28)
(9.28)![]() (9.29)
(9.29)![]() (9.30)
(9.30)![]() (9.31)
(9.31)![]() (9.32)
(9.32)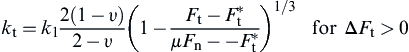 (9.33)
(9.33)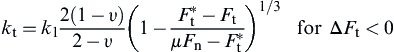 (9.34)
(9.34)![]() (9.35)
(9.35)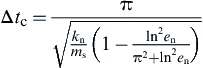 (9.36)
(9.36)![]() (9.37)
(9.37)![]() (9.38)
(9.38)
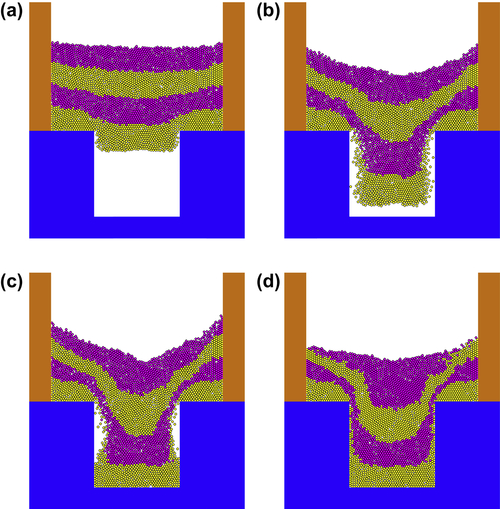


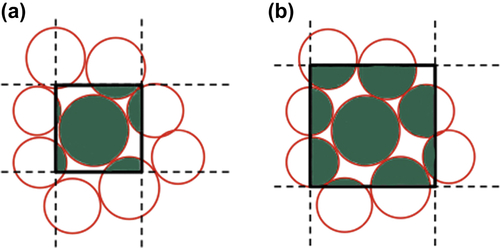

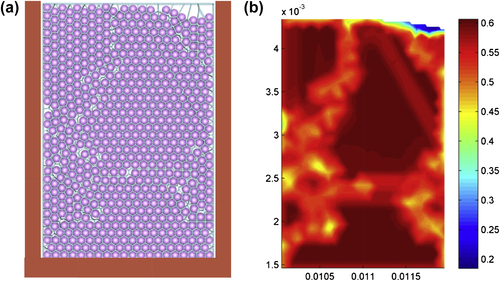
 (9.39)
(9.39)![]() (9.40)
(9.40)![]() (9.41)
(9.41)
![]() (9.42)
(9.42)![]() (9.43)
(9.43)![]() (9.44)
(9.44)![]() (9.45)
(9.45)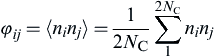 (9.46)
(9.46)![]() (9.47)
(9.47)
![]() (9.48)
(9.48)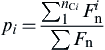 (9.49)
(9.49)