20. Sequential and Iterated Games

I have six locks on my door all in a row.

When I go out, I lock every other one.

I figure no matter how long somebody stands there picking the locks, they are always locking three.

—ELAYNE BOOSLER

Most board and video games are not like the prisoner’s dilemma, in which all players make one choice simultaneously and then the game is over. What if a player chooses before another player? What do the results of one game say about the future results of another? If a player is betrayed in one round of the prisoner’s dilemma, how should that affect her if she plays again? In this chapter, I cover games in which players make their choices in order to play games over and over again.

Game Trees

Matrices are insufficient when you are representing sequential games because a second player may behave differently once given the information the first player provides. You need some sort of diagram that shows this contingency. A game tree or decision tree is one way you can represent these kinds of games. These diagrams show branches for each outcome, such as the one in Figure 20.1 for a sequential game of the stag hunt.

Figure 20.1 Mario/Luigi’s stag hunt.

In Figure 20.1, play goes from left to right. The first parallelogram is a choice node in which Mario chooses to hunt Stag or Hare. Then, after he makes his choice, Luigi chooses to hunt Stag or Hare.

Solving these games can be similar to solving simultaneous games. Many of the principles are the same. First, the player making the decision cares only about his payoffs, so those payoffs should be the only criteria he evaluates when making a decision. Second, both players know their situations in the game. The only difference is that to solve this, you need to use a technique known as backwards induction.

Start with the rightmost decision. In this example, start with Luigi’s decision at the bottom, after he knows that Mario chose Hare. Luigi’s choice is between 0 pounds of meat if he chooses Stag, and 20 pounds of meat if he chooses Hare. It is obvious that Luigi will choose Hare. In fact, since Luigi will never choose the (Hare, Stag) node, you can remove it from your analysis.

Next, look at the other rightmost decision. If Luigi knows Mario has chosen Stag, Luigi’s choice is between getting 75 pounds of meat for choosing Stag or 20 pounds for choosing Hare. It’s again clear what Luigi will choose. He will choose Stag, so you can also remove the (Stag, Hare) node.

This simplifies the decision for Mario (Figure 20.2).

Figure 20.2 Removing the decisions Luigi would not make.

Now Mario’s decision is the only decision left. Should Mario take Stag or Hare? Since he receives more for Stag, he will take it and the game’s outcome will be (Stag, Stag).

Unlike the matrix version of this that had two likely solutions, this version has only one. In any sequential game like the one in Figure 20.1, with no simultaneous moves if each player’s payoffs are unique to that player, backwards induction always outputs a unique solution.

Sequential games and decisions allow you to analyze commitment problems. As a university instructor, I am bound by my institution’s policies to enforce academic honesty. If students are cheating, I must act. However, what if I had an option? Let’s examine all the options for me and all the options for a student:

• I can actually look for cheating or not.

• I can prosecute cheating if I find it or not.

• A student can choose to cheat or not.

Next, rank the preferences for this game. First, consider students who care only about the amount of work they have to do and not about their long-term educational future. Assume they would rather cheat than not, but only if they will not be caught. I would rather not spend my time looking for cheaters, but if cheaters exist, I would rather catch them than not.

Student’s preferences (with 1 being the best):

• Cheat and Don’t Get Caught

• Cheat, but Don’t Get Punished

• Do Work, Cheat, and Get Caught

Teacher preferences (with 1 being the best):

• Don’t Check and No Cheating

• Check and No Cheating

• Prosecute Cheater

• Don’t Prosecute Cheater

• Don’t Check and Student Cheats

You can depict this as a tree (Figure 20.3) where the professor lets the students know of the policy and the student has the freedom to choose to cheat or do her work. Assign 4 points for the best result down to 0 points for the worst.

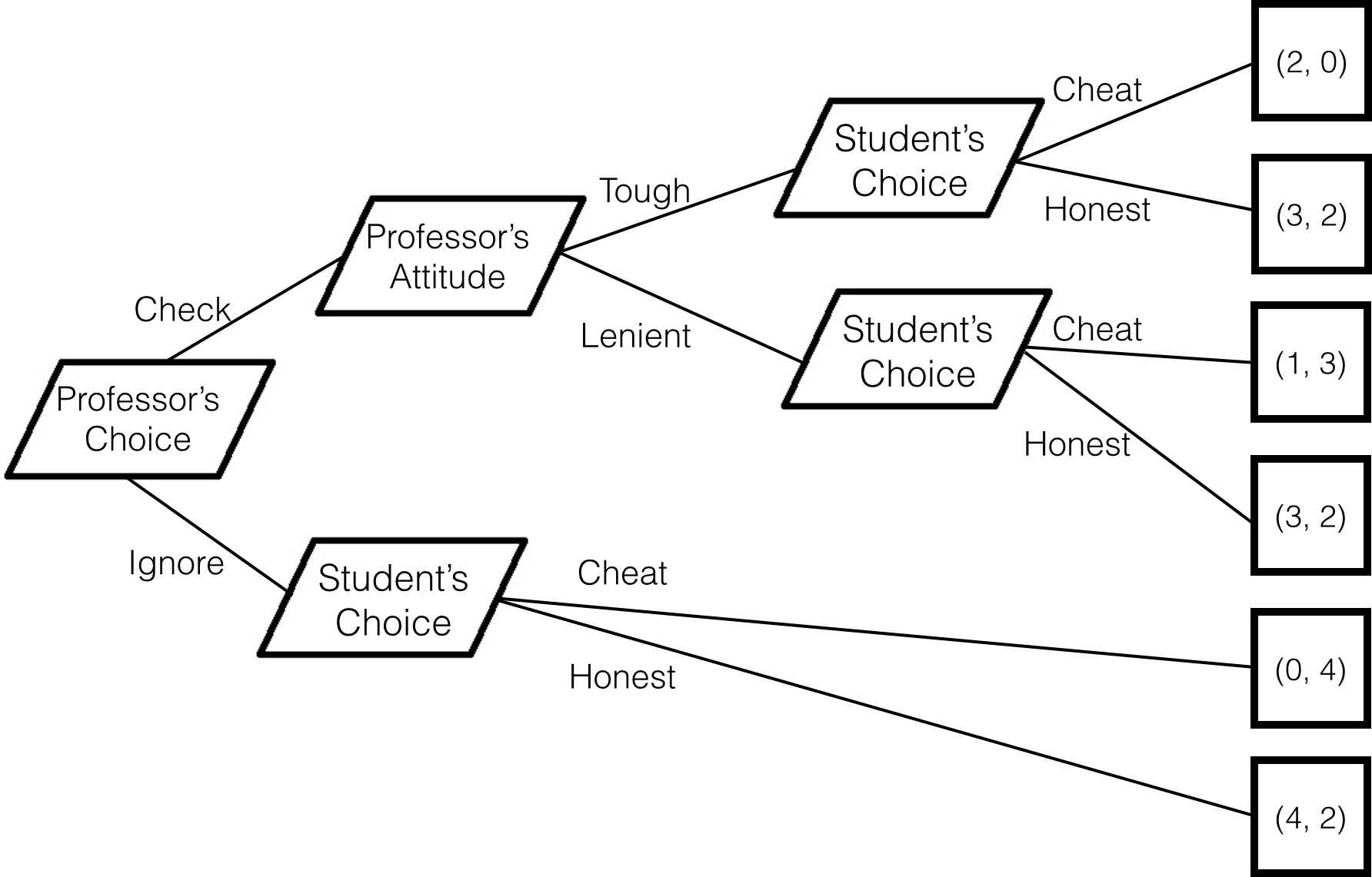
Figure 20.3 Cheating student’s game tree.

Solve this using backwards induction. First, assume the professor checks and is tough. The student can get 2 points for being honest and doing the work and 0 points for cheating, so if she believes the professor’s threat that he is tough is credible, the student will be honest. However, if the student believes the professor will be lenient, cheating will net 3 points to honesty’s 2. On the bottom nodes, if it’s the professor’s policy not to check, then the student’s 4 points for cheating is clearly preferable to the 2 points for being honest, so the professor should assume that the students will cheat.

Removing the dominated positions, the professor’s tree looks like Figure 20.4.

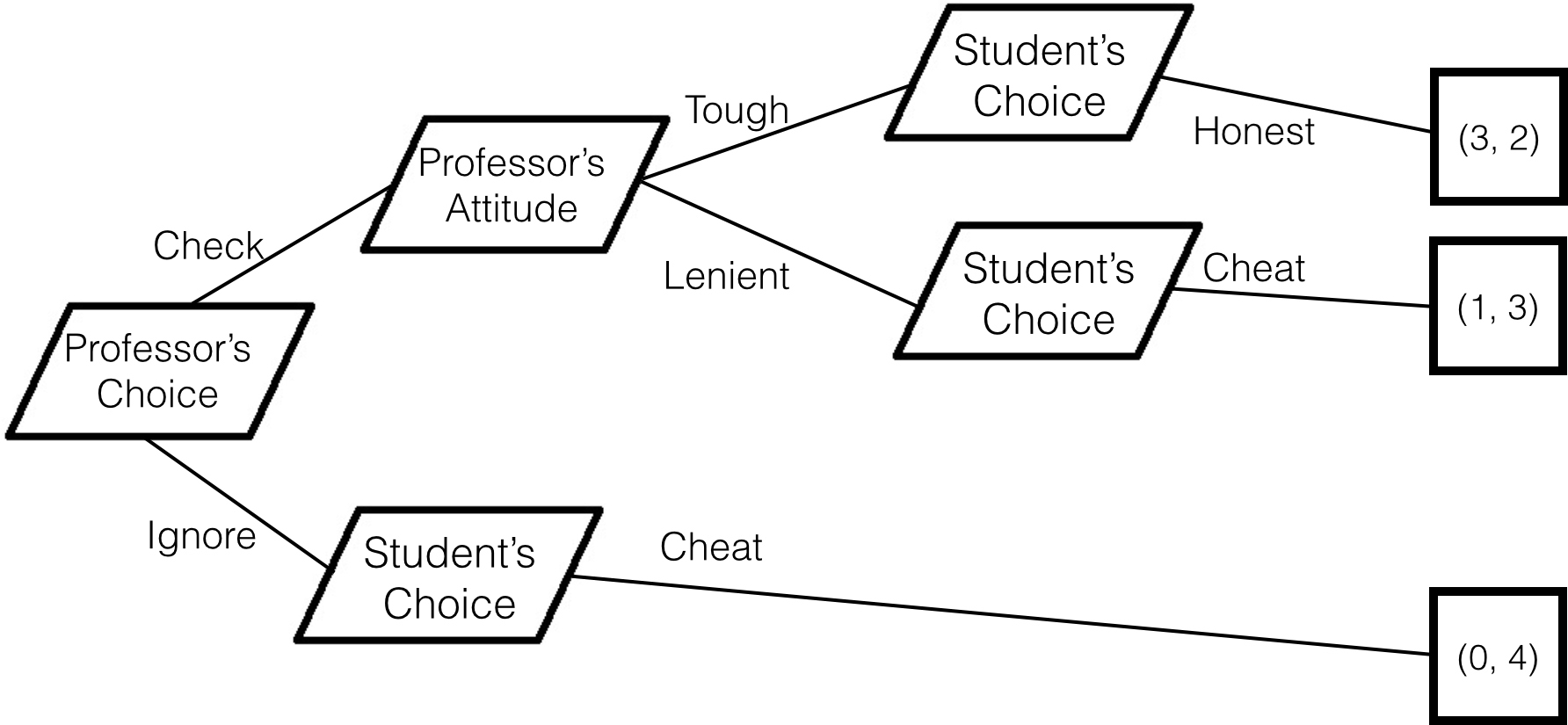
Figure 20.4 Reduced cheating student’s game tree.

Using backwards induction for the professor, given the choice between being tough or being lenient, the professor would prefer the students to work, so he must choose to be tough (3 points to 1 point). Next, he must choose between checking and ignoring. He knows he will receive 3 points from checking because he knows that it will follow that he must be tough and that the students will then work. He knows if he does not check, students will want to cheat and he will receive 0 points.

Thus, professors who value students doing their work must follow through on their commitment to enforcing their threats. Otherwise, the threat of punishment will not be credible and the student will cheat. Equilibrium is the professor checking and being tough while the student is honest. This arrangement is not in the short-term interests of either party: The professor has to spend time checking and prosecuting students and students have to spend more time on their work. (3, 2) is not Pareto optimal. The (4, 2) node of the professor not checking and the students doing their work makes one party better off without reducing the utility of the other party. But because of the commitment issues that causes, it’s not an equilibrium result. If the (4, 2) node were available, students would just choose to cheat for the easy 4 points.

Promises and Commitment Problems

The double-cross has a long history as a narrative hook. In it, two characters come to an agreement on something that cannot happen at the same time. Party A completes his part of the bargain, but then Party B reneges after getting what she wants. Usually this is framed as a character being evil, but you can see how it can be a perfectly rational play of a game.

Imagine two characters, Lando and Vader. Vader gives Lando the choice of giving up his friend Han in order to keep Vader’s forces out of his city. Lando has to make that choice before Vader makes his choice.

Lando’s preferences:

• Free Han and No Occupation

• Han to Empire and No Occupation

• Free Han and Occupation

• Han to Empire and Occupation

Vader’s Preferences:

• Han to Empire and Occupation

• Han to Empire and No Occupation

• Free Han and Occupation

• Free Han and No Occupation

The game tree looks like Figure 20.5.

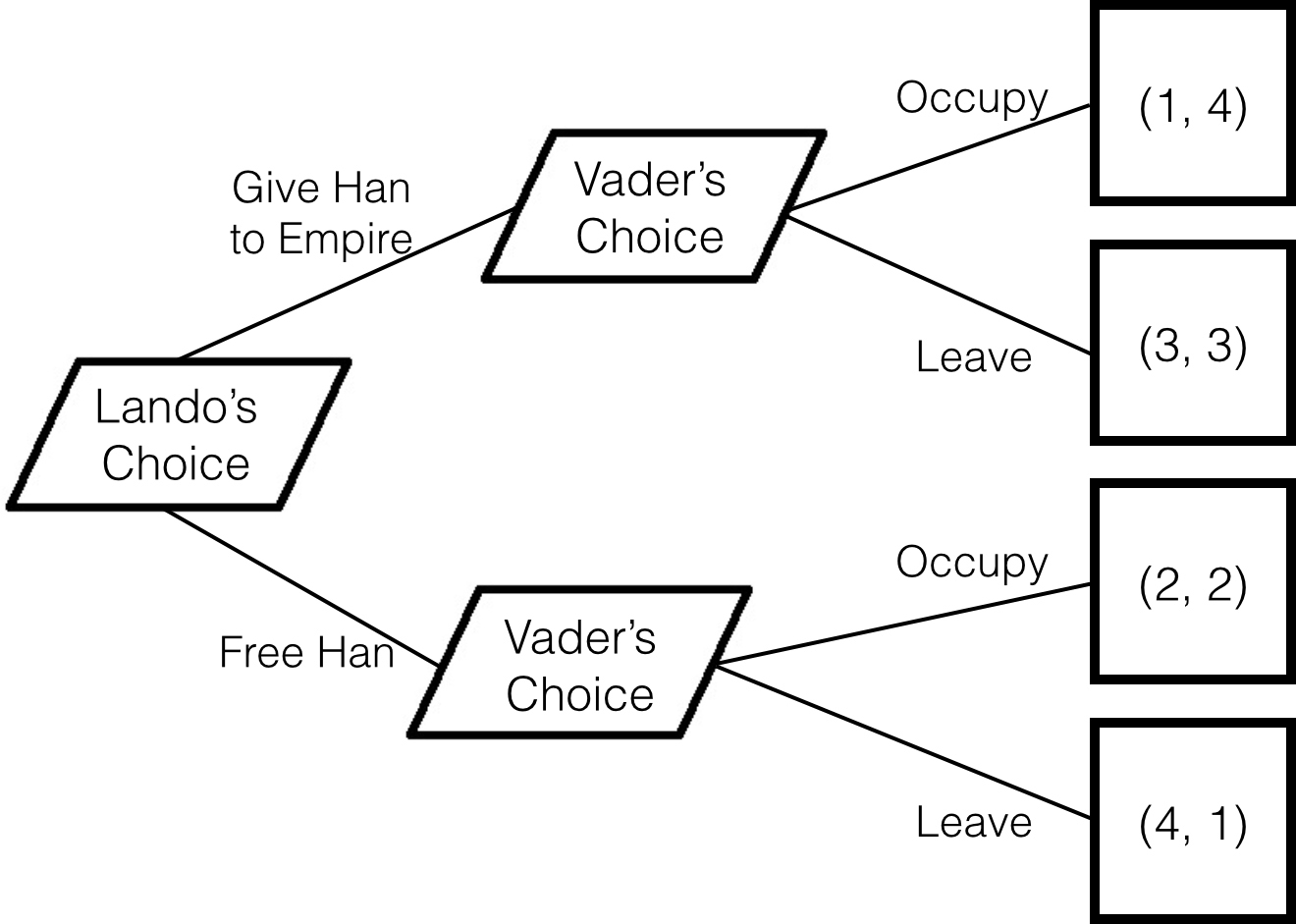
Figure 20.5 Lando/Vader game tree.

Using backwards induction, if Lando gives up Han, it’s better for Vader to occupy (4 versus 3). If Lando does not give up Han, it’s still better for Vader to occupy (2 versus 1). So Lando should know that Vader is going to occupy one way or the other and not choose to give up Han (3 versus 2). In other words, if someone made a feature film in which Lando gives up Han, audiences should not be surprised if Vader still occupies.

With this much benefit from a double-cross, why do we all not use this strategy all the time? Luckily, we have created ways to ensure coordination. Contracts are one mechanism.

Say you are a car dealer and you order a car from the factory. It costs you $20,000 to buy and costs the factory $15,000 to make. When you get ready to sell the car to your customer, you value the car at $25,000. In a normal trade situation, you make the transaction and are $5000 better off and the factory is $5000 better off. But what if the factory could just take your money and run without giving you the car? Then they could net $20,000 instead of $5000. You would know that they could do that, though, and so by backwards induction you would never buy a car in the first place. Neither party would gain or lose anything.

Instead, you sign a contract. If the car is not delivered, you get your $20,000 back. Now the decision tree looks different (Figure 20.6).

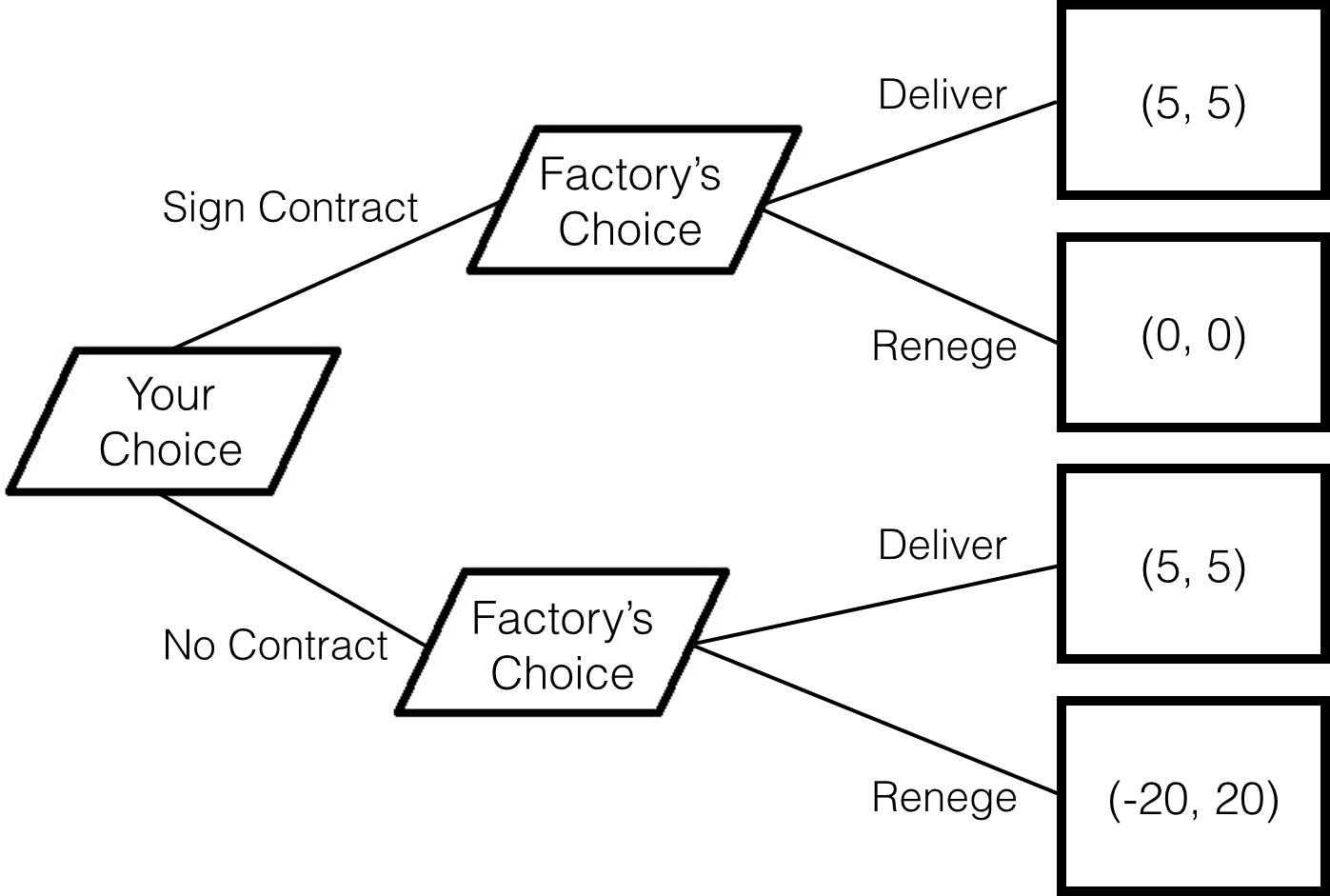
Figure 20.6 The contract game tree with payouts in thousands of dollars.

Here the outcome of the game shifts from the no benefit for either (0, 0) of not having the contract to a (5, 5) equilibrium with the concept of the contract. Both players win.

Iterated Games

The prisoner’s dilemma works because the players make their decisions simultaneously without communicating. But most games can be played over and over again. If a player knows there might be repercussions, should he change his strategy?

What should players do if they have to play the prisoner’s dilemma multiple times? As a reminder, Table 20.1 shows what the payoffs look like.

Table 20.1 Prisoner’s Dilemma

Player A can choose to cooperate or defect. You can represent those strategies with a capital C or capital D, respectively. Player B can do the same, but to differentiate these strategies from those of Player A, use a lowercase c and d. If you want to note the result where both players defect, you can write (Dd). Or if Player A cooperates and Player B defects, you can write (Cd).

It would stand to reason that if you know you will be playing this game over and over again (and that your opponent/partner knows this as well), you will just agree to cooperate forever, ensuring that you both get 2 points per game.

As an example, what happens if these two players play the game for four iterations and try to use this strategy? Theoretically, you can see (Cc) for the first three games. But in the fourth, both players know that this iteration is the last. They have no reason to keep cooperating, especially if they believe the other player will continue cooperating. So in the last game, both defect: (Dd).

Remember, though, that this information is available to both players. If they know that the fourth iteration will end in (Dd), then by the same logic, the last iteration is actually the third iteration. But the same logic that sabotaged the fourth iteration now sabotages the third. Both players see an advantage in defecting, so the result is (Dd). Now the second iteration is the last iteration. But again the same logic applies. This works backward until all games end with (Dd). By induction, any n game of prisoner’s dilemma in which n is known to both players ends in (Dd) on each iteration.

This never-ending betrayal, however, makes no sense when you compare it to how individuals play in the real world.

Experimenting with Strategies

Political scientist Robert Axelrod studied the question of what the best strategy for an iterated prisoner’s dilemma would be by posing a contest.¹ He collected diverse strategies of varying complexity from psychologists, economists, political scientists, and mathematicians and used a computer program to pit them against each other to find out organically which was the best. From this, he hoped to glean principles for ensuring success beyond the one point per game that the equilibrium result predicts.

¹ Axelrod, R. (1984). The Evolution of Cooperation. New York: Basic Books.

Here are some of the entrants:²

² Axelrod, R. (1980). “Effective Choice in the Prisoner’s Dilemma.” Journal of Conflict Resolution, 24(1), 3–25.

• RANDOM: Play randomly. Choose C or D by coin flip every round.

• TIT-FOR-TAT: In the first round, cooperate. In any other round, do what the opponent did in the previous round.

• TIT-FOR-TAT PLUS: In the first round, cooperate. After a defection by the opponent, defect. After a cooperation by the opponent, cooperate with a probability of 9/10.

• GRIM TRIGGER: In the first round, cooperate. If the opponent defects, defect and continue defecting for the rest of the game. Grim Trigger never forgives.

• ESCALATION: In the first round, cooperate. If the opponent defects, defect once in the next round. If the opponent defects again, defect in the next two rounds. Increase defection by one round each time, punishing the opponent more and more for defection.

• GROFMAN: If (Cd) or (cD) happened on the previous round, choose C with a probability of 2/7. Otherwise, choose D.

Axelrod set up the experiment so that each strategy played every other one, in addition to playing against itself. For example, if Tit-for-Tat Plus played against Grim Trigger, it might look something like Table 20.2.

Table 20.2 Tit-for-Tat Plus versus Grim Trigger

In the first rounds, everyone cooperated and did really well, scoring 2 points per round. But eventually, the rule in Tit-for-Tat Plus where 10 percent of the time it chooses to defect after a cooperation caused the player to choose D. Once Grim Trigger saw that, it defected forever and the two became locked into (Dd) for the rest of the iterations, earning only one point per round.

The results at the end of the tournament were surprising. The shortest program (in terms of lines of code) won the entire contest. The winning strategy was Tit-for-Tat: In the first round, cooperate. In any other round, do what the opponent did in the previous round. It destroyed much more complicated strategies. For instance, you might think that Tit-for-Tat Plus would be superior because every once in a while it can eke out a couple of bonus points by defecting when someone thinks it will cooperate. However, against strategies like Grim Trigger that never forgive a defection, this ends up torpedoing the entire game for both players.

Successful Strategies

Axelrod found three strategic concepts that provided the best results in his tournament. First, the strategy had to be nice. This meant that it never defected first. If two nice strategies paired up, they would cooperate forever. Ironically, despite its scary-sounding name, Grim Trigger is a nice strategy. If its opponent never defects, neither does Grim Trigger. The top eight strategies in Axelrod’s tournament were all nice strategies. There was even a large gap in points between the worst nice strategy and the best non-nice strategy.

Next, what differentiated the nice strategies from one another was how they played against those who were not nice. The second concept that Axelrod determined helped the winning strategies was forgiveness. That is, once an opponent defected, he would cooperate again with that same opponent in the future. Grim Trigger is the opposite of a forgiving rule. No matter what, it plays by the maxim “Fool me once, shame on you. Fool me twice, shame on me.” It never forgives. Escalation forgives after one move the first time, two moves the second time, three moves the third time, and so on. Tit-for-Tat, the winner, forgives after only one move no matter what.

Lastly, the strategy had to be non-envious. Strategies that look at the opponent’s success as a measure of the player’s failure lead to poor decisions being made to rectify the inequality. Those strategies can serve to reduce the inequality between players, but they do so by lowering both players’ scores. If the goal is to score the most, then envious strategies are not successful. For the resounding success of Tit-for-Tat in many different tournaments, Axelrod notes a poignant result: Tit-for-Tat never received more points than its opponent. It did better than everyone else on average because its design allowed for both players to succeed, whereas other strategies ended up in long strings of mutual defection. This works because the prisoner’s dilemma is not zero-sum. Both players can succeed.

Axelrod says to be careful in extrapolating that Tit-for-Tat is the optimal solution for an iterated prisoner’s dilemma. It won the matchup only between the strategies submitted. There are others, in retrospect, that would do better, such as a strategy Axelrod called Tit-for-Two-Tats. It’s more forgiving than Tit-for-Tat in that it defects only if the opponent defected in the previous two rounds. Taking this to an extreme, would the most forgiving strategy be one that always cooperated no matter what? By pairing overly forgiving strategies with “not nice” strategies, Axelrod shows that a strategy must be retaliatory to some degree, especially against “not nice” strategies. Being nice and forgiving is a great strategy when you are paired up with others with similar strategies, but it does terribly when paired up with strategies that are meant to exploit.

Axelrod cautions that strategies that attempt to be too clever are likely to fail. Strategies that tried to predict the other player’s move and defect when they cooperated often failed. These inferences were often complicated and ended up playing pseudorandomly. The best strategy against Tit-for-Tat is to simply always cooperate. Yet these predictive strategies that tried to outguess Tit-for-Tat ended up defecting at least once, which decreased both players’ overall score.

What does this mean for game design? Most online multiplayer videogames are set up so that the players play and then never meet again. In these games, the most successful strategies are the mean ones—to always defect. In games with what Axelrod calls “the shadow of the future,” the specter of future games allows players to create strategies that yield better results than what their strategy would yield in a single game by defecting. This has implications for all multiplayer game design. By creating hooks that increase “the shadow of the future,” players can essentially be punished for antisocial or anticompetitive behavior and be rewarded for cooperative and goal-aligned behavior. This happens not because of some mystical sense of community, but because of the same incentives that cause players to act antisocial in the first place.

Summary

• You can use game trees to visualize sequential games as a process of decisions and events that read from left to right.

• Sequential games can be solved for their equilibria by a process called backwards induction.

• Games that are played multiple times in succession may have different player behaviors than games played only once.

• In experiments, strategies that were initially cooperative, provocable to punishment and forgiveness, and not concerned with the opponent’s payoffs performed the best over iterated prisoner’s dilemmas.

• By increasing the “shadow of the future,” you can create an environment in which cooperative behaviors are more likely to endure.