Chapter 9: Review of Probability and Probabilistic Sampling

Overview

Probability Distributions and Density Functions

The Normal and t Distributions

The Usefulness of Theoretical Models

When Samples Surprise Us: Ordinary and Extraordinary Sampling Variability

Case 1: Sample Observations of a Categorical Variable

Case 2: Sample Observations of a Continuous Variable

Conclusion

Overview

The past three chapters have focused on probability—a subject that forms the crucial link between descriptive statistics and statistical inference. From the standpoint of statistical inference, probability theory provides a valuable framework for understanding the variability of probability-based samples. Before moving forward with inference, this short chapter reviews several of the major ideas presented in Chapters 6 through 8, emphasizing two central concepts: (a) probability models are often very useful summaries of empirical phenomena, and (b) sometimes a probability model can provide a framework for deciding if an empirical finding is unexpected. In addition, we will see another JMP script to help visualize probability models. As we did in Chapter 5, we will use the WDI data table to support the discussion.

Probability Distributions and Density Functions

We began the coverage of probability in Chapter 6 with elementary rules concerning categorical events, then moved on to numerical outcomes of random processes. In this chapter, we will start the review by remembering that we can use discrete probability distributions to describe the variability of random outcomes of a discrete random variable. A discrete distribution essentially specifies all possible numerical values for a variable as well as the probability of each distinct value. For example, a rural physician might track the number of patients reporting flu-like symptoms to her each day during flu season. The number of patients will vary from day to day, but the number will be a comparatively small integer.

In some settings, we know that a random process will generate observed values that are described by a formula, such as in the case of a binomial or Poisson process. For example, if we intend to draw a random sample from a large population and count the number of times a single categorical outcome is observed, we can reliably use a distribution to assess the likelihood of each possible outcome. The only requirement is that we know the size of the sample and we know the proportion of the population sharing the categorical outcome. As we will see later, we know that approximately one-third of the countries in the WDI table are classified as “high income” nations. The binomial distribution can predict the likelihood of selecting a random sample of, say, 12 nations and observing a dozen high-income countries.

The Normal and t Distributions

When the variable of interest is continuous, we use a density function to describe its variation. In conventional parlance, a continuous density function is said to specify the distribution of a variable or family of variables. Chapter 7 presented an in-depth treatment of the normal model and some of its uses. The normal model is one notable example of a theoretical continuous distribution, that is, a distribution that can be characterized mathematically. In Chapter 8 we encountered Gosset’s t distribution, similar to the normal in that it is symmetric and mound-shaped. These are two continuous distributions that underlie many of the techniques of inference, and yet there are many more distributions used regularly by statisticians and data analysts.

For a quick visual refresher on the distributions do the following:

1. Help ► Teaching Scripts ► Interactive Teaching Modules ► Distribution Calculator. Figure 9.1 shows the initial view of this distribution calculator.

Figure 9.1: Distribution Calculator

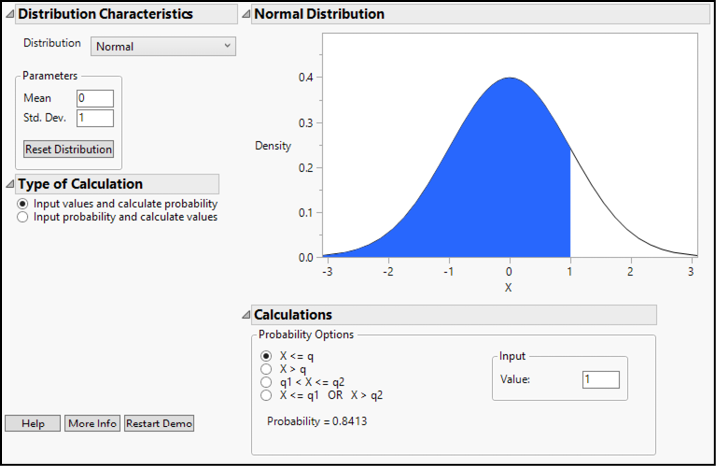
Initially, the calculator displays the standard normal distribution. Remember that all normal distributions are specified by two parameters—a mean and a standard deviation. There are two types of calculations we might want to perform. Either we want to know the probability corresponding to values of the random variable (X), or we want to know the values of X that correspond to specified probabilities. The left side of the dialog box allows the user to enter the parameters and type of calculation.

Below the graph is an input panel to select regions of interest (less than or equal to a value, between two values, and so on) and numerical values either for X or for probability, depending on the type of calculation. Spend a few moments exploring this calculator for normal distributions.

This calculator can perform similar functions for many discrete and continuous distributions, including the few that we have studied. To review and rediscover those distributions, try this:

2. In the upper left of the dialog box, click the button next to Distribution. This opens a drop-down list of all the distributions available for the calculator, as shown in Figure 9.2.

Figure 9.2: Available Distributions

As you scroll through the list, you will find the t, normal, binomial, Poisson, and uniform distributions as well as others that are unfamiliar. Select the familiar ones and notice the parameters of each as well as their characteristic shapes. Curious readers may wish to investigate other distributions in the list as well.

The Usefulness of Theoretical Models

In statistical applications and in introductory statistics courses, we tend to put these theoretical models to work in two ways. In some instances, we might have a model that reliably predicts how random values are generated. For example, we know how to recognize a binomial or Poisson process. We also know when the Central Limit Theorem is relevant. In other instances, we might simply observe that sample data are well-approximated by a known family of distributions (for example, Normal), and we might have sound reasons to accept the risks from using a single formula rather than using a set of data to approximate the population. In such instances, using the model instead of a set of data can be a more efficient way to draw conclusions or make predictions. In the context of statistical inference, we will often use models to approximate sampling distributions. That is, the models will help us characterize the nature of sampling variability and therefore, sampling error.

Let’s consider one illustration of using a model to approximate a population and refer back to Application Scenario 7 of Chapter 7, which in part worked with the cellphone use rates among countries in the WDI data table. We will elaborate on that example here.

1. Open the WDI data table.

2. Select Analyze ►Distribution. Select the column cell (number of mobile cellular subscriptions per 100 people).

Because cell phone usage has changed considerably over the 29-year period, we will focus on just one year, 2017. We can apply a data filter within the Distribution report to accomplish this.

3. Click the red triangle next to Distributions and choose Script ► Local Data Filter to Show and Include only data from the year 2017.

4. Finally, add a normal quantile plot. The comparatively straight diagonal pattern of the points suggests that a normal distribution is an imperfect but reasonable model for this set of 200 observations.

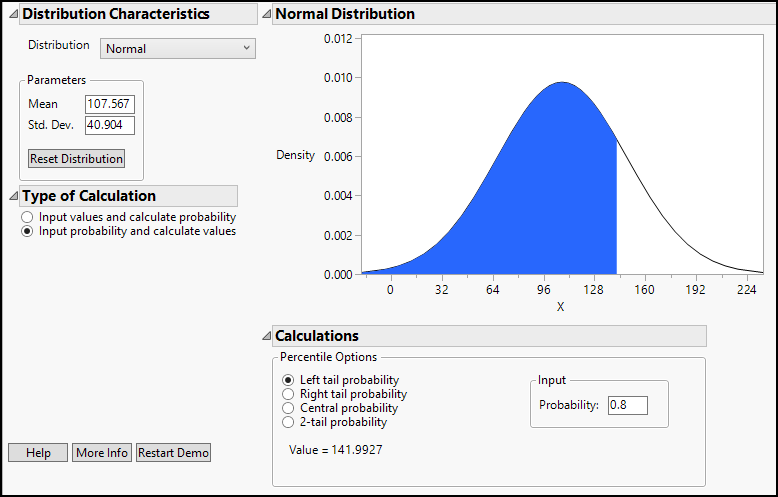
The Distribution command reports selected quantiles for this column. We can see, for example, that 75% of the reporting countries had 129.859 subscriptions or fewer per 100 people. Suppose we wanted to know the approximate value of the 80th percentile. We might use a JMP command to report the 80th percentile from the sample, but we can quickly approximate that value using the normal distribution calculator. From the Distribution report, we know that the sample mean = 107.567 subscriptions, and the sample standard deviation = 40.904 subscriptions.

Follow these steps to calculate the 80th percentile of a theoretical normal population with the same mean and standard deviation.

5. Return to the Distribution and Probability Calculator and re-select Normal distribution in the upper left.

6. In the Parameters panel, enter 107.567 and 40.904 as the mean and standard deviation.

7. Under Type of Calculation, select Input probability and calculate quantiles.

8. Finally, under Calculations, select Left tail probability, and type 0.8 in the Probability box.

The completed dialog box is shown in Figure 9.3. In the lower right panel, we find that the theoretical 80th percentile is 141.99 subscriptions. If you repeat this exercise to locate some of the other percentiles that are reported in the distribution report, you will see that the theoretical normal model is a better approximation for quantiles near the center of the distribution than in the tails.

Figure 9.3: Using a Normal Model to Approximate a Set of Data

When Samples Surprise Us: Ordinary and Extraordinary Sampling Variability

Chapter 8 was devoted to probabilistic sampling and to the idea that samples from a population will inevitably differ from one another. Regardless of the care taken by the investigator, there is an inherent risk that any one sample might poorly represent a parent population or process. Hence, it is important to consider the extent to which samples will tend to vary. The variability of a sample statistic is described by a sampling distribution.

In future chapters, sampling distributions will be crucial underpinnings of the techniques to be covered but will slip into the background. They form the foundation of the analyses, but like the foundations of buildings or bridges, they will be metaphorically underground. We will rely on them, but often we won’t see them or spend much time with them.

As we move forward into statistical inference, we will shift our objective and thought processes away from summarization toward judgment. In inferential analysis, we frequently look at a sample as evidence from a somewhat mysterious population, and we will want to think about the type of population that would have yielded such a sample. As such, we will begin to think about samples that would be typical of a particular population and those that would be unusual, surprising, or implausible.

All samples vary, and the shape, center, and variability depend on whether we are looking at quantitative continuous data or qualitative ordinal or nominal data. Recall that we model the sampling variation differently when dealing with a sample proportion for qualitative, categorical data and the sample mean for continuous data. Let’s consider each case separately.

Case 1: Sample Observations of a Categorical Variable

To illustrate, consider the WDI data table once again. The table contains 42 different columns of data gathered over 29 years. Of the 215 countries, more than one-third are classified as high income (80 of 215 nations = 0.372). If we were to draw a random sample of just twelve observations from the 6,235 rows, we would anticipate that approximately four of the twelve sample observations would be high-income nations. We should also anticipate some variation in that count, though. Some samples might have four high-income countries, but some might have three, or five, or perhaps even six. Is it likely that a single random sample of 12 would not have any high-income countries? Could another sample have 12? Both are certainly possible, but are they plausible outcomes of a truly random process?

The process of selecting 12 nations from a set of 6,235 observations and counting the number of high-income nations is approximately a binomial process. It is only approximately binomial because the probability of success changes very slightly after each successive country is chosen; for the purposes of this discussion, the approximation is sufficient.1 As such, we can use the binomial distribution to describe the likely extent of sampling variation among samples of 12 countries.

1. In the probability calculator, select the Binomial distribution.

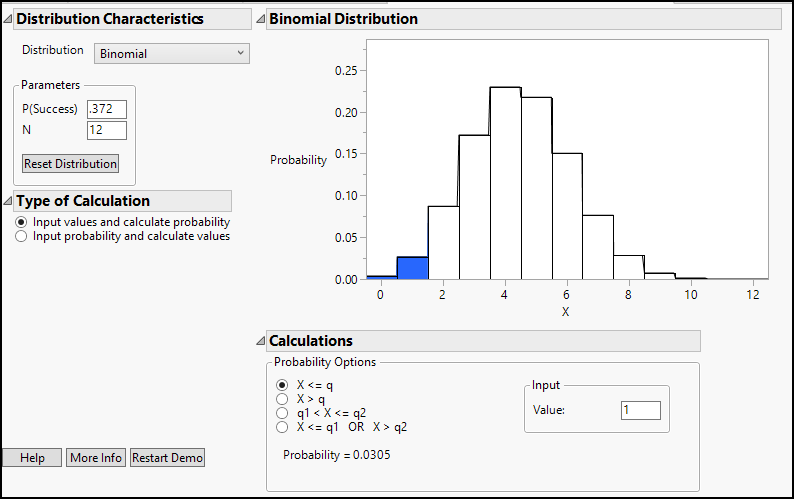
2. Specify that the probability of success is 0.372 and a sample size, N, of 12.

3. Choose Input values and calculate probability.

Your screen will look like Figure 9.4. The binomial histogram (reflecting the discrete number of successes in twelve trials) is initially set to show the probability of obtaining one or fewer high-income countries. This probability is represented by the blue shading, and at the bottom of the dialog box, we find that it is 0.0305. The other Probability Options in the Calculations panel allow us to find probabilities greater than a value, between two values, or in the tails of the distribution.

Figure 9.4: A Binomial Distribution

4. Below the histogram, click the radio button marked X > q, and enter a 6 into the Input panel box Qa.

5. The probability that a 12-country sample will contain more than six high-income countries is 0.1134. Repeat step 3 for seven, eight, and nine countries; notice that the probability becomes vanishingly small.

Such random samples might be logically possible but are so unlikely as to be considered nearly impossible. It is quite likely that this population would generate samples with between, for example, three and six high-income countries, but unlikely to yield a sample with zero or 10 high-income nations.

Case 2: Sample Observations of a Continuous Variable

For this example, we will move away from the WDI data and return to the Airline delays 3 data that we recently investigated in Chapter 8. For this illustration, we will work with the column called DISTANCE, which is the number of miles between the origin and destination airports. As before, we will investigate the variability of sample means to get a better understanding of potential sampling error. Equipped with the knowledge of the true population mean, we want to see how often random samples might have a surprisingly small or large mean.

1. Open the Airline delays 3 data table.

2. Create a distribution report for the column DISTANCE.

This column is right-skewed because no flight can have a negative distance. Many are less than 1,000 miles, but a few are considerably longer.

Usually, we think of samples as coming from a very large population or from an ongoing process. This data table represents 632,075 flights during one month in North America. We can think of commercial air travel as a continuous process. For the sake of this discussion, imagine that this sample is representative of the ongoing process.

If all flights were the same length, then any sample we might draw would provide the same evidence about the process. In fact, a sample of n=1 is sufficient to represent the process. Our challenge arises from the very fact that individual flights vary; because of those individual differences, each sample will be different.

In Chapter 8, we used the Sampling Distribution simulator to simulate thousands of random samples of size n = 200 from the data table. This process is sometimes known as bootstrap sampling or resampling, in which we repeatedly sample and replace values from a single sample until we have generated an empirical sampling distribution.

For this illustration, let’s consider random samples of size 45 flights. Readers who want to repeat the simulation using the DISTANCE column should go back to the section of Chapter 8 entitled “Sampling Distribution of the Sample Mean,” and regenerate perhaps 10,000 iterations until the histogram is relatively smooth and mound-shaped. Be forewarned that this can take a long time. Bootstrapping from such a large data table can consume computing resources. The results of one such simulation appear in Figure 9.5. The histogram has been revised to more clearly show the horizontal axis. The blue vertical line at 807.3 miles marks the mean of all flights.

Figure 9.5: A Bootstrap Sampling Distribution

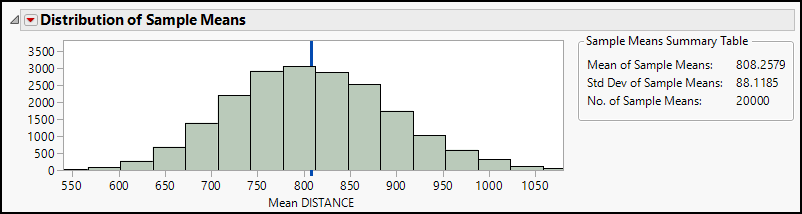
So what message are we supposed to take away from this graph and the resampling exercise? Consider these messages for a start:

● Different 45-observation samples from a given population have different sample means.

● Though different, sample means tend to be “near” the mean of the population.

● We can model the shape, center, and variability of possible sample means.

● Even though DISTANCE in the original sample is very strongly skewed to the right, repeated samples consistently generate sample means that vary symmetrically—with an approximately normal distribution predicted by the Central Limit Theorem. Specifically, the CLT says that the sampling distribution will approach ~N(807.3, 87.8).

Very importantly, the histogram establishes a framework for judging the rarity of specific sample mean values. Approximately two-thirds of all possible samples of 45 flights commonly have mean distances between approximately 720 and 900 miles. Sample means will very rarely be smaller than 630 miles or longer than 980 miles. It would be stunning to take a sample of 45 incidents and find a sample mean less than 600 miles.

We cannot conclude that a result is surprising or rare or implausible without first having a clear sense of what is typical. Sampling distributions tell us what is surprising and what is not.

Conclusion

Probability is an interesting and important subject in its own right. For the practice of data analysis, it provides the foundation for the interpretation of data gathered by random sampling methods. This chapter has reviewed the content of three earlier chapters that introduced readers to a few essential elements of probability theory. Taken together, these chapters form the bridge between the two statistical realms of description and inference.