One very popular question to ask about univariate data is What is the typical value? or What's the value around which the data are centered?. To answer these questions, we have to measure the central tendency of a set of data.

We've seen one measure of central tendency already: the mode. The mtcars$carburetors data subset was bimodal, with a two and four carburetor setup being the most popular. The mode is the central tendency measure that is applicable to categorical data.

The mode of a discretized continuous distribution is usually considered to be the interval that contains the highest frequency of data points. This makes it dependent on the method and parameters of the binning. Finding the mode of data from a non-discretized continuous distribution is a more complicated procedure, which we'll see later.

Perhaps the most famous and commonly used measure of central tendency is the mean. The mean is the sum of a set of numerics divided by the number of elements in that set. This simple concept can also be expressed as a complex-looking equation:

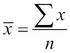
Where (pronounced x bar) is the mean, is the summation of the elements in the data set, and n is the number of elements in the set. (As an aside, if you are intimidated by the equations in this book, don't be! None of them are beyond your grasp—just think of them as sentences of a language you're not proficient in yet.)

The mean is represented as when we are talking about the mean of a sample (or subset) of a larger population, and µ when we are talking about the mean of the population. A population may have too many items to compute the mean directly. When this is the case, we rely on statistics applied to a sample of the population to estimate its parameters.

Another way to express the preceding equation using R constructs is as follows:

  > sum(nums)/length(nums)    # nums would be a vector of numerics

As you might imagine, though, the mean has an eponymous R function that is built-in already:

  > mean(c(1,2,3,4,5))
  [1] 3

The mean is not defined for categorical data; remember that mode is the only measure of central tendency that we can use with categorical data.

The mean—occasionally referred to as the arithmetic mean to contrast with the far less often used geometric, harmonic, and trimmed means—while extraordinarily popular is not a very robust statistic. This is because the statistic is unduly affected by outliers (atypically distant data points or observations). A paradigmatic example where the robustness of the mean fails is its application to the different distributions of income.

Imagine the wages of employees in a company called Marx & Engels, Attorneys at Law, where the typical worker makes $40,000 a year while the CEO makes $500,000 a year. If we compute the mean of the salaries based on a sample of ten that contains just the exploited class, we will have a fairly accurate representation of the average salary of a worker at that company. If however, by the luck of the draw, our sample contains the CEO, the mean of the salaries will skyrocket to a value that is no longer representative or very informative.

More specifically, robust statistics are statistical measures that work well when thrown at a wide variety of different distributions. The mean works well with one particular type of distribution, the normal distribution, and, to varying degrees, fails to accurately represent the central tendency of other distributions.

Figure 2.3: A normal distribution

The normal distribution (also called the Gaussian distribution if you want to impress people) is frequently referred to as the bell curve because of its shape. As seen in the preceding image, the vast majority of the data points lie within a narrow band around the center of the distribution—which is the mean. As you get further and further from the mean, the observations become less and less frequent. It is a symmetric distribution, meaning that the side that is to the right of the mean is a mirror image of the left side of the mean.

Not only is the usage of the normal distribution extremely common in statistics, but it is also ubiquitous in real life, where it can model anything from people's heights to test scores; a few will fare lower than average, and a few fare higher than average, but most are around average.

The utility of the mean as a measure of central tendency becomes strained as the normal distribution becomes more and more skewed, or asymmetrical.

If the majority of the data points fall on the left side of the distribution, with the right side tapering off slower than the left, the distribution is considered positively skewed or right-tailed. If the longer tail is on the left side and the bulk of the distribution is hanging out to the right, it is called negatively skewed or left-tailed. This can be seen clearly in the following images:

Figure 2.4a: A negatively skewed distribution

Figure 2.4b: A positively skewed distribution

Luckily, for cases of skewed distributions, or other distributions for which the mean is inadequate to describe, we can use the median instead.

The median of a dataset is the middle number in the set after it is sorted. Less concretely, it is the value that cleanly separates the higher-valued half of the data and the lower-valued half.

The median of the set of numbers {1, 3, 5, 6, 7} is 5. In the set of numbers with an even number of elements, the mean of the two middle values is taken to be the median. For example, the median of the set {3, 3, 6, 7, 7, 10} is 6.5. The median is the 50th percentile, meaning that 50 percent of the observations fall below that value.

  > median(c(3, 7, 6, 10, 3, 7))
  [1] 6.5

Consider the example of Marx & Engels, Attorneys at Law that we referred to earlier. Remember that if the sample of employees' salaries included the CEO, it would give our mean a non-representative value. The median solves our problem beautifully. Let's say our sample of 10 employees' salaries was {41000, 40300, 38000, 500000, 41500, 37000, 39600, 42000, 39900, 39500}. Given this set, the mean salary is $85,880 but the median is $40,100—way more in line with the salary expectations of the proletariat at the law firm.

In symmetric data, the mean and median are often very close to each other in value, if not identical. In asymmetric data, this is not the case. It is telling when the median and the mean are very discrepant. In general, if the median is less than the mean, the data set has a large right tail or outliers/anomalies/erroneous data to the right of the distribution. If the mean is less than the median, it tells the opposite story. The degree of difference between the mean and the median is often an indication of the degree of skewness.

This property of the median—resistance to the influence of outliers—makes it a robust statistic. In fact, the median is the most outlier-resistant metric in statistics.

As great as the median is, it's far from being perfect to describe data just by its own. To see what I mean, check out the three distributions in the following image. All three have the same mean and median, yet all three are very different distributions.

Clearly, we need to look to other statistical measures to describe these differences.

Figure 2.5: three distributions with the same mean and median