Winemaking is a challenging and competitive business that offers the potential for great profit. However, there are numerous factors that contribute to the profitability of a winery. As an agricultural product, variables as diverse as the weather and the growing environment impact the quality of a varietal. The bottling and manufacturing can also affect the flavor for better or worse. Even the way the product is marketed, from the bottle design to the price point, can affect the customer's perception of taste.
As a consequence, the winemaking industry has heavily invested in data collection and machine learning methods that may assist with the decision science of winemaking. For example, machine learning has been used to discover key differences in the chemical composition of wines from different regions, or to identify the chemical factors that lead a wine to taste sweeter.
More recently, machine learning has been employed to assist with rating the quality of wine—a notoriously difficult task. A review written by a renowned wine critic often determines whether the product ends up on the top or bottom shelf, in spite of the fact that even the expert judges are inconsistent when rating a wine in a blinded test.
In this case study, we will use regression trees and model trees to create a system capable of mimicking expert ratings of wine. Because trees result in a model that is readily understood, this can allow the winemakers to identify the key factors that contribute to better-rated wines. Perhaps more importantly, the system does not suffer from the human elements of tasting, such as the rater's mood or palate fatigue. Computer-aided wine testing may therefore result in a better product as well as more objective, consistent, and fair ratings.
To develop the wine rating model, we will use data donated to the UCI Machine Learning Data Repository (http://archive.ics.uci.edu/ml) by P. Cortez, A. Cerdeira, F. Almeida, T. Matos, and J. Reis. The data include examples of red and white Vinho Verde wines from Portugal—one of the world's leading wine-producing countries. Because the factors that contribute to a highly rated wine may differ between the red and white varieties, for this analysis we will examine only the more popular white wines.
The white wine data includes information on 11 chemical properties of 4,898 wine samples. For each wine, a laboratory analysis measured characteristics such as acidity, sugar content, chlorides, sulfur, alcohol, pH, and density. The samples were then rated in a blind tasting by panels of no less than three judges on a quality scale ranging from zero (very bad) to 10 (excellent). In the case of judges disagreeing on the rating, the median value was used.
The study by Cortez evaluated the ability of three machine learning approaches to model the wine data: multiple regression, artificial neural networks, and support vector machines. We covered multiple regression earlier in this chapter, and we will learn about neural networks and support vector machines in Chapter 7, Black Box Methods – Neural Networks and Support Vector Machines. The study found that the support vector machine offered significantly better results than the linear regression model. However, unlike regression, the support vector machine model is difficult to interpret. Using regression trees and model trees, we may be able to improve the regression results while still having a model that is easy to understand.
As usual, we will use the read.csv() function to load the data into R. Since all of the features are numeric, we can safely ignore the stringsAsFactors parameter:
> wine <- read.csv("whitewines.csv")
The wine data includes 11 features and the quality outcome, as follows:
> str(wine) 'data.frame': 4898 obs. of 12 variables: $ fixed.acidity : num 6.7 5.7 5.9 5.3 6.4 7 7.9 ... $ volatile.acidity : num 0.62 0.22 0.19 0.47 0.29 0.12 ... $ citric.acid : num 0.24 0.2 0.26 0.1 0.21 0.41 ... $ residual.sugar : num 1.1 16 7.4 1.3 9.65 0.9 ... $ chlorides : num 0.039 0.044 0.034 0.036 0.041 ... $ free.sulfur.dioxide : num 6 41 33 11 36 22 33 17 34 40 ... $ total.sulfur.dioxide: num 62 113 123 74 119 95 152 ... $ density : num 0.993 0.999 0.995 0.991 0.993 ... $ pH : num 3.41 3.22 3.49 3.48 2.99 3.25 ... $ sulphates : num 0.32 0.46 0.42 0.54 0.34 0.43 ... $ alcohol : num 10.4 8.9 10.1 11.2 10.9 ... $ quality : int 5 6 6 4 6 6 6 6 6 7 ...
Compared with other types of machine learning models, one of the advantages of trees is that they can handle many types of data without preprocessing. This means we do not need to normalize or standardize the features.
However, a bit of effort to examine the distribution of the outcome variable is needed to inform our evaluation of the model's performance. For instance, suppose that there was a very little variation in quality from wine-to-wine, or that wines fell into a bimodal distribution: either very good or very bad. To check for such extremes, we can examine the distribution of quality using a histogram:
> hist(wine$quality)
This produces the following figure:

The wine quality values appear to follow a fairly normal, bell-shaped distribution, centered around a value of six. This makes sense intuitively because most wines are of average quality; few are particularly bad or good. Although the results are not shown here, it is also useful to examine the summary(wine) output for outliers or other potential data problems. Even though trees are fairly robust with messy data, it is always prudent to check for severe problems. For now, we'll assume that the data is reliable.
Our last step then is to divide into training and testing datasets. Since the wine data set was already sorted into random order, we can partition into two sets of contiguous rows as follows:
> wine_train <- wine[1:3750, ] > wine_test <- wine[3751:4898, ]
In order to mirror the conditions used by Cortez, we used sets of 75 percent and 25 percent for training and testing, respectively. We'll evaluate the performance of our tree-based models on the testing data to see if we can obtain results comparable to the prior research study.
We will begin by training a regression tree model. Although almost any implementation of decision trees can be used to perform regression tree modeling, the rpart (recursive partitioning) package offers the most faithful implementation of regression trees as they were described by the CART team. As the classic R implementation of CART, the rpart package is also well-documented and supported with functions for visualizing and evaluating the rpart models.
Install the rpart package using the install.packages("rpart") command. It can then be loaded into your R session using the library(rpart) command. The following syntax will train a tree using the default settings, which typically work fairly well. If you need more finely-tuned settings, refer to the documentation for the control parameters using the ?rpart.control command.

Using the R formula interface, we can specify quality as the outcome variable and use the dot notation to allow all the other columns in the wine_train data frame to be used as predictors. The resulting regression tree model object is named m.rpart to distinguish it from the model tree that we will train later:
> m.rpart <- rpart(quality ~ ., data = wine_train)
For basic information about the tree, simply type the name of the model object:
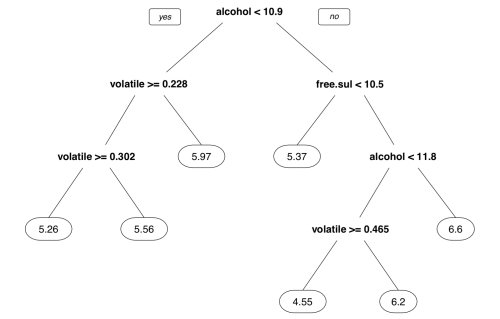
> m.rpart n= 3750 node), split, n, deviance, yval * denotes terminal node 1) root 3750 2945.53200 5.870933 2) alcohol< 10.85 2372 1418.86100 5.604975 4) volatile.acidity>=0.2275 1611 821.30730 5.432030 8) volatile.acidity>=0.3025 688 278.97670 5.255814 * 9) volatile.acidity< 0.3025 923 505.04230 5.563380 * 5) volatile.acidity< 0.2275 761 447.36400 5.971091 * 3) alcohol>=10.85 1378 1070.08200 6.328737 6) free.sulfur.dioxide< 10.5 84 95.55952 5.369048 * 7) free.sulfur.dioxide>=10.5 1294 892.13600 6.391036 14) alcohol< 11.76667 629 430.11130 6.173291 28) volatile.acidity>=0.465 11 10.72727 4.545455 * 29) volatile.acidity< 0.465 618 389.71680 6.202265 * 15) alcohol>=11.76667 665 403.99400 6.596992 *
For each node in the tree, the number of examples reaching the decision point is listed. For instance, all 3,750 examples begin at the root node, of which 2,372 have alcohol < 10.85 and 1,378 have alcohol >= 10.85. Because alcohol was used first in the tree, it is the single most important predictor of wine quality.
Nodes indicated by * are terminal or leaf nodes, which means that they result in a prediction (listed here as yval). For example, node 5 has a yval of 5.971091. When the tree is used for predictions, any wine samples with alcohol < 10.85 and volatile.acidity < 0.2275 would therefore be predicted to have a quality value of 5.97.
A more detailed summary of the tree's fit, including the mean squared error for each of the nodes and an overall measure of feature importance, can be obtained using the summary(m.rpart) command.
Although the tree can be understood using only the preceding output, it is often more readily understood using visualization. The rpart.plot package by Stephen Milborrow provides an easy-to-use function that produces publication-quality decision trees.
Note
For more information on rpart.plot, including additional examples of the types of decision tree diagrams that the function can produce, refer to the author's website at http://www.milbo.org/rpart-plot/.
After installing the package using the install.packages("rpart.plot") command, the rpart.plot() function produces a tree diagram from any rpart model object. The following commands plot the regression tree we built earlier:
> library(rpart.plot) > rpart.plot(m.rpart, digits = 3)
The resulting tree diagram is as follows:
In addition to the digits parameter that controls the number of numeric digits to include in the diagram, many other aspects of the visualization can be adjusted. The following command shows just a few of the useful options: The fallen.leaves parameter forces the leaf nodes to be aligned at the bottom of the plot, while the type and extra parameters affect the way the decisions and nodes are labeled:
> rpart.plot(m.rpart, digits = 4, fallen.leaves = TRUE, type = 3, extra = 101)
The result of these changes is a very different looking tree diagram:

Visualizations like these may assist with the dissemination of regression tree results, as they are readily understood even without a mathematics background. In both cases, the numbers shown in the leaf nodes are the predicted values for the examples reaching that node. Showing the diagram to the wine producers may thus help to identify the key factors that predict the higher rated wines.
To use the regression tree model to make predictions on the test data, we use the predict() function. By default, this returns the estimated numeric value for the outcome variable, which we'll save in a vector named p.rpart:
> p.rpart <- predict(m.rpart, wine_test)
A quick look at the summary statistics of our predictions suggests a potential problem; the predictions fall on a much narrower range than the true values:
> summary(p.rpart) Min. 1st Qu. Median Mean 3rd Qu. Max. 4.545 5.563 5.971 5.893 6.202 6.597 > summary(wine_test$quality) Min. 1st Qu. Median Mean 3rd Qu. Max. 3.000 5.000 6.000 5.901 6.000 9.000
This finding suggests that the model is not correctly identifying the extreme cases, in particular the best and worst wines. On the other hand, between the first and third quartile, we may be doing well.
The correlation between the predicted and actual quality values provides a simple way to gauge the model's performance. Recall that the cor() function can be used to measure the relationship between two equal-length vectors. We'll use this to compare how well the predicted values correspond to the true values:
> cor(p.rpart, wine_test$quality) [1] 0.5369525
A correlation of 0.54 is certainly acceptable. However, the correlation only measures how strongly the predictions are related to the true value; it is not a measure of how far off the predictions were from the true values.
Another way to think about the model's performance is to consider how far, on average, its prediction was from the true value. This measurement is called the mean absolute error (MAE). The equation for MAE is as follows, where n indicates the number of predictions and ei indicates the error for prediction i:

As the name implies, this equation takes the mean of the absolute value of the errors. Since the error is just the difference between the predicted and actual values, we can create a simple MAE() function as follows:
> MAE <- function(actual, predicted) { mean(abs(actual - predicted)) }
The MAE for our predictions is then:
> MAE(p.rpart, wine_test$quality) [1] 0.5872652
This implies that, on average, the difference between our model's predictions and the true quality score was about 0.59. On a quality scale from zero to 10, this seems to suggest that our model is doing fairly well.
On the other hand, recall that most wines were neither very good nor very bad; the typical quality score was around five to six. Therefore, a classifier that did nothing but predict the mean value may still do fairly well according to this metric.
The mean quality rating in the training data is as follows:
> mean(wine_train$quality) [1] 5.870933
If we predicted the value 5.87 for every wine sample, we would have a mean absolute error of only about 0.67:
> MAE(5.87, wine_test$quality) [1] 0.6722474
Our regression tree (MAE = 0.59) comes closer on average to the true quality score than the imputed mean (MAE = 0.67), but not by much. In comparison, Cortez reported an MAE of 0.58 for the neural network model and an MAE of 0.45 for the support vector machine. This suggests that there is room for improvement.
To improve the performance of our learner, let's try to build a model tree. Recall that a model tree improves on regression trees by replacing the leaf nodes with regression models. This often results in more accurate results than regression trees, which use only a single value for prediction at the leaf nodes.
The current state-of-the-art in model trees is the M5' algorithm (M5-prime) by Y. Wang and I.H. Witten, which is a variant of the original M5 model tree algorithm proposed by J.R. Quinlan in 1992.
The M5 algorithm is available in R via the RWeka package and the M5P() function. The syntax of this function is shown in the following table. Be sure to install the RWeka package if you haven't already. Because of its dependence on Java, the installation instructions are included in Chapter 1, Introducing Machine Learning.

We'll fit the model tree using essentially the same syntax as we used for the regression tree:
> library(RWeka) > m.m5p <- M5P(quality ~ ., data = wine_train)
The tree itself can be examined by typing its name. In this case, the tree is very large and only the first few lines of output are shown:
> m.m5p M5 pruned model tree: (using smoothed linear models) alcohol <= 10.85 : | volatile.acidity <= 0.238 : | | fixed.acidity <= 6.85 : LM1 (406/66.024%) | | fixed.acidity > 6.85 : | | | free.sulfur.dioxide <= 24.5 : LM2 (113/87.697%)
You will note that the splits are very similar to the regression tree that we built earlier. Alcohol is the most important variable, followed by volatile acidity and free sulfur dioxide. A key difference, however, is that the nodes terminate not in a numeric prediction, but a linear model (shown here as LM1 and LM2).
The linear models themselves are shown later in the output. For instance, the model for LM1 is shown in the forthcoming output. The values can be interpreted exactly the same as the multiple regression models we built earlier in this chapter. Each number is the net effect of the associated feature on the predicted wine quality. The coefficient of 0.266 for fixed acidity implies that for an increase of 1 unit of acidity, the wine quality is expected to increase by 0.266:
LM num: 1 quality = 0.266 * fixed.acidity - 2.3082 * volatile.acidity - 0.012 * citric.acid + 0.0421 * residual.sugar + 0.1126 * chlorides + 0 * free.sulfur.dioxide - 0.0015 * total.sulfur.dioxide - 109.8813 * density + 0.035 * pH + 1.4122 * sulphates - 0.0046 * alcohol + 113.1021
It is important to note that the effects estimated by LM1 apply only to wine samples reaching this node; a total of 36 linear models were built in this model tree, each with different estimates of the impact of fixed acidity and the other 10 features.
For statistics on how well the model fits the training data, the summary() function can be applied to the M5P model. However, note that since these statistics are based on the training data, they should be used only as a rough diagnostic:
> summary(m.m5p) === Summary === Correlation coefficient 0.6666 Mean absolute error 0.5151 Root mean squared error 0.6614 Relative absolute error 76.4921 % Root relative squared error 74.6259 % Total Number of Instances 3750
Instead, we'll look at how well the model performs on the unseen test data. The predict() function gets us a vector of predicted values:
> p.m5p <- predict(m.m5p, wine_test)
The model tree appears to be predicting a wider range of values than the regression tree:
> summary(p.m5p) Min. 1st Qu. Median Mean 3rd Qu. Max. 4.389 5.430 5.863 5.874 6.305 7.437
The correlation also seems to be substantially higher:
> cor(p.m5p, wine_test$quality) [1] 0.6272973
Furthermore, the model has slightly reduced the mean absolute error:
> MAE(wine_test$quality, p.m5p) [1] 0.5463023
Although we did not improve a great deal beyond the regression tree, we surpassed the performance of the neural network model published by Cortez, and we are getting closer to the published mean absolute error value of 0.45 for the support vector machine model, all by using a much simpler learning method.
Tip
Not surprisingly, we have confirmed that predicting the quality of wines is a difficult problem; wine tasting, after all, is inherently subjective. If you would like additional practice, you may try revisiting this problem after reading Chapter 11, Improving Model Performance, which covers additional techniques that may lead to better results.

