You're at a train terminal looking for the right line to stand in to get on the train from Upstate NY to Penn Station in NYC. You've settled into what you think is the right line, but you're still not sure because it's so crowded and chaotic. Not wanting to wait in the wrong line, you turn to the person closest to you and ask them where they're going: "Penn Station," says the stranger, blithely.

You decide to get some second opinions. You turn to the second closest person and the third closest person and ask them separately: Penn Station and Nova Scotia respectively. The general consensus seems to be that you're in the right line, and that's good enough for you.

If you've understood the preceding interaction, you already understand the idea behind k-Nearest Neighbors (k-NN hereafter) on a fundamental level. In particular, you've just performed k-NN, where k=3. Had you just stopped at the first person, you would have performed k-NN, where k=1.

So, k-NN is a classification technique that, for each data point we want to classify, finds the k closest training data points and returns the consensus. In traditional settings, the most common distance metric is Euclidean distance (which, in two dimensions, is equal to the distance from point a to point b given by the Pythagorean Theorem). Another common distance metric is Manhattan distance, which, in two dimensions, is equal to the sum of the length of the legs of the triangle connecting two data points.

Figure 9.1: Two points on a Cartesian plane. Their Euclidean distance is 5. Their Manhattan distance is 3+4=7

k-Nearest Neighbors is a bit of an oddball technique; most statistical learning methods attempt to impose a particular model on the data and estimate the parameters of that model. Put another way, the goal of most learning methods is to learn an objective function that maps inputs to outputs. Once the objective function is learned, there is no longer a need for the training set.

In contrast, k-NN learns no such objective function. Rather, it lets the data speak for themselves. Since there is no actual learning, per se, going on, k-NN needs to hold on to training dataset for future classifications. This also means that the training step is instantaneous, since there is no training to be done. Most of the time spent during the classification of a data point is spent finding its nearest neighbors. This property of k-NN makes it a lazy learning algorithm.

Since no particular model is imposed on the training data, k-NN is one of the most flexible and accurate classification learners there are, and it is very widely used. With great flexibility, though, comes great responsibility—it is our responsibility that we ensure that k-NN hasn't overfit the training data.

Figure 9.2: The species classification regions of the iris data set using 1-NN

In Figure 9.2, we use the built-in iris dataset. This dataset contains four continuous measurements of iris flowers and maps each observation to one of three species: iris setosa (the square points), iris virginica (the circular points), and iris versicolor (the triangular points). In this example, we use only two of the available four attributes in our classification for ease of visualization: sepal width and petal width. As you can see, each species seems to occupy its own little space in our 2-D feature space. However, there seems to be a little overlap between the versicolor and virginica data points. Because this classifier is using only one nearest neighbor, there appear to be small regions of training data-specific idiosyncratic classification behavior where virginicas is encroaching the versicolor classification region. This is what it looks like when our k-NN overfits the data. In our train station metaphor, this is tantamount to asking only one neighbor what line you're on and the misinformed (or malevolent) neighbor telling you the wrong answer.

k-NN classifiers that have overfit have traded low variance for low bias. It is common for overfit k-NN classifiers to have a 0% misclassification rate on the training data, but small changes in the training data harshly change the classification regions (high variance). Like with regression (and the rest of the classifiers we'll be learning about in this chapter), we aim to find the optimal point in the bias-variance tradeoff—the one that minimizes error in an independent testing set, and not one that minimizes training set misclassification error.

We do this by modifying the k in k-NN and using the consensus of more neighbors. Beware - if you ask too many neighbors, you start to take the answers of rather distant neighbors seriously, and this can also adversely affect accuracy. Finding the "sweet spot", where k is neither too small or two large, is called hyperparameter optimization (because k is called a hyperparameter of k-NN).

Figure 9.3: The species classification regions of the iris data set using 15-NN. The boundaries between the classification regions are now smoother and less overfit

Compare Figure 9.2 to Figure 9.3, which depicts the classification regions of the iris classification task using 15 nearest neighbors. The aberrant virginicas are no longer carving out their own territory in versicolor's region, and the boundaries between the classification regions (also called decision boundaries) are now smoother—often a trait of classifiers that have found the sweet spot in the bias-variance tradeoff. One could imagine that new training data will no longer have such a drastic effect on the decision boundaries—at least not as much as with the 1-NN classifier.

Using k-NN in R

The dataset we will be using for all the examples in this chapter is the PimaIndiansDiabetes dataset from the mlbench package. This dataset is part of the data collected from one of the numerous diabetes studies on the Pima Indians, a group of indigenous Americans who have among the highest prevalence of Type II diabetes in the world—probably due to a combination of genetic factors and their relatively recent introduction to a heavily processed Western diet. For 768 observations, it has nine attributes, including skin fold thickness, BMI, and so on, and a binary variable representing whether the patient had diabetes. We will be using the eight predictor variables to train a classifier to predict whether a patient has diabetes or not.

This dataset was chosen because it has many observations available, has a goodly amount of predictor variables available, and it is an interesting problem. Additionally, it is not unlike many other medical datasets that have a few predictors and a binary class outcome (for example, alive/dead, pregnant/not-pregnant, benign/malignant). Finally, unlike many classification datasets, this one has a good mixture of both class outcomes; this contains 35% diabetes positive observations. Grievously imbalanced datasets can cause a problem with some classifiers and impair our accuracy estimates.

To get this dataset, we are going to run the following commands to install the necessary package, load the data, and give the dataset a new name that is faster to type:

  > # "class" is one of the packages that implement k-NN
  > # "chemometrics" contains a function we need
  > # "mlbench" holds the data set
  > install.packages(c("class", "mlbench", "chemometrics"))
  > library(class)
  > library(mlbench)
  > data(PimaIndiansDiabetes)
  > PID <- PimaIndiansDiabetes

Now, let's divide our dataset into a training set and a testing set using an 80/20 split.

  > # we set the seed so that our splits are the same
  > set.seed(3)
  > ntrain <- round(nrow(PID)*4/5)
  > train <- sample(1:nrow(PID), ntrain)
  > training <- PID[train,]
  > testing <- PID[-train,]

Now we have to choose how many nearest neighbors we want to use. Luckily, there's a great function called knnEval from the chemometrics package that will allow us to graphically visualize the effectiveness of k-NN with a different k using cross-validation. Our objective measures of effectiveness will be the misclassification rate, or, the percent of testing observations that are misclassified.

  > resknn <- knnEval(scale(PID[,-9]), PID[,9], train, kfold=10,
  +                   knnvec=seq(1,50,by=1),
  +                   legpos="bottomright")

There's a lot here to explain! The first three arguments are the predictor matrix, the variables to predict, and the indices of the training data set respectively. Note that the ninth column of the PID data frame holds the class labels—to get a matrix containing just the predictors, we can remove the ninth column by using a negative column index. The scale function that we call on the predictor matrix subtracts each value in each column by the column's mean and divides each value by their respective column's standard deviation—it converts each value to a z-score! This is usually important in k-NN in order for the distances between data points to be meaningful. For example, the distance between data points would change drastically if a column previously measured in meters were re-represented as millimeters. The scale function puts all the features in comparable ranges regardless of the original units.

Note that for the third argument, we are not supplying the function with the training data set, but the indices that we used to construct the training data set. If you are confused, inspect the various objects we have in our workspace with the head function.

The final three arguments indicate that we want to use a 10-fold cross-validation, check every value of k from 1 to 50, and put the legend in the lower-left corner of the plot.

The plot that this code produces is shown in Figure 9.4:

Figure 9.4: A plot illustrating test set error, cross-validated error, and training set error as a function of k in k-NN. After about k=15, the test and CV error doesn't appear to change much

As you can see from the preceding plot, after about k=15, the test and cross-validated misclassification error don't seem to change much. Using k=27 seems like a safe bet, as measured by the minimization of CV error.

Note

To see what it looks like when we underfit and use too many neighbors, check out Figure 9.5, which expands the x-axis of the last figure to show the misclassification error of using up to 200 neighbors. Notice that the test and CV error start off high (at 1-NN) and quickly decrease. At about 70-NN, though, the test and CV error start to rise steadily as the classifier underfits. Note also that the training error starts out at 0 for 1-NN (as we would expect), but very sharply quickly increases as we add more neighbors. This is a good reminder that our goal is not to minimize the training set error but to minimize error on an independent dataset—either a test set or an estimate using cross-validation.

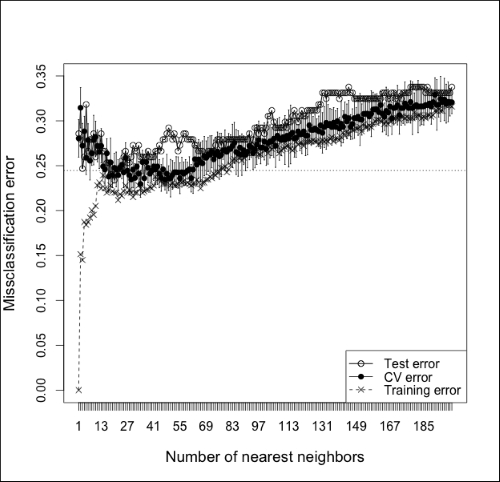
Figure 9.5: A plot illustrating test set error, cross-validated error, and training set error and a function of k in k-NN up to k=200. Notice how error increases as the number of neighbors becomes too large and causes the classifier to overfit.

Let's perform the k-NN!

  > predictions <- knn(scale(training[,-9]),
  +                    scale(testing[,-9]),
  +                    training[,9], k=27)
  > 
  > # function to give correct classification rate
  > accuracy <- function(predictions, answers){
  +   sum((predictions==answers)/(length(answers)))
  + }
  > 
  > accuracy(predictions, testing[,9])
  [1] 0.7597403

It looks like using 27-NN gave us a correct classification rate of 76% (a misclassification rate of 100% - 76% = 24%). Is that good? Well, let's put it in perspective.

If we randomly guessed whether each testing observation was positive for diabetes, we would expect a classification rate of 50%. But remember that the number of non-diabetes observations outnumber the number of observations of diabetes (non-diabetes observations are 65% of the total). So, if we built a classifier that just predicted no diabetes for every observation, we would expect a 65% correct classification rate. Luckily, our classifier performs significantly better than our naïve classifier, although, perhaps, not as good as we would have hoped. As we'll learn as the chapter moves on, k-NN is competitive with the accuracy of other classifiers—I guess it's just a really hard problem!

Confusion matrices

We can get a more detailed look at our classifier's accuracy via a confusion matrix. You can get R to give up a confusion matrix with the following command:

  > table(test[,9], preds)
       preds
        neg pos
    neg  86   9
    pos  28  31

The columns in this matrix represent our classifier's predictions; the rows represent the true classifications of our testing set observations. If you recall from Chapter 3, Describing Relationships, this means that the confusion matrix is a cross-tabulation (or contingency table) of our predictions and the actual classifications. The cell in the top-left corner represents observations that didn't have diabetes that we correctly predicted as non-diabetic (true negatives). In contrast, the cell in the lower-right corner represents true positives. The upper-left cell contains the count of false positives, observations that we incorrectly predicted as having diabetes. Finally, the remaining cell holds the number of false negatives, of which there are 28.

This is helpful for examining whether there is a class that we are systematically misclassifying or whether our false negatives and false positive are significantly imbalanced. Additionally, there are often different costs associated with false negatives and false positives. For example, in this case, the cost of misclassifying a patient as non-diabetic is great, because it impedes our ability to help a truly diabetic patient. In contrast, misclassifying a non-diabetic patient as diabetic, although not ideal, incurs a far less grievous cost. A confusion matrix lets us view, at a glance, just what types of errors we are making. For k-NN, and the other classifiers in this chapter, there are ways to specify the cost of each type of misclassification in order to exact a classifier optimized for a particular cost-sensitive domain, but that is beyond the scope of this book.

Limitations of k-NN

Before we move on, we should talk about some of the limitations of k-NN.

First, if you're not careful to use an optimized implementation of k-NN, classification can be slow, since it requires the calculation of the test data point's distance to every other data point; sophisticated implementations have mechanisms for partially handling this.

Second, vanilla k-NN can perform poorly when the amount of predictor variables becomes too large. In the iris example, we used only two predictors, which can be plotted in two-dimensional space where the Euclidean distance is just the 2-D Pythagorean theorem that we learned in middle school. A classification problem with n predictors is represented in n-dimensional space; the Euclidean distance between two points in high dimensional space can be very large, even if the data points are similar. This, and other complications that arise from predictive analytics techniques using a high-dimensional feature spaces, is, colloquially, known as the curse of dimensionality. It is not uncommon for medical, image, or video data to have hundreds or even thousands of dimensions. Luckily, there are ways of dealing with these situations. But let's not dwell there.