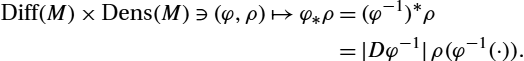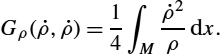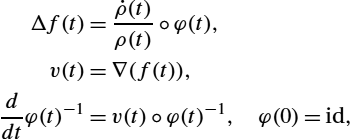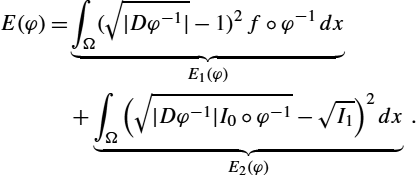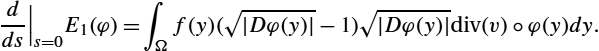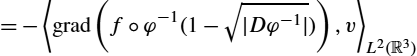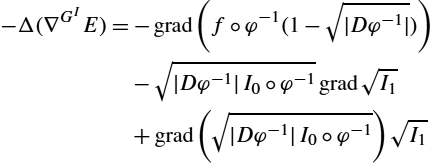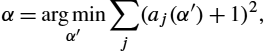Acknowledgements

We thank Caleb Rottmann, who worked on the implementation of the weighted diffeomorphic density matching algorithm. We are grateful for valuable discussions with Boris Khesin, Peter Michor, and François-Xavier Vialard.

This work was partially supported by the grant NIH R01 CA169102, the Swedish Foundation for Strategic Research (ICA12-0052), an EU Horizon 2020 Marie Sklodowska-Curie Individual Fellowship (661482), and by the Erwin Schrödinger Institute program: Infinite-Dimensional Riemannian Geometry with Applications to Image Matching and Shape Analysis by the FWF-project P24625.

16.1 Introduction

Over the last decade image registration has received intense interest, both with respect to medical imaging applications and to the mathematical foundations of the general problem of estimating a transformation that brings two or more given medical images into a common coordinate system [18,22,41,27,39,2,1,13]. In this chapter we focus on a subclass of registration problems referred to as density registration. The primary difference between density registration and general image registration is in how the registration transformation acts on the image being transformed. In density registration the transformation not only deforms the underlying coordinate system, but also scales the image intensity by the local change in volume. In numerous medical imaging applications this is of critical importance and is a fundamental property of the registration problem. The primary motivating clinical application is that of estimating the complex changes in anatomy due to breathing as imaged via 4D respiratory correlated computed tomography (4DRCCT). Given the physical quantitative nature of CT imaging, the natural action of a transformation on a CT image is that of density action: Any local compression induces a corresponding change in local density, resulting in changes in the local attenuation coefficient. We will also see that this difference in action of the transformation on the image being registered has wide ranging implications to the structure of the estimation problem. In this chapter we will study the fundamental geometrical structure of the problem and exemplify its application. The basic outline is as follows: We will first study the abstract mathematical structure of the problem, precisely defining the space of densities and the space of transformation. We will also study the set of transformations that leave the density unchanged. We will see that the explicit characterization of this set of transformations plays a critical role in understanding the geometric structure of the density registration problem. We will then introduce the general (regularized) density matching problem and present efficient numerical algorithms for several specific choices of regularizers. Finally, we will present the before mentioned application to model breathing as imaged via 4D respiratory correlated computed tomography.

16.2 Diffeomorphisms and densities

Let M denote a smooth oriented Riemannian manifold of dimension n with (reference) volume form $\mathrm{d}x$.

As the focus of the chapter is the registration of densities via transformation, the group $\mathrm{Diff}(M)$ of smooth diffeomorphisms of the manifold plays a central role.

The group of diffeomorphisms acts naturally on the space of densities via pullback and pushforward of densities. Indeed, pullback of densities is given by

$\mathrm{Diff}(M)\times \mathrm{Dens}(M)\ni (\phi ,\rho )\mapsto {\phi }^{⁎}\rho =|D\phi |\rho (\phi (\cdot )).$

Notice that this is a right action, that is, ${(\phi \circ \eta )}^{⁎}\rho ={\eta }^{⁎}({\phi }^{⁎}\rho )$. The corresponding left action is given by pushforward of densities

$\mathrm{Diff}(M)\times \mathrm{Dens}(M)\ni (\phi ,\rho )\mapsto {\phi }_{⁎}\rho ={({\phi }^{-1})}^{⁎}\rho =|D{\phi }^{-1}|\rho ({\phi }^{-1}(\cdot )).$

The action of $\mathrm{Diff}(M)$ on densities captures the notion of conservation of mass and is fundamentally different from the standard action of $\mathrm{Diff}(M)$ on functions given by composition (see chapter 4). Indeed, for the density action, we have, for any subset $\mathrm{\Omega }\subset M$,

${\mathrm{Mass}}_{{\phi }_{⁎}\rho }(\phi (\mathrm{\Omega }))={\mathrm{Mass}}_{\rho }(\mathrm{\Omega }),$

which follows from the change-of-coordinates formula for integrals.

The isotropy subgroup of an element $\rho \in \mathrm{Dens}(M)$ is by definition the subgroup of $\mathrm{Diff}(M)$ that leaves the density ρ unchanged. It is given by

${\mathrm{Diff}}_{\rho }(M)=\{\phi \in \mathrm{Diff}(M)|{\phi }_{⁎}\rho =\rho \}.$

The particular case $\rho \equiv 1$ gives the subgroup of volume preserving diffeomorphisms denoted by $\mathrm{SDiff}(M)$. In general, $\phi \in {\mathrm{Diff}}_{\rho }(M)$ implies that φ is mass preserving with respect to ρ. In particular, if $\mathrm{\Omega }\subset M$, then

${\mathrm{Mass}}_{\rho }(\mathrm{\Omega })={\mathrm{Mass}}_{\rho }(\phi (\mathrm{\Omega })).$

The point of diffeomorphic density registration is to select a template density ${\rho }_0\in \mathrm{Dens}(M)$ and then generate new densities by acting on ${\rho }_0$ by diffeomorphisms. In our framework we shall mostly use the left action (by pushforward), but analogous results are also valid for the right action (by pullback). One may ask “Which densities can be reached by acting on ${\rho }_0$ by diffeomorphisms?” In other words, find the range of the mapping

$\mathrm{Diff}(M)\ni \phi \mapsto {\phi }_{⁎}{\rho }_0.$

In the language of group theory it is called the $\mathrm{Diff}(M)$-orbit of ${\rho }_0$. This question was answered in 1965 by Moser [31] for compact manifolds: the result is that the $\mathrm{Diff}(M)$-orbit of ${\rho }_0$ consists of all densities with the same total mass as ${\rho }_0$. This result has been extended to noncompact manifolds [17] and manifolds with boundary [4]. For simplicity, we will only formulate the result in the compact case.

Since the total mass of a density is a positive real number, it follows from Moser's result that the set of $\mathrm{Diff}(M)$-orbits in $\mathrm{Dens}(M)$ can be identified with ${\mathbb{R}}_{+}$. From a geometric point of view, this gives a fibration of $\mathrm{Dens}(M)$ as a fiber bundle over ${\mathbb{R}}_{+}$ where each fiber corresponds to a $\mathrm{Diff}(M)$-orbit. In turn, Moser's result also tells us that each orbit in itself is the base of a principal bundle fibration of $\mathrm{Diff}(M)$. For example, the ${\rho }_0$-orbit can be identified with the quotient $\mathrm{Diff}(M)/{\mathrm{Diff}}_{{\rho }_0}(M)$ through the projection

$\pi :\phi \mapsto {\phi }_{⁎}{\rho }_0.$

See references [29,5] for more details.

16.3 Diffeomorphic density registration

In this part we will describe a general (Riemannian) approach to diffeomorphic density registration, that is, the problem of finding an optimal diffeomorphism φ that transports an α-density ${\rho }_0$ (source) to an α-density ${\rho }_1$ (target). By Moser's result (see Lemma 16.1 and Lemma 16.2) there always exists an infinite-dimensional set of solutions (diffeomorphisms) to this problem. Thus the main difficulty lies in the solution selection. Toward this aim, we introduce the regularized exact α-density registration problem:

In later sections we will introduce several choices for $\mathcal{R}$ and discuss their theoretical and practical properties. In general, we aim to construct regularization terms such that the corresponding registration problem has the following desirable properties:

Note that the notion of meaningful will depend highly on the specific application.

In practice we are sometimes not interested in enforcing the constraint, but are rather interested in a relaxed version of the above problem. Thus we introduce the inexact density registration problem:

On the space of probability densities there exists a canonical Riemannian metric, the Fisher–Rao metric, which allows for explicit formulas of the corresponding geodesic distance: it is given by the (spherical) Hellinger distance. For the purpose of this book chapter, we will often use this distance functional as a similarity measure.

16.4 Density registration in the LDDMM-framework

The LDDMM-framework is based on the idea of using a right-invariant metric on the diffeomorphism group to define the regularity measure, that is,

$\mathcal{R}(\phi )=\mathrm{dist}(\mathrm{id},\phi ),$

where $\mathrm{dist}(\cdot ,\cdot )$ denotes the geodesic distance of a right-invariant metric on $\mathrm{Diff}(M)$. The resulting framework for inexact registration has been discussed for general shape spaces in chapter 4. Therefore we will keep the presentation in this chapter rather brief. Our focus will be on the geometric picture of the exact registration problem in this setup.

From here on we assume that M is equipped with a smooth Riemannian metric g with volume density μ. To define a right-invariant metric on $\mathrm{Diff}(M)$, we introduce the so-called inertia operator $A:\mathfrak{X}(M)\to \mathfrak{X}(M)$, where $\mathfrak{X}(M)$, the set of smooth vector fields, is the Lie algebra of $\mathrm{Diff}(M)$. We will assume that A is a strictly positive elliptic differential operator, that is, self-adjoint with respect to the $L^2$ inner product on $\mathfrak{X}(M)$. For simplicity, we will only consider operators A that are defined via powers of the Laplacian of the Riemannian metric g, that is, we will only consider operators of the form

$A={(1-{\mathrm{\Delta }}_g)}^k$

for some integer k. Here ${\mathrm{\Delta }}_g$ denotes the Hodge–Laplacian of the metric g. Most of the results discussed further are valid for a much larger class of (pseudo)differential operators; see [9]. Any such A defines the inner product $G_{\mathrm{id}}$ on $\mathfrak{X}(M)$ via

$G_{\mathrm{id}}(X,Y)={\int }_{M}g(AX,Y)\mu ,$

where μ denotes the induced volume density of g. We can extend this to a right-invariant metric on $\mathrm{Diff}(M)$ by right-translation:

$G_{\phi }(h,k)=G_{\mathrm{id}}(h\circ {\phi }^{-1},k\circ {\phi }^{-1})={\int }_{M}g(A(h\circ {\phi }^{-1}),k\circ {\phi }^{-1})\mu .$

For an overwiew on right-invariant metrics on diffeomorphism groups, we refer to [28,12,7,8].

In this framework the exact density registration problem reads as follows.

Using this particular regularization term provides an intuitive interpretation of the solution selection: we aim to find the transformation that is as close as possible to the identity under the constraint that it transports the source density to the target density.

In the following theorem we present a summary of the geometric picture that underlies the exact registration problem. To keep the presentation simple, we will only consider the case $\alpha =1$, that is, the standard density action. A similar result can be obtained for general α.

Let π be the projection

$\pi :\mathrm{Diff}(M)\to \mathrm{Dens}(M)\simeq {\mathrm{Diff}}_{\rho }(M)\mathrm{Diff}(M)$

induced by the left action of the diffeomorphism group; see Lemma 16.1. By [9] we have the following:

A direct consequence of the Riemannian submersion picture is the following characterization of the solutions of the exact density registration problem.

16.5 Optimal information transport

In this section we describe an explicit way of solving the exact density registration problem. The framework in this section has been previously developed for random sampling from nonuniform arbitrary distributions [6]. For simplicity, we will restrict ourselves to the standard density action, that is, $\alpha =1$. However, all the algorithms are easily generalized to general α. The specific setting uses deep geometric connections between the Fisher–Rao metric on the space of probability densities and a special right-invariant metric on the group of diffeomorphisms.

The main advantage of the Fisher–Rao metric is the existence of explicit formulas for the solution to the geodesic boundary value problem and thus also for the induced geodesic distance:

Using formula (16.12) for geodesics, we will construct an almost explicit algorithm for solving an exact density registration problem of the form (16.2). To this end, we need to introduce a suitable regularization term. As in the LDDMM framework (see section 16.4), we will choose it as distance to the identity with respect to a right-invariant Riemannian metric on $\mathrm{Diff}(M)$. However, to exploit the explicit formula (16.12), the right-invariant metric needs to communicate with the Fisher–Rao metric, as we now explain.

We are now ready to formulate our special density registration problem, called the optimal information transport problem:

In general, the formula for $d_I(\mathrm{id},\phi )$ is not available explicitly; we would have to solve a nonlinear PDE (the EPDiff equation). However, because of the special relation between $d_I$ and $d_F$, we have the following result, which is the key to an efficient algorithm.

Based on Theorem 16.2, we now give a semiexplicit algorithm for numerical computation of the solution to the optimal information transport problem. The algorithm assumes that we have a numerical way to represent functions, vector fields, and diffeomorphisms on M and numerical methods for

Although it is possible to use optimal information transport and the algorithm above for medical image registration problems, the results so obtained are typically not satisfactory; the diffeomorphism obtained tends to compress and expand matter instead of moving it (see, e.g., [5, Sec. 4.2]). Another problem is that the source and target densities are required to be strictly positive, which is typically not the case for medical images. In section 16.6 we will develop a gradient flow-based approach, which will lead to much better results for these applications. However, in applications where either the source or the target density is uniform (with respect to the natural Riemannian structure of the manifold at hand), the OIT approach can be very competitive, which yields a natural application for random sampling.

16.5.1 Application: random sampling from nonuniform distribution

In this section we describe an application of OIT to random sampling from nonuniform distributions, that is, the following problem.

Random sampling problem

Let ${\rho }_1\in \mathrm{Dens}(M)$. Generate N random samples from the probability distribution ${\rho }_1$.

The classic approach to sample from a probability distribution on a higher-dimensional space is to use Markov chain Monte Carlo (MCMC) methods, for example, the Metropolis–Hastings algorithm [20]. An alternative idea is to use diffeomorphic density registration between the density ${\rho }_1$ and the standard density ${\rho }_0$ from which samples can be drawn easily. Indeed, we can then draw samples from ${\rho }_0$ and transform them via the computed diffeomorphism to generate samples from ${\rho }_1$. A benefit of transport-based methods over traditional MCMC methods is cheap computation of additional samples; it amounts to drawing uniform samples and then evaluating the transformation. On the other hand, unlike MCMC, transport-based methods scale poorly with increasing dimensionality of M.

Moselhy and Marzouk [30] and Reich [33] proposed to use optimal mass transport (OMT) to construct the desired diffeomorphism φ, thereby enforcing $\phi =\mathrm{\nabla }c$ for some convex function c. The OMT approach implies solving, in one form or another, the heavily nonlinear Monge–Ampere equation for c. A survey of the OMT approach to random sampling is given by Marzouk et al. [26]. Using OIT instead of OMT, the problem simplifies significantly, as the OIT-algorithm only involves solving linear Poisson problems.

As a specific example, consider $M={\mathbb{T}}^2\simeq {(\mathbb{R}/2\pi \mathbb{Z})}^2$ with distribution defined in Cartesian coordinates $x,y\in [-\pi ,\pi )$ by

$\rho \sim 3\exp (-x^2-10{(y-x^2/2+1)}^2)+1/10,$

(16.20)

normalized so that the ratio between the maximum and mimimum of ρ is 100. The resulting density is depicted in Fig. 16.1 (left).

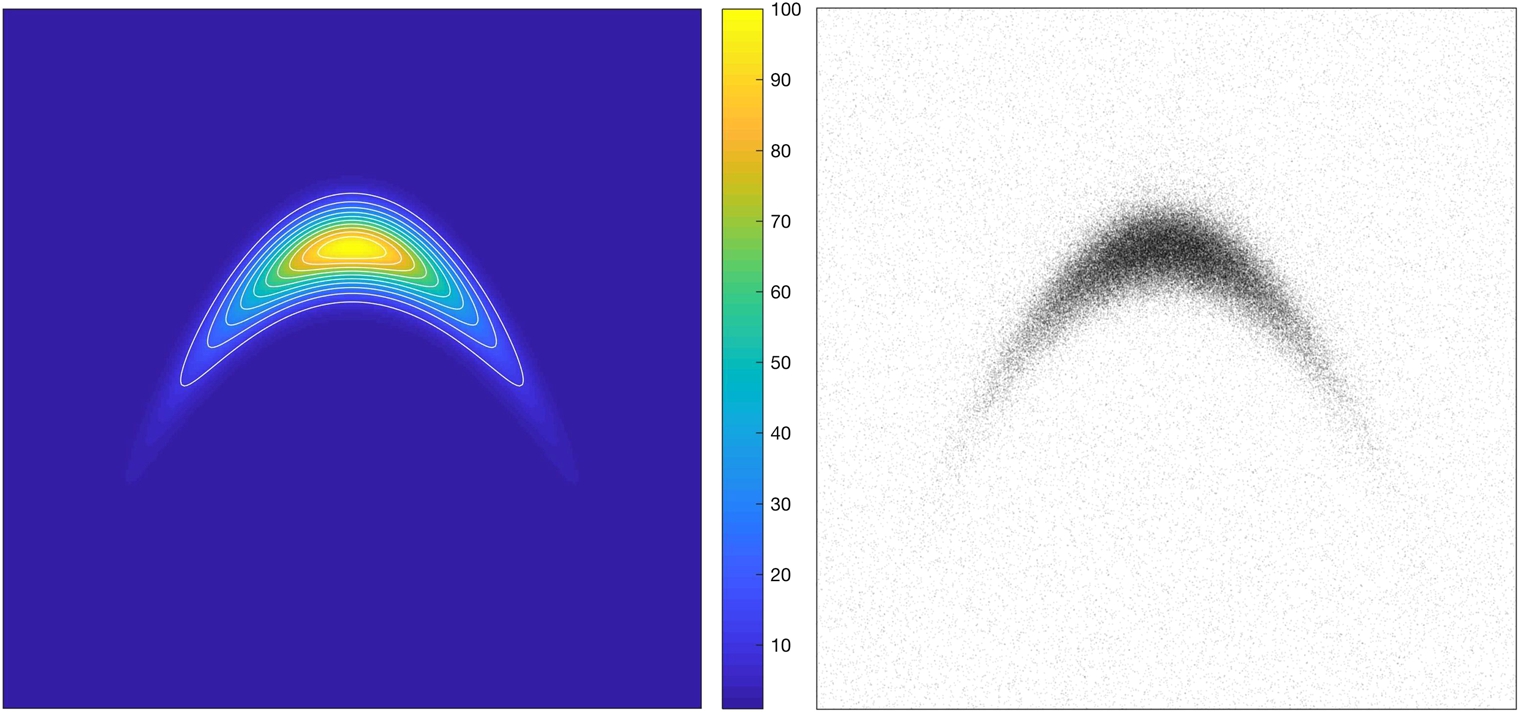
We draw 10⁵ samples from this distribution using a MATLAB implementation of our algorithm, available under MIT license at https://github.com/kmodin/oit-random

The implementation can be summarized as follows. To solve the Poisson problem, we discretize the torus by a $256\times 256$ mesh and use the fast Fourier transform (FFT) to invert the Laplacian. We use 100 time steps. The resulting diffeomorphism is shown as a mesh warp in Fig. 16.2. We then draw 10⁵ uniform samples on ${[-\pi ,\pi ]}^2$ and apply the diffeomorphism on each sample (applying the diffeomorphism corresponds to interpolation on the warped mesh). The resulting random samples are depicted in Fig. 16.1 (right). Drawing new samples is very efficient. For example, another 10⁷ samples can be drawn in less than a second.

16.6 A gradient flow approach

In the optimal information transport described in the previous section the fundamental restriction is that the volume form of Riemannian metric of the base manifold is compatible with the density being transformed in that it has to be conformally related to the source density ${\rho }_0$. In most medical imaging applications this modeling assumption is not applicable. In this section we will develop more general algorithms that relax the requirement for the metric to be compatible with the densities to be registered. We will consider the natural extension of the Fisher–Rao metric to the space of all densities and the case where $\mathrm{d}x(\mathrm{\Omega })=\infty$, for which it is given by

$d_F^2(I_{0}dx,I_{1}dx)={\int }_{\mathrm{\Omega }}{(\sqrt{I_0}-\sqrt{I_1})}^{2}dx.$

Notice that $d_F^2(\cdot ,\cdot )$ in this case is the Hellinger distance. For details, see [5].

The Fisher–Rao metric is the unique Riemannian metric on the space of probability densities that is invariant under the action of the diffeomorphism group [7,3]. This invariance property extends to the induced distance function, so

$d_F^2(I_{0}dx,I_{1}dx)=d_F^2({\phi }_{⁎}(I_{0}dx),{\phi }_{⁎}(I_{1}dx))\forall \phi \in \mathrm{Diff}(\mathrm{\Omega }).$

Motivated by the aforementioned properties, we develop a weighted diffeomorphic registration algorithm for registration of two density images. The algorithm is based on the Sobolev $H^1$ gradient flow on the space of diffeomorphisms that minimizes the energy functional

$E(\phi )=d_F^2({\phi }_{⁎}(fdx),(f\circ {\phi }^{-1})dx)+d_F^2({\phi }_{⁎}(I_{0}dx),I_{1}dx).$

This energy functional is only a slight modification of the energy functional studied in [5]. Indeed, if f in the equation is a constant $\sigma >0$, then (16.23) reduces to the energy functional of Bauer, Joshi, and Modin [5, § 5.1]. Moreover, the geometry described in [5, § 5.3] is valid also for the functional (16.23), and, consequently, the algorithm developed in [5, § 5.2] can be used also for minimizing (16.23). There the authors view the energy functional as a constrained minimization problem on the product space $\mathrm{Dens}(\mathrm{\Omega })\times \mathrm{Dens}(\mathrm{\Omega })$ equipped with the product distance; see Fig. 16.3 and [5, § 5] for details on the resulting geometric picture. Related work on diffeomorphic density registration using the Fisher Rao metric can be found in [37,36].

Using the invariance property of the Fisher–Rao metric and assuming infinite volume, the main optimization problem associated with the energy functional (16.23) is the following.

The invariance of the Fisher–Rao distance can be seen with a simple change of variables $x\mapsto \phi (y)$, $dx\mapsto |D\phi |dy$, and $|D{\phi }^{-1}|\mapsto \frac{1}{|D\phi |}$. Then, Equation (16.24) becomes

$E(\phi )={\int }_{\mathrm{\Omega }}{(1-\sqrt{|D\phi |})}^{2}fdy+{\int }_{\mathrm{\Omega }}{(\sqrt{I_0}-\sqrt{|D\phi |I_1\circ \phi })}^{2}dy.$

To better understand the energy functional $E(\phi )$, we consider the two terms separately. The first term $E_1(\phi )$ is a regularity measure for the transformation. It penalizes the deviation of the diffeomorphism φ from being volume preserving. The density $fdx$ acts as a weighting on the domain Ω; that is, change of volume (compression and expansion of the transformation φ) is penalized more in regions of Ω where f is large. The second term $E_2(\phi )$ penalizes dissimilarity between $I_{0}dx$ and ${\phi }^{⁎}(I_{1}dx)$. It is the Fisher–Rao distance between the initial density $I_{0}dx$ and the transformed target density ${\phi }^{⁎}(I_{1}dx)$. Because of the invariance (16.22) of the Fisher–Rao metric, this is the same as the Fisher–Rao distance between $I_{1}dx$ and ${\phi }_{⁎}(I_{0}dx)$.

Solutions to problem (16.24) are not unique. To see this, let ${\mathrm{Diff}}_I(\mathrm{\Omega })$ denote the space of all diffeomorphisms preserving the volume form $Idx$:

${\mathrm{Diff}}_I(\mathrm{\Omega })=\{\phi \in \mathrm{Diff}(\mathrm{\Omega })||D\phi |(I\circ \phi )=I\}.$

If φ is a minimizer of $E(\cdot )$, then $\psi \circ \phi$ for any

$\psi \in {\mathrm{Diff}}_{1,I_0}(\mathrm{\Omega })≔{\mathrm{Diff}}_1(\mathrm{\Omega })\cap {\mathrm{Diff}}_{I_0}(\mathrm{\Omega })$

is also a minimizer. Notice that this space is not trivial. For example, any diffeomorphism generated by a Nambu–Poisson vector field (see [32]), with $I_0$ as one of its Hamiltonians, will belong to it. A strategy to handle the degeneracy was developed in [5, § 5]: the fact that the metric is descending with respect to the $H^1$ metric on $\mathrm{Diff}(\mathrm{\Omega })$ can be used to ensure that the gradient flow is infinitesimally optimal, that is, always orthogonal to the null-space. We employ the same strategy in this paper. The corresponding geometric picture can be seen in Fig. 16.3.

To derive an gradient algorithm to optimize the energy functional the natural metric on the space of diffeomorphisms to use is the $H^1$-metric due to its intimate link with the Fisher–Rao metric as described previously. The $H^1$-metric on the space of diffeomorphisms is defined using the Hodge Laplacian on vector fields and is given by

$G_{\phi }^I(U,V)={\int }_{\mathrm{\Omega }}\langle -\mathrm{\Delta }u,v\rangle dx.$

Due to its connections to information geometry, we also refer to this metric as the information metric. Let ${\mathrm{\nabla }}^{G^I}E$ denote the gradient with respect to the information metric defined previously. Our approach for minimizing the functional of (16.25) is to use a simple Euler integration of the time discretization of the gradient flow:

$\dot{\phi }=-{\mathrm{\nabla }}^{G^I}E(\phi ).$

The resulting final algorithm is one order of magnitude faster than LDDMM, since we are not required to time integrate the geodesic equations, as is necessary in LDDMM [42].

In the following theorem we calculate the gradient of the energy functional.

16.6.1 Thoracic density registration

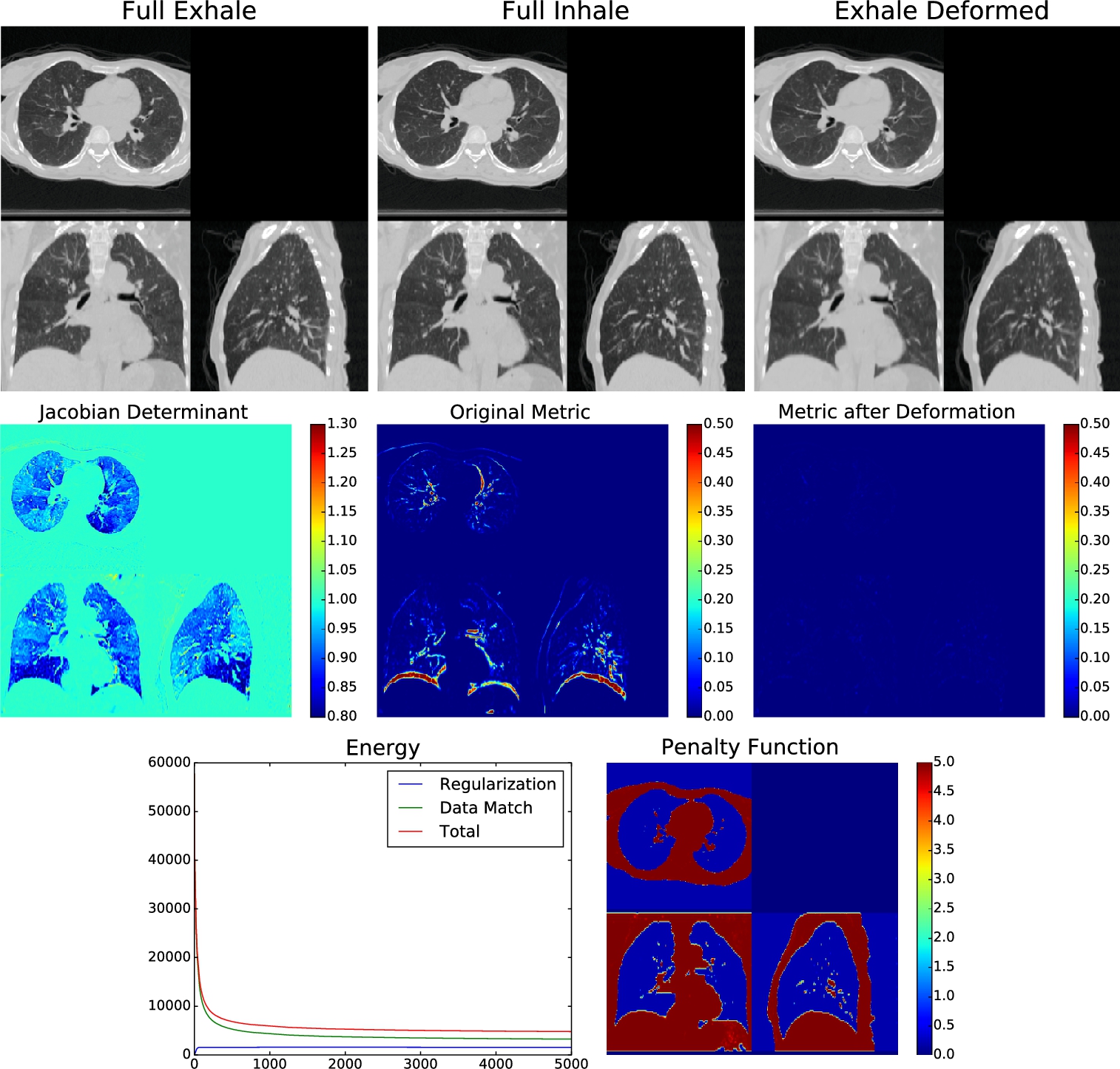
We now present an application of the developed theory to the problem of estimating complex anatomical deformations associated with the breathing cycle as imaged via computed tomography (CT) [16]. This problem has wide-ranging medical applications, in particular, radiation therapy of the lung, where accurate estimation of organ deformations during treatment impacts dose calculation and treatment decisions [35,23,38,15]. The current state-of-the-art radiation treatment planning involves the acquisition of a series of respiratory correlated CT (RCCT) images to build 4D (three spatial and one temporal) treatment planning data sets. Fundamental to the processing and clinical use of these 4D data sets is the accurate estimation of registration maps that characterize the motion of organs at risk and the target tumor volumes.

The 3D image produced from X-ray CT is an image of linear attenuation coefficients. For narrow beam X-ray, the linear attenuation coefficient (LAC) for a single material (units ${\text{cm}}^{-1}$) is defined as $\mu (x)=m\rho (x)$, where m is a material-specific property called the mass attenuation coefficient (units ${\text{cm}}^2/\mathrm{g}$) that depends on the energy of the X-ray beam. The linear attenuation coefficient is proportional to the true density and therefore exhibits conservation of mass. Unfortunately, CT image intensities do not represent true narrow beam linear attenuation coefficients. Instead, modern CT scanners use wide beams that yield secondary photon effects at the detector. CT image intensities reflect effective linear attenuation coefficients as opposed to the true narrow beam linear attenuation coefficient.

To see the relationship between effective LAC and true narrow beam LAC, we ran a Monte Carlo simulation using an X-ray spectrum and geometry from a Philips CT scanner at various densities of water (since lung tissue is very similar to a mixture between water and air) [11]. The nonlinear relationship between effective LAC and narrow beam LAC relationship is clear (see Fig. 16.4).

If we have conservation of mass within a single subject in a closed system, then we expect an inverse relationship between average density in a region Ω and volume of that region: $D_t=\frac{M}{V_t}$. Here $V_t={\int }_{{\mathrm{\Omega }}_t}1dx$, $D_t={\int }_{{\mathrm{\Omega }}_t}{I}_t(x)dx/V_t$, ${\mathrm{\Omega }}_t$ is the domain of the closed system (that moves over time), and t is a phase of the breathing cycle. This relationship becomes linear in log space with a slope of −1:

$\ln (D_t)=\ln (M)-\ln (V_t)$

(16.43)

Our experimental results confirm the Monte Carlo simulation in that lungs imaged under CT do not follow this inverse relationship. Rather, the slope found in these datasets in log space is consistently greater than −1 (see Fig. 16.6). This implies that for real clinical CT data sets, the lung tissue is acted on by an α-density action. Using the isomorphism between α-densities and 1-densities, we estimate the power transformation $I(x)\mapsto I{(x)}^{\alpha }$ and estimate the α that yields the best conservation of mass property.

For each subject, we perform a linear regression of the measured LAC density in the homogeneous lung region and the calculated volume in log space. Let $\mathit{d}(\alpha )=\log ({\int }_{{\mathrm{\Omega }}_t}{I}_t{(x)}^{\alpha }dx/{\int }_{{\mathrm{\Omega }}_t}1dx)$ (the log density) and $\overrightarrow{v}=\log ({\int }_{{\mathrm{\Omega }}_t}1dx)$ (the log volume), where again t is a breathing cycle timepoint. The linear regression then models the relationship in log space as $\mathit{d}(\alpha )\approx a\overrightarrow{v}+b$. Let $a_j(\alpha )$ be the slope solved for in this linear regression for the jth subject. To find the optimal α for the entire dataset, we solve

$\alpha =\underset{{\alpha }^{\prime }}{\mathrm{arg\hspace{0.17em}min}}\sum _j{(a_j({\alpha }^{\prime })+1)}^2,$

(16.44)

which finds the value of α that gives us an average slope closest to −1.

Applying this power function to the CT data allows us to perform our density registration algorithm based on the theory developed. We therefore seek to minimize the energy functional described in the previous section, given by

$E(\phi )=d_F^2({\phi }_{⁎}(fdx),(f\circ {\phi }^{-1})dx)+d_F^2({\phi }_{⁎}(I_{0}dx),I_{1}dx))$

(16.45)

$$\begin{gathered} =\underset{E_1(\phi )}{\underbrace{{\int }_{\mathrm{\Omega }}{(\sqrt{|D{\phi }^{-1}|}-1)}^{2}f\circ {\phi }^{-1}dx}} \\ +\underset{E_2(\phi )}{\underbrace{{\int }_{\mathrm{\Omega }}{(\sqrt{|D{\phi }^{-1}|I_0\circ {\phi }^{-1}}-\sqrt{I_1})}^{2}dx}}. \end{gathered}$$

(16.46)

We construct the density $f(x)dx$, a positive weighting on the domain Ω, to model the physiology of the thorax: regions where $f(x)$ is high have a higher penalty on nonvolume-preserving deformations and regions where $f(x)$ is low have a lower penalty on nonvolume-preserving deformations. Physiologically, we know that the lungs are quite compressible as air enters and leaves. Surrounding tissue including bones and soft tissue, on the other hand, is essentially incompressible. Therefore our penalty function $f(x)$ is low inside the lungs and outside the body and high elsewhere. For our penalty function, we simply implement a sigmoid function of the original CT image: $f(x)=\mathrm{sig}(I_0(x))$.

Recall the Sobolev gradient calculated in Theorem 16.30 with respect to the energy functional given by

$\delta E=-{\mathrm{\Delta }}^{-1}(-\mathrm{\nabla }(f\circ {\phi }^{-1}(1-\sqrt{|D{\phi }^{-1}|}))-\sqrt{|D{\phi }^{-1}|I_0\circ {\phi }^{-1}}\mathrm{\nabla }(\sqrt{I_1})+\mathrm{\nabla }(\sqrt{|D{\phi }^{-1}|I_0\circ {\phi }^{-1}}\left)\sqrt{I_1}\right).$

(16.47)

Then the current estimate of ${\phi }^{-1}$ is updated directly via an Euler integration of the gradient flow [34]:

${\phi }_{j+1}^{-1}(x)={\phi }_j^{-1}(x+ϵ\delta E)$

(16.48)

for some step size ϵ. Since we take the Sobolev gradient, the resulting deformation is guaranteed to be invertible with a sufficiently small ϵ. Also notice that the gradient only depends on ${\phi }^{-1}$, so there is no need to keep track of both φ and ${\phi }^{-1}$. The exact numerical algorithm is as follows:

Numerical algorithm for weighted diffeomorphic density registration

The algorithm was implemented using the PyCA package and can be downloaded at https://bitbucket.org/crottman/pycaapps/src/master/ See the application Weighted Diffeomorphic Density Registration.

For the DIR dataset, we solved for the exponent that yields conservation of mass, which yielded $\alpha =0.60$ giving us the best fit. Without using the exponential fit, the average slope of log density log volume plot was −0.66 (SD 0.048). After applying the exponential to the CT intensities, the average slope is −1.0 (SD 0.054). The log–log plots of all ten patients in the DIR dataset and the box plots of the slope are shown in Fig. 16.5.

For the 30 subject dataset, we solved for $\alpha =0.52$, which gives us conservation of mass. Without using the exponential fit, the average slope of the log–log plot was −0.59 (SD 0.11).

We applied our proposed weighted density registration algorithm to the first subject from the DIR dataset. This subject has images at 10 timepoints and has a set of 300 corresponding landmarks between the full inhale image and the full exhale image. These landmarks were manually chosen by three independent observers. Without any deformation, the landmark error is 4.01 mm (SD 2.91 mm). Using our method, the landmark error is reduced to 0.88 mm (SD 0.94 mm), which is only slightly higher than the observer repeat registration error of 0.85 mm (SD 1.24 mm).

We implement our algorithm on the GPU and plot the energy and the Fisher–Rao metric with and without applying the deformation. These results are shown in Fig. 16.6. In this figure we show that we have excellent data match, whereas the deformation remains physiologically realistic: inside the lungs there is substantial volume change due to respiration, but the deformation outside the lungs is volume preserving. With a $256\times 256\times 94$ voxel dataset, our algorithm takes approximately nine minutes running for four thousand iterations on a single nVidia Titan Z GPU.