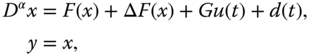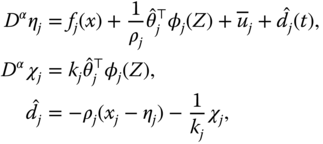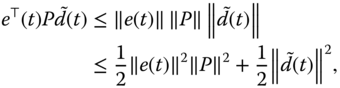Chapter 6
Disturbance-Observer-Based Neural Control for Uncertain Fractional-Order Rotational Mechanical System
6.1 Problem Statement
On the basis of the Caputo definition of the fractional derivative (2.17), we consider the following fractional-order rotational mechanical system with a centrifugal governor in the following form [226]:
where ![]() is the fractional order with
is the fractional order with ![]() ,
, ![]() ,
, ![]() and
and ![]() are the state variables of the fractional-order system (6.1),
are the state variables of the fractional-order system (6.1), ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are known constants,
are known constants, ![]() , and
, and ![]() .
.
From Equation (6.1), the fractional-order nonlinear model of a rotational mechanical system with a centrifugal governor in the presence of unknown uncertainties, external disturbances, and control inputs can be described as follows:
where ![]() is the fractional order with
is the fractional order with ![]() ,
, ![]() is a known control gain matrix and
is a known control gain matrix and ![]() is an invertible matrix,
is an invertible matrix, ![]() is the state vector of the fractional-order system (6.2),
is the state vector of the fractional-order system (6.2), ![]() is the known nonlinear function vector with
is the known nonlinear function vector with ![]() ,
, ![]() , and
, and ![]() ,
, ![]() is the unknown nonlinear uncertainty,
is the unknown nonlinear uncertainty, ![]() is the control input,
is the control input, ![]() is the external disturbance, and
is the external disturbance, and ![]() is the system output vector.
is the system output vector.
In this chapter, we design a nonlinear FODO-based adaptive neural control scheme to track the desired output of the uncertain FONS (6.2). The radial basis function neural network is used to approximate unknown nonlinear functions in the uncertain FONS (6.2) with external disturbances. On the basis of the proposed control scheme, the signal ![]() could follow a given desired trajectory
could follow a given desired trajectory ![]() in the presence of system uncertainties and unknown external disturbances. The proposed control scheme will be rigorously shown to guarantee that all the signals in the closed-loop system remain bounded.
in the presence of system uncertainties and unknown external disturbances. The proposed control scheme will be rigorously shown to guarantee that all the signals in the closed-loop system remain bounded.
To proceed with the design of the robust adaptive neural control for the uncertain FONS (6.2) subjected to external disturbances, the following assumptions are required.
6.2 Adaptive Neural Control Design
6.2.1 Design of Fractional-Order Disturbance Observer
Without loss of generality, according to the uncertain FONS (6.2), we have
where ![]() is the
is the ![]() th element of
th element of ![]() ,
, ![]() is the
is the ![]() th element of
th element of ![]() ,
, ![]() is the
is the ![]() th element of
th element of ![]() ,
, ![]() is the
is the ![]() th element of
th element of ![]() with
with ![]() ,
, ![]() is the
is the ![]() th element of
th element of ![]() , and
, and ![]() .
.
On the basis of Lemma 2.4, the neural network is employed to approximate ![]() with
with ![]() , and we obtain
, and we obtain
where ![]() .
.
Since the disturbance ![]() in Equation (6.2) is unknown,
in Equation (6.2) is unknown, ![]() cannot be applied to develop robust tracking control for the uncertain FONS (6.2). To overcome this problem, a nonlinear FODO is designed to estimate disturbance.
cannot be applied to develop robust tracking control for the uncertain FONS (6.2). To overcome this problem, a nonlinear FODO is designed to estimate disturbance.
For the system (6.4), the nonlinear FODO is designed as follows:
where ![]() and
and ![]() are the state variables of the nonlinear FODO,
are the state variables of the nonlinear FODO, ![]() is the output of the disturbance observer, and the adaptive law
is the output of the disturbance observer, and the adaptive law ![]() will be described in the next section.
will be described in the next section.
According to Equations (6.4) and (6.5), we have

where ![]() ,
, ![]() is the disturbance estimation error, and
is the disturbance estimation error, and ![]() .
.
Differentiating ![]() and considering Equation (6.5) yields
and considering Equation (6.5) yields
6.2.2 Controller Design and Stability Analysis
This section develops a nonlinear FODO-based adaptive neural tracking control scheme for the uncertain FONS (6.2). The tracking error is defined as
where ![]() is the tracking error vector and
is the tracking error vector and ![]() is the desired signal vector.
is the desired signal vector.
According to Equation (6.8), the dynamic of the tracking error can be written as
On the basis of these discussions, the tracking controller and the adaptive update law will be designed to ensure that the error system (6.9) is ultimately bounded stable. We first consider the following Lyapunov function candidate:
where ![]() is a symmetric and positive definite constant matrix and
is a symmetric and positive definite constant matrix and ![]() is a design constant.
is a design constant.
In particular, we have
Invoking Equations (6.10) and (6.11), Lemma 2.1, and Lemma 2.5, we obtain
Substituting Equation (6.9) into Equation (6.12), we have

On the basis of Lemma 2.4, the neural network is used to approximate ![]() with
with ![]() , and we obtain
, and we obtain
where
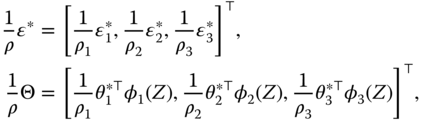
and ![]() .
.
The adaptive neural controller is designed as
where ![]() is a design constant and
is a design constant and
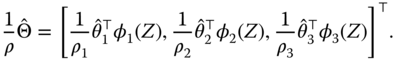
Substituting Equation (6.15) into Equation (6.14), we have
where

![]() , and
, and ![]() .
.
Furthermore, the adaptive law for ![]() is chosen as
is chosen as
where ![]() and
and ![]() are design constants, and
are design constants, and ![]() denotes the
denotes the ![]() th element of
th element of ![]() , with
, with ![]() .
.
According to Equation (6.17) and Lemma 2.5, we have
From Equation (6.18), Equation (6.16) can be rewritten as
with
where ![]() and
and ![]() is an unknown constant.
is an unknown constant.
Substituting Equations (6.20) and (6.21) into Equation (6.19), we have
with
Combining Equations (6.22) and (6.23), we obtain
Invoking Assumption 6.2 and Equation (6.7), Equation (6.24) can be written as
According to Equation (6.25), we have
where ![]() and
and ![]() .
.
Furthermore, Equation (6.26) can be rewritten as
From Equation (6.27), we obtain

where ![]() ,
,
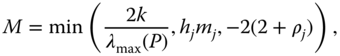
and
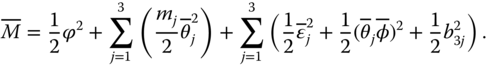
This design procedure can be summarized in the following theorem, which contains the results of the FODO-based adaptive neural control for the uncertain FONS (6.2) with unknown time-varying external disturbance.
6.3 Simulation Example
In this section, simulation results are presented to illustrate the effectiveness of the proposed robust adaptive neural control scheme for the uncertain FONS with external disturbances. From Equation (6.1), the fractional-order nonlinear model of a rotational mechanical system with a centrifugal governor in the presence of unknown uncertainties, external disturbances, and control inputs can be described as follows:
where ![]() is the
is the ![]() th line of
th line of ![]() .
.
In this simulation, the fractional order is chosen as ![]() , the initial conditions of system (6.32) are chosen as
, the initial conditions of system (6.32) are chosen as ![]() , and the system parameters are selected as
, and the system parameters are selected as ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . The control parameters are chosen as
. The control parameters are chosen as ![]() ,
, ![]() , and
, and ![]() , with
, with ![]() . The matrices are designed as
. The matrices are designed as ![]() and
and ![]() . The uncertainty terms are assumed as
. The uncertainty terms are assumed as ![]() ,
, ![]() and
and ![]() . The desired trajectories are chosen as
. The desired trajectories are chosen as ![]() ,
, ![]() , and
, and ![]() . The external disturbances are assumed as
. The external disturbances are assumed as ![]() ,
, ![]() , and
, and ![]() . On the basis of the result of Ishtev [225], we have
. On the basis of the result of Ishtev [225], we have ![]() , where
, where ![]() denotes the square root of minus one and
denotes the square root of minus one and ![]() and
and ![]() are arbitrary numbers. In this simulation, the parameter is assumed as
are arbitrary numbers. In this simulation, the parameter is assumed as ![]() and the fractional order is chosen as
and the fractional order is chosen as ![]() . Thus,
. Thus, ![]() can be applied to approximate
can be applied to approximate ![]() . The comparison result is shown in Figure 6.1 for the case of
. The comparison result is shown in Figure 6.1 for the case of ![]() and
and ![]() . According to Figure 6.1, Assumption 6.1 and Assumption 6.2 are satisfied.
. According to Figure 6.1, Assumption 6.1 and Assumption 6.2 are satisfied.

Figure 6.1 Comparison result of  and
and  .
.
The simulation results of the uncertain FONS (6.32) with external disturbances are shown in Figure 6.2, Figure 6.3, Figure 6.4, Figure 6.5, and Figure 6.6 under the proposed adaptive neural control scheme. The tracking results of output signals and desired signals are given in Figure 6.2a–c. It is shown that the tracking performance is satisfactory. Figure 6.3 shows that the tracking errors ![]() ,
, ![]() , and
, and ![]() are bounded. Furthermore, the estimate performance of the proposed nonlinear FODO (6.5) is presented in Figure 6.4 and Figure 6.5. It is evident from Figure 6.4 and Figure 6.5 that the disturbance observer is effective and feasible. The control input signals, which are bounded, are shown in Figure 6.6. It is concluded from these simulation results that the proposed adaptive neural control technique is effective for uncertain fractional-order nonlinear systems using FODOs.
are bounded. Furthermore, the estimate performance of the proposed nonlinear FODO (6.5) is presented in Figure 6.4 and Figure 6.5. It is evident from Figure 6.4 and Figure 6.5 that the disturbance observer is effective and feasible. The control input signals, which are bounded, are shown in Figure 6.6. It is concluded from these simulation results that the proposed adaptive neural control technique is effective for uncertain fractional-order nonlinear systems using FODOs.

Figure 6.2 Output  of the system (6.32) follows the desired trajectory
of the system (6.32) follows the desired trajectory  : (a)
: (a)  and
and  ; (b)
; (b) 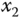 and
and  ; (c)
; (c)  and
and 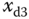 .
.

Figure 6.3 Tracking errors 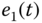 ,
,  , and
, and  for desired trajectories
for desired trajectories 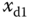 ,
, 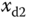 and
and  .
.

Figure 6.4 Disturbance  and approximation output of
and approximation output of  : (a)
: (a)  and
and 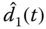 ; (b)
; (b)  and
and  ; (c)
; (c)  and
and  .
.

Figure 6.5 Disturbance estimation errors  ,
, 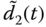 , and
, and 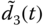 .
.

Figure 6.6 Control inputs  ,
,  , and
, and  of the system (6.32).
of the system (6.32).
6.4 Conclusion
An adaptive neural tracking control has been proposed for a class of uncertain fractional-order nonlinear systems in this chapter. To improve the ability of disturbance attenuation and the control performance of the FONS subjected to external unknown bounded disturbances and model uncertainties, the fractional-order nonlinear disturbance observer together with neural network approximation has been employed to estimate the disturbance. By using the designed nonlinear FODO and the neural network, the FODO-based adaptive neural network control has been developed for uncertain fractional-order nonlinear systems with external disturbances. The stability of the closed-loop system has been proved based on the fractional-order Lyapunov method. Finally, simulation results have been presented to illustrate the effectiveness of the proposed adaptive neural control scheme.