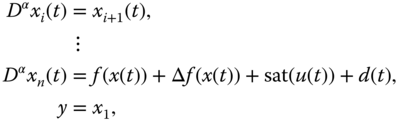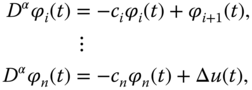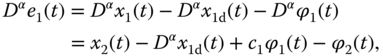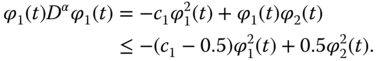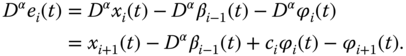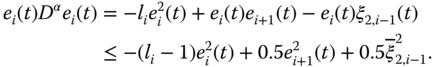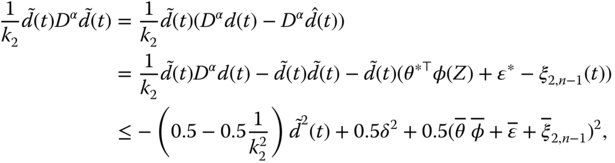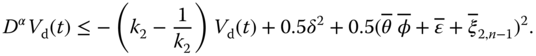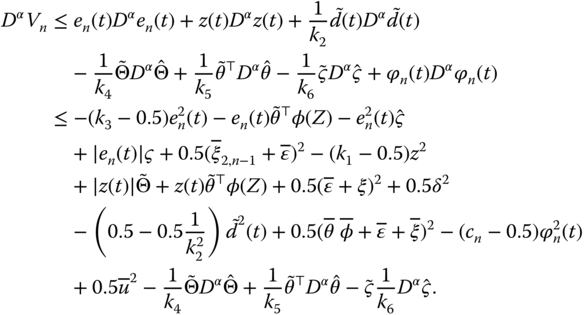Chapter 7
Adaptive Neural Tracking Control for Uncertain Fractional-Order Chaotic Systems Subject to Input Saturation and Disturbance
7.1 Problem Statement
According to the Caputo definition of the fractional derivative (2.17), the following uncertain FOCS in the presence of input saturation and unknown external disturbance is described as follows:
where 
is the fractional order with 
, 
is the fractional derivative, 
are the state variables of the chaotic system, which are measurable, 
is the system output, 
is the desired control input, 
is the unknown time-varying disturbance, 
is the known nonlinear function with 
, 
is the unknown nonlinear function, and 
is the input saturation function defined as follows:
where 
is a known bound of 
and 
is the standard sign function.
The aim of this chapter is to design a SMFODO to approximate the unknown external disturbance, and to propose an adaptive neural control scheme based on the designed SMFODO to control the output signal of the uncertain FOCS (7.1), which could follow a given desired trajectory 
in the presence of input saturation and unknown external disturbance. Meanwhile, the proposed control scheme will be rigorously shown to guarantee that all the signals in the closed-loop system remain bounded.
To facilitate the design of the neural tracking control for the uncertain FOCS (7.1) subjected to input saturation and external disturbance, the following assumptions are necessary in this study.
7.2 Adaptive Neural Control Design Based on Fractional-Order Disturbance Observer
In this section, an adaptive neural control will be proposed for an uncertain FOCS with unknown external disturbance and input saturation based on the designed SMFODO. To handle the input saturation, the following auxiliary system with the same order as the FOCS (7.1) is constructed to counteract the effect of the input saturation, as follows:
where 
are the state variables of the auxiliary system, 
are the design constants, and 
.
Using the state variables of the auxiliary system (7.3), the adaptive neural control scheme is designed using the backstepping technique. The detailed design process is given as follows.
Step 1
In the first step, we define the error variable as 
and 
, where 
is the virtual control law and will be designed.
Considering Equations (7.1) and (7.3), we obtain
Invoking the definition of 
, Equation (7.4) can be written as
Furthermore, the virtual control law 
in the first step is designed as
where 
is a design constant.
Substituting Equation (7.6) into Equation (7.5) yields
From Equation (7.7), we have
According to Equation (7.3), we obtain
Considering the signals 
and 
, the Lyapunov function candidate is chosen as
On the basis of Lemma 2.1, the Caputo derivative of 
can be described as
Invoking Equations (7.8) (7.9), and (7.11), we have
where 
and 
will be handled in the next step.
Step 
Define the error variable as 
and 
, where 
and 
are the virtual control laws designed in the 
th step and the 
th step, respectively.
Considering Equations (7.1) and (7.3), we have
Invoking the definition of 
, Equation (7.13) can be written as
To eliminate the tedious analytic computations of fractional derivatives of the virtual control law 
, the differentiator is employed to obtain the fractional derivatives of the virtual control law 
. According to Lemma 2.6, we have
where 
is a design positive constant.
Invoking Equation (7.15) and Lemma 2.6, we obtain
where 
is the estimation error of the differentiator. From Lemma 2.6, we know 
, with 
.
Considering Equations (7.14) and (7.16) yields
Furthermore, the virtual control law 
is designed as
where 
is a design constant.
Substituting Equation (7.18) into Equation (7.17) yields
From Equation (7.19) and Lemma 2.6, we have
According to Equation (7.3), we obtain
Considering the signals 
and 
, the Lyapunov function candidate is chosen as
On the basis of Lemma 2.1, the Caputo derivative of 
can be described as
Invoking Equations (7.20) (7.21), and (7.23), we have
where 
and 
will be handled in the next step.
Step 
Considering the system (7.1), the Caputo derivative of 
can be written as
On the basis of Lemma 2.4, a neural network is used to approximate the unknown nonlinear function 
; we obtain
Invoking Equation (7.3), we have
To eliminate tedious analytic computations of fractional derivatives of the virtual control law 
, the differentiator is employed to obtain the fractional derivatives of the virtual control law 
. According to Lemma 2.6, we obtain
where 
is the design positive constant.
Considering Equation (7.28) and Lemma 2.6, we obtain
where 
is the estimation error of the differentiator. From Lemma 2.6, we know 
with 
.
Combining Equations (7.27) and (7.29) yields
To compensate for the effect of the external disturbance 
, the SMFODO is designed to estimate it. To develop the SMFODO, the following auxiliary variable is defined as
and the intermedial variable 
is given by
where 
is a design constant, 
is the estimate of the unknown constant 
, and 
is the estimate of 
.
According to Equations (7.30) and (7.32), the Caputo derivative of Equation (7.31) yields
where 
.
Considering Assumption 7.3 and Equation (7.33), we have
where 
and 
.
The SMFODO is designed as
where 
is the estimate of the disturbance 
, and 
is a design constant of the SMFODO.
Invoking Equations (7.33) and (7.35), we obtain
where 
.
Consideration of Assumption 7.3 and the definition of 
yields
where 
and 
.
Define 
. Thus, we have
From Lemma 2.3 and Equation (7.38), we know that the disturbance estimation error 
is bounded when 
. Therefore, we can assume 
where 
is an unknown constant.
Furthermore, the controller 
is designed as
where 
is a design constant and 
is the estimate of the unknown constant 
.
Substituting Equation (7.39) into Equation (7.30) yields
From Equation (7.40), we have
According to Equation (7.3), we obtain
Considering the signals 
, 
, 
, 
, 
, 
, and 
, the function candidate is chosen as
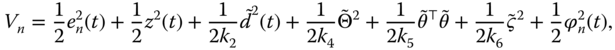
where 
, 
, and 
are design constants and 
.
On the basis of Lemma 2.1, the Caputo derivative of 
can be described as
Invoking Equations (7.34) (7.37) (7.41), and (7.42), Equation (7.44) can be written as
Consider the adaptive laws for 
, 
, and 
as follows:
Substituting Equations (7.46) (7.47), and (7.48) into Equation (7.45), and considering the following facts:
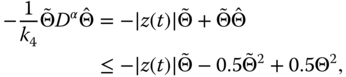
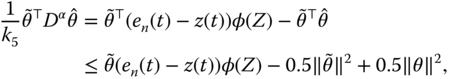
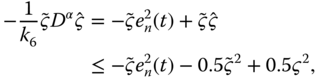
we have
This design procedure of the FODO-based adaptive neural control can be summarized in the following theorem, which contains the results of adaptive control for uncertain FOCS (7.1) in the presence of input saturation and external disturbance.
7.3 Simulation Examples
To illustrate the effectiveness of the proposed SMFODO-based adaptive neural control scheme for the uncertain FOCS with external disturbance and input saturation, the numerical simulations of two fractional-order chaotic systems will be studied.
7.3.1 Fractional-Order Chaotic Electronic Oscillator
Consider the following fractional-order chaotic electronic oscillator model [227]:
where 
, 
, and 
are system state variables, 
is a designed parameter, and the function 
satisfies
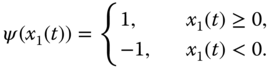
The fractional order is chosen as 
and the parameter is set as 
; the system (7.61) is a chaotic system based on the theory of Tavazoei and Haeri [228]. Furthermore, the chaotic behavior of Equation (7.61) is shown in Figure 7.1, for initial conditions of system (7.61) chosen as 
.
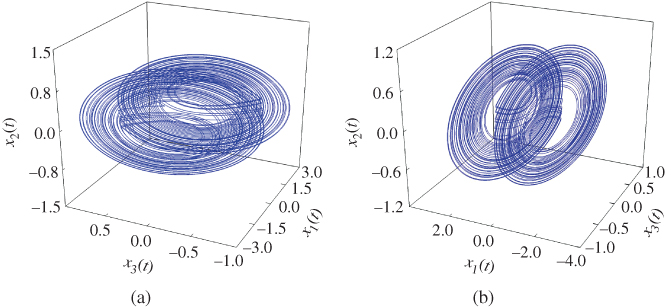
Figure 7.1 Chaotic behaviors of fractional-order chaotic electronic oscillator model (7.61): (a) 
–
–
space; (b) 
–
–
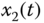space.
According to these simulation results, it can be seen that the system (7.61) is chaotic without control input. To facilitate the output signal 
of the system (7.61) to track the desired signal 
, the input control is considered in Equation (7.61). At the same time, the system uncertainty and the unknown external disturbance are also considered for the system (7.61).
From Equations (7.1) and (7.61), we have the following:
where 
, with 
, 
is the desired control input, 
is the unknown time-varying disturbance, and 
is the unknown nonlinear function.
Theorem 7.1 is applied to the uncertain fractional-order electronic oscillator model (7.63) to render the output signal 
to track the reference signal 
. In the simulation studies, for fractional order 
, the initial conditions are chosen as 
, 
, 
, 
, 
, 
, 
, 
, 
, and 
. The system parameters are selected as 
and 
. The control parameters are chosen as 
, 
, 
, 
, 
, 
, and 
. The uncertainty is assumed as 
. The external disturbance is assumed as 
. Furthermore, we define 
. On the basis of the result of Ishteva [225], we have 
, where 
denotes the square root of minus one and 
and 
are arbitrary numbers. Therefore, Assumptions 7.2 and 7.3 are satisfied.
Simulation results of the uncertain fractional-order electronic oscillator model (7.63) are shown in Figure 7.2, Figure 7.3, and Figure 7.4. Tracking results of the uncertain fractional-order electronic oscillator model with external disturbance and input saturation under the proposed adaptive neural control scheme are shown in Figure 7.2. According to Figure 7.2a, the tracking performance of the uncertain FOCS (7.63) is satisfactory. The tracking error 
between the output signal 
and the desired signal 
is bounded, as shown in Figure 7.2b. Furthermore, the observation performance of the proposed SMFODO (7.35) is presented in Figure 7.3. It is evident from Figure 7.3 that the disturbance observer could approximate the unknown external disturbance well. The control input signal, which is bounded, is shown in Figure 7.4. It is concluded from these simulation results that the proposed adaptive neural control scheme for uncertain fractional-order chaotic systems based on the SMFODO is effective.
Figure 7.2 Tracking control results of the fractional-order chaotic electronic oscillator (7.61) (a) Output 
follows desired trajectory 
; (b) tracking error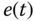 
.
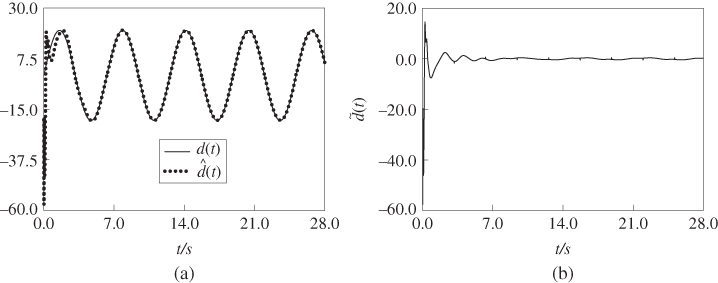
Figure 7.3 Disturbance estimation results of the fractional-order chaotic electronic oscillator (7.61) (a) Disturbance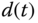 
and approximation output of 
; (b) observation error 
.
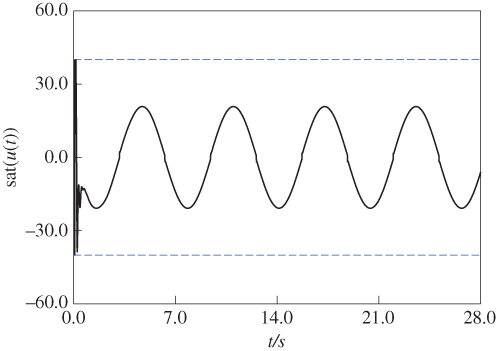
Figure 7.4 Control input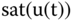 
of the fractional-order chaotic electronic oscillator (7.61).
7.3.2 Fractional-Order Modified Jerk System
The fractional-order modified jerk system is given as follows [229]:
where 
, 
, and 
are system state variables, and 
is a design parameter.
The fractional order is set as 
and the parameter is chosen as 
; the system (7.64) is a chaotic system based on the theory of Tavazoei and Haeri [228]. Furthermore, if the initial condition of the system (7.64) is chosen as 
, the chaotic behavior of the system (7.64) is given in Figure 7.5.
Figure 7.5 Chaotic behavior of (7.64): (a) 
–
plane; (b) 
–
plane; (c) 
–
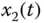plane; (d) 
–
–
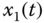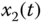space.
From these simulation results, it can be seen that the system (7.64) is chaotic without input control. To make the output signal 
of the system (7.64) track the desired signal 
, the input control is considered in Equation (7.64). Meanwhile, the unknown uncertainty and the unknown external disturbance are also considered in Equation (7.64). From Equations (7.1) and (7.64), we have the following:
where 
with 
, 
is the desired control input, 
is the unknown time-varying disturbance, and 
is the unknown nonlinear function.
According to Theorem 7.1, the output signal 
of the uncertain fractional-order modified Jerk system (7.65) is guaranteed to track the reference signal 
. To realize this simulation, the fractional order is chosen as 
, the initial conditions are chosen as 
, 
, 
, 
, 
, 
, 
, 
, 
, and 
. The system parameter is selected as 
. The control parameters are chosen as 
, 
, 
, 
, 
, 
, and 
. The uncertainty is assumed as 
. The external disturbance is assumed as 
. Furthermore, we define 
.
Simulation results are shown in Figure 7.6, Figure 7.7, and Figure 7.8 for the uncertain fractional-order modified Jerk system (7.65). According to the proposed adaptive neural control scheme, the tracking results are shown in Figure 7.6 for the uncertain fractional-order modified Jerk system with external disturbance and input saturation. From Figure 7.6, we note that satisfactory tracking performance is obtained. Figure 7.6b shows that the tracking error 
is bounded. In addition, the disturbance estimation performance of the proposed SMFODO (7.35) is shown in Figure 7.7. It is evident, based on Figure 7.7, that the disturbance observer could approximate the unknown external disturbance well. The bounded control input signal is shown in Figure 7.8. According to these simulation results, we can conclude that the proposed SMFODO-based adaptive neural control scheme is viable for uncertain fractional-order chaotic systems.
Figure 7.6 Tracking control results of the fractional-order modified jerk system (7.64) (a) Output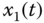 
follows desired trajectory 
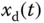; (b) tracking error 
.
Figure 7.7 Disturbance estimation results of the fractional-order modified jerk system (7.64) (a) Disturbance 
and approximation output of 
; (b) observation error 
.
Figure 7.8 Control input 
of the fractional-order modified jerk system (7.64).
7.4 Conclusion
An adaptive neural tracking control scheme has been proposed for a class of uncertain fractional-order chaotic systems subjected to unknown disturbance and input saturation in this chapter. An auxiliary design system has been used to compensate for the effect of the input saturation. At the same time, an SMFODO has been designed to guarantee the convergence of the disturbance estimation error. On the basis of the radial basis function neural network, the auxiliary system, and the SMFODO, an adaptive neural control scheme has been presented for fractional-order chaotic systems with unknown disturbance and input saturation. Under the integrated effect of unknown external disturbance and unknown uncertainty, the bounded convergence of all closed-loop signals has been guaranteed. Numerical simulation results have been given to show the effectiveness of the developed control scheme.