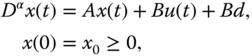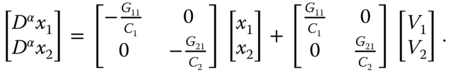Chapter 8
Stabilization Control of Continuous-Time Fractional Positive Systems Based on Disturbance Observer
8.1 Problem Statement
8.1.1 Notation and Definitions
denotes the 
-dimensional real space.
denotes the transpose of a matrix 
.- A matrix
is called a Metzler matrix if its off-diagonal elements are non-negative. - A matrix
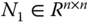can be seen as a non-negative matrix if all its elements are non-negative, e.g., 
. - A vector
can be seen as a non-negative vector if all its elements are non-negative, e.g., 
. It is said to be positive if all its components are positive (
). Furthermore, it is said to be negative if all its components are negative (
).
8.1.2 Preliminaries
Based on the Caputo definition of the fractional derivative, we consider the continuous-time fractional-order system with unknown non-negative constant disturbance as follows:
where 
and 
are constant matrices, 
is a state vector, 
is a control input vector, 
is an unknown non-negative constant disturbance vector, 
is an initial condition vector, and 
. This chapter aims to develop a sufficient condition based on the state feedback control method and a FODO to ensure that:
- 1. The fractional-order system (8.1) is positive.
- 2. The fractional-order system is asymptotically stable, that is,
.
To obtain these conclusions, the following assumptions, definitions and lemmas are required.
According to Definition 8.1, the following results are given.
8.2 Main Results
In this section, a FODO is introduced to estimate the external unknown non-negative constant disturbance of a continuous-time fractional-order linear system (8.1). Furthermore, the stability of the closed-loop fractional positive system is investigated, based on a FODO.
8.2.1 Fractional Disturbance Observer
According to the integer-order disturbance observer design technique presented in Chen et al. [105], the FODO will be introduced for the fractional-order system (8.1) in this section. On the basis of the property of the Caputo definition, we obtain that the Caputo derivative of a constant is zero. Thus, for a constant disturbance, we have
where 
denotes a zero vector.
From the system (8.1), 
can be written as
The FODO is described as
where 
is a design matrix of the FODO (8.18). The disturbance estimation error is defined as
According to Equations (8.16) (8.17) (8.18), and (8.19), we obtain
if the design matrix 
is chosen such that the disturbance estimation error system
tends to stability. Then the disturbance estimate output 
can approximate to 
, if 
.
Since 
is not available, the FODO (8.18) cannot be realized. To handle the aforementioned issue, an auxiliary design system is defined as
Considering Equations (8.18) and (8.22), we have
From Equation (8.22), the disturbance estimate output 
can be written as
The designed FODO consists of Equations (8.23) and (8.24). Invoking Equations (8.19) (8.23), and (8.24), the disturbance estimation error is given by
where 
.
From Equation (8.25), we know that the disturbance estimate output 
can approximate the disturbance 
well if the matrix 
satisfies 
, 
. Thus, 
is asymptotically stable based on Lemma 8.4.
According to this analysis, we know that the disturbance estimation error 
is upper bounded.
To ensure that the closed-loop system is positive and asymptotically stable, the initial conditions must satisfy 
and 
for the fractional-order system (8.1). Thus, to guarantee the initial value 
of the disturbance estimation error, the following theorem is given.
8.2.2 Stabilization Control of Fractional Positive System
Consider the continuous-time fractional-order system given as Equation (8.1). Using the state-feedback control method and the designed disturbance observer (8.23 and 8.24), the desired control input is designed as
where 
is a design matrix. On the basis of Equations (8.1) (8.23) (8.24), and (8.30), the closed-loop control system is illustrated in Figure 8.1. Substituting Equation (8.30) into Equation (8.1), we obtain
To analyze the stability of the closed-loop system (8.31), an augmented system based on Equations (8.25) and (8.31) is given as follows:
On the basis of Equation (8.32), we have
where
and 
denotes a zero matrix.
Figure 8.1 Whole closed-loop control system.
Furthermore, the following theorem is given based on Lemma 8.7 for the fractional-order system (8.33).
8.2.3 Simulation of Fractional Positive System
Considering a continuous-time fractional-order linear system with unknown constant disturbance described by Equation (8.1), the following system matrices 
and 
are given as
This section aims at designing a controller 
to render the closed-loop system states non-negative and asymptotically stable. Thus, the conditions in Theorem 8.2 must be satisfied. According to the linear programming method, the control gain matrices 
and 
are obtained as
For the augmented system (8.33), we have
From Equation (8.41), the eigenvalues of 
are given as 
, 
, 
, and 
. Thus, the eigenvalues of 
are located in the left half of the complex plane. Then the augmented system (8.33) is asymptotically stable. Furthermore, we obtain that 
is a Metzler matrix. Therefore, the augmented system (8.33) is positive for any initial condition 
. From this analysis, we conclude that the augmented system (8.33) is positive and asymptotically stable under conditions (8.40) and (8.41).
For the numerical simulation, we choose the fractional order as 
; the constant disturbances are assumed as 
. The initial conditions are chosen as 
, 
, 
, and 
. Then we obtain that 
and 
. On the basis of the numerical simulation method for fractional-order systems [164], the estimation performance of the FODO (8.23) and (8.24) is shown in Figure 8.2, which shows that good estimation performance is achieved. In addition, if we use Equations (8.3) and (8.4) to realize the numerical simulation of the augmented system (8.33), the ML function will converge slowly for the case of the large variable.
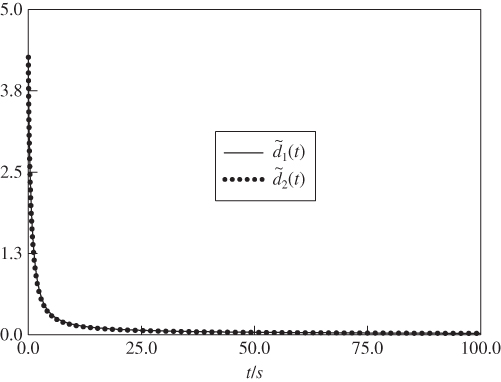
Figure 8.2 Disturbance estimation errors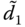 
and 
for the simulation of fractional-order system (8.1) and (8.39).
Using the same numerical simulation method, the simulation results of augmented system (8.33) are presented in Figure 8.3. From Figure 8.3, the state variables 
and 
are positive and asymptotically stable. According to these simulation results, we conclude that the FODO (8.23) and (8.24) is effective for constant disturbances, and that the designed controller 
can guarantee that the closed-loop system states are non-negative and asymptotically stable. Furthermore, the simulation results are shown in Figure 8.4 for the case of the closed-loop control system without FODO. From Figure 8.4, the state variables 
and 
are not be controlled to zero. However, the state variables 
and 
are controlled to zero for the case of the closed-loop control system with FODO based on Figure 8.3. Thus, the developed FODO-based control scheme can improve the performance of the closed-loop control system.
Figure 8.3 Responses of state variables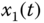 
and 
for the fractional-order system (8.1) and (8.39) with FODO.
Figure 8.4 Responses of state variables 
and 
for the fractional-order system (8.1) and (8.39) without FODO.
8.2.4 Stabilization Control of Fractional Bounded Positive System
In this section, a sufficient condition is given to guarantee that a closed-loop fractional bounded positive system is asymptotically stable. Invoking the system (8.1), the following continuous-time fractional-order system with disturbance is described by the following:
where 
is the bound of 
.
Combining Equations (8.33) and (8.42), we obtain
where 
is the bound of 
. We define 
, 
, and 
, with 
.
Considering Theorem 8.2 and the system (8.43), we have the following theorem.
According to Theorem 8.3, we can conclude that 
. Since 
, we have that 
for any initial condition 
. Therefore, the state variables of the closed-loop fractional-order system (8.43) are bounded, and the system (8.43) is positive and asymptotically stable for any initial condition 
.
8.2.5 Simulation of Fractional Bounded Positive System
In this section, a fractional electrical circuit [162] is employed to illustrate the effectiveness of the proposed control scheme. The fractional electrical circuit is shown in Figure 8.5, where 
and 
are capacitor voltages, 
and 
are source voltages, 
and 
are node voltages, 
and 
are ultracapacitors with fractional order 
, and 
, 
, 
, 
, and 
are conductances. According to Figure 8.5, we have
Furthermore, we obtain
From Equation (8.47), this yields
According to Equation (8.46), one gets
Combining Equations (8.48) and (8.49), we have
where
Figure 8.5 Fractional electrical circuit.
According to this analysis, the fractional-order circuit always has perfect status. However, in the real world, many uncertain factors exist in circuits, such as consumption of internal resistance and wires, and so on. Thus, the disturbance is considered in Equation (8.50); it can be written as
Without loss of generality, to simplify the notation, we choose the values of 
, 
, 
, 
, 
, 
, 
, and 
as 
, 
, 
, 
, 
, 
, 
, and 
. Thus, the system matrices 
and 
are described as follows:
According to the state feedback control method, a controller 
is designed to stabilize the fractional-order system, so that the closed-loop system is non-negative and asymptotically stable. Therefore, the conditions in Theorem 8.3 must be satisfied. Based on the linear programming method, we obtain the control gain matrices 
and 
as follows:
Furthermore, the bound of 
is given by
On the basis of the augmented system (8.43), we obtain
According to Equation (8.55), the eigenvalues of 
are given by 
, 
, 
, and 
. Therefore, the eigenvalues of 
are located in the left half of the complex plane. Then we obtain that the augmented system (8.43) is asymptotically stable. In addition, we obtain that 
is a Metzler matrix. Thus, for the initial condition 
, the augmented system (8.43) will be positive. On the basis of this analysis, we obtain that the augmented system (8.43) is positive and asymptotically stable based on the conditions (8.53) and (8.55).
In this numerical simulation, the fractional order is chosen as 
, and the constant disturbances are assumed as 
. Furthermore, we choose the initial conditions 
, 
, 
, and 
. Then, 
and 
are obtained. According to the numerical simulation method for fractional-order systems [164], Figure 8.6 shows the estimation performance of the FODO (8.23) and (8.24). It can be seen that good estimation performance is realized. For the numerical simulation of Equation (8.43), the simulation results are presented in Figure 8.7. From Figure 8.7, the state variables 
and 
are bounded, positive, and asymptotically stable. From these simulation results, we conclude that the FODO (8.23) and (8.24) is effective for constant disturbances, and the designed controller 
can guarantee that the closed-loop system states are positive and asymptotically stable.
Figure 8.6 Disturbance estimation errors 
and 
for the simulation of the fractional electrical circuit (8.46).
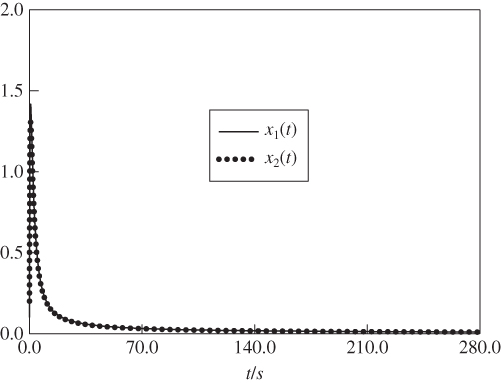
Figure 8.7 Responses of state variables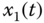 
and 
for the fractional electrical circuit (8.46) with FODO.
Conversely, the simulation results of the closed-loop control system without FODO are given in Figure 8.8. According to Figure 8.8, we know that the state variables 
and 
cannot be controlled to zero. However, the state variables 
and 
can converge to zero when the FODO is considered in the closed-loop control system, as shown in Figure 8.8. As a result, the developed disturbance estimation technique can reject the effect of external disturbances. Therefore, the performance of the closed-loop system can be improved by the developed control scheme.
Figure 8.8 Responses of state variables 
and 
for the fractional electrical circuit (8.46) without FODO.
8.3 Conclusion
In this chapter, the FODO-based stabilization control scheme has been studied for a continuous-time fractional-order linear positive system in the presence of unknown constant disturbance. To improve the disturbance attenuation, a FODO has been employed to approximate the unknown disturbances. By using the developed FODO and the state feedback control method, a stabilization controller has been designed to guarantee that the closed-loop system states are positive and asymptotically stable. Furthermore, a sufficient condition of stabilization has been given for the case of constrained states of fractional-order positive systems with constant disturbances. At the same time, two numerical simulations have been shown to illustrate the effectiveness of the developed control scheme.