The Quest for God's Number
RIK VAN GROL
The Rubik's cube triggered one of the largest puzzle crazes in the world. The small mechanical puzzle, invented by Erno' Rubik in Hungary, has sold more than 350 million copies. Although it has existed since 1974, the popularity of the cube skyrocketed around 1980, when the cube was introduced outside of Hungary. In the early days, simply solving the puzzle was the main issue, especially because no solution books were available and there was no Internet. But solving the puzzle in the shortest amount of time was also hot news. In the early 1980s the best times were on the order of 24 seconds.
By the end of the 1980s, the craze was starting to ebb, but in certain groups the puzzle remained very much alive, and now the Rubik's cube is making a comeback. Solving the cube the quickest—speed cubing—is currently a major activity. The fastest times are under 8 seconds with the average around 11 seconds. The foundation for a fast solving time is a good algorithm, and so the search for efficient algorithms has been an important area of study since the early 1980s. The ultimate goal is to discover the best method of all—the optimal solution algorithm— which has been dubbed God's algorithm.
God's algorithm is the procedure to bring back Rubik's Cube from any random position to its solved state in the minimum number of steps.
The maximum of all minimally needed number of steps is referred to as God's number. This number can be defined in several ways. The most common is in terms of the number of face turns required, but it can also be measured as the number of quarter turns. Whereas a quarter turn is either a positive or negative 90° turn, a face turn can be either of these or a 180° turn. A 180° face turn is equal to two quarter turns. Earlier this year, after decades of gradual progress, it was determined that God's number is 20 face turns. Thus, if God's algorithm were used to solve the cube, no starting position would ever require more than 20 face turns.
Apart from determining God's number, another major question has been to find out whether God's algorithm is an elegant sequence of moves that can be “easily” memorized, or if, instead, God's algorithm amounts to a short procedure with giant lookup tables. If it's the latter case, then no one will ever be able to learn how to solve the Rubik's cube in the minimal number of moves (read on to learn why this is true). Still, even if God's algorithm has no practical purpose, it is interesting to know what God's number is.
Playing God (with Small Numbers)
If you start with a solved cube and ask someone to make a few turns, you will (after some practice) be able to return it to the solved state in a minimum number of moves as long as the initial number of scrambling moves is not too large. With fewer than four scrambling moves, it is easy; with four, it becomes tricky. With five, it is simply hard. Some experts can handle six or even seven scrambling moves, but any more and it is essentially impossible to solve the cube in the minimal number of moves.
Generally speaking, most algorithms take between 50 and 100 moves. What if you were to randomly turn the cube 1,000 times? Will it take 1,000 moves to get it back? No, it still takes most algorithms 50 to 100 moves because the algorithms are designed to work from any starting position.
Starting Small:The 2 × 2 × 2 Cube
Unlike the classic 3 × 3 × 3 Rubik's Cube, the 2 × 2 × 2 cube has been completely analyzed. God's number is 11 in face turns and 14 in quarter turns. To find these values, all possible configurations of the 2 × 2 × 2 cube were cataloged, and for each of these configurations, the minimal number of turns needed to reach the solved state was determined. This brute force approach was possible because there are “only” about 3.7 million configurations to study.
To calculate the number of configurations for the 2 × 2 × 2 cube, we start with the observation that the eight corner cubies (as they are called) can be permuted in 8! ways. For any such permutation, each corner cubie can be oriented in three ways, leading to 38 possible orientations. However, given the orientation of seven corners, the orientation of the eighth is determined by the puzzle mechanism, so the corners really have 37 orientations. As the orientation of the whole cube is not fixed in space (any one of the eight corners can be placed in, say, the top-front-right position, and once it is placed there, the entire cube can be rotated so that any one of three faces is on top), the total number of permutations needs to be divided by 8 × 3 = 24. Hence, the total number of positions is
![]()
There are only 2,644 positions for which 11 face turns are required to solve the puzzle. Assuming all configurations have the same likelihood of being a starting position, the average number of face turns required to solve the puzzle is 9. Likewise, there are only 276 positions from which 14 quarter turns are required, and on average, 11 quarter turns are required to solve the puzzle.
A Leap in Complexity: The 3 × 3 × 3 Cube
Until recently, God's number for the 3 × 3 × 3 cube was not known. From the late 1970s until now the search area has been limited by two numbers: the lower bound and the upper bound. The lower bound Glow is determined by proving that there are positions that require at least Glow turns. The upper bound Ghigh is determined by proving that no position requires more than Ghigh turns.
So, how many configurations are there? With 8 corner cubies and 12 edge cubies, there are 8! × 12! × 38 × 212 different patterns, but not all patterns are possible:
• With 8 corners there are 8! corner permutations, and with 12 edges there are 12! edge permutations. However, because it is impossible to interchange two edge cubies without also interchanging 2 corner cubies, the total number of permutations should be divided by 2.
• Turning of corner cubies (keeping their position, but cycling the colors on their three faces) needs to be done in pairs only 7 corner cubies can be turned freely.
• Flipping of edge cubies (keeping their position, but switching the colors of their two faces) needs to be done in pairs—only 11 edge cubies can be flipped freely.
Because of the six center pieces, the orientation of the cube is fixed in space, so the number of permutations should not be divided by 24 as with the 2 × 2 × 2 cube. Hence, the number of positions of the 3 × 3 × 3 cube is
![]()
This is astronomically bigger than 3,674,160 for the 2 × 2 × 2 cube, and it made searching the entire space computationally impossible. For instance, if every one of the 350 million cubes ever sold were put in a new position every second, it would take more than 3,900 years for them to collectively hit every possible position (with no pair of cubes ever sharing a common configuration). Or to put it another way: if a computer were capable of determining the fewest number of moves required to solve the cube for 1,000 different starting positions each second, it would take more than a billion years of computing time to get through every configuration.
Determining God's number by independently improving the upper and lower bounds was a quest that lasted for three decades—but it has finally come to an end. In July 2010 the upper and lower bounds met at the number 20.
Raising the Lower Bound
Using counting arguments, it can be shown that there exist positions requiring at least 18 moves to solve. To see this, one counts the number of distinct positions achievable from the solved state using at most 17 moves. It turns out that this number is smaller than 4.3 × 1019. This simple argument was made in the late 1970s (see Singmaster's book in the Further Reading section), and the result was not improved upon for many years. Note that this is not a constructive proof; it does not specify a concrete position that requires 18 moves. At some point, it was suggested that the so-called superflip would be such a position. The su- perflip is a state of the cube where all the cubies are in their correct position with the corner cubies oriented correctly, but where each edge cubie is flipped (oriented the wrong way).
It took until 1992 for a solution for the superflip with 20 face turns to be found, by Dik Winter. In 1995 Michael Reid proved that this solution was minimal, and thus a new lower bound for God's number was found. Also in 1995, a solution for the superflip in 24 quarter turns was found by Michael Reid, and it was later proved to be minimal by Jerry Bryan. In 1998 Michael Reid found a new position requiring more than 24 quarter turns to solve. The position, which he calls the superflip composed with four spots, requires 26 quarter turns. This put the lower bound at 20 face turns or 26 quarter turns.
Lowering the Upper Bound
Finding an upper bound requires a different kind of reasoning. Perhaps the first concrete value for an upper bound was the 277 moves mentioned by David Singmaster in early 1979. He simply counted the maximum number of moves required by his cube-solving algorithm. Later, Singmaster reported that Elwyn Berlekamp, John Conway, and Richard Guy had come up with a different algorithm that took at most 160 moves. Soon after, Conway's Cambridge Cubists reported that the cube could be restored in at most 94 moves. Again, this reflected the maximum number of moves required by a specific algorithm.
A significant breakthrough was made by Morwen Thistlethwaite. Whereas algorithms up to that point attacked the problem by putting various cubies in place and performing subsequent moves that left them in place, he approached the problem by gradually restricting the types of moves that could be executed. Understanding this method requires a brief introduction to the cube group.
As we work with the cube, let's agree to keep the overall orientation of the cube fixed in space. This means that the center cubies on each face will never change. We may then label the faces Left, Right, Front, Back, Up, and Down. The cube group is composed of all possible combinations of successive face turns, where two such combinations are equal if and only if they result in the same cube configuration. We denote the clockwise quarter turns of the faces by L, R, F, B, U, and D, and use concatenation as the group operation. For instance, the product FR denotes a quarter turn of the front face followed by a quarter turn of the right face, while F2 denotes a half turn of the front face. The group identity, I, is no move at all. So, for example, F4 = I.
Thistlethwaite divided the cube group G0 into the following nested chain of subgroups:
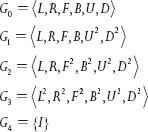
Thistlethwaite's algorithm works by first performing a few moves that result in a configuration that no longer requires quarter turns of the U and D faces (although it still requires half turns). From this point on, only moves in the subgroup Gt are needed. A few additional Gt moves puts the cube into a position where quarter turns are no longer needed for the F and B faces, and so on. The algorithm uses large lookup tables at each step, and while it is not practical for humans, the successive sets of moves per subgroup are small enough to allow computer analysis. Initially, Thistlethwaite showed that any configuration could be solved in at most 85 moves. In January 1980 he improved his strategy to yield a maximum of 80 moves. Later that same year, he reduced the number to 63, and then again to 52.
After this rush of activity, progress stalled for several years. In 1989 Hans Kloosterman reported an algorithm that required at most 44 moves, which he later improved to 42. In 1992 Herbert Kociemba improved Thistlethwaite's algorithm by reducing it to a two-phase algorithm requiring only the subgroups G0, G2, and G4. Using Kociemba's ideas, Michael Reid announced in 1995 that he had improved the upper bound to 29 face turns.
At about this time, Richard Korf introduced a new approach. Instead of using a fixed algorithm, his strategy simultaneously searched for a solution along three different lines of attack. On average, his algorithm appeared to solve the cube in 18 moves. There was, however, no worst- case analysis, and so the upper bound held still at 29.
Things turned quiet again until 2006, when Silviu Radu initiated a new countdown by reducing the upper bound to 27. The next year, Gene Cooperman brought it down to 26. With the lower bound of 20 face turns in sight, Tomas Rokicki entered the picture, reducing the upper bound to 25 in March 2008. Working with John Welborn, he had it down to 24 by April, then 23 in May, and 22 by August. Finally in July 2010, Rokicki announced an upper bound of 20, the established value of the lower bound and therefore the long-sought-after value of God's number.
Rokicki worked with Kociemba, as well as mathematician Morley Davidson and Google engineer John Dethridge. The team used symmetry arguments to significantly reduce the search space and then managed to partition the space of all configurations that remained into pieces small enough to fit onto a modern computer. They then made use of the enormous computing resources available through Google. Had the entire problem been done on a single good desktop PC, they report it would have taken about 35 years to complete, but by farming out different pieces to a large number of computers, the team was able to complete the calculation in just a few weeks.
It is a remarkable achievement.
Epilogue
Now that the quest for God's number for the classic 3 × 3 × 3 cube has come to an end, it is time to look ahead. Is there an elegant version of God's algorithm—one that a human could implement? And what is God's number for the 4 × 4 × 4, 5 × 5 × 5,6 × 6 × 6, and 7 × 7 × 7 cubes, all of which are now on the market? Finding God's number for such puzzles is a challenge that should last far into the future. The number of positions for the 7 × 7 × 7 cube reaches 2.0 × 10160.
Further Reading
Two influential early books are David Singmaster's Notes on Rubik's Magic Cube (Enslow Publishers, 1981), which is readable and has many technical details; and Patrick Bossert's You Can Do the Cube (Puffin Books, 1981), a how-to guide written when the author was 12 years old that sold more than 1.5 million copies. Another classic, complete with the requisite group theory, is Inside Rubik's Cube and Beyond, by Christoph Bandelow (Birkhauser, 1982). On the web, an excellent how-to guide with several links to other sources can be found at Jaap's Puzzle Page: http://www.jaapsch.net/puzzles/. A brief history of the quest for God's number can be found on Tom Rokicki's site, http://www.cube20.org.
