Celebrating Mathematics in Stone and Bronze
HELAMAN FERGUSON AND CLAIRE FERGUSON
Motives
I celebrate mathematics with sculpture and sculpture with mathematics. Eons-old stone strikes me as a perfect medium through which to celebrate timeless mathematics.
I used to simplify life by putting science in one room and art in another. This avoided exposing my entangled soul, lest someone think me not sufficiently dedicated to one discipline or the other. Keep science and art separated, my generation was informed. “You can't do both.” Parents advised, “If you can do science and have a lick of sense, you'd better. Artists starve.”
Now we live in a golden age of both art and science. More career choices. I am grateful that I have had the opportunity to combine and do both [22].
Mathematicians have their own aesthetic, a sense of beauty and elegance difficult to communicate [2]. My design process starts with some inspiring mathematics. My sculpture convolves mathematical abstractions and fundamental forms shared by everybody.
Humans are toroidal. This feature links our anatomy and abstract topology. For example, the abstract mathematical idea could be a quotient space. An easy example is a torus. The shared form could be a handshake, a less easy example of a triply punctured torus. My convolution includes geometry, topology, and humanity in forms I can express in paper, computer, clay, bronze, and stone.
I design sculpture to be touchable. Art museum curators warn us to “Look, don't touch.” My sculpture succeeds when touched, held, fingered, crawled through, and then thought about.
Although I do not make models, I do make the invisible visible, touchable, and occasionally knowable. Each of my sculptures involves a circle of beautiful mathematical theorems. I love mathematics for reasons difficult for me to articulate in words, but which I can articulate in sculpture. I want some wonders of our beautiful art and science to have a life in a larger world [4].
Theorems in Bronze
LOST-WAX BRONZE
Like most sculptors, early on I cast my own bronzes. This process involves complex steps of positive primary, negative mold, positive wax, negative ceramic, and positive bronze. These precede chasing, patina, or polish of the final surface. Some pieces I cast solid, then carved, and then polished [4].
Bronze is very like cast iron and usually comes in ingots. Many industrial copper alloys go by the name of bronze, and bronzes throughout the world can differ in many respects. Manganese bronze is typically found in faucets. Fine art bronze in North America is an alloy of copper with silicon specialized for pour consistency and polishability. A typical “molecule” of silicon bronze is
9438Cu + 430Si + 126Mn + 4Fe + Zn + Pb.
Division of the coefficients of this “molecule” by 10,000 gives a parti- tion-of-unity recipe for fine art silicon bronze. Bronze has had industrial and military value through the ages; bronze artifacts have always been vulnerable, because we humans dream of peace but engage in war. Nonetheless, polished bronze collects light like no other medium, and it makes dazzling awards, e.g., [11, 14, 18, 19, 20].
UMBILIC TORUS NC
Some twenty years ago, I created Umbilic Torus NC in an elegant faience antique verde bronze [4].
I had already carved in stone a number of these twisted tori, for example, the umbilic toroid in a polishable Deseret limestone I pulled out of the Rocky Mountains. The NC refers to numerical control, at a time when milling machines were served by paper tape.
Figure 1. Umbilic toroid in Deseret limestone. Reprinted by permission of Claire and Helaman Ferguson.
The Umbilic Torus NC form intrigues me most among all twisted to- roids because of its explicit connection with the representation theory of GL (2, R), the 2 X 2 invertible real matrices. This group acts on homogeneous binary quadratic forms (two variables, three coefficients) to give the familiar stratification of ellipses, hyperbolas, and parabolas. This group also acts on homogeneous binary cubic forms (two variables, four coefficients) to give the stratification by elliptic umbilics, hyperbolic umbilics, parabolic umbilics, and pure cubics [5].
I wanted to carve the 1 / 3 twisted torus with radial cross-section deltoid (hypocycloid with three cusps) and sagittal cross-section cardioid (epicycloid with one cusp) with some numerical accuracy. I also wanted to articulate the surface with a surface-filling Peano-Hilbert curve. The three- axis milling machine presented a rapidly rotating carbide ball cutter to the material and received its point-to-point movements from paper tape. I solved the tool-path problem by discovering that the choice of a surface- filling curve for the tool path was more efficient and more aesthetic. The offsets and tool moves all had to be preprogrammed. At the time all this data in the G-code of the milling machine would generate enough paper tape to fill the manufacturing lab. Fortunately, the lab people found a hard disk drive to interface with the milling machine in lieu of the paper tapes.
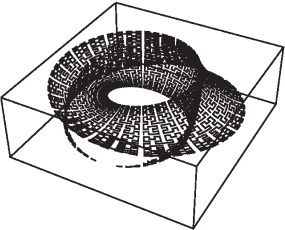
Figure 2. Umbilic Torus NC. Reprinted by permission of Claire and Helaman Ferguson.
In Figure 2 we see the tool path curve in three-space as a ghost trajectory of the path for the physical cutter to follow. This machine carving only gives the first primary positive curvilinear waffle form cut into a dense styrofoam. To create the primary form for the Umbilic Torus NC, I used applied mathematics, computer science, and engineering. After the many positive-negative steps of the lost-wax bronze casting process I finished the Umbilic Tori NC with antique verde patinas.
The umbilic torus image and others like it have appeared on the covers of calculus books. I encounter students who tell me they have spent a lot of time looking at those covers and the description of the image. One young woman told me she thought her calculus instructor awful and that the umbilic torus image and its description were what got her through the class.
Theorems in Stone
ON CARVING STONE
Stone is one of my favorite media. Maybe I choose stone because I was raised by a stone mason who saw beauty in common field stones. My aesthetic choices include geological age, provenance, and subtraction. We learn addition and then we learn subtraction. Subtraction is harder, isn't it?
Traditionally, one originates sculptures by either addition or subtraction. Addition is popular: model clay, add clay to an armature, or weld pieces of metal together. These are operations with modules. Most art schools do not teach subtraction in the form of carving stone. To begin with a block of stone and take away what is not desired, to leave the desired, is considered really old-fashioned. It is difficult to do and even more difficult to teach. But I think subtraction is more interesting than addition, especially if I subtract from stone myself.
Mathematicians are notorious for wanting to do things themselves, prove their own theorems, or prove other people's theorems without looking at the known proofs. Sculptors tend to the opposite. Most stone carving today is like a glamorous rock-music recording production; artists with enough money job it out—outsource. The question for me is “job out what?” How do I job out C ™ functions? Negative Gaussian curvature? More important, having done so, what have I learned?
But there may be no practical reason to outsource simply because we live in amazing times. I can go almost anywhere and put together a modest stone carving studio from the inventory of a local hardware store, complete with diamond saws. That would have been impossible when I began pulling my own studio together some forty years ago. Most of the credit for this goes to the recent development of diamond-cutting technology [8]. Because of synthetic diamond production, sawn and polished stone can be found everywhere now, while even a short time ago it was prohibitively expensive.
Usually my sculpture goes into colleges or universities. I can expect my work to be there for generations of faculty, colleagues, students, employees, and their families to enjoy. My work may well perturb their preconceptions about why creative math and creative art possess the unique and inspiring vitality that they do possess.
If a stone has been around for millions of years, it will probably last another few thousand years, especially after I carve it into something of no obvious military or industrial value. I start with a relatively worthless piece of stone, and when I get done with it, from a functional point of view, it is even more worthless. This suits me because my stone sculpture will probably last longer as a result.
If someone digs up my theorems in stone in a few thousand years, I expect that the excavator can decode what I have encoded and continue celebrating mathematics. I'd like my sculpture to be big and strong enough for a few beautiful mathematical theorems to survive outside of books, classrooms, and the here and now, e.g., [9, 10, 12, 13, 16, 17] .
Figure 3. Reprinted by permission of Claire and Helaman Ferguson.
Next I give a mathematical discussion of subtraction and relate that to a block of stone. Then I conclude with a discussion of two of my large stone sculptures.
SUBTRACTION
One of our oldest mathematical algorithms is the Euclidean algorithm as found in Euclid's Book VII for pairs of integers and Book XI for pairs of real numbers. The algorithm is described in Euclid as continually subtracting in turn. In 1977 Rodney Forcade and I discovered, with proofs, uncountably many generalizations of Euclid's algorithm to n- tuples of reals, complexes, or quaternions [6]. Now known as PSLQ, these are subtraction algorithms. I begin with a list of real numbers x ∈ 
and construct a list of integers m ∈ 
, relating them in a linear combination, x · m = 0, if such a relation m exists. If no such relation is constructed, then at least PSLQ constructs a lower bound on the size of any possible relation. PSLQ will discover an underlying relation of dimension n in time that is a polynomial function in n and the logarithm of the Euclidean norm of the coefficients; I consider our algorithm a subtraction process with GL(n, 
) matrix inverse operations. This subtraction algorithm has led to many new discoveries [1].
I give an example of one of these discoveries: a new formula for p was discovered with PSLQ [3]. This formula has the remarkable feature that permits binary digits of ? beginning at some arbitrary position to be computed directly, without any need to compute any of the preceding digits.
Figure 3 looks like subtraction: the large positive black area is a disk with three smaller disks subtracted so that the figure has area ?. This partially deleted disk is reasonably accurate as printed here, like the one I cut from black acrylic to 1,000th of an inch with a Cartesian laser robot.
The area π of this disk is given by an inner product of a real vector x = (x1, x4, x5, x6) ∈ R4 and an integer lattice point m = (4, –2,–1, –1) ∈ Z4. The three negatives correspond to the three deleted disks. In the theorem,
π = x · m,
where
we only need j = 1, 4, 5, 6 to express π. These xj are real numbers, given by the geometrically convergent series above; we can compute them to arbitrary precision.
The discovery of this new π formula [3] was made by taking the input for PSLQ to be
Let a basis for 
be given by 9 × 9 rank 8 matrix H, so that yH = 0. Then PSLQ iterates on the pair y, H presented as sufficiently long decimal strings. Each iteration constructs an integer matrix A ∈ GL(9, ), where A-1H becomes small. In the process yA becomes small, too, but more important, a coordinate of yA may become 0 so that a column of A is a relation fory.
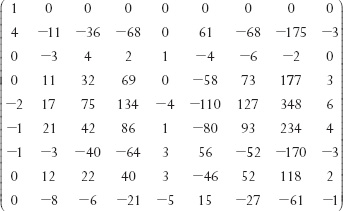
For this example, taking 32-place decimal presentations ofy and H, after 50 iterations PSLQ constructed the GL(9, ) matrix A = which has determinant ± 1. The first column of this 9 × 9 matrix A is a relation for y, a fairly small lattice point. The rows of the inverse matrix A–1 actually give good rational approximations to the vector y ∈ 
9. Note that some of the coordinates of this first column of A are 0. Hence the formula for π needs only four of the xj's.
Where is the block of stone in all this? The block is in nine dimensions and is very tiny. In this example the block has volume on the order of 10–288.
The vector y ∈ 9 is presented for this experiment by thirty-two decimals in each of the nine coordinates, not as real numbers. In any computer we know of, all the arithmetic is in terms of truncated rational numbers, bit strings most likely. The PSLQ experiment does all these subtractions and in the end only reveals that in this tiny block there is a real vector with that relation. That is the discovery, and it is as empirical as carving stone.
PSLQ gives no proof. The proof, as for all the discoveries made by PSLQ, must be found elsewhere. Of course, the form once discovered may suggest a proof. Once we see this formula for π we can easily imagine that it could have been discovered by Newton or Euler, but evidently it was not. There are many more PSLQ discoveries than we have proofs for at this time, and I suppose that is as it should be.
FIBONACCI FOUNTAIN, ESSENTIAL SINGULARITY II
A rainbow occasionally appears in my Fibonacci Fountain. I completed this sculpture, quite coincidentally, eight centuries after Leonardo of Pisa introduced addition and subtraction with Arabic numerals on paper instead of operating with Roman numerals or an abacus (it should be noted that decimal positional arithmetic was discovered in India at least seven centuries before Leonardo and was later developed by the Arabs). We remember him for giving us that rabbit problem, leading to the Fibonacci numbers:
0,1,1,2,3,5,8,13,21,34,55,…,
from which descended linearly recurrent sequences [21]. It would seem that linear recurrent sequences are even more ubiquitous than rabbits.
As I walk about the 2/3-mile circumference of the 15/2-acre Lake Fibonacci at the Maryland Science and Technology Center in Bowie, Maryland, I see an amazing assortment of plants and trees. The area is a shrunken plantation; only 500 acres remain. If I nose about a bit, I observe Fibonacci phyllotaxis in scale, seed, cone, sprout, leaf, and twig of these ratios (where the subscript denotes the relevant ratio): elm1/2, balsam2/3, oak2/5, cherry2/5, hemlock3/8, poplar3/8, pear3/8, pine5/8, willow5/13, daisy8/13, sunflower34/55. The plantation owners collected and planted every sort of flower, bush, and tree available over at least two centuries. The collection is now neglected, and the collectors and their slaves lie buried on a forested hill near the Fibonacci Fountain.
My Fibonacci Fountain contains over 45 tons of billion-year-old Texas granite. It stands 18 feet above the water, supported underwater by concrete and steel to a depth of 14 feet, which is supported in turn by 28 pilings in 40 feet of mud. When the test cores were drilled no bedrock was found.
Fourteen water cannons spurt a mathematical profile over thirty-six feet into the air, recycling Lake Fibonacci with freshly oxygenated water. The view is especially refulgent with the interplay of stone, water, sunlight, and fog. The profile of the fountain in the usual x, y, z coordinates approximates
for the usual Fibonacci two-term recursion sequence, fn = fn–1 + fn–2, n > 1, f0 = 0, f1 = 1. I located water cannons at Fibonacci number intervals along the ?-axis in the y = 0 vertical plane. Restricted to that plane, the profile gives an essential singularity curve which tends to infinity and zero as ? tends to zero from right and left, respectively: a smooth, infinitely differentiable, 
, but not analytic at x = 0, function [4].
This distinction between smooth and analytic, allowing functions of compact support, is worth celebration by itself.
To do architectural-size sculpture, I find friends with huge cranes. Assembling the fountain required a 75-ton crane. The 75 tons does not refer to the weight being lifted nor the weight of the crane. The 75 tons refers to the lift capacity of the crane as determined by the angle and length. The angle is that which the stick (extendable boom) makes relative to the crane platform; the length is how much stick is out. The crane had to stand on solid ground 100 feet from the fountain. This arrangement created a balance problem: A 1500-pound granite slab hanging from 140 feet of stick, at a low angle, could have tipped the crane into the squishy mud of the lake bed.We avoided this disaster by loading a 2-ton block of quartz diorite (which I happened to have in my studio) onto the back of the crane. There were dicey moments; fortunately, no one was injured.
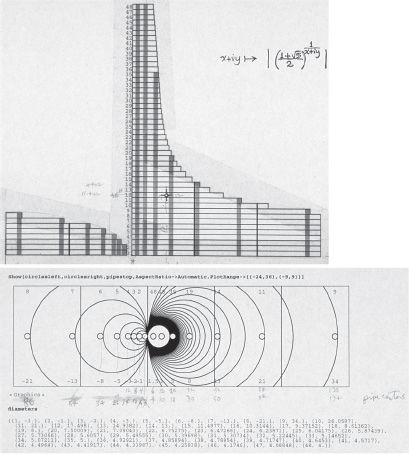
Figure 4. Reprinted by permission of Claire and Helaman Ferguson.
PIGEONHOLES AND GAUSS
I composed the fountain of layers of 1500-pound slabs, each nominally 4 inches thick.
In Figure 4 are side and plan drawings of the fountain, the x—z plane section and the projection on the x—y plane, respectively. The nominal 4 inches meant that the slabs came out of the quarry mill no thinner than 4 inches and no thicker than 4-1/2 inches, so any two slabs could differ in thickness by as much as a half inch. Stacking up half-inch differentials could have been disastrous. What to do? Use the powerful pigeonhole principle from number theory, of course.
I had eighty slabs of two colors of billion-year-old Texas granite, forty of each color from which to choose. I knew that at least two of these 1500-pound “pigeons” were within 1/64 of an inch difference. I calipered all these “pigeons” and found the usual normal distribution, from which I could select compatible subsets of “pigeons” for each layer.
Figure 5 gives a comparison and a conflict. On the bottom, the sheet records the tally marks for the distribution of the eighty slabs within the half inch. There are two, one for the forty red slabs and the other for the forty beige slabs. You can see each has the expected normal bulge in the middle. On the top we have the lovely abstraction, a Gaussian distribution, the familiar bell-shaped, unimodal curve and probability measure on the real numbers,
In the bottom image we see messy discrete reality. In the top image we see clean continuous theory with the transcendental π thrown in for good measure. I created this sculpture as I create all my sculptures, by balancing the tension between these two: ugly or beautiful, truth or ideal, or sometimes the other way round.
Note that I have not drawn the normal curve as a narrow inky line on a blank background. In fact, I have not drawn the curve at all. Instead I painted a red region and a blue region. This is more like a sculpture for me. It reminds me of the stone and air interface I create when I make a sculpture, where I spend so much time and energy to get it just right.
LIGHTNING STRIKES!
I spent three years working on this Fibonacci Fountain. Then, three years after it was installed, a lightning bolt obliterated several of the granite-enclosed water cannons. I was close enough to hear the monster thunderclap and to see the flash. Such an event might have struck me in particular as ill-fated or portentous, for, at the age of three, I had seen my natural mother killed by lightning. Fortunately, I have grown out of feeling superstitious about threes. I in fact consider three a very helpful first odd prime number.
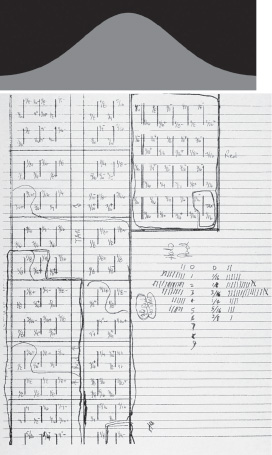
Figure 5. Reprinted by permission of Claire and Helaman Ferguson.
This lightning bolt reminded me that even if I work in billion-year- old granite as a hedge against the future, I only fob off nature for a little while. She moves on indifferent to our little interruptions.
After the strike, a scuba-diver/mathematician friend brought up three hundred pounds of granite shards, very sharp, like broken glass, which had been blown off the fountain. To prevent future strikes, I put a charge diffuser on the fountain of the sort engineers put on antennae to protect them from environmental high voltages and currents. The reconstructed fountain once again rejuvenates the lake with fresh oxygen and gathers geese under its mists.
INVISIBLE HANDSHAKE I
For this negative Gaussian curvature carving, I started with a twenty-four- ton block of two-billion-year-old black quartz diorite from South Africa.
MINIMAL vs. NEGATIVE GAUSSIAN CURVATURE
Geometer Alfred Gray inspired this negative curvature direction in my sculpture when he introduced me to Celso Costa's minimal surfaces with torus topology [7].
About each point (x, y, z) on a smooth surface S in 3, there is a little circle image on the surface. Each point of the circle has a plane through the normal to the (x, y, z) point. The plane intersects the surface S in a curve. Each curve has its own signed curvature. This mapping from the little circle to curvatures is bounded, so there will be a maximum and minimum curvature at the point (x, y, z), the two principal curvatures Kmax(x, y, z) and Kmin(x, y, z), respectively. The product of these two curvatures is the Gaussian curvature at the point (x, y, z). Gauss proved that this product curvature is an intrinsic invariant of the surface S. Isometric deformations of the surface S will have the same product curvature.
A surface S is a minimal surface if the two principal curvatures are equal in absolute value and opposite in sign at every point (x, y, z),
Weierstrass parametric representations [7] of minimal surfaces are given by the real or imaginary part of the mapping
where f and g are suitable meromorphic functions of w, and z, z0 are in a suitable region of the complex plane.
These Weierstrass parametric representations provide uncountably many immersions of minimal surfaces in three dimensions. What can I do with uncountably many virtual sculptures? I can at least sample them with stereo-pair computer graphics and pick ones I particularly like. It is possible to compute images from integrals with modern tools such as Mathematical.
What does Gaussian curvature mean to me sculpturally? The robust physical idea is not the equality of the two principal curvatures. The robust sculptural idea is that the Gaussian curvature must satisfy an inequality and be negative,
K(x, y, z) < 0.
This observation has far-reaching consequences for my sculpture: every point on a negative Gaussian curvature surface has a saddle neighborhood. Translated into stone, the idea means that locally every point is the keystone of a fabric of arches with the warp bending one way and the weft bending the opposite way. Such stone carvings should have great structural strength, and they do. Translated to anatomy, the idea lets us recognize many epithelial saddle forms on our skin surface. For instance, in the common handshake two people press together their matching negative Gaussian-curvature parts between the thumb and palm.
For me, the consequences of negative Gaussian curvature became solid in sculptures of Costa's embeddings and Weierstrass's immersions of triply punctured tori in 3. I related this to elliptic curves y2 + x3 + ax + b and a Kepler law (Jupiter shaking hands with the Sun).
I carved my early negative Gaussian curvature sculptures in Carrara marble using virtual-image projection systems. These were based on Stewart platform and cable metrology ideas. The old concept is subtraction again: carve away what is not supposed to be there. New technology allows me to virtually project the image given by parametric equations into a block of stone. Most importantly, in the midst of all this technology, I have been able to learn new negative Gaussian curvature forms and carve them directly [4]. Mathematics can be my invisible model.
CARVING QUARTZ DIORITE
The Invisible Handshake block of quartz diorite was unusually large as quarry blocks go. Upright, this block stood nine feet high, six feet wide, and five feet thick. My block came by boat into the port of New Orleans from South Africa, was barged up the Mississippi River to Minnesota, and then trucked to my studio. At twenty-four tons, this block was a single semi-trailer truckload barely below the limit for a legal load on the highway. I used a seventy-ton crane to lift my block off the truck and ease it down into my studio, where I could finally sink my diamonds into it.
Figure 6. Reprinted by permission of Claire and Helaman Ferguson.
I cored the first hole and changed forever the topology, transforming the block from simple connectivity into a torus. I built and rebuilt scaffolding to carve the torus further into a triply punctured torus.
I do not suggest that such a carving project is easy, even with new diamond cutting technology. Carving uses many tools, my diamond chain- saw principal among them.
FINAL SETTING AND FOOTPRINT
A ten-foot-diameter granite disk provides the setting for my Invisible Handshake I, tiled by hyperbolic pentagons. The footprint of the sculpture is the center right-angled pentagon of 2-1/2-foot radius.
Figure 7. Fibonacci Fountain. Reprinted by permission of Claire and Helaman Ferguson.
I created a computer-graphics color image of the hyperbolic checkerboard of right-angled pentagons in the Poincare hyperbolic disk, with the figure five moving, tense, but heeded through the hyperbolic plane. This was my response to the imagist poem “The Figure Five” by William Carlos Williams and the subsequent painting by his friend Charles Demuth.
On the right side I've transferred these right-angled hyperbolic pentagons into a fabric sculpture quilt, a negative Gaussian-curved checkerboard of identical panel pentagons. This quilt adapts itself well to the human form and, like the human form, it can be flattened locally but not globally. The finished stone carving Invisible Handshake weighs 7-1/2 tons and has a precisely carved pentagonal footprint. This corresponds to the central pentagon of a Poincare disk ten feet in diameter hyper- bolically tiled in two colors of granite. On the left is a small bronze analog of this setting with a hyperbolic pentagon footprint.
The sculpture fits into the space of this central tiling of a conformal Poincare disk. The closed necklace of corner-connected pentagons is in number 5 times every other Fibonacci number (those ubiquitous rabbits) [15].
THE NINE-TON BELL REVEALS ITSELF
I had carved the twenty-four-ton block down to a little over nine tons. To prepare to carve the right-angled pentagon footprint, as shown with attached water-jet precision-cut template (Figure 8 on right), I laid the block on one side. To do this simple move, I hired a sixty-ton crane, a crane operator, and a rigger man. We had everything rigged up for the tricky rotation. The nine-ton sculpture hung horizontally about four feet off the concrete floor. While I was changing the timber cribbing, I heard a crackle. The sculpture had slipped about an inch, which created enough friction to melt the thick six-inch-wide nylon rigging strap. The nine tons struck the floor, with one corner crushing a six-inch hole in the concrete. It rang like a bell! No evidence of this mishap showed on the piece, which was not what I would have expected given a big block. I would have assumed that such a force on a point would split the block.
Figure 8. Reprinted by permission of Claire and Helaman Ferguson.
I learned later that the velocity of sound in this quartz diorite is greater than the velocity of sound in steel, even though the density of steel is much greater than any stone. The negative Gaussian curvature form has saddle (double-arch) forms everywhere. An upright arch is quite strong in relation to gravity. Because a negative Gaussian curvature form presents a web of arches, every point is a keystone with a double arch regardless of the orientation relative to gravity. This gives the sculpture great strength even though the curved form is practically hollow compared to its original solid form. Evidently the energy from the force of impact is radiated almost instantly and uniformly throughout the sculpture.
I should not have been too surprised about this, because I had been carving negative Gaussian curvature forms in stone and had noted their bell-like aspects. I had also noted the peculiar strength of the negative
Gaussian curvature form in a large snow (not ice) carving I did that softened in the sun but did not collapse.
Negative Gaussian curvature surfaces, especially minimal surfaces, must have infinite extent in 3. To create a sculpture I have to terminate the surface. Rather than follow the quarry faces of the raw block, I now choose to compute an appropriate wave front boundary by solving the Gauss-Christoffel equations for geodesics on a surface in R3 [7]. The primary pressure wave will radiate along geodesics.
Future
My current sculpture studio is in an industrial park in Baltimore, Maryland. My studio volume is 45,500 cubic feet. My “tool box” is a shipping container, which when filled with hand tools weighs 14,000 pounds. As I sit here, I feel in my mind my thirteen-ton block of beautiful billion- year-old Texas red granite, and my fingers sweat. This raw granite block compels me to think of the right timeless theorems. Its time is now.
References
[1] DAVID H. BAILEY, Integral relation detection, Communications in Science and Engineering, Top 10 Algorithms of the Century: 24–8, January/February 2000.
[2] JAMES A. CANNON, Mathematics in marble and bronze: The sculpture of Helaman Rolfe Pratt Ferguson, The Mathematical Intelligencer 13 (1991), no. 2, 30–9.
[3] SIMON PLOUFFE, DAVID H. BAILEY, and PETER B. BORWEIN, On the rapid computation of various polylogarithmic constants, Mathematics of Computation 66 (1997), no. 218, 903–13.
[4] CLAIRE FERGUSON, Helaman Ferguson: Mathematics in Stone and Bronze, Meridian Creative Group, Erie, Pennsylvania, 1994.
[5] HELAMAN R. P. FERGUSON, Two theorems, two sculptures, two posters, American Mathematical Monthly 97 (1990), no. 7, 589–610.
[6] HELAMAN R. P. FERGUSON, Analysis of PSLQ, an integer relation finding algorithm, with David H. Bailey and Steve Arno, Mathematics of Computation 68 (1999), no. 225, 351–69.
[7] ALFRED GRAY, Modern Differential Geometry of Curves and Surfaces with Mathematica, xxiv+1053 pages. CRC Press, Boca Raton, second edition; Chapter 22.2 is Gauss's Theorema Egregium; Chapter 32, pages 735–60 is on minimal surfaces via the Weierstrass representation (not in the first edition), 1998.
[8] HOWARD TRACY HALL, Ultrahigh pressure research: Tetrahedral anvil press, Science 128 (1958), 445–9.
[9] SCULPTOR HELAMAN FERGUSON, Eightfold Way, volume Carrara White Marble and Albemarle Virginia Serpentine, Mathematical Sciences Research Institute, 17 Centennial Way, Berkeley, California, 1993.
[10] SCULPTOR HELAMAN FERGUSON, Four Canoes: Two Linking Klein Bottles, volume 12 tons with plaza, billion-year-old Texas red granite, half-billion-year-old Academy Black California quartz diorite. University of St. Thomas, Sabo Square, University of St. Thomas, corner of Cretin and Summit Avenues, St. Paul, Minnesota, 1995.
[11] SCULPTOR HELAMAN FERGUSON, Clay Mathematics Institute Award, Clay Mathematics Institute, Cambridge, Massachusetts, 1998–present.
[12] SCULPTOR HELAMAN FERGUSON, Fibonacci Fountain:Essential Singularity II, volume 42 tons of red and beige Texas billion-year-old granite, concrete, and steel. Dean Morehouse, Lake Fibonacci, Maryland Science and Technology Center, Bowie, Maryland, 2000.
[13] SCULPTOR HELAMAN FERGUSON, Invisible Handshake I, volume 9 ft × 5 ft × 6 ft, negative Gaussian curvature carving; base is 10-ft diameter hyperbolic disk tiled by right-angled pentagons forming a checkerboard in two colors of granite. Merck Pharmaceutical, Upper Gwynedd, Pennsylvania, 2002.
[14] SCULPTOR HELAMAN FERGUSON, David and Bessie Borwein Award, CMS/SMC Career Award. Canadian Mathematical Society, 2004–present.
[15] SCULPTOR HELAMAN FERGUSON, Five-Fold Negative Gaussian Curvature, volume two-part bronze, triply punctured torus with right-angled pentagon footprint, cuneiform-inscribed Poincare disk, 2005.
[16] SCULPTOR HELAMAN FERGUSON, SYZYGY: Venus and Mars redux, volume billion-year-old Texas red and beige granite, articulated Poincare discs with Mayan Mars and Venus pyramids. Hamilton College, in front of the Science Center, Hamilton College Campus, Clinton, New York, 2006.
[17] SCULPTOR HELAMAN FERGUSON, Invisible Handshake II, volume 3-ton quartz diorite, half- billion-years-old, negative Gaussian curvature, Macalester College, Olin-Rice Science Center, Macalester College, St. Paul, Minnesota, 2008.
[18] SCULPTOR HELAMAN FERGUSON, AMS Public Service Award, American Mathematical Society, 2009–present.
[19] SCULPTOR HELAMAN FERGUSON, Gauss Society Donor Award, Mathematical Sciences Research Institute Gauss Society, 2009–present.
[20] SCULPTOR HELAMAN FERGUSON, Stephen Anson Coons Award, career award. ACM/SIG- GRAPH, biennial, 1999–present.
[21] IVARS PETERSON, “Fibonacci Fountain,” Science News, 2002.
[22] KATHERINE UNGAR, Helaman Ferguson: Carving his own unique niche, in symbols and stone, Science 314 (2006), no. 373, 412–3.