Seeing Numbers

 

IVAN M. HAVEL

The ability to represent time and space and number is a
precondition for having any experience whatsoever.

—Randy Gallistel

In his influential book The Principles of Psychology (1890) the well-known psychologist and philosopher William James listed seven “elementary mental categories” that he postulated as having a natural origin [Jam07, p. 629]. In an alleged order of genesis he listed, in the third place, after the ideas of time and space, the idea of number.

Mentioning the idea of number along with the ideas of time and space as something natural is interesting both philosophically and from the viewpoint of cognitive science. In this respect it is worth noting that one of the symptomatic features of mainstream cognitive science is the tendency not to talk so much about ideas as about their representations, either in the mind or, even better, in the brain. Just notice the maxim by Randy Gallistel in the above motto (quoted in [Cal09]). The hypothesis that the human sense of number and the capacity for arithmetic finds its ultimate roots in a basic cerebral system has been frequently proposed and elaborated, for instance by the neuroscientist Stanislas Dehaene [Deh97, Deh01, Deh02].

In this essay I am going to take up a somewhat different perspective.¹ Instead of following up with various extraneous concerns offered by brain research and behavioral and/or developmental psychology I will base my considerations on the way things, in our case numbers,² are actually experienced (a digression towards animal “arithmetic” in a subsequent section is an exception). Hence the nature of my interest is more phe- nomenological (in the philosophical sense of the word) than scientific and, I dare say, my claims are speculative, rather than conforming to empirical or deductive knowledge. Correspondingly, I use the term “experience” in its philosophical sense, when referring to any mental state associated with one's conscious “living through” a certain event or situation—“conscious” in the sense that there is something “it is like” to be in that state of the mind.

First of all we should make clear what kind of “thing” numbers are, i.e., what is the nature of entities that humans may experience as numbers? The way mathematicians formulate, introduce, or conceptually represent their idea of a number is quite a different question. This, however, does not mean that the relation between the mathematicians' concept and human experience should be ignored as irrelevant.

Our first observation is that the very word “number” (in English as well as its equivalents in some other languages) is rather multivalent. This fact may lead to difficulties, especially in the context of our study— but, at the same time, it may hint at certain interesting hypotheses about the origin of this very multivalence. Thus I shall distinguish here at least three different senses of the word: (1) “numbers” as numerical quantities, i.e. counts of something, (2) “numbers” as abstract entities emerging in the human mind and allowing mathematical formalization in the framework of one or another formal theory,³ (3) “numbers” as natural or conventional symbols or numeral signs that represent numbers in either one of the previous two senses. In view of the importance of this conceptual distinction in our study, I shall henceforth distinguish the above three senses by using, respectively, the terms (1) count, (2) number, and (3) numeral. However, when there is no danger of confusion, I shall often use the term number in the general, more encompassing sense.

Human Sense of Numerical Quantities

Are we, people, endowed with anything like a sense of counts? Here the term “sense” (another multivocal word) vaguely refers to human ability or disposition to recognize some (not too large) counts of items that are perceived, remembered, or imagined. The allusion to perceptual “senses” (vision, hearing, touch, etc.) may be intuitively apt but it is worth elaborating a little (cf. [Hav09a, Chapter 5]).

Let us start with the intended meaning of the general notion of having (or being endowed with) the sense of X where X is a certain predetermined quality (in our case, somewhat oddly, the term “quality” refers to numerical “quantity”). First, such “sense” is something to be attributed to a person who is, so to speak, the possessor or owner of the said sense, and second, “having the sense of” refers to one's disposition, rather than to factual employing such disposition in a concrete situation (analogically to, say, the sense of humor, sense of responsibility, etc.). This subtle distinction is not always properly taken care of in the scientific literature but it is usually implied by the context. It may turn out to be particularly relevant to cognitive science which attributes various “senses of…” or “feelings for…” to conscious subjects. I shall call such subjective dispositions, or “senses of something,” simply inner senses (take it just as a technical term).

Most such inner senses are implicit, pre-reflective features of our everyday experience even if sometimes we may subject them to conscious reflection, especially when they are actually being employed. This holds, mutatis mutandis, for the usual perceptual senses as well as for the sense of counts. All of them are subjectively experienced as well as objectively inferable dispositions. Unlike perceptual senses, the sense of counts does not have its own dedicated physiological organ; rather it indirectly utilizes various perceptual organs (as for its dedicated brain area there exist various conjectures).

We may tentatively put forth the idea of a minimal, pre-reflective inner sense of counts as something innate, already built into the very structure of experience. For this, however, we would have to distinguish various subcategories of counts: depending on whether they correspond to small, moderately large, or very large numbers (prematurely said).

Indeed, we directly perceive, without counting, very small counts.⁴ For instance, we normally “see at a glance” the triplicity in triangles or tripods, quaternity in squares, quintuplicity in five-point stars—all that without any actual process of counting angles (or legs or vertices or tips)—but when the group becomes larger we gradually become wrong in a direct grasp of the count. This may happen around seven, eight, or more items in the group (depending on the individual and context). For larger groups we cannot but resort to a slower but more reliable actual counting procedure. Let us refer to this transition phase as to the first horizon of number apprehension. Then the second horizon of number apprehension might vaguely delimit what can be conceivably counted in practice (possibly in thought only); finally, numbers that are beyond the second horizon and stretch towards the potential infinity can only be grasped through indirect theoretical tools.

The sense of counts should be distinguished from another, perhaps originally independent inner sense of numerosity comprising the ability to notice that a certain group of entities either swells or shrinks, or that it is either larger or smaller than another group of entities. The sense of numerosity need not entail, in general, the ability of counting or the idea of a count.

Let us quote W. James' account of (the sense of) counts, namely the ideas of number, of the increasing number-series, and of the emergence of arithmetic [Jam07, pp. 653—4]:

Number seems to signify primarily the strokes of our attention in discriminating things. These strokes remain in the memory in groups, large or small, and the groups can be compared. The discrimination is, as we know, psychologically facilitated by the mobility of the thing as a total. But within each thing we discriminate parts; so that the number of things which any one given phenomenon may be depends in the last instance on our way of taking it. […] A sand-heap is one thing, or twenty thousand things, as we may choose to count it. We amuse ourselves by the counting of mere strokes, to form rhythms, and these we compare and name. Little by little in our minds the number-series is formed. This, like all lists of terms in which there is a direction of serial increase, carries with it the sense of those mediate relations between its terms which we expressed by the axiom “the more than the more is more than the less.” That axiom seems, in fact, only a way of stating that the terms do form an increasing series. But, in addition to this, we are aware of certain other relations among our strokes of counting. We may interrupt them where we like, and go on again. […] We thus distinguish between our acts of counting and those of interrupting or grouping, as between an unchanged matter and an operation of mere shuffling performed on it. […] The principle of constancy in our meanings, when applied to strokes of counting, also gives rise to the axiom that the same number, operated on (interrupted, grouped) in the same way will always give the same result or be the same.

Some authors use the term number sense for “our ability to quickly understand, approximate, and manipulate numerical quantities” [Deh01]. In this study I dare to claim, probably despite James, that our ability to perform actual counting (above the rudimentary sense of counts) may not be a necessary prerequisite for the number sense. In my view, two inner senses—the direct sense of (small) counts and the sense of numerosity—may be more essential.

Can Animals Count?

There is a growing number of studies with animals exhibiting certain limited abilities to count and, as it is often claimed, to perform elementary arithmetic operations [Cal09]. We may be enticed to immediate hypotheses about the evolutionary origin of such abilities. This, under the prevailing Darwinian paradigm, would make us look for one or another survival advantage of such abilities, analogous to the advantages of having, say, the sense of colors, of shapes, of spatial directions, etc.

Perhaps we may conjecture that what appeared relatively early in the animal world might have been abilities that are not based on the process of counting. Such abilities may be primarily two: (1) the ability to identify small counts at a glance—a count of eggs, offspring, wolves in a pack, etc.—and (2) the ability to distinguish, without counting, between a smaller amount and a larger amount—of grain, leaves of grass, ants in a colony, etc.—(as James puts it, “the more than the more is more than the less.”) Only much later, perhaps among humans, actual counting procedures came to be used, and after that there emerged the abstract concept of a number together with the idea of the “number line” endowed with various arithmetical operations.

Various experiments show that there are certain reasons to attribute the sense of (small) counts to animals. There are reports on primates, elephants, salamanders, chimpanzees, birds, even fish and bees, which can reliably recognize small counts of presented objects [Cal09]. The favorites are four-day-old chicks (thus no training could be assumed) that reportedly are able to correctly determine that 1 + 2 is greater than 4 — 2, that 0 + 3 exceeds 5 — 3, and that 4 — 1 is more than 1 + 1. However, one has to be careful with interpreting such experiments. Researchers frequently use certain appealing phrases like “number recognition” or even “arithmetic skills” when talking about animals. My own small survey of the literature has revealed, first, that such experiments with animals involved counts of some specific objects, usually objects with survival importance to the animal. Second, in most cases the tested abilities could be explained simply by the ability to discriminate between larger and smaller amounts, without any need to do actual counting. (The rash claims about “arithmetic” skills of animals could be enticed by the habitual tendency of us, numerate humans, to do counting, adding, subtracting, etc., even when we deal with relatively small counts.)

There are two suitable ideas that may support various hypotheses about evolutionary origins of the number sense. One idea was already mentioned: looking for obvious survival advantages. The second idea is more logical. For instance, the sense of counts already presumes other inner senses, namely the sense of sameness and difference, or more specifically, the sense of individuality of elements of a group and the sense of that very type of similarity which characterizes the group. (Surprisingly enough, James placed “ideas of difference and resemblance, and of their degrees” into a later, fourth position in his list of natural mental categories.)

Representing Numbers

How did we, the human species, develop the abstract concept of a number, as something implicitly related to counts but without reference to particular entities counted? Talking and thinking in a human way about abstract numbers is only possible with their appropriate symbolic rep- resentations.⁵ Here comes the third meaning of the word “number,” viz. that of a numeral. Let us use this word in the most general sense, including not only word numerals (like “one,” “two,” “three”,…) and their combinations (“thirty-six”) but also other kinds of symbol, or better, sets of symbols, that unambiguously represent (abstract) numbers. You can think of the usual graphical signs (1, 2, 3, 4,…, or 01, 10, 11, 100,…, or I, II, III, IV,…). Let us allow, for the purposes of the present study, even more general representations, for instance geometrical shapes, whether drawn, written, or merely imagined.

To avoid misunderstanding: I do not assume that the concept of numeral has to be derived from, or dependent on, a prior concept of (abstract) number. We could equally well associate numerals directly with counts of some entities, real or imagined. The simplest idea is the analog representation of counts (or numbers). Think, for instance, of scribbling down or imagining groups of some concrete objects like dots, strokes, tokens, marks, knots on a rope, etc.⁶ Each such group can be also viewed as a symbolical numeral directly representing the count of items in the same group. In mathematics we speak about the unary numeral system for representing numbers.

Figure 1. Numeral signs in various cultures (redrawn from [Ifr94]).

As a matter of fact, many cultures use analog notation (signs) for three smallest numbers, sometimes even for four or five; see Fig. 1. Obviously, for slightly larger numbers (near the first horizon of number apprehension) a danger of misinterpretation may increase. Probably because of this and for the sake of compression specific signs have been used instead of analog signs. Moreover, and more importantly, arbitrarily large numbers can be represented by sequential juxtaposition of figures.

It is worth noting that some languages use different words for counts of different categories of object. This fact may suggest that the concept of count may be more natural than the concept of number.

It is interesting to note, in passing, that some languages use object-specific numeral systems which depend on the kind of objects counted [BB08]. For instance, on one of the island groups in Polynesia, tools, sugar cane, pandanus, breadfruit, and octopus are counted with different sequences of numerals. There is a current dispute about whether such object-specific counting systems were predecessors of the abstract conception of numbers and number line (Beller and Bender argue in the opposite).

Numbers Dancing in our Heads

We can follow up the above considerations in various directions. We have already observed that there are three different conceptualizations of the prearithmetic idea of number: (1) number as a count of some identifiable (maybe visible or tangible) items, (2) (invisible, intangible) abstract number, and (3) number as a numeral of certain type (visible, speakable, etc.). In theory we can easily point to inherent, indeed even necessary, interrelationships between these three conceptualizations. For instance, we may be interested in comparing three respective roads to infinity: (1') the intuition of gradual but unbounded swelling the group of items toward larger and larger counts (passing over the first two to the third of the above mentioned horizons of number apprehension), (29) developing a formal (axiomatic) theory of natural numbers, and (3') assuming such numerical representations that allow for depiction of arbitrarily large counts (or of arbitrarily large abstract numbers).

I am not going to discuss the theoretical issue of infinity here. Instead I am going to pose a different question, which may be more important if human cognition is at issue. Let us look “inside our minds,” so to speak, and ask whether and how far we (humans) could mentally grasp the idea of a number.⁷ If we are able to “see at a glance” (i.e., without counting) small counts of things, why not venture into imagining an analogously direct access to much larger counts, or perhaps even to abstract numbers?

True, in our culture we are too captive in the framework of words (numerals), symbols (number signs), arithmetic operations, and indeed, of the whole number line. Speaking for myself, whenever I hear, say, the sound “thirty-six” I immediately happen to hear “six times six” (as a leftover of memorizing the multiplication table in primary school), or alternatively, I could imagine the formula “36 = 2² 3²” (provided I were obsessed with prime number representations). Surprisingly enough, I never imagine a rectangle of six rows and six columns of dots (or something), or a prism made of small cubes, four horizontal, three vertical, and three backwards. Why not? Wouldn't it be easier to form mental images of various geometrical shapes, to remember them, and perhaps to manipulate them in various exciting ways?

Consider for example Fig. 2. In its upper part there are nine groups of dots; each group corresponds to a different count of dots (a singleton, pair, triplet, quartet, etc.). Let us fix the relative position of dots in each group by shaded lines. In the lower part of Fig. 2 only the lines are depicted. Why not treat these line figures as numeral signs, easy to be imagined and remembered? Notice that most of these figures areformed by adjoining previous figures in the sequence; this immediately leads to the tentative idea of using such an adjoining process for picto- rially representing much larger numbers. Incidentally, each such numeral can be viewed as both analog and symbolic representation of a certain number.⁸ (In one of the following sections this representation will be used to develop a more expressive pictorial representation of numbers.)

Figure 2. Turning dots into figures.

There is a plausible hypothesis that autistic savants with extraordinary numerical powers can mentally grasp numbers in some synesthetic way (pictorial, auditory, tactile), or maybe even in a form of some dynamic objects, rather than in the ordinary numeral representation.⁹ In this respect it is worth mentioning the case of Daniel Tammet (known for his record of reciting 22,514 digits of P from memory). Let me quote some of Tammet's own reflections (from a recently published conversation with him in Scientific American [Leh09]):

I have always thought of abstract information—numbersfor example—in visual, dynamic form. Numbers assume complex, multi-dimensional shapes in my head that I manipulate to form the solution to sums, or compare when determining whether they are primes or not. […] In my mind, numbers and words are far more than squiggles of ink on a page. They have form, color, texture and so on. They come alive to me, which is why as a young child I thought of them as my '“friends.” […] I do not crunch numbers (like a computer). Rather, I dance with them. […] What I do find surprising is that other people do not think in the same way. I find it hard to imagine a world where numbers and words are not how I experience them! […My] number shapes are semantically meaningful, which is to say that I am able to visualize their relationship to other numbers. A simple example would be the number 37, which is lumpy like oatmeal, and 111 which is similarly lumpy but also round like the number [numeral figure] three (being 37 X 3). Where you might see an endless string of random digits when looking at the decimals of P, my mind is able to “chunk”groups of these numbers [figures] spontaneously into meaningful visual images that constitute their own hierarchy of associations.

This is a rare case of a savant able to report on his exceptional inner experience. No wonder such a report generates more questions than answers. As I already mentioned, contemporary discussions mostly seek solutions from brain research, which is expectable in view of the tremendous recent progress in various brain imaging techniques. My opinion is, however, that we could hardly expect from the brain scientist direct and valuable answers to phenomenally formulated questions about subjective experience. When Tammet says, for instance, that numbers “assume complex, multi-dimensional shapes,” or that he “dances with them,” it is of little help to the neuroscientist in his quest for adequate phenomena in the brain. By no means do I want to say that Tammet's reports are meaningless—quite conversely, I believe that his semi-metaphorical statements say more, in a sense, about the human mind than the empirical scientist could formulate in the language of neuronal dynamics.

The Riddle of Prime Twins

Here “prime twins” is a little pun: I do not mean twin primes (i.e. prime numbers of the form p, p + 2), but John and Michel, the famous autistic, severely retarded twins, studied in 1966 by the neurologist Oliver Sacks [Sac85]. I am not going to discuss here their significance for scientific (neurological or psychological) research but merely use them as a valuable source of, or motivation for, wild hypotheses about the way the human mind can deal with numbers in the extreme. Let us quote Sacks' own report on one of his encounters with the twins [Sac85, p. 191]:

[They] were seated in a corner together, with a mysterious, secret smile on their faces, a smile I had never seen bJore, enjoying the strange pleasure and peace they now seemed to have. I crept up quietly, so as not to disturb them. They seemed to be locked in a singular, purely numerical, converse. John would say a number—a six-figure number. Michael would catch the number, nod, smile and seem to savour it. Then he, in turn, would say another six- figure number, and now it was John who received, and appreciated it richly. They looked, at first, like two connoisseurs wine-tasting, sharing rare tastes, rare appreciations. I sat still, unseen by them, mesmerized, bewildered.

Sacks wisely wrote down their numbers and later, back at home, he consulted a book of numerical tables and what he found was that all the six-figure numbers were primes! The next day he dared to surprise the twins and ventured his own eight-figure prime. The twins paused a little time and then both at the same time smiled. The exchange of primes between Sacks and the twins continued during the following days, with gradual increase of the length of the numeral up to one of twenty figures brought out by the twins, for which, however, Sacks had no way to check its primality. For generating and recognizing larger primes the twins needed more time, typically several minutes.

Let us point out four conspicuous aspects of the twins' performance: (i) their striking emotional fondness for the primes, even if (ii) “they [could] not do simple addition or subtraction with any accuracy, and [could] not even comprehend what multiplication or division means” [Sac85, p. 187], (iii) there were delays in their reactions—the larger the longer numerical lengths of the primes processed, and (iv) there were certain indications that visualization was at play, as Sacks writes about another of the twins' abilities (calendar calculation) [Sac85, p. 187]:

[Their] eyes move and fix in a peculiar way as they do this as if they were unrolling, or scrutinizing, an inner landscape, a mental calendar. They have the look of 'seeing', or intense visualization […]

One of the above listed aspects (the third one, about delays) may suggest that production or recognition of a prime was not an instantaneous act but involved a certain internal “procedure” that consumed a certain time—a nontrivial time compared to the usually instantaneous responses of number prodigies. Well, what may such a procedure be?

It is not my intention to put serious effort into trying to explain the particular extraordinary powers of Sacks' twins¹⁰ (or other number prodigies). I rather take up the twin case as an incentive to deal with numbers in alternative ways, not grounded in ordinary arithmetic.

Primality sans Arithmetic

A simple characterization of primes which is not based on arithmetical operations may be as follows: A number is a prime if and only if it corresponds to the count of items that cannot be arranged into a regular rectangle (except for a row or line). Imagine, for instance, a platoon of soldiers that cannot be drawn up into a rectangular formation (file by three, file by four, etc., except for a single row or line). Then we can easily design an effective finitary procedure P which, given a group X of individual elements (let us call them tokens), would systematically arrange it into various rectangular formations, always checking whether some of the tokens are left over or not. If the only possible arrangement without a leftover is a single row (or line) then the count of all tokens in X is a prime number.

The following four observations about such primality test P seem to be particularly relevant to our approach: (1) the procedure P may be carried out, in principle, with the help of visual imagery only, (2) feasibility of P in imagination could reach a certain (biological or psychological) limit if X happens to be too large, (3) the larger X the more steps may P require (hence more time would be needed for realizing P), and, last but not least, (4) in order to execute P there is no need to know the precise (numerical) count of tokens in X. What is only needed is a presentation of group X as a whole and allowing for simple mobility of its tokens. (Incidentally, one can imagine a mechanical apparatus that would realize the procedure).

Now, the oddity of prime number prodigies may be primarily related to point (2). With the current relatively moderate (albeit rapidly growing) scientific knowledge of the structure and dynamics of the brain, and without any knowledge at all about inner experiences of the prodigies, we can only conjecture that, for the prodigies, the feasibility horizon of procedure P must be substantially farther than for normal people.

Of course, there may exist (and probably do exist) some unimaginable, entirely different solutions for dealing with primes. We are still far from understanding even the particular case of Sacks' prime twins. How, in addition to some marvelous mental imagery, were they able to communicate about numbers also in the ordinary form of (Arabic) numerals or (English) words? And why did they sense precisely primes as something joyful?

Numbers Turned into Curves

Following up with the first question (about communication), I shall develop here an illustrative example of a relatively simple direct translation between two types of number representation: on the one hand, numerals in the usual form of sequences of decimal digits (or expressions formed from number names), and on the other hand, made-up pictorial “numerals” representing even huge numbers, preferably in a way that would allow “seeing them at a glance.”

Let us discuss the latter issue, that of pictorial representation. To be more specific, consider the numeral system introduced in one of the preceding sections (cf. Fig. 2). There I mentioned the possibility of extending such system to arbitrarily large numbers. However, the presumed miraculous imagery of even the most prodigious savants cannot be unbounded. Under the theory of embodied mind, whatever the (yet unknown) nature of pictorial number representation may be, there have to be certain limits to it. Such limits could somehow resemble the first horizon of human direct number apprehension (as mentioned in the second section of this text), except that they may be located considerably far away (“far away” on our number line).

My speculative idea for a more powerful savant number representation (assume that it can be still called “representation”) is based on the notion that it may have a hierarchical nature.¹¹ I shall illustrate it with a concrete example (admittedly fabricated and most likely without any relation to reality). In the first step choose a certain, perhaps small set N₀ of elementary numerals, for instance the nine figures in Fig. 2. This determines the first level of number representation. In the next step arrange elements of N₀ into a predetermined fixed formation, let us say into a 3 X 3 regular grid G(9) with one additional point (for zero), as shown in Fig. 3. Obviously, in the Euclidean plane this grid can be uniquely determined by three reference points (a, b, c), also depicted in Fig. 3.

Imagine now a certain number n presented in the form of a decimal numeral (sequence of digits), say, n = 5 950 425 853. Draw a smooth curve through the grid, starting in point a and successively passing through all and only those vertices that represent digits 3, 5, 8, 5, 2, 4, 0, 5, 9, 5 in that order (for technical reasons in the reverse order comparing to n). There may be infinitely many such curves but each would represent precisely number n (one of them is the upper left curve in Fig. 4, the other curves in the figure represent other numbers; I included them for the readers who like pictures).

For the inverse procedure, consider a given planary curve (for instance one of those in Fig. 4) together with three reference points, a, b, and c. These points are sufficient to draw a unique regular grid (as in Fig. 3) that lies over the curve. Now proceed along the curve, starting in the upper point a, and list all the digits associated with vertices you pass through (you should list them from the right to the left). Eventually the generated numeral expresses the unique number represented by the curve.

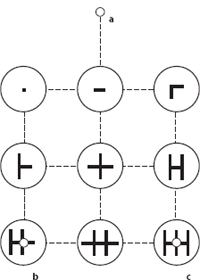
Figure 3. First level of number representation.

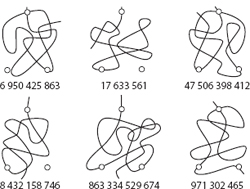
Figure 4. Second level of number representation.

I admit that the procedure is somewhat artificial and strange. Moreover, it has a serious drawback (for our approach): even if it is thinkable that the curve itself can be recognized at a glance (analogously to, e.g., human face recognition), the snag is the requirement of knowing its exact position with respect to three fixed reference points. Yet the proposed procedure has certain noticeable properties: first, one can in principle get along with visual imagery, second, there is no need of counting anything, and third, no standard arithmetical operations are used.Yet the procedure allows for handling considerably large numbers (as seen in Fig. 4) with only a modest increase of complexity.

Seeing Primes All at Once

As a matter of fact, quite a different alternative track of thought may be pursued, too. It is conceivable that number prodigies do not care so much about concrete numbers and their individual properties like pri- mality. Let me quote in this respect a passage about a synesthetic subject from [RH03, pp. 56—7]:

If asked to visualize numbers the subject finds that they are arranged in a continuous line extending from one point in the visual field to another remote point—say from the top left corner to bottom right. The line does not have to be straight—it is sometimes curved or convoluted or even doubles back on itself. In one of our subjects the number line is centered around “world centered” coordinates—he can wander around the 3D landscape of numbers and “inspect” the numbers from novel non-canonical vantage points. Usually the earlier numbers are more crowded together on the line and often they are also coloured.

Obviously a modified version of such a process may be hypothesized for the case of prime number savants like Sacks' twins. They may be miraculously gifted with a sort of direct access to a certain whole set of primes, small or large (certainly not to the set of all primes in the mathematical sense). They can perhaps visualize the entire set as a single, very complex geometrical object in which primes play a salient role, while nonprimes fill the space between or around them. A very simple illustrative example of such an idea is depicted in Fig. 5 where the ordinary number line is curved around a straight “prime-number line”.

Figure 5. Prime number line and non-prime number line.

Now is a good time to comment on the question concerning Sacks' prime twins who, even though severely retarded, paid special attention precisely to primes. Why was it just primes, out of all numbers, that made them so happy? A weird but plausible idea may be that the geometrically prominent positions of primes on or inside the complex geometrical object mentioned above would charge them with some emotionally strong, perhaps esthetic quality.

Another, easier guess may proceed from our earlier characteristic of primes: a prime number corresponds to such a count of elements of a group that wriggles out of all (nontrivial) rectangular formations. With a grain of aphorism: an entity that resists something as banal as a rectangular formation deserves a joyful welcome.

Conclusion

I outlined several purposefully simple but highly speculative ideas about mental number processing, motivated by some extraordinary cases of numerical savants. I admit that the ideas are far from being mutually compatible. The reader may have noticed, for instance, that there is no clear way to combine the curved-line pictorial representation of numbers with the procedure of primality testing. The remarkable powers of Sacks' twins and of other number prodigies remain, and probably will remain for a long time, a mystery.

However, my motivation for seeking various number representations and procedures did not consist in trying to suggest some explanatory tools and even less did it consist in proposing something of practical use. The only purpose was heuristic: to open possibilities of quite unusual lines of reasoning about cognition and arithmetic.

Dedication

This essay is dedicated to Petr Hajek, my teacher, colleague, and friend.

Notes

1. In this paper I expand on some of the ideas briefly presented in my earlier essays, e.g., [Hav08, Hav09b]. The work on this paper was funded by the Research Program CTS MSM 021620845.

2. Throughout this paper the term “number” always means “natural number.”

3. What is characteristic of abstract numbers is that they do not emerge (or they are not constructed) individually but always together with some (or all) other numbers.

4. Let us live with this little ambiguity in terms—by the verbal form (to count) I refer to an active temporal process aimed at determining the count.

5. In this point I differ from the view of some scientists like Dehaene (quoted above) and Jean-Pierre Changeux. They associate the number sense with activation of specialized neuronal circuits in the brain (this applies also to non-human animals) so that human language and consciousness are not assumed to be a prerequisite for dealing with numerical quantities.

6. Perhaps even temporal sequences of events like sounds of a tolling bell.

7. For philosophical reasons I am not comfortable with the term “introspection” but the reader may happily make do with it.

8. The adjoining procedure may lead even to 2D or 3D figures.

9. The term synesthesia refers to perceptual experience in multiple modalities in response to stimulation in one modality. For some people, for example, letters or numbers (numerals) evoke vivid color sensations [RH03].

10. In response to Sacks' report, several researchers published various theoretical speculations. However, most of them (if not all) are based on ordinary arithmetical properties of primes (cf., e.g., [Yam09]).

11. In fact, the positional numeral system is hierarchical too, since each position represents different power of 10. In our case the word “hierarchical” should point to different representational strategy associated with each level.

Bibliography

[BB08]    S. Beller and A. Bender. The limits of counting: Numerical cognition between evolution and culture. Science, 319:213—5, 2008.

[Cal09]    E. Callaway. Animals that count: How numeracy evolved. New Scientist, 2009.

[Deh97]   S. Dehaene. The Number Sense. How the Mind Creates Mathematics. Oxford University Press, NewYork, 1997.

[Deh01]    S. Dehaene. Precis of the number sense. Mind and Language, 16(1):16—36, 2001.

[Deh02]    S. Dehaene. Single-neuron arithmetic. Science, 297:1652—3, 2002.

[Hav08]    I. M. Havel. Zjitfrena mysl a kouzelny svet. Vesmir, 87:810, 2008. In Czech.

[Hav09a]  I. M. Havel. Uniqueness of episodic experience. In Kognice 2009, pages 5—24, Hradec Kralove, 2009. Gaudeamus, 2009.

[Hav09b]    I. M. Havel. Videt pocty a cisla. Vesmir, 88:810, 2009. In Czech.

[Ifr94]      G. Ifrah. Histoire Universelle des ChJJres, volume I et II. Robert Lafont, Paris, 1994.

[Jam07]    W. James. The Principles of Psychology, volume II. Cosimo Inc., NewYork, 2007. Originally published in 1890 in Boston.

[Leh09]    J. Lehrer. Inside the savant mind: Tips for thinking from an extraordinary thinker. Scientific American, 2009. www.scientificamerican.com/article.cfm?id=savants—cognition—thinking.

[RH03]    V. S. Ramachandran and E. M. Hubbard. The phenomenology of synaesthesia. J. of Consciousness Studies, 10(8):49—57, 2003.

[Sac85]    O. Sacks. The twins. In The Man Who Mistook His Wife for a Hat, pages 185—203. Pan Books, London, 1985.

[Yam09]   M. Yamaguchi. On the savant syndrome and prime numbers. Dynamical Psychology, 2009. Electronic journal, www.goertzel.org/dynapsyc/yamaguchi.htm.