Intersecting a Ray with a Cube
The intersection algorithm must decide whether a given ray intersects any of the cube’s six faces or whether the ray misses the cube altogether. Treat those two cases as tests, starting with the first one: a ray intersecting a cube.
Test #1: A Ray Intersects a Cube
Show that the local_intersect function for a cube correctly identifies intersections on any face.
This test creates a single cube and then casts a ray at each of its faces to show that the algorithm works correctly from all six directions.
| | Scenario Outline: A ray intersects a cube |
| | Given c ← cube() |
| | And r ← ray(<origin>, <direction>) |
| | When xs ← local_intersect(c, r) |
| | Then xs.count = 2 |
| | And xs[0].t = <t1> |
| | And xs[1].t = <t2> |
| | |
| | Examples: |
| | | | origin | direction | t1 | t2 | |
| | | +x | point(5, 0.5, 0) | vector(-1, 0, 0) | 4 | 6 | |
| | | -x | point(-5, 0.5, 0) | vector(1, 0, 0) | 4 | 6 | |
| | | +y | point(0.5, 5, 0) | vector(0, -1, 0) | 4 | 6 | |
| | | -y | point(0.5, -5, 0) | vector(0, 1, 0) | 4 | 6 | |
| | | +z | point(0.5, 0, 5) | vector(0, 0, -1) | 4 | 6 | |
| | | -z | point(0.5, 0, -5) | vector(0, 0, 1) | 4 | 6 | |
| | | inside | point(0, 0.5, 0) | vector(0, 0, 1) | -1 | 1 | |
The test also casts a ray from inside the cube, to show that the algorithm handles that case as well.
This works by treating a cube as it were composed of six planes, one for each face of the cube. Intersecting a ray with that cube involves testing it against each of the planes, and if the ray intersects them in just the right way, it means that the ray intersects the cube, as well. Let’s consider the algorithm at a simpler level, first, to build some intuition about how it works. Start by looking at the following figure. It shows a ray intersecting a 2D square.
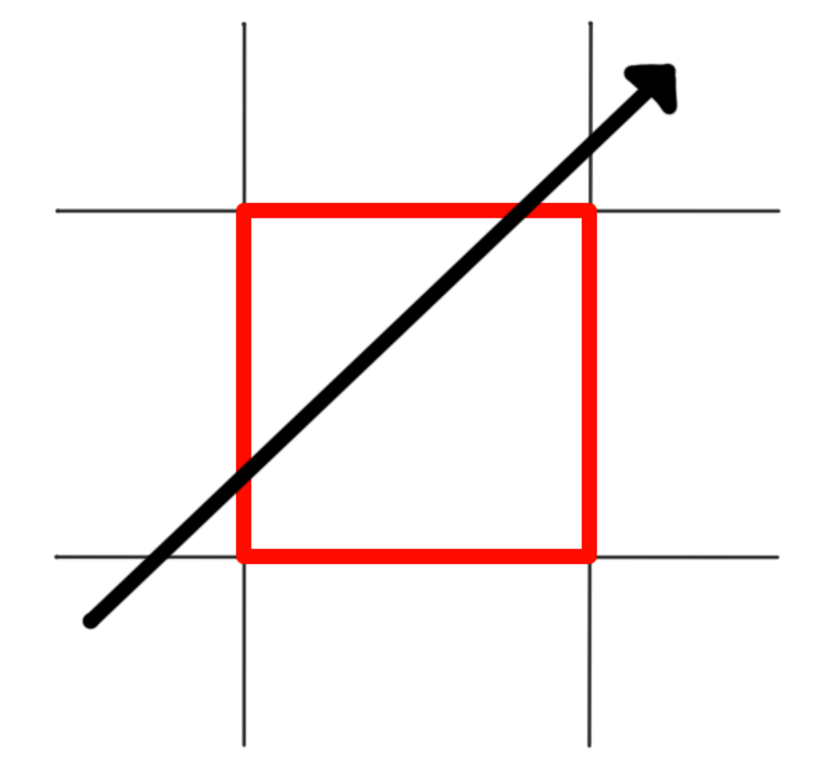
The first step is to find the t values of all the places where the ray intersects those lines, like this:
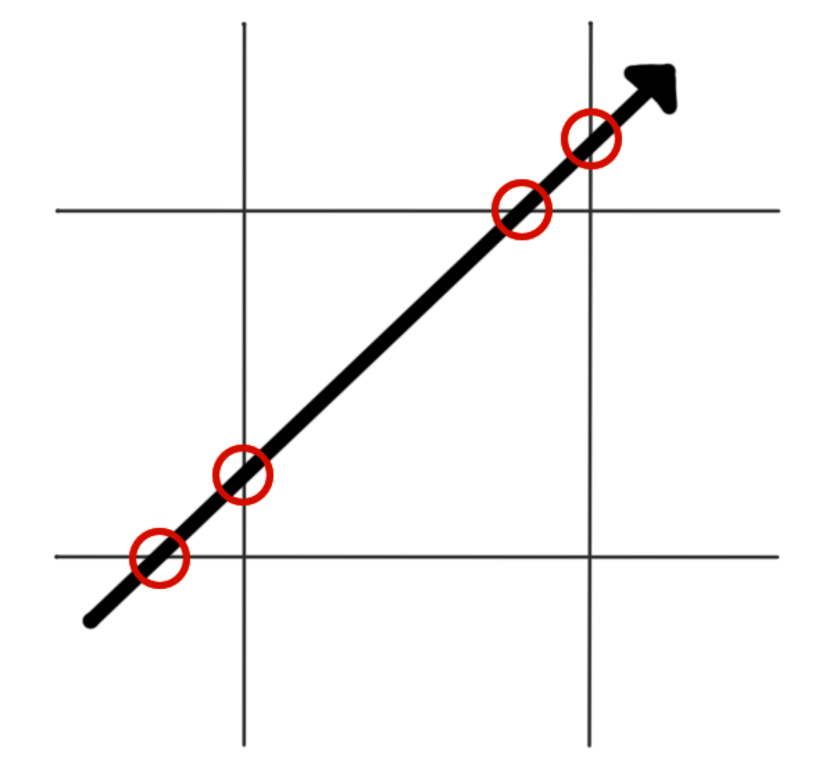
Next, consider them in parallel pairs. The following figure highlights the pairings with two blue intersections on two parallel blue lines, and two yellow intersections on two parallel yellow lines:
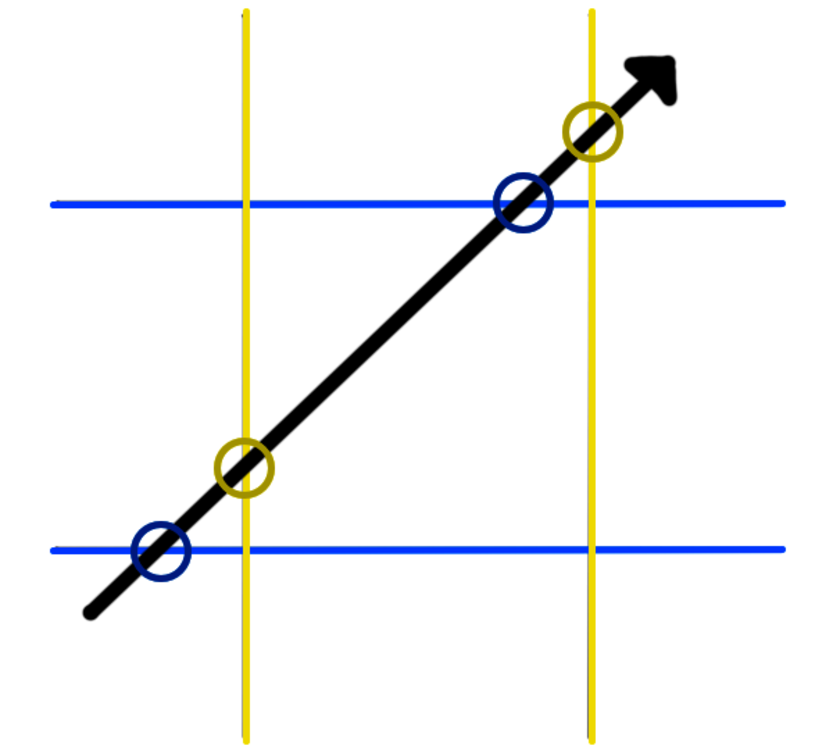
For each pair of lines, there will be a minimum t closest to the ray origin, and a maximum t farther away. Focus on the largest of all the minimum t values and the smallest of all the maximum t values, like so:

The intersection of the ray with that square will always be those two points: the largest minimum t value and the smallest maximum t value. This works for any number of dimensions, too. In three dimensions, you intersect planes instead of lines, but you still consider them in parallel pairs.
In pseudocode, the intersection routine itself looks like this:
| | function local_intersect(cube, ray) |
| | xtmin, xtmax ← check_axis(ray.origin.x, ray.direction.x) |
| | ytmin, ytmax ← check_axis(ray.origin.y, ray.direction.y) |
| | ztmin, ztmax ← check_axis(ray.origin.z, ray.direction.z) |
| | |
| | tmin ← max(xtmin, ytmin, ztmin) |
| | tmax ← min(xtmax, ytmax, ztmax) |
| | |
| | return ( intersection(tmin, cube), intersection(tmax, cube) ) |
| | end function |
For each of the x, y, and z axes, you’ll check to see where the ray intersects the corresponding planes and return the minimum and maximum t values for each. Once you’ve found those points of intersection, you find the actual points of intersection by taking the largest of the minimum t values and the smallest of the maximum t values.
The helper function, check_axis, looks like this in pseudocode:
| | function check_axis(origin, direction) |
| | tmin_numerator = (-1 - origin) |
| | tmax_numerator = (1 - origin) |
| | |
| | if abs(direction) >= EPSILON |
| | tmin ← tmin_numerator / direction |
| | tmax ← tmax_numerator / direction |
| | else |
| | tmin ← tmin_numerator * INFINITY |
| | tmax ← tmax_numerator * INFINITY |
| | end if |
| | |
| | if tmin > tmax then swap(tmin, tmax) |
| | |
| | return tmin, tmax |
| | end function |
This takes the ray-plane intersection formula that you used in Chapter 9, Planes, and generalizes it to support planes that are offset from the origin. Specifically, each pair of planes is offset 1 unit in opposing directions, hence -1 - origin and 1 - origin.
If the denominator (direction) is effectively zero, though, you don’t want to be dividing by it. The previous pseudocode handles this case by multiplying the numerators by infinity, which makes sure tmin and tmax—while both being infinity—have the correct sign (positive or negative).
|
|
If your programming language natively handles infinity and floating-point division by zero, you can avoid most of the song and dance in check_axis and just divide the numerators by the denominator. No special case needed when direction is zero! |
Implement this, and make that first test pass. Once you’ve got it working, move on to the next test!
Test #2: A Ray Misses a Cube
Show that the local_intersect function for a cube handles the case where the ray misses the cube.
Once again, the test creates a single cube, but this time the rays are cast in such a way that they miss the cube. Some are cast parallel to different faces, others are just cast diagonally away from the cube.
| | Scenario Outline: A ray misses a cube |
| | Given c ← cube() |
| | And r ← ray(<origin>, <direction>) |
| | When xs ← local_intersect(c, r) |
| | Then xs.count = 0 |
| | |
| | Examples: |
| | | origin | direction | |
| | | point(-2, 0, 0) | vector(0.2673, 0.5345, 0.8018) | |
| | | point(0, -2, 0) | vector(0.8018, 0.2673, 0.5345) | |
| | | point(0, 0, -2) | vector(0.5345, 0.8018, 0.2673) | |
| | | point(2, 0, 2) | vector(0, 0, -1) | |
| | | point(0, 2, 2) | vector(0, -1, 0) | |
| | | point(2, 2, 0) | vector(-1, 0, 0) | |
In each case, though, the ray should miss the cube, resulting in zero intersections.
Consider it from a two-dimensional perspective again. In the following configuration, the ray misses the square:
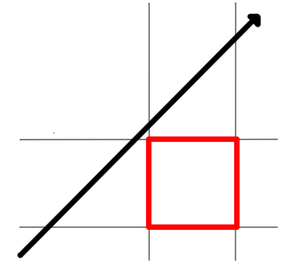
Once again, find the points of intersection with the two pairs of lines, and then find the largest of the minimum t values and the smallest of the maximum t values, like this:
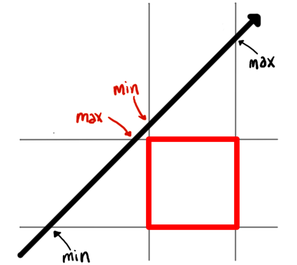
Look closely: the minimum t is farther from the ray origin than the maximum t! Well, that clearly makes no sense, and the contradiction is your clue that the ray misses the square.
The following pseudocode adds one line to the previous implementation, testing for that case.
| | function local_intersect(cube, ray) |
| | xtmin, xtmax ← check_axis(ray.origin.x, ray.direction.x) |
| | ytmin, ytmax ← check_axis(ray.origin.y, ray.direction.y) |
| | ztmin, ztmax ← check_axis(ray.origin.z, ray.direction.z) |
| | |
| | tmin ← max(xtmin, ytmin, ztmin) |
| | tmax ← min(xtmax, ytmax, ztmax) |
| | |
| » | return () if tmin > tmax |
| | |
| | return ( intersection(tmin, cube), intersection(tmax, cube) ) |
| | end function |
Once you’ve got that test passing, you’re ready to implement the last bit for cubes: calculating the normal vector.
