9
How Aging Laws Influence Parametric and Catastrophic Reliability Distributions
9.1 Physics of Failure Influence on Reliability Distributions
Reliability distributions are actually designed to fit regions of the bathtub curve shown in Figure 9.1. An overview of key reliability statistics is provided in Special Topics A to aid the reader.
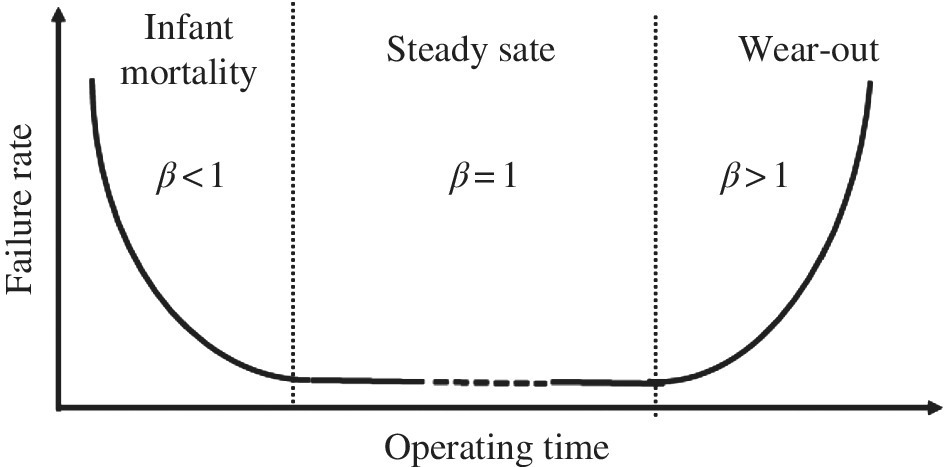
Figure 9.1 Reliability bathtub curve model
For example, the Weibull distribution is basically a power law over time (see Special Topics A.4.2). If we were to invent a distribution based on wear-out for example, we might use a failure rate λ(t) proportional to time raised to a power >1. For example, wear-out on a particular device may fit a power law with time squared as (Figure 9.2)
Figure 9.2 Power law fit to the wear-out portion of the bathtub curve
This is essentially a Weibull failure rate, although the actual Weibull failure rate is written in a more sophisticated way as (see Special Topics A.4.2):
This is still a power law and, in this case, β would equate to 3. Note α is the characteristic life. Many reliability engineers tend to favor the Weibull distribution because of the physical significance of the β parameter. That is, the power exponent in the distribution helps to determine the portion of the bathtub curve that we are in. If we fit our life test data to the Weibull model and β = 1, our data appear to be in the steady-state portion of the bathtub curve; β > 1 indicates wear-out; and β < 1 indicates infant mortality as shown in Figure 9.1. Often semiconductor engineers work with the lognormal distribution [1,2].
True statisticians will likely tell you that whichever distribution fits the data best will provide the most accurate assessment. However, we might ask a deeper question: what is the physics of failure influencing the failure rate distribution? In this chapter we will examine how the physics of the aging laws influence reliability distributions. Perhaps if we have a reason to use a particular distribution, from a physics standpoint, it might influence our decision on how we analyze our data. Aging laws have parameters. Therefore, our initial discussion will revolve around parametric reliability distributions. Once these are established we can often infer how the catastrophic distribution will follow.
9.2 Log Time Aging (or Power Aging Laws) and the Lognormal Distribution
We know from production that parameters tend to be normally distributed. For example, we can measure the strength distribution of say Young’s modulus on numerous metal parts of the same type. The modulus will of course not all be exactly the same on each part, but will vary with metallurgical issues and geometric and assembly variations. That said, they are likely to be normally distributed (see Special Topics A.4.3). Now we might note that we have described physical phenomenon such as creep with the thermally activated time-dependent (TAT) model as having a log-time aging form.
We would like to illustrate that if parts are normally distributed and age in log-time, then their failure rate is lognormal (see Special Topics A.4.4). Furthermore, since we have demonstrated that power laws (such as that shown in Equation (9.3)) where the aging exponent for time K is between 0 and 1 can also be modeled as aging in log-time (see Figure 6.3), this can also apply to power laws that may be better described by log-time aging.
To that end, the general form of the TAT model is (see Equation (6.7)):
and to simplify, when bt >> 1 we can write
Here P is the parameter of interest, such as creep, beta transistor aging, or perhaps crystal frequency drift, and so forth.
In order to have parametric failure, one needs a definition for failure. To this end it is customary to define a parametric failure threshold. That is, when a component ages, one of its key parameters drifts out of specification. This value can be used as the failure threshold. For example, transistor degradation in power loss is often taken as a loss of 10 or 20% of the original value. The figure below depicts a key parameter reaching a failure threshold of P = 1.37 at time t = 3. Here time units are not defined but are usually in hours or months and so forth (Figure 9.3).
Figure 9.3 Log time aging with parametric threshold tf
When manufactured parts are normally distributed, a parameter of interest can be statistically assessed using Gaussian probability density function (PDF) (Special Topics A.4.3):
where p is the parameter of interest. Now consider that the parameter is aging according to a log-time equation such as Equation (9.3); its time dependence must then be lognormally distributed, that is, we have from Equations (9.4) and (9.5):
where for purposes of illustration in Equation (9.4) we have let A = b = 1 (Figure 9.4).
Figure 9.4 PDF failure portion that drifted past the parametric threshold
It is customary to change variables so that we may formally obtain the lognormal distribution for the above equation, then
With this change of variables we can now write
where the function f(t:t50,σ) is the lognormal PDF (see Special Topics A.4.4).
Reliability life test data is plotted using a function related to the PDF, called the cumulative distribution function (CDF) F(t). They are related as
The CDF for the lognormal distribution can be written in closed form with the help of the error function (erf) as
Often, one writes the lognormal mean as
and the dispersion is assessed graphically as
Thus, the physical implications can be related to log-time aging similar to a TAT model described in Chapters 6 and 7.
When a manufactured part has a key parameter that is distributed normally and ages in log-time (see Figure 9.4), its failure rate is generally lognormally distributed [2,3]. This is likely the case for power-law aging models as well as when the power 0 < k < 1 in Equation (9.3).
Although we have described this for parametric failure, it can be argued that many catastrophic failure mechanisms dominated by log-time aging will also fall into this category. For example, if a transistor is aging most of its lifetime in log-time then suddenly fails catastrophically due to an underling log-time aging mechanism such as gate leakage (see Section 7.4.1), then the transistor’s failure distribution is likely lognormal. The parametric threshold in this case resulted in a true catastrophic failure event with most of its lifetime aging logarithmically in time.
We exemplify with the TAT model, writing an aging parameter P in log-time aging form:
where the approximation is for bt >> 1; 
are average values; and 
and ln(t50) is the mean of [ln(t)] failure time. Then Equation (9.8) for the parametric PDF becomes
The CDF is then
9.3 Aging Power Laws and the Weibull Distribution: Influence on Beta
Most parametric aging laws have a power-law dependence. Consider creep as an example:
where Δε is the creep strain; t is time; and a and n are constants of the creep model [4]. This simple equation can actually model both the primary and secondary creep phases, as well as roughly the third-stage tertiary creep phase as shown in Figure 9.5.
Figure 9.5 Creep curve with all three stages
Now we would like to provide some new understanding of the Weibull distribution, how underlying aging laws might influence the distribution, or how analysis might help us in determining an aging law (not found in other books). As a point of reference, we write the popular Weibull failure rate as (Special Topics A.4.2)
For the traditional Weibull model, β < 1 is infant mortality; β = 1 is steady state; and β > 1 is wear-out.
There are traditional functions to help obtain the failure rate in reliability statistics. The functional definition for the instantaneous failure rate is defined with
where R(t) is the reliability function, f(t) is the PDF, and F(t) is the CDF.
However, for what we wish to do we are going to start off with a simplified definition for the average expected failure rate as:
where ΔE is the expected fractional units that fail in the time interval Δt. Then in the limit as Δ becomes infinitesimally small, we write the failure rate as
Let’s now look at an oversimplified parametric aging power law form for the three stages of creep (see Equation (4.13) for a more detail model)
There are numerous time-dependent creep models that are commonly used that have more complex forms and are better suited to model creep. For example, in Equation (4.13) have seen that ε0 = Aσb indicating different stresses affect the creep slope (see Figure 9.6). This particular model is oversimplified, but it is roughly capable of modeling all three stages of creep shown in Figure 9.5. This oversimplified power-law form is very instructional as there are numerous similar power aging laws of this type in physics of failure applications. The three stages of creep are shown in Figure 9.5.
Figure 9.6 Creep rate power law model for each creep stage, similar to the bathtub curve in Figure 9.1
When 0 < N < 1 it models Primary Stage 1; when N = 1 it models Secondary Stage 2; and when N > 1 it models Tertiary Stage 3. The creep rate is defined
Now using the different power-law values for creep, we can plot the creep rate curve as shown in Figure 9.6. Interestingly enough, the bathtub curve in Figure 9.1 has a similar shape to the creep rate curve shown in Figure 9.6. Note that Stage 2, although not flat like the idealized bathtub curve, there are some situations reported that this steady-state area of the bathtub curve has a small increasing failure rate.
What we are therefore tempted to do is try and merge the physics of creep to the statistical failure rate equations and make inferences. Although it is seemingly discomfited, we will see that it is insightful.
Let us start by saying that for any creep phase, we can have a parametric failure corresponding to the parametric failure threshold tfailure so that the time to failure in general will be given by
where we assume the following parametric treatment. For example, in testing when a device passes the failure threshold Δεfailure, corresponding to a time tfailure, we count the device as a failure and proceed to perform some sort of traditional reliability catastrophic type of analysis to find its failure distribution and failure rate based on the time to failure for each device that passes the creep threshold. We have no idea of the life test parametric distribution, however. If it were normal for example, we would have a mean time to failure and a spread in the times to failure given by sigma.
However, in this discussion we would like to proceed and make inferences from the aging law on how it influences the statistics. The expected fraction of devices that will fail ΔE (Δεfailure(t)) in the time interval Δt then must be a function of the aging law so that the failure rate as we have defined it above is
where we have let
If we assume a Weibull distribution for the parametric failure rate, we can make some observations. By direct comparison to the traditional Weibull parameters between Equations (9.17) and (9.24), we conclude
So in this model if 0 < N < 1, say 
, indicating that creep is in the Primary Creep Stage 1, then we are also in the infant mortality region. This is reasonable as it indicates early failure. If N = 1, then we have a constant creep rate which is in the Secondary Creep Stage 2. This is also associated with the steady-state region of the bathtub curve as 
. Finally, if 
, we reach the Tertiary Creep Stage 3 and are in the wear-out phase of the bathtub curve. Therefore, the physics for creep rate matches the statistics reasonably well.
Essentially we have made direct comparisons between the creep rate in Figure 9.6 and the failure rate in Figure 9.1, finding that N ~ β. It is therefore likely that for numerous aging power laws, when carefully modeled, the power exponent, can be directly tied to the value of the Weibull β. We have now connected both the Weibull model and the lognormal model for physical aging laws.
In catastrophic analysis, it is customary to assign α to a value of the aging equation, for example
This is a number so we can just keep it in mind. It is evaluated at the failure time for parametric failure.
This now begs the question, when we do a Weibull catastrophic failure analysis (i.e., hard failure as compared to soft parametric failure) and find the parameters α and β, is there an underlying aging law of the form in Equation (9.23) that we can associate with the Weibull parameters?
It is likely that there is not a perfect answer for this question. First it would require a simplified aging law similar to Equation (9.23). Then it requires that the dominant part of a product’s lifetime was due to parametric well-behaved failure that can be modeled by the aging power law. Lastly, the catastrophic failure event would be fairly abrupt so that the aging law is a good approximation of the lifetime. That being said, it is still best to do a multivariable Weibull analysis so the parameters N, β, and α can be found from the failure analysis.
9.4 Stress and Life Distributions
It is instructive to illustrate how to incorporate a stress model into a life distribution. We have done this already from first principals. However, we would like to illustrate it for commonly used time-to-failure stress equations. We will illustrate this for both the power law form and the Arrhenius function and how these are incorporated into the CDF and PDF for the lognormal distribution (Figure 9.7).
Figure 9.7 Creep strain over time for different stresses where σ4 > σ3 > σ2 > σ1
Consider the vibration stress causing creep or fatigue (σ(W)) and the Arrhenius temperature time to failure model given earlier in Equations (4.46) and (5.22), respectively. The time to failure is written in linear form as
Then for a vibration stress we would consider Equations (4.38) and (4.46) in linear form
where Mb = –(b/2) ln(β/f) (Equation (4.46)).
Experimentally, the time to failure can be assessed at any time. For the lognormal distribution, these parameters apply to the median time to failure, tfailure = t50. This allows for a direct substitution into the lognormal distribution functions of Figures A.8 and A.9. Inserting the Arrhenius function into the PDF gives us
For the vibration model, this is
Similarly, inserting the Arrhenius model into the CDF (using the erf form in Equation (A.23)) yields
For the vibration model, this is
Similar expressions can be found for the CDF and PDF of any life distribution function when tfailure is appropriately found [2]. As an exercise, the reader might wish to apply this methodology for the Weibull CDF and PDF. (Hint: assume that t0.632 = tfailure; this is the characteristic life αw in the table.)
9.4.1 Example 9.1: Cumulative Distribution Function as a Function of Stress
For the vibration function, let C = −7.82, Mb = 4, and find F(t,W) for t = 10 years and W = 0.0082 G2/Hz. Find F at 10 years. Use σ = 2.2 for your estimate. If the stress level is reduced by a factor of 2, what is F?
Solution
Inserting these values into the CDF above gives us
or
Thus, at this stress level, 49.7% of the distribution is anticipated to have failed in 10 years. (Note that in the above derivation the erf values can be found from tables or in Microsoft Excel type “erf(0.00447)” to obtain the above value.) If the stress level is reduced by a factor of 2, then W = 0.0041 G2/Hz. The anticipated percent failure at 10 years is reduced to F(87 600, 0.0041)= 10.27%.
9.5 Time- (or Stress-) Dependent Standard Deviation
Most models assume that β for the Weibull or σ for the normal or lognormal distributions are independent of time and/or stress. This may not always be the case, especially in parametric analysis. Figure 9.8 illustrates parametric crystal frequency drift of a distribution of oscillators tested at 120°C [3]. This type of plot is a cumulative probability plot versus frequency. Each fitted line shows the observed mean and standard deviation observed at 400, 600, and 1000 h. The slope of each time group leads to the standard deviation; as can be seen, it varies greatly.
Figure 9.8 Crystal frequency drift showing time-dependent standard deviation.
Source: Feinberg [3]. Reproduced with permission of IEEE
Such parametric dependence leads to a time dependence on sigma and likely also in the catastrophic case for crystal oscillator frequency drift. Usually, there is not enough data to determine this dependence and σ is treated as a constant over time and/or stress.
The simplest way to model a time or stress-dependent standard deviation from the data such as those shown in Figure 9.8 is to first determine the standard deviation for each distribution. This is usually given in the software but can also be easily read off the graph, for example at 400 h we have
Once we have the standard deviation for each distribution over time, that is, σ(400), σ(600), σ(1000) at times t = 400, t = 600, and t = 1000 h, we can then plot σ versus time on a graph and establish the relationship by fitting this data. For example, if it is linear then a likely model would lead to a straight line fit for these points as [2]
If σ is stress dependent, we can follow the same procedure. We can also do this for a Weibull distribution if the data show, for example, that β is stress or time dependent.
References
- [1] O’Connor, P. and Kleyner, A. (2012) Practical Reliability Engineering, 5th edn, John Wiley & Sons Ltd, London.
- [2] Feinberg, A. and Crow, D. (eds) Design for Reliability. M/A-COM 2000. CRC Press, Boca Raton, 2001.
- [3] Feinberg, A. (1992) Gaussian parametric failure rate model with applications to quartz-crystal device aging. IEEE Transaction on Reliability, 41, 565.
- [4] Collins, J.A., Busby, H. and Staab, G. (2010) Mechanical Design of Machine Elements and Machines, 2nd edn, John Wiley & Sons, Inc., New York.