Keywords

Die-to-die variations; within-die variations; process variability in 3-D circuits; clock skew variations; power supply noise in 3-D circuits; skitter

17.1 Process Variations in Data paths Within Three-Dimensional ICs

Interestingly, variability in 3-D circuits has to date not been adequately investigated. The multi-tier nature of these circuits requires different statistical models to account for process variations. To exemplify this requirement, consider the datapaths illustrated in Fig. 17.2. For the datapath shown in Fig. 17.2A, one random variable can be used for each gate to describe the effects of WID variations on the delay of this gate. Furthermore, one random variable, common for all of the gates along the path, is used to capture the effect of D2D variations. Thus, a statistical model that describes the delay distribution of this path requires seven random variables.

Alternatively, for the path shown in Fig. 17.2B, which spans two physical tiers, the situation is somewhat different. The same number of random variables is required to model WID variations. Two variables are, however, needed to model D2D variations as some gates along the path are placed in another tier. Assuming that these tiers originate from different wafers (a reasonable assumption for the vast majority of systems), these variables should be modeled as independent. Furthermore, if all of the tiers are fabricated with the same process (e.g., a memory stack), these random variables are also considered to be identically distributed. Alternatively, this situation is not the same if a different process is used for all or some of the tiers. The former case is assumed in this chapter to model the multiple sources of D2D variations that can exist within a 3-D stack. The effects of multiple D2D variations on the speed of datapaths in a 3-D circuit are described in [632]. This work constitutes the basis of this section.

A statistical delay model for 3-D circuits is based on the critical path model described in [633]. This path model describes the performance of a datapath while hiding information from the lower abstraction levels. Although this approach adds some inaccuracy, a general path model is useful in adding insight into the effects of variability on the performance of 3-D circuits. Note that the general critical path model in [633] is for planar circuits. The model utilizes two primary parameters, the number of critical paths within a circuit N_cp and the number of stages within each critical path n_cp. Another assumption of the model is that all of the n_cp stages within a critical path are two input NAND gates.

To model D2D variations, a single random variable G is employed for all of the gates, while the effects of WID variations are modeled by a set of independent and identically distributed random variables notated as L_ij, where 1≤i≤N_cp and 1≤j≤n_cp. Consequently, L_ij describes the effects of WID variations on gate j of path i. Based on this notation, the maximum delay variation due to the combined effect of D2D and WID variations is [633]

$\mathrm{\Delta }{T}_{\max }^{2-D}=\underset{1\le i\le N_{\mathit{cp}}}{\max }(\sum _{j=1}^{n_{\mathit{cp}}}a\left(G+L_{\mathit{ij}}\right))=\underset{1\le i\le N_{\mathit{cp}}}{\max }\left(n_{\mathit{cp}}\mathit{aG}+\sum _{j=1}^{n_{\mathit{cp}}}a{L}_{\mathit{ij}}\right),$ (17.1)

(17.1)

where a is the sensitivity of the delay of the gates to process variations. Using the common assumption that both D2D and WID process variations follow a normal distribution, that is G~N(0, σ_G) and L~N(0, σ_L), the probability that the maximum delay variation of the critical paths is less than a specific delay τ is

$\mathit{Pr}\left\{\mathrm{\Delta }{T}_{\max }^{2-D}\le \tau \right\}=F_{{\mathrm{\Delta }\mathrm{T}}_{\max }^{2-D}}\left(\tau \right)=f_G\left(\frac{\tau }{\alpha n_{\mathit{cp}}}\right)*\left({F_L\left(\frac{\tau }{\alpha \sqrt{n_{\mathit{cp}}}}\right)}^{N_{\mathit{cp}}}\right).$ (17.2)

(17.2)

The functions f_K() and F_K() are, respectively, the probability density function and the cumulative density function (cdf) of the random variable K and the sign * corresponds to the convolution operation.

The primary difference in the modeling procedure for delay variations in 3-D circuits is that a single variable G to describe D2D variations can no longer be used. This situation is due to the existence of intertier paths, as depicted in Fig. 17.2. Consequently, if a 3-D circuit includes m tiers, m random variables are required to model D2D variations. Based on the discussion of intra and intertier paths, the number of intertier and intratier critical paths within a 3-D circuit are, respectively, notated as $N_{\mathit{cp}}^{\mathrm{inter}}$ and $N_{\mathit{cp}}^{\mathrm{intra}}$. If tier i contains $N_{\mathit{cp}}^i$ intratier paths, the total number of intratier paths throughout a 3-D stack is

$N_{\mathit{cp}}^{\mathrm{intra}}=\sum _{i=1}^m{N}_{\mathit{cp}}^i.$ (17.3)

(17.3)

Accordingly, the within each intratier path within any tier of a 3-D circuit is assumed to comprise $n_{\mathit{cp}}^{\mathrm{intra}}$ number of stages. Similarly, the number of stages of an intertier path is notated as $n_{\mathit{cp}}^{\mathrm{inter}}$, where the number of gates within this path placed in each tier i is denoted by $n_{\mathit{cp}}^i$. Based on this notation,

$n_{\mathit{cp}}^{\mathrm{inter}}=\sum _{i=1}^m{n}_{\mathit{cp}}^i.$ (17.4)

(17.4)

To better understand this notation, an example of a two-dimensional (2-D) and 3-D circuit is shown in Fig. 17.3. For the 2-D circuit depicted in Fig. 17.3A, $N_{\mathit{cp}}=2$ and $n_{\mathit{cp}}=3$ for both paths. Alternatively, in Fig. 17.3B, there is one intertier and two intratier paths, which, respectively, means that $N_{\mathit{cp}}^{\mathrm{intra}}=2$ and $N_{\mathit{cp}}^{\mathrm{inter}}=1$. For the intratier paths, $n_{\mathit{cp}}^{\mathrm{intra}}=3$, while for the intertier path, $n_{\mathit{cp}}^1=1$ and $n_{\mathit{cp}}^2=2$. Another distinction in the notation of WID random variables is shown in Fig. 17.3, where the variables for the WID variations of the intratier paths are notated as L_ij and the variables for the WID variations of the intertier paths are notated as L’_ij, capturing the delay variation of gate j in the (intra or intertier) critical path j. In a manner similar to (17.1), the delay variation of a critical path i within a multi-tier circuit for the intratier paths [632] is

$\mathrm{\Delta }{T}_i^{\mathrm{intra}}=n_{\mathit{cp}}^{\mathrm{intra}}a{G}_{g(i)}+\left(\sum _{j=1}^{n_{\mathit{cp}}^{\mathrm{intra}}}a{L}_{\mathit{ij}}\right),1\le i\le N_{\mathit{cp}}^{\mathrm{intra}},$ (17.5)

(17.5)

and for the intertier paths [632] is

$\mathrm{\Delta }{T}_i^{\mathrm{inter}}=\left(\sum _{j=1}^m\beta n_{\mathit{cp}}^j{G}_j\right)+\left(\sum _{j=1}^{n_{\mathit{cp}}^{\mathrm{inter}}}\beta L_{\mathit{ij}}^{\prime }\right),1\le i\le N_{\mathit{cp}}^{\mathrm{inter}},$ (17.6)

(17.6)

where g() is a mapping function that projects each intratier critical path onto one of the m tiers. The sensitivity of the gate delay to process variations for intra and intertier paths is, respectively, denoted by α and β. The maximum delay variation for the entire 3-D circuit is the maximum delay variation provided by (17.5) and (17.6),

$\mathrm{\Delta }{T}_{\max }^{3-D}=\underset{1\le i\le N_{\mathit{cp}}^{\mathrm{intra}},1\le j\le N_{\mathit{cp}}^{\mathrm{inter}}}{\max }\left(\mathrm{\Delta }{T}_i^{\mathrm{intra}},\mathrm{\Delta }{T}_j^{\mathrm{inter}}\right).$ (17.7)

(17.7)

Determining a closed-form expression for (17.7) is a complicated task. This intractability is due to the intertier paths [632]. Consequently, upper and lower bounds (LBs) are determined for (17.7), while for the delay variation of intratier paths, closed-form expressions are similar to (17.1). Note that in (17.5) a mapping function exists for each intratier path to another tier within the stack. Assuming that the intratier paths are divided equally among the m tiers of the stack, the cumulative distribution function (cdf) for the intratier paths in a 3-D circuit is

$F_{{\mathrm{\Delta }\mathrm{T}}_{\max }^{3-D}}\left(\tau \right)={\left[f_G\left(\frac{\tau }{\alpha n_{\mathit{cp}}^{\mathrm{intra}}}\right)*\left({F_L\left(\frac{\tau }{\alpha \sqrt{n_{\mathit{cp}}^{\mathrm{intra}}}}\right)}^{\frac{N_{\mathit{cp}}^{\mathrm{intra}}}{m}}\right)\right]}^m,$ (17.8)

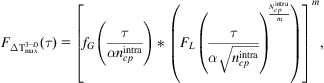(17.8)

where * is the convolution operation. Different from a 2-D circuit the number of tiers affects the cdf, as described by (17.8). Furthermore, the critical paths are assumed to be equally split among the tiers of the stack. This mapping yields the worst case delay variability for the intratier paths [632]. These results suggest that to better manage variability in 3-D circuits, process aware physical design should carefully consider the distribution of the paths among the tiers within a stack.

Based on these analytic formulations, another conclusion is that a planar circuit has a higher likelihood to satisfy a timing constraint as compared to a 3-D circuit. The related assumptions are that both circuits contain the same number of critical paths, and that the 3-D circuit does not contain any intertier paths. Although this last assumption is rather restrictive, assuming that registers are present at the boundary of each tier for intertier nets, this argument demonstrates that process variability is an important issue for 3-D circuits, a situation that has to date been neglected. To exemplify these results, consider Fig. 17.4 where the cdf of different circuits with the same critical paths are considered. These curves demonstrate that a 2-D circuit exhibits a higher probability to satisfy a timing constraint (τ) as compared to a 3-D version of the same circuit. Moreover, a 3-D circuit with an even distribution of paths between the two tiers is the least likely circuit to satisfy a design constraint. Note that these results do not consider any changes that the third dimension brings into the physical design of the circuit.

To provide a complete picture of the importance of process variations on datapaths within 3-D circuits an intertier path is considered. In this case, however, the delay variation cannot be described analytically and only bounds are provided [632]. The LB is set to the greatest delay variation of the intratier paths,

$\mathrm{\Delta }{T}_{\max }^{\mathrm{LB}}=\underset{1\le i\le N_{\mathit{cp}}^{\mathrm{intra}}}{\max }(\mathrm{\Delta }{T}_i^{\mathrm{intra}}).$ (17.9)

(17.9)

Although this approach appears as a crude simplification, the bound in (17.9) is not loose since the intertier path delay is determined by adding the random variables for the D2D variations. This summation decreases the standard deviation of an intertier path as compared to an intratier path. Assuming therefore that all of the traits of intra and intertier paths are the same (e.g., the number of gate stages and sensitivity of each gate delay to process variations), an intertier path always exhibits a lower likelihood to limit the performance of a 3-D circuit.

Alternatively, the upper bound (UB) can be described by [632]

$\mathrm{\Delta }{T}_{\max }^{\mathrm{UB}}=\max (\underset{i}{\max }(\mathrm{\Delta }{T}_i^{\mathrm{intra}}),\underset{i}{\max }(\mathrm{\Delta }{T}_i^{\mathrm{inter},\mathrm{UB}})),$ (17.10)

(17.10)

where

$\mathrm{\Delta }{T}_i^{\mathrm{inter},\mathrm{UB}}=\sum _{j=1}^m\beta n_{\mathit{cp}}^j{G}_j^{\prime }+\sum _{j=1}^{n_{\mathit{cp}}^{\mathrm{D}2\mathrm{D}}}\beta L_{\mathit{ij}}^{\prime }.$ (17.11)

(17.11)

In this expression, a set of new random variables $G_j^{\prime }$ is introduced which are assumed to be independent and identically distributed as G_j. Based on (17.10) and (17.11), the cdf of $\mathrm{\Delta }{T}_{\max }^{\mathrm{UB}}$ becomes [632]

$F_{{\mathrm{\Delta }\mathrm{T}}_{\max }^{\mathrm{UB}}}\left(\tau \right)=\left[\prod _{i=1}^m{f}_G\left(\frac{\tau }{k_1}\right)*\left({F_L\left(\frac{\tau }{k_2}\right)}^{N_{\mathit{cp}}^i}\right)\right]\left[f_G\left(\frac{\tau }{k_3}\right)*\left({F_L\left(\frac{\tau }{k_4}\right)}^{N_{\mathit{cp}}^{\mathrm{inter}}}\right)\right],$ (17.12)

(17.12)

where $k_1=a{n}_{\mathit{cp}}^{\mathrm{intra}}$, $k_2=a\sqrt{n_{\mathit{cp}}^{\mathrm{intra}}}$, $k_3=\beta {\sum }_{i=1}^m{(n_{\mathit{cp}}^i)}^2$, $k_4=\beta \sqrt{n_{\mathit{cp}}^{\mathrm{inter}}}$.

The application of this model on synthetic critical paths for a 90 nm process node demonstrates interesting tradeoffs [632]. Assuming 1,000 critical paths, each consisting of six NAND gates, and introducing the parameter $\gamma ={\sigma }_G^2/{\sigma }_{\mathrm{tot}}^2$ to describe the importance of D2D variations (modeled as a random variable G) over the total variations, the mean of the maximum critical path delay is determined for different placements of the critical paths among the tiers within a 3-D system. The parameter γ has the values, 0.25, 0.5, and 0.75, where a higher γ corresponds to a greater contribution of D2D variations. Furthermore, the number of tiers changes from one (i.e., a 2-D circuit) to six tiers.

These results indicate that if only intratier paths are assumed, the mean delay increases by 9.5% for γ=0.5, while for lower γ, the increase in the mean delay is lower. If only intratier paths are assumed, the D2D variations affect all of the gates along the critical paths within a tier in the same way, shifting the nominal mean delay. If the contribution of D2D variations is greater than the total variations, this shift is more pronounced. Alternatively, WID variations affecting each gate (or stage) of the critical paths have an averaging effect for longer (multistage) paths [634], leading to a smaller shift in the mean delay. Consequently, if the D2D variations are low, the increase in the mean delay is also low.

The placement of the critical paths among the tiers of the 3-D stack also affects the mean delay, where an uneven distribution of the critical paths among the tiers produces higher yield [632]. Although this situation suggests the placement of the critical paths in those tiers where D2D variations are lower, other design constraints may not permit such a placement. However, including variability in the physical design process for 3-D circuits can reduce the performance margins of the circuits; particularly since overall variability in 3-D systems is expected to worsen as compared to 2-D circuits [632].

Alternatively, if the critical paths span more than one tier, meaning that both intra and intertier critical paths exist in a 3-D circuit, the delay distribution of these paths decreases. This behavior is similar to the averaging effect of WID variations in intratier paths. As the gates within the intertier paths are spread over several tiers, the contribution of D2D variations from different tiers can cancel each other, yielding a narrower delay distribution of the critical paths as compared to those 3-D circuits that are comprised of only intratier critical paths. The interplay between the contribution of WID and D2D variations is applied in the following section to the design of more robust global clock distribution networks for 3-D circuits, where a highly accurate variation aware clock skew model is also described.

17.2 Effects of Process Variations on Clock Paths

Several global 3-D clock distribution networks are presented in Chapter 15, Synchronization in Three-Dimensional ICs. In this section, the effects of process variations on the principal traits of 3-D clock networks, such as clock skew and power, are discussed. To consider these effects, effective statistical delay models are required to describe the distribution of the clock skew for disparate 3-D clock network topologies. A model of the delay distribution of a clock buffer including both WID and D2D variations is described in Section 17.2.1. This model produces a delay distribution of clock paths, as described in Section 17.2.2. This distribution is, in turn, utilized to describe the distribution of clock skew in 3-D clock trees, as discussed in Section 17.2.3. Based on these models, the effects of process variations on clock skew distribution for different clock networks are reviewed, and a robust 3-D clock topology is presented in Section 17.2.4.

17.2.1 Statistical Delay Model of Clock Buffers

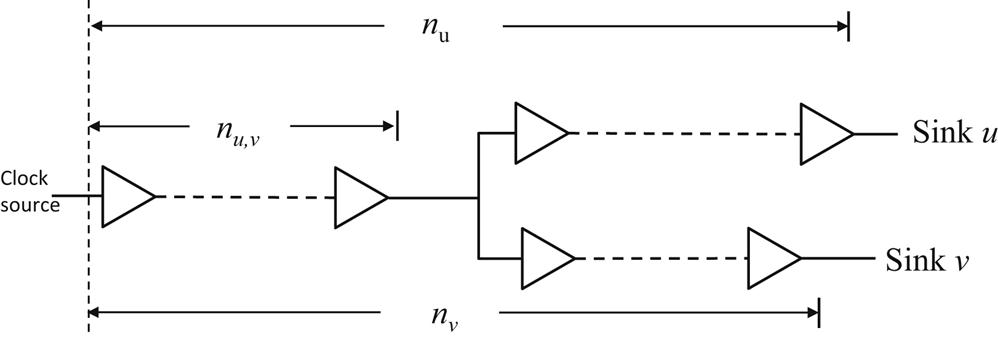
A typical buffered 3-D H-tree is illustrated in Fig. 17.5. The pairwise clock skew is defined as the skew between every pair of sinks in a 3-D clock distribution network, S_skew={s_i,j|s_i,j=D_i−D_j, 1≤i, j≤n_sink}. Sinks i and j can be located in any tier of the 3-D circuit. s_i,j denotes the skew between sinks i and j. The clock signal delay to sinks i and j is denoted, respectively, by D_i and D_j. The number of clock sinks is n_sink. To determine the distribution of skew S_skew for the clock sinks, a statistical delay model for a clock buffer is required.

The overall variation in the delay of a clock buffer is dependent on the variations of the input capacitance and output resistance [635,636]. This approach considers the input slew rate to more accurately model the distribution of the buffer delay. The interconnects constituting a clock stage are modeled as distributed RC wires. The circuit illustrated in Fig. 17.6 is utilized to obtain the variation of the buffer delay for different input signal slew rates.

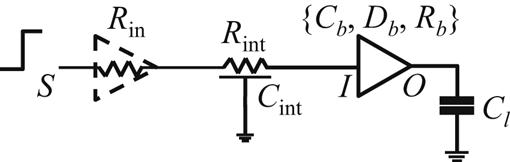
Let R_in denote the output resistance of a buffer driving a second buffer. The load capacitance of the buffer is denoted by C_l. Interconnects with diverse impedance characteristics are modeled by employing different R_int and C_int, where R_int and C_int denote, respectively, the resistance and capacitance of the interconnects. The interconnect R_int and C_int can also be adjusted to produce different slew rates for the input signal of the buffer shown in Fig. 17.6.

For a step input signal, the Elmore delay [414] from source S to nodes I and O (in Fig. 17.6) is, respectively,

$D_{\mathrm{SI}}=0.69R_{\mathrm{in}}{C}_{\mathrm{int}}+0.38R_{\mathrm{int}}{C}_{\mathrm{int}}+0.69\left(R_{\mathrm{in}}+R_{\mathrm{int}}\right)C_b,$ (17.13)

(17.13)

${\Delta D}_{\mathrm{SI}}=0.69\left(R_{\mathrm{in}}+R_{\mathrm{int}}\right){\Delta C}_b,$ (17.14)

(17.14)

$D_{\mathrm{SO}}=D_{\mathrm{SI}}+D_b+0.69R_b{C}_l,$ (17.15)

(17.15)

${\Delta D}_{\mathrm{SO}}={\Delta D}_{\mathrm{SI}}+{\Delta D}_b+0.69{\Delta R}_b{C}_l,$ (17.16)

(17.16)

where C_b, R_b, and D_b are, respectively, the input capacitance, output resistance, and intrinsic delay of the buffer. Variations of C_b, R_b, and D_b are, respectively, denoted by ΔC_b, ΔR_b, and ΔD_b. For the buffer shown in Fig. 17.6, R_in is considered constant (for the moment).

Through several Monte Carlo simulations, the delay variation at nodes I and O is measured by setting C_l to zero (corresponding to ${\Delta D}_{{\mathrm{SO}}_0}$) and a different value (e.g., 200 fF, corresponding to ${\Delta D}_{{\mathrm{SO}}_1}$). The mean value and standard deviation of ΔC_b, ΔR_b, and ΔD_b are obtained from (17.14) and (17.16) [636]. Assuming that process variations can be described by a Gaussian distribution, the electrical characteristics of a buffer can also be approximated by a Gaussian distribution [637],

${\Delta C}_b\mathcal{~}\mathcal{N}\left(0,{\sigma }_{C_b}^2\right),{\Delta R}_b\mathcal{~}\mathcal{N}\left(0,{\sigma }_{R_b}^2\right),{\Delta D}_b\mathcal{~}\mathcal{N}\left(0,{\sigma }_{D_b}^2\right).$ (17.17)

(17.17)

${\sigma }_{C_b}$ is characterized from (17.14). According to (17.14) and (17.16), ${\sigma }_{D_{\mathit{SO}}}$ is dependent on ${\sigma }_{C_b}$, ${\sigma }_{D_b}$, and ${\sigma }_{R_b}$, and the covariance ${\sigma }_{D_{\mathrm{SO}}}^2$ among these variables is

${\sigma }_{D_{\mathrm{SO}}}^2={\left(0.69\left(R_{\mathrm{in}}+R_{\mathrm{int}}\right){\sigma }_{C_b}\right)}^2+{\sigma }_{D_b}^2+{\left(0.69{\sigma }_{R_b}{C}_l\right)}^2+1.38\left(R_{\mathrm{in}}+R_{\mathrm{int}}\right)\mathrm{cov}\left(D_b,C_b\right)$

$+1.38C_l\mathrm{cov}\left(D_b,R_b\right)+0.952C_l\left(R_{\mathrm{in}}+R_{\mathrm{int}}\right)\mathrm{cov}\left(C_b,R_b\right),$ (17.18)

(17.18)

${\sigma }_{D_b}^2={\sigma }_{{D_{\mathrm{SO}}}_0}^2-{\sigma }_{D_{\mathrm{SI}}}^2-1.38\left(R_{\mathrm{in}}+R_{\mathrm{int}}\right)\mathrm{cov}\left(D_b,C_b\right),$ (17.19)

(17.19)

${\sigma }_{C_b}^2=\frac{{\sigma }_{D_{\mathrm{SI}}}}{0.69\left(R_{\mathrm{in}}+R_{\mathrm{int}}\right)}.$ (17.20)

(17.20)

${\sigma }_{R_b}$ is obtained from (17.18) by substituting ${\sigma }_{D_b}$ and ${\sigma }_{C_b}$, respectively, into (17.19) and (17.20).

Consider that ΔC_b, ΔR_b, and ΔD_b are used to obtain the delay variation of each buffer stage Δd_i, which is similar to ΔD_SO. When calculating ${\sigma }_{d_i}$ (similar to recalculating ${\sigma }_{D_{\mathrm{SO}1}}$ through (17.18)), ${\sigma }_{C_b}$, ${\sigma }_{R_b}$, and ${\sigma }_{D_b}$ are again substituted into (17.18). In this procedure, the covariances, cov(D_b, R_b), cov(D_b, C_b) and cov(C_b, R_b), effectively cancel. Consequently, the correlation among ΔC_b, ΔR_b, and ΔD_b does not significantly affect Δd_i as long as Δd_i is based on this same correlation. Since ΔC_b, ΔR_b, and ΔD_b originate from the same source of process variations, these variables are assumed in this model to be fully correlated.

17.2.2 Delay Distribution of Clock Paths

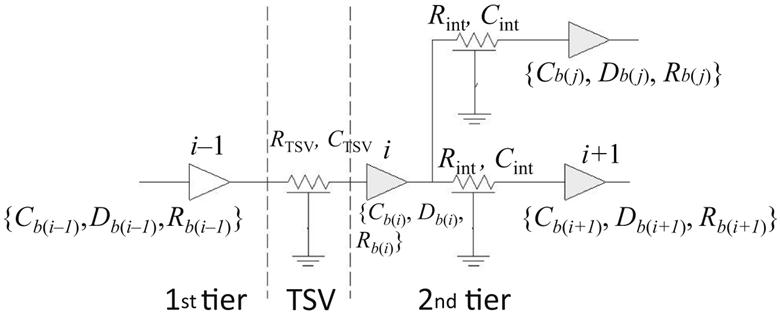
The buffer delay model described in the previous subsection is used to evaluate the delay distribution of clock paths in 3-D circuits. An example of a 3-D clock path is illustrated in Fig. 17.7. The devices in different physical tiers are connected by TSVs [181], which, in turn, are modeled as RC wires of different resistance and capacitance as compared to the horizontal wires (e.g., R_TSV and C_TSV in Fig. 17.7). R_TSV and C_TSV are considered fixed.

Consider the clock path consisting of buffers i−1, i, and i+1. From (17.14) and (17.16), the delay variation Δd_i attributed to the variation of buffer i along a target path is

${\Delta d}_i=0.69\left(R_{\mathrm{in}\left(i\right)}^{\prime }+{\Delta R}_{b\left(i-1\right)}\right){\Delta C}_{b\left(i\right)}+0.69{\Delta R}_{b\left(i\right)}\left(C_{l\left(i\right)}^{\prime }+{\Delta C}_{b\left(i+1\right)}+{\Delta C}_{b\left(j\right)}\right)$

$+0.69R_{b\left(i\right)}^{\prime }{\Delta C}_{b\left(j\right)}+{\Delta D}_{b\left(i\right)},$ (17.21)

(17.21)

$R_{\mathrm{in}\left(i\right)}=R_{b\left(i-1\right)}+R_{\mathrm{TSV}},$ (17.22)

(17.22)

$C_{l\left(i\right)}={2C}_{\mathrm{int}}+C_{b(i+1)}+C_{b(j)},$ (17.23)

(17.23)

where the prime (′) denotes the nominal value. For buffer i, the ΔR_b(i−1) of the upstream buffer and ΔC_b(i+1) of the downstream buffer are both included in (17.21). To determine the delay of a clock path, Δd_i for all of the buffers along this path is summed. In this case, ΔR_b(i−1)ΔC_b(i) and ΔR_b(i)ΔC_b(i+1) are duplicated. One of these two terms therefore needs to be removed. Consequently, Δd_i is rewritten as

${\Delta d}_i=0.69\left(R_{\mathrm{in}\left(i\right)}^{\prime }{\Delta C}_{b\left(i\right)}+{\Delta R}_{b\left(i\right)}(C_{l\left(i\right)}^{\prime }+{\Delta C}_{b\left(i+1\right)}+{\Delta C}_{b\left(j\right)}+R_{b\left(i\right)}^{\prime }{\Delta C}_{b\left(j\right)}\right)+{\Delta D}_{b\left(i\right)}$

$=0.69\left(R_{\mathrm{in}\left(i\right)}^{\prime }{\Delta C}_{b\left(i\right)}+R_{b\left(i\right)}^{\prime }{\Delta C}_{b\left(j\right)}\right)+{\Delta D}_{b\left(i\right)}+{\delta }_i,$ (17.24)

(17.24)

where

${\delta }_i=0.69{\Delta R}_{b\left(i\right)}\left(C_{l\left(i\right)}^{\prime }+{\Delta C}_{b\left(i+1\right)}+{\Delta C}_{b\left(j\right)}\right).$ (17.25)

(17.25)

The variation of ΔC_b is relatively low as compared with the nominal C_b (σ/μ<3% for both D2D and WID variations, as reported in Table 17.1). The observed delay variation of the buffers is also typically much lower than the nominal value (e.g., σ/μ≤5% for both D2D and WID variations, as reported in [638]). δ_i can be approximated using a first order linear Taylor series expansion around zero [637],

${\delta }_i\approx {\left[\frac{\vartheta {\delta }_i}{\vartheta {\Delta R}_{b\left(i\right)}}\right]}_0{\Delta R}_{b\left(i\right)}+{\left[\frac{\vartheta {\delta }_i}{\vartheta {\Delta C}_{b\left(i+1\right)}}\right]}_0{\Delta C}_{b\left(i+1\right)}+{\left[\frac{\vartheta {\delta }_i}{\vartheta {\Delta C}_{b\left(j\right)}}\right]}_0{\Delta C}_{b\left(j\right)}=0.69C_{l\left(i\right)}^{\prime }{\Delta R}_{b\left(i\right)}.$ (17.26)

(17.26)

Table 17.1

Variations in the Electrical Characteristics of the Buffers

Input Slew	Rb (Ω)			Cb (fF)			Db (ps)
	μ	σWID	σD2D	μ	σWID	σD2D	μ	σWID	σD2D
47 (mV/ps)	371	18.8	15.3	4.9	0.04	0.03	19.9	1.04	0.85
	σ/μ	5.1%	4.1%	σ/μ	0.8%	0.7%	σ/μ	5.2%	4.3%
16 (mV/ps)	349	17.8	14.7	5.7	0.31	0.16	24.8	1.49	1.21
	σ/μ	5.1%	4.2%	σ/μ	2.3%	2.1%	σ/μ	6.0%	4.9%
6 (mV/ps)	345	16.7	13.7	7.2	0.08	0.06	30.1	2.19	1.79
	σ/μ	4.8%	4.0%	σ/μ	1.1%	0.9%	σ/μ	7.3%	5.9%

As reported in Table 17.1 and discussed in [632,638] and [639], σ/μ of the transistor characteristics is typically less than 5%. The 3σ variation is smaller than 15% of the nominal R_b and 10% for ΔC_b. Since ΔC_b and ΔR_b are modeled as Gaussian distributions, for more than 99.7% of buffers, ΔC_bΔR_b is lower than 1.5% C_bR_b. Moreover, from the nominal value and standard deviation of C_b, R_b, and D_b, as reported in Table 17.1, 0.69ΔC_bΔR_b and 0.69C_bR_b are, respectively, much lower than ΔD_b and D_b. Consequently, approximating δ_i with (17.26) does not introduce a significant loss of accuracy.

As mentioned previously, ΔR_b(i), ΔC_b(i), and ΔD_b(i) are approximated as Gaussian distributions and can be assumed to be fully correlated. According to (17.24) and (17.26), Δd_i is approximated as a Gaussian distribution.

${\Delta d}_i\mathcal{~}\mathcal{N}\left(0,{\sigma }_{d_i^{\mathrm{D}2\mathrm{D}}}^2+{\sigma }_{d_i^{\mathrm{WID}}}^2\right),$ (17.27)

(17.27)

${\sigma }_{d_i^{\mathrm{D}2\mathrm{D}}}^2=\{\begin{array}{c}{{(\sigma }_1+{\sigma }_2+{\sigma }_3)}^2+{\sigma }_4^2\mathit{if}\mathit{buffers}i\mathit{and}j\mathit{are}\mathit{in}\mathit{different}\mathrm{tiers},\end{array}$ (17.28a)

(17.28a)

${\sigma }_{d_i^{\mathrm{D}2\mathrm{D}}}^2=\{\begin{array}{c}{{(\sigma }_1+{\sigma }_2+{\sigma }_3+{\sigma }_4)}^2\mathit{if}\mathit{buffers}i\mathit{and}j\mathit{are}\mathit{in}\mathit{the}\mathit{same}\mathrm{tier},\end{array}$ (17.28b)

(17.28b)

${\sigma }_{d_i^{\mathrm{WID}}}^2={{(\sigma }_5+{\sigma }_6+{\sigma }_7)}^2+{\sigma }_8^2+2\mathrm{corr}\left(i,j\right){(\sigma }_5+{\sigma }_6+{\sigma }_7){\sigma }_8.$ (17.29)

(17.29)

The terms σ₁ to σ₈ are, respectively,

$\begin{array}{cc}{\sigma }_1=0.69R_{\mathrm{in}\left(i\right)}^{\prime }{\sigma }_{C_{b(i)}^{\mathrm{D}2\mathrm{D}}},& {\sigma }_2=0.69C_{l\left(i\right)}^{\prime }{\sigma }_{R_{b(i)}^{\mathrm{D}2\mathrm{D}}},\\ {\sigma }_5=0.69R_{\mathrm{in}\left(i\right)}^{\prime }{\sigma }_{C_{b(i)}^{\mathrm{WID}}},& {\sigma }_6=0.69C_{l\left(i\right)}^{\prime }{\sigma }_{R_{b(i)}^{\mathrm{WID}}},\end{array}\begin{array}{cc}{\sigma }_3={\sigma }_{D_{b(i)}^{\mathrm{D}2\mathrm{D}}},& {\sigma }_4=0.69R_{b\left(i\right)}^{\prime }{\sigma }_{C_{b(i)}^{\mathrm{D}2\mathrm{D}}},\\ {\sigma }_7={\sigma }_{D_{b(i)}^{\mathrm{WID}}},& {\sigma }_8=0.69R_{b\left(i\right)}^{\prime }{\sigma }_{C_{b(i)}^{\mathrm{WID}}}.\end{array}$

The correlation between buffers i and j is denoted by corr(i, j). A model describing this spatial correlation is discussed in Appendix E.

Consequently, for a 3-D clock path to a sink u that includes n_u clock buffers, the variation of the delay is expressed as the summation of (17.24) of each buffer along the path. The variance of the distribution of a 3-D clock path is a Gaussian distribution consisting of WID and D2D variations of the buffers,

$\Delta D_u=\sum _{i=1}^{n_u}\Delta d_i,$ (17.30)

(17.30)

$\Delta D_u\mathcal{~}\mathcal{N}\left(0,{\sigma }_{D_u^{\mathrm{D}2\mathrm{D}}}^2+{\sigma }_{D_u^{\mathrm{WID}}}^2\right).$ (17.31)

(17.31)

The variation of the delay of a 3-D clock path due to D2D process variations is the sum of the D2D variations of the buffer delay in all of the tiers,

$\Delta D_u^{\mathrm{D}2\mathrm{D}}=\sum _{j=1}^m\Delta D_{u(j)}^{\mathrm{D}2\mathrm{D}},$ (17.32)

(17.32)

$\Delta D_{u(j)}^{\mathrm{D}2\mathrm{D}}=\sum _{j=1}^{n_{u(j)}}\Delta D_{u(j,i)}^{\mathrm{D}2\mathrm{D}},$ (17.33)

(17.33)

where m is the number of tiers spanned by the clock tree. $\Delta D_{u\left(j\right)}^{\mathrm{D}2\mathrm{D}}$ is the variation of the delay of the clock path from the clock source to sink u in tier j. The number of buffers located in tier j along this clock path is denoted by n_u(j). The variation of the delay related to the i^th buffer in tier j is denoted by ${\Delta D}_{u(j,i)}$. Since the D2D variations equally affect the buffers within the same tier, according to (17.27), (17.28), and (17.32), the distribution of $\Delta D_{u\left(j\right)}^{\mathrm{D}2\mathrm{D}}$ is a Gaussian distribution. The D2D variations affect the buffers in different tiers independently and, therefore, $\Delta D_{u\left(j\right)}^{\mathrm{D}2\mathrm{D}}$ is independent of $\Delta D_{u\left(k\right)}^{\mathrm{D}2\mathrm{D}}$ for any j ≠ k. Consequently, according to (17.32), the distribution of $\Delta D_u^{\mathrm{D}2\mathrm{D}}$ is also a Gaussian distribution,

$\Delta D_u^{\mathrm{D}2\mathrm{D}}\mathcal{~}\mathcal{N}\left(0,{\sigma }_{{\mathrm{\Delta }D}_u^{\mathrm{D}2\mathrm{D}}}^2\right),$ (17.34)

(17.34)

${\sigma }_{D_u^{\mathrm{D}2\mathrm{D}}}^2=\sum _{j=1}^m{\sigma }_{D_{u(j)}^{\mathrm{D}2\mathrm{D}}}^2=\sum _{j=1}^m{\left(\sum _{i=1}^{n_{u(j)}}{\sigma }_{D_{u(j,i)}^{\mathrm{D}2\mathrm{D}}}\right)}^2.$ (17.35)

(17.35)

Alternatively, the variation of the delay of a 3-D clock path affected by WID variations is the sum of the WID variations of all of the buffers along this path. Consequently, according to (17.29), the distribution of $\Delta D_u^{\mathrm{WID}}$ is also a Gaussian distribution. The resulting variance of the delay of sink u due to WID variations is

$\Delta D_u^{\mathrm{WID}}\mathcal{~}\mathcal{N}\left(0,{\sigma }_{{\mathrm{\Delta }D}_u^{\mathrm{WID}}}^2\right),$ (17.36)

(17.36)

${\sigma }_{D_u^{\mathrm{WID}}}^2=\sum _{i=1}^{n_u}{\sigma }_{d_i^{\mathrm{WID}}}^2+2\sum _{1\le i<j\le n_u}\mathrm{corr}(i,j){\sigma }_{d_i^{\mathrm{WID}}}{\sigma }_{d_j^{\mathrm{WID}}},$ (17.37)

(17.37)

where corr(i, j) is the correlation between the WID variations of buffers i and j. If buffers i and j are located in different tiers, corr(i, j)=0. The correlation of the impact of WID variations on different buffers within the same tier can be classified as systematic or random. The systematic WID variations typically exhibit a spatial correlation [638,640–642]. For those buffers located within the same tier, two types of correlations for WID variations exist, as described in Appendix E.

17.2.3 Clock Skew Distribution in Three-Dimensional Clock Trees

The clock skew between any pair of sinks in a 3-D clock tree is the difference in the clock delay between these sinks. For a 3-D clock tree with n_sink sinks distributed in m tiers, the nominal and variation of the clock skew s_u,v between sinks u and v are, respectively,

$s_{u,v}^{\prime }=D_u^{\prime }-D_v^{\prime },$ (17.38)

(17.38)

${\Delta s}_{u,v}=\Delta s_{u,v}^{\mathrm{WID}}+\Delta s_{u,v}^{\mathrm{D}2\mathrm{D}}=\Delta D_u^{\mathrm{WID}}-\Delta D_v^{\mathrm{WID}}+\Delta D_u^{\mathrm{D}2\mathrm{D}}-\Delta D_v^{\mathrm{D}2\mathrm{D}}.$ (17.39)

(17.39)

The mean value of Δs_u,v is E(Δs_u,v)=E($\Delta s_{u,v}^{\mathrm{WID}}$)=E($\Delta s_{u,v}^{\mathrm{D}2\mathrm{D}}$)=0. The terms ΔD_u^WID−ΔD_v^WID and ΔD_u^D2D−ΔD_v^D2D are independent. Consequently, $\Delta s_{u,v}^{\mathrm{D}2\mathrm{D}}$ and $\Delta s_{u,v}^{\mathrm{WID}}$ are treated separately. The correlation between every two terms in the expression of $\Delta s_{u,v}^{\mathrm{D}2\mathrm{D}}$ is one or zero (i.e., respectively, fully correlated or uncorrelated). According to (17.32), $\Delta s_{u,v}^{\mathrm{D}2\mathrm{D}}$ is the sum of the terms in different tiers,

$\Delta s_{u,v}^{\mathrm{D}2\mathrm{D}}=\sum _{j=1}^m{\Delta s}_{{(u,v)}_j}^{\mathrm{D}2\mathrm{D}},\Delta s_{{(u,v)}_j}^{\mathrm{D}2\mathrm{D}}=\sum _{i=1}^{n_{u(j)}}{\Delta D}_{u(j,i)}^{\mathrm{D}2\mathrm{D}}-\sum _{i=1}^{n_{v\left(j\right)}}{\Delta D}_{v\left(j,i\right)}^{\mathrm{D}2\mathrm{D}},$ (17.40)

(17.40)

where ${\Delta D}_{u(j,i)}^{\mathrm{D}2\mathrm{D}}$ is the D2D delay variation related to the i^th buffer in the j^th tier along the clock path ending at sink u. The number of buffers in the j^th tier along this path is denoted as n_u(j).

All of the buffers in the same tier are equally affected by D2D variations, meaning that the correlation between each pair of variables in (17.40) is one. Since ${\Delta D}_{u(j,i)}^{\mathrm{D}2\mathrm{D}}$ and ${\Delta D}_{v(j,i)}^{\mathrm{D}2\mathrm{D}}$ are both modeled as a Gaussian distribution, ${\Delta D}_{s{(u,v)}_j}^{\mathrm{D}2\mathrm{D}}$ is also a Gaussian distribution. In (17.40), ∀ j₁ ≠ j₂ (1≤j₁, j₂≤m) ${\Delta D}_{s{(u,v)}_{j_1}}^{\mathrm{D}2\mathrm{D}}$ is independent of ${\Delta D}_{s{(u,v)}_{j_2}}^{\mathrm{D}2\mathrm{D}}$. Consequently, $\Delta s_{u,v}^{\mathrm{D}2\mathrm{D}}$ is also described by a Gaussian distribution,

$\Delta s_{u,v}^{\mathrm{D}2\mathrm{D}}\mathcal{~}\mathcal{N}\left(0,{\sigma }_{s_{u,v}^{\mathrm{D}2\mathrm{D}}}^2\right),$ (17.41)

(17.41)

${\sigma }_{D_u^{\mathrm{D}2\mathrm{D}}}^2=\sum _{j=1}^m{\sigma }_{s_{u,v(j)}^{\mathrm{D}2\mathrm{D}}}^2=\sum _{j=1}^m{\left(\sum _{i=1}^{n_{u(j)}}{\sigma }_{D_{u\left(j,i\right)}^{\mathrm{D}2\mathrm{D}}}-\sum _{i=1}^{n_{v(j)}}{\sigma }_{D_{v\left(j,i\right)}^{\mathrm{D}2\mathrm{D}}}\right)}^2.$ (17.42)

(17.42)

According to (17.37), the distribution of $\Delta s_{u,v}^{\mathrm{WID}}$ is also a Gaussian distribution,

$\Delta s_{u,v}^{\mathrm{WID}}\mathcal{~}\mathcal{N}\left(0,{\sigma }_{s_{u,v}^{\mathrm{WID}}}^2\right),$ (17.43)

(17.43)

${\sigma }_{s_{u,v}^{\mathrm{WID}}}^2=\sum _{i=n_{u,v}+1}^{n_u}{\sigma }_{D_{u\left(i\right)}^{\mathrm{WID}}}^2+\sum _{j=n_{u,v}+1}^{n_v}{\sigma }_{D_{v\left(j\right)}^{\mathrm{WID}}}^2+2\sum _{\begin{array}{c}i,j=n_{u,v}+1\\ i<j\end{array}}^{n_u}\mathrm{corr}\left(i,j\right){\sigma }_{D_{u\left(i\right)}^{\mathrm{WID}}}{\sigma }_{D_{u\left(j\right)}^{\mathrm{WID}}}$

$+2\sum _{\begin{array}{c}i,j=n_{u,v}+1\\ i<j\end{array}}^{n_v}\mathrm{corr}\left(i,j\right){\sigma }_{D_{v\left(i\right)}^{\mathrm{WID}}}{\sigma }_{D_{v\left(j\right)}^{\mathrm{WID}}}-2\sum _{\begin{array}{c}{n}_{u,v}+1\le i\le n_u\\ n_{u,v}+1\le j\le n_v\end{array}}\mathrm{corr}\left(i,j\right){\sigma }_{D_{u\left(i\right)}^{\mathrm{WID}}}{\sigma }_{D_{v\left(j\right)}^{\mathrm{WID}}},$ (17.44)

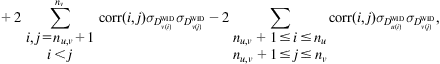(17.44)

where n_u,v is the number of buffers shared by the clock paths ending at sinks u and v, as depicted in Fig. 17.8. Downstream the buffers n_u,v, the subpaths to u and v do not share a buffer.

According to (17.39) through (17.44), the variation of the clock skew Δs_u,v between sinks u and v in a 3-D clock tree is modeled as a Gaussian distribution,

$\Delta s_{u,v}\mathcal{~}\mathcal{N}\left(0,{\sigma }_{s_{u,v}^{\mathrm{WID}}}^2+{\sigma }_{s_{u,v}^{\mathrm{D}2\mathrm{D}}}^2\right).$ (17.45)

(17.45)

If the maximum tolerant skew variation is ΔS≥0, the probability that a 3-D clock tree satisfies this constraint is

$P\left(\left|s_{u,v}\right|\le \Delta S\right)={\int }_{-\Delta S-s_{u,v}^{\prime }}^{\Delta S-s_{u,v}^{\prime }}{f}_{\Delta s_{u,v}}\left(t\right)\mathit{dt},$ (17.46)

(17.46)

$f_{\Delta s_{u,v}}\left(t\right)=\frac{1}{\sqrt{2\pi {\sigma }_{s_{u,v}}^2}}{e}^{-t^2/(2{\sigma }_{s_{u,v}}^2)}.$ (17.47)