6
![]()
On Examinee Choice
in Educational Testing
If you allow choice, you will regret it; if you don't
allow choice, you will regret it; whether you allow
choice or not, you will regret both.
—Soren Kierkegaard 1986, 24
In chapters 2 and 5 we explored the difficulties encountered in making comparisons among candidates when the candidates themselves are the ones who decide which aspects of their experience and ability to present. The difficulties in making such comparisons fairly can be overwhelming. Let us now consider the more limited situation that manifests itself when the examination scores of students who are to be compared are obtained from test items that the students have chosen themselves. Such a situation occurred often in the beginning of the twentieth century, but gradually fell out of favor as evidence accumulated that highlighted the shortcomings of such “build it yourself” exams. But the lessons learned seem to have been forgotten, and there is renewed hope that examinee choice can improve measurement, particularly when assessing what are called generative or constructive processes in learning. To be able to measure such processes, directors of testing programs believe they must incorporate items that require examinees to respond freely (what, in testing jargon, are called “constructed response” items) into their previously highly constrained (multiple choice) standardized exams.
It is hoped that items that require lengthy responses, such as essays, mathematical proofs, experiments, portfolios of work, or other performance-based tasks are better measures of deep understanding, broad analysis, and higher levels of performance than responses to traditional multiple-choice items. Examples of tests currently using constructed response items are the College Board's Advanced Placement examinations in United States History, European History, United States Government and Politics, Physics, Calculus, and Chemistry. There are many others.
Multiple-choice items are small and take only a modest amount of time to answer. Thus a one-hour exam can easily contain forty to fifty such items. Each item contributes only a small amount to the examinee's final score. This has two important benefits. First, it allows the test developer to provide a reasonable representation of the content of the area being examined. And second, examinees are not affected too severely if a question or two represent material that was not covered by their particular course.
But when an exam consists, in whole or in part, of constructed response items, this is no longer true. Constructed response items like essays take a much longer time to answer, and so the test developer must face unfortunate options:
1. Use only a small number of such items, thus limiting the coverage of the domain of the test.
2. Increase the length of time it takes to administer the exam; this is usually impractical.
3. Confine the test questions to a core curriculum that all valid courses ought to cover. This option may discourage teachers from broadening their courses beyond that core.
To try to resolve this difficult situation it is common practice to provide a pool of questions and to allow each examinee to choose a subset of them to answer.
But what are we estimating when we allow choice? When a test is given, we ordinarily estimate a score that represents the examinee's proficiency. The usual estimate of proficiency is based on estimated performance from a sample drawn from the entire distribution of possible items. Most practitioners I have spoken to who favor allowing choice, argue that choice provides the opportunity for the examinees to show themselves to best advantage. However, this is only true if examinees choose the item that would give them the highest score.
Unfortunately, choice items are typically not of equal difficulty, despite the best efforts of test builders to make them so. This fact, combined with the common practice of not adjusting the credit given to mirror the differences in item difficulty, yields the inescapable conclusion that it matters what choice an examinee makes. Examinees who chose the more difficult question will, on average, get lower scores than if they had chosen the easier item. The observation that all examinees do not choose those items that will show their proficiency to best advantage completes this unhappy syllogism.
Even in the absence of attractive alternatives, is allowing examinee choice a sensible strategy? Under what conditions can we allow choice without compromising the fairness and quality of the test? I will not provide a complete answer to these questions. I will, however, illustrate some of the pitfalls associated with allowing examinee choice; provide a vocabulary and framework that aids in the clear discussion of the topic; outline some experimental steps that can tell us whether choice can be implemented fairly; and provide some experimental evidence that illuminates the topic.
Let us begin with a brief history of examinee choice in testing, in the belief that it is easier to learn from the experiences of our clever predecessors than to try to relive those experiences.
A SELECTIVE HISTORY OF CHOICE IN EXAMS
I shall confine my attention to some college entrance exams used during the first half of the twentieth century in the United States. The College Entrance Examination Board (CEEB) began testing prospective college students at the juncture of the nineteen and twentieth centuries. By 1905 exams were offered in thirteen subjects: English, French, German, Greek, Latin, Spanish, Mathematics, Botany, Chemistry, Physics, Drawing, Geography, and History.1 Most of these exams contained some degree of choice. In addition, all of the science exams used portfolio assessment, as it might be called in modern terminology. For example, on the 1905 Botany exam 37 percent of the score was based on the examinee's laboratory notebook. The remaining 63 percent was based on a ten-item exam. Examinees were asked to answer seven of those ten items, which yielded the possibility of 120 different unique examinee-created “forms.”
The computation of the number of choice-created forms is further complicated by some remarkably vague exam questions.2 Question 10 from the 1905 Botany exam illustrates this profound lack of specificity:3
10. Select some botanical topic not included in the questions above, and write a brief exposition of it.
The Chemistry and Physics exams shared the structure of the Botany exam.
As the CEEB grew more experienced, the structure of its tests changed. The portfolio aspect disappeared by 1913, when the requirement of a teacher's certification that the student had, in fact, completed a lab course was substituted for the student's notebook. By 1921 this certification was no longer required.
The extent to which examinees were permitted choice varied; see Table 6.1, in which the number of possible examinee-created “forms” is listed for four subjects over thirty-five years. The contrast between the flamboyance of the English exam and the staid German exam is instructive. Only once, in 1925, was any choice allowed on the German exam (“Answer only one of the following six questions”). The lack of choice seen in the German exam is representative of all of the foreign language exams except Latin. The amount of choice seen in Physics and Chemistry parallel that for most exams that allowed choice. The English exam between 1913 and 1925 is unique in terms of the possible variation.4 No equating of these examinee-constructed forms for possible differential difficulty was considered.
TABLE 6.1
Number of Possible Test Forms Generated
by Examinee choice Patterns

By 1941 the CEEB offered fourteen exams, but only three (American History, Contemporary Civilization, and Latin) allowed examinee choice. Even among these, choice was sharply limited:
• In the American History exam there were six essay questions. Essays 1, 2, and 6 were mandatory. There were three questions about the American Constitution (labeled 3A, 4A, and 5A) as well as three parallel questions about the British constitution (3B, 4B and 5B). The examinee could choose either the A questions or the B questions.
• In the Contemporary Civilization exam there were six essay questions. Questions 1-4 and 6 were all mandatory. Question 5 consisted of six short-answer items out of which the examinee had to answer five.
• The Latin exam had many parts. In sections requiring translation from Latin to English or vice versa, the examinee often had the opportunity to pick one passage from a pair to translate.
In 1942, the last year of the program, there were fewer exams given; none allowed examinee choice. Why did the use of choice disappear over the forty years of this pioneering examination program? My investigations did not yield a definitive answer, although many hints suggest that issues of fairness propelled the CEEB toward the test structure on which it eventually settled. My insight into this history was sharpened during the reading of Carl Brigham's remarkable 1934 report on “the first major attack on the problem of grading the written examination.”5 This exam required the writing of four essays. There were six topics; 1 and 6 were required of all examinees and there was a choice offered between topics 2 and 3 and between topics 4 and 5. The practice of allowing examinee choice was termed “alternative questions.”
As Brigham noted,
When alternative questions are used, different examinations are in fact set for the various groups electing the different patterns. The total score reported to the college is to a certain extent a sum of the separate elements, and the manner in which the elements combine depends on their intercorrelation. This subject is too complex to be investigated with this material.
Brigham's judgment of the difficulty is mirrored by Princeton psychometrician Harold Gulliksen, who, in his classic 1950 text wrote, “In general it is impossible to determine the appropriate adjustment without an inordinate amount of effort. Alternative questions should always be avoided.”
Both of these comments suggest that while adjusting for the effects of examinee choice is possible, it is too difficult to do within an operational context. I suspect that even these careful researchers underestimated the difficulty of satisfactorily accomplishing such an adjustment.6 This view was supported by legendary psychometrician Ledyard Tucker (1910-2004),7 who said, “I don't think that they knew how to deal with choice then. I'm not sure we know how now.”
The core of the problem of choice is that when it is allowed, the examinees' choices generate what can be thought of as different forms of the test. These forms may not be of equal difficulty. When different forms are administered, standards of good testing practice require that those forms be statistically equated so that individuals who took different forms can be compared fairly. Perhaps, through pretesting and careful test construction, it may be possible to make the differences in form difficulty sufficiently small that further equating is not required. An unbiased estimate of the difficulty of any item can not be obtained from a self-selected sample of the examinee population. The CEEB made no attempt to avoid such a sample. Perhaps that is why Brigham said, “This subject is too complex to be investigated with this material.”
ARE CHOICE ITEMS OF EQUAL DIFFICULTY?
When choice items are prepared, item writers strive to make them of equal difficulty. But this is a task that seems to be beyond current test construction methods. Until recently, evidence about the relative difficulty of such items was suggestive, but equivocal. Let me illustrate this point with three simple examples. The first and the second come from operational testing programs and the third from a special data-gathering effort.
Example 1:1968 AP Chemistry Test
Shown in table 6.2 are results8 for a form of the College Board's Advanced Placement chemistry test. One group of examinees chose to take problem 4 and a second group chose problem 5. While their scores on the common multiple-choice section were about the same (11.7 vs. 11.2 out of a possible 25), their scores on the choice problem were very different (8.2 vs. 2.7 on a ten-point scale). There are several possible conclusions to be drawn from this. Four among them are the following:
1. Problem 5 is a good deal more difficult than problem 4.
2. Small differences in performance on the multiple-choice section translate into much larger differences on the free response questions.
TABLE 6.2
Average scores on AP chemistry 1968

3. The proficiency required to do the two problems is not strongly related to that required to do well on the multiple-choice section.
4. Item 5 is selected by those who are less likely to do well on it.
Investigation of the content of the questions as well as studies of the dimensionality of the entire test suggest that conclusion (1) is the most credible. This interpretation would suggest that scores on these two examinee-created test forms ought to have been equated. They were not.
Example 2: 1988 AP United States History Test
The first example indicated that those who chose the more difficult problem were placed at a disadvantage. In this example I identify more specifically the examinees who tended to choose more difficult items. Consider the results shown in Figure 6.1 from the 1988 administration of the College Board's Advanced Placement test in United States history. This test comprises 100 multiple-choice items and two essays. Essay 1 is mandatory; the second is chosen by the examinee from among five topics (2-6). Shown in Figure 6.1 are the average scores given for each of those topics, as well as the proportion of men and women who chose it.
Topic 3 had the lowest average scores for both men and women. The usual interpretation of this finding is that topic 3 was the most difficult. This topic was about twice as popular among women as among men. An alternative interpretation of these findings might be that the lowest proficiency examinees chose this topic, and that a greater proportion of women than men fell into this category. This illustrates again how any finding within a self-selected sample yields ambiguous interpretations.
Similar studies with similar findings have been carried out on all of the AP tests that allow choice.9 There are also substantial sex and ethnic differences in choice on third-, fifth-, and eighth-grade passage-based reading comprehension tests.10 The phenomenon of students choosing poorly is so widespread that evidence of it occurs wherever one looks. In one description of the effect of choice on a test of basic writing, the investigators found that the more that examinees liked a particular topic, the lower they scored on an essay they subsequently wrote on that topic!11

Figure 6.1. Scores on the choice essays for the 1988 AP United States History test for men and women examinees
Although test developers try to make up choice questions that are of equivalent difficulty, they are rarely successful. Of course this conclusion is clouded by possible alternative explanations that have their origin in self-selection: for example, the choice items are not unequally difficult, but rather the people who choose them are unequally proficient. So long as there is self-selection, this alternative cannot be completely dismissed, although it can be discredited through the use of additional information. If it can be shown that choice items are not of equal difficulty, it follows that some individuals will be placed at a disadvantage by their choice of item—they choose to take a test some of whose items are more difficult than those on a corresponding test for other examinees—at least to the extent that this extra difficulty is not adjusted away in the scoring.
Example 3: The Only Unambiguous Data on Choice and Difficulty
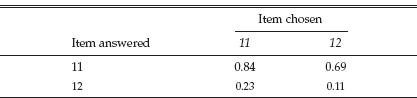
In a special data-gathering effort, we repeatedly presented examinees with a choice between two items, but then required them to answer both.12 One aspect of the results appears in Table 6.3. The column labeled “Item difficulty” contains the percentage of students nationally who answered that item correctly.13 We see that even though item 12 was much more difficult than item 11, there were still some students who chose it.
Perhaps the examinees who chose item 12 did so because they had some special knowledge that made this item less difficult for them than item 11. Table 6.4 shows the performance of examinees on each of these items broken down by the items they chose. Note that 11 percent of those examinees who chose item 12 responded correctly, whereas 69 percent of them answered item 11 correctly. Moreover, this group performed more poorly on both of the items than examinees who chose item 11. The obvious implication drawn from this example is that examinees do not always choose wisely, and that less proficient examinees exacerbate matters through their unfortunate choices. Data from the rest of this experiment consistently supported these conclusions.
The conclusion drawn from many results like this is that as examinees' ability increases they tend to choose more wisely—they know enough to be able to determine which choices are likely to be the least difficult. The other side of this is as ability declines choice becomes closer and closer to random. What this means is that, on average, lower-ability students, when given choice, are more likely to choose more difficult items than their competitors at the higher end of the proficiency scale. Thus allowing choice will tend to exacerbate group differences.
TABLE 6.3
The Difficulty and Popularity of Two choice Items

TABLE 6.4
The Proportion of Students Getting Each Item correct Based
on Item Selected
STRATEGIES FOR FAIR TESTING
WHEN CHOICE IS ALLOWED
I will now examine two alternative strategies for achieving the primary goal of examinee choice: to provide the opportunity for examinees to show themselves to the best advantage. The first is to aid students in making wiser choices; the second is to diminish the unintended consequences of a poor choice through statistical equating of the choice items.
What Are the Alternative Strategies?
There appear to be two paths that can be followed: eliciting wiser choices by examinees or equating test forms. The second option removes the necessity for the first; in fact it makes examinee choice unnecessary.
How can we improve examinees' judgment about which items to select? I fear that this can be done optimally only by asking examinees to answer all items, and then scoring just those responses that yield the highest estimate of performance. This strategy is not without its drawbacks. First, it takes more testing time, and choice is often instituted to keep testing time within practical limits. Second, many examinees, upon hearing that “only one of the six items will be counted” will only answer one. Thus, this strategy may commingle measures of grit, choice-wisdom, and risk aversion with those of proficiency. It also adds in a positive bias associated with luck.
A more practical approach might be to try to improve the instructions to the examinees about how the test is to be graded, so as to help them make better choices. Perhaps it would help if the instructions about choice made it clear that there is no advantage to answering a hard item correctly relative to answering an easy one, if such is indeed the case. Current instructions do not address this issue. For example, the instructions about choice on the 1989 AP Chemistry test, reproduced in their entirety are,
Solve ONE of the two problems in this part. (A second problem will not be scored).
Contrast this with the care that is taken to instruct examinees about the hazards of guessing. These are taken from the same test:
Many candidates wonder whether or not to guess the answers to questions about which they are not certain. In this section of the examination, as a correction for haphazard guessing, one-fourth of the number of questions you answer incorrectly will be subtracted from the number you answer correctly. It is improbable, therefore, that mere guessing will improve your score significantly; it may even lower your score, and it does take time. If however, you are not sure of the correct answer but have some knowledge of the question and are able to eliminate one or more of the answer choices as wrong, your chance of getting the right answer is improved, and it may be to your advantage to answer such a question.
Perhaps with better instructions the quality of examinee choices can be improved. At the moment there is no evidence supporting the conjecture that they can be, or if so, by how much. An experimental test of the value of improved instructions could involve one randomly selected group with the traditional instructions and another with a more informative set. We could then see which group has higher average scores on the choice section.
I am not confident that this option solves the problem of making exams that allow choice fairer. To do so requires reducing the impact of unwise choice. This could be accomplished by adjusting the scores on the choice items statistically for their differential difficulty: the process called equating that we have already discussed.
How Does Equating Affect the Examinee's Task?
Equating appears, at first blush, to make the examinee's task of choosing more difficult still. If no equating is done the instructions to the examinee should be
Answer that item which seems easiest to you.
We hope that the examinees choose correctly, but we will not know if they do not. If we equate the choice items (give more credit for harder items than easier ones), the instructions should be
Pick that item which, after we adjust, will give you the highest score.
This task could be akin to the problem faced by competitive divers, who choose their routine of dives from within various homogeneous groups of dives. The diver's decision is informed by several factors:
• Knowledge of the “degree of difficulty” of each dive
• Knowledge of the concatenation rule by which the dive's difficulty and the diver's performance rating are combined (they are multiplied)
• Knowledge, obtained through long practice, of what his or her score is likely to be on all of the dives
Armed with this knowledge, the diver can select a set of dives that is most likely to maximize his or her total score.
The diver's scenario is one in which an individual's informed choice provides a total score that seems to be close enough to optimal for useful purposes. Is a similar scenario possible within the plausible confines of standardized testing? Let us examine the aspects of required knowledge point by point.
Specifying how much each item will count in advance is possible, either by calculating the empirical characteristics of each item from pretest data or, as is currently the case, by specifying how much each one counts by fiat. I favor the former, because it allows each item to contribute to total score in a way that minimizes measurement error. An improvident choice of a priori weights can have a serious deleterious effect on measurement accuracy.14
Specifying the concatenation rule (how examinee performance and item characteristics interact to contribute to the examinee's score) in advance is also possible, but may be quite complex. Perhaps a rough approximation can be worked out, or perhaps one could present a graphical solution, but for now this remains a question. The difficulties that we might have with specifying the concatenation rule are largely technical, and workable solutions could probably be developed.
A much more formidable obstacle is providing the examinees with enough information so that they can make wise choices. This seems completely out of reach, for even if examinees know how much a particular item will, if answered correctly, contribute to their final score, it does no good unless the examinees have a good idea of their likelihood of answering the item correctly. The extent to which such knowledge is imperfect would then correspond to the difference between the score that is obtained and the optimal score that could have been obtained with a perfect choice. The nature of security associated with modern large-scale testing makes impossible the sort of rehearsal that provides divers with accurate estimates of their performance under various choice options.
The prospect appears bleak for simultaneously allowing choice and satisfying the canons of good practice that require the equating of test forms of unequal difficulty. The task that examinees face in choosing items when they are adjusted seems too difficult. But is it? There remain two glimmers of hope:
1. Equating the choice items before scoring them
2. Declaring that the choice is part of the item, and so if you choose unwisely, tough
Option 1, the equating of the various choice forms, seems better. If we can do this, the examinees should be indifferent about which items they answer, because successful equating means that an examinee will receive, in expectation, the same score regardless of the form administered. This is happy, but ironic, news; for it appears that we can allow choice and have fair tests only when choice is unnecessary. To answer the question posed at the beginning of this section: When we do not equate selected items, the problem of choice faced by the examinee can be both difficult and important. When we do equate the items, the selection problem simultaneously becomes much more difficult but considerably less important.
Equating choice items involves arranging each item to be answered by a randomly selected subset of the population. For example, if we had a section with three items and we wanted examinees to choose two of them to answer, we would need to assign one randomly selected third of the examinees to answer item 1 and allow them to choose between items 2 and 3. A second group would be assigned item 2 and be allowed to choose between 1 and 3; and the last group would have to answer item 3 and get to choose between 1 and 2. In this way we can obtain unbiased estimates of the difficulties of all three items and the examinees would still have some choice. I will not go further into the more technical details of how to equate choice items, as that discussion is beyond the scope of this chapter.
Option 2, making the choice part of the item, is an interesting possibility and I will devote all of chapter 7 to its exploration.
What Can We Learn from Choice Behavior?
Thus far, my proposed requirements prior to implementing examinee choice fairly require a good deal of work on the part of both the examinee and the examiner. I am aware that extra work and expense are not part of the plan for many choice tests. Often choice is allowed because there are too many plausible items to be asked and too little time to answer them. Is all of this work really necessary? Almost surely. At a minimum one cannot know whether it is necessary unless it is done. To paraphrase Derek Bok's comment on the cost of education, if you think doing it right is expensive, try doing it wrong. Yet many well-meaning and otherwise clear-thinking individuals ardently support choice in exams. Why? The answer to this question must, perforce, be impressionistic. I have heard a variety of reasons. Some are nonscientific; one, from educational researcher Karen Scheingold was “To show the examinees that we care.” The implication is that by allowing choice we are giving examinees the opportunity to do their best. I find this justification difficult to accept, because there is overwhelming evidence to indicate that this goal is unlikely to be accomplished. Which is more important, fairness, or the appearance of fairness? Ordinarily the two go together, but when they do not, we must be fair, and do our best to explain why.
DISCUSSION
So far I have painted a bleak psychometric picture for the use of examinee choice within fair tests. To make tests with choice fair requires equating the test forms generated by the choice for their differential difficulty. Accomplishing this requires either some special data-gathering effort or trust in assumptions about the unobserved responses that, if true, obviate the need for choice. If we can successfully equate choice items, we have thus removed the value of choice in any but the most superficial sense.
Thus far I have confined the discussion to situations in which it is reasonable to assign any of the choice items to any examinee. Such an assumption underlies the notions of equating. I will call situations in which examinees are given such a choice small choice.
Small Choice
Small choice is used most commonly because test designers believe that measurement of the underlying construct may be contaminated by the particular context in which the material is embedded. It is sometimes thought that a purer estimate of the underlying construct may be obtained by allowing examinee choice from among several different contexts. Consider, for example the following two versions of the same math problem:
1. The distance between the Earth and the Sun is 93 million miles. If a rocket ship took 40 days to make the trip, what was its average speed?
2. The Kentucky Derby is one and one-fourth miles in length. When Northern Dancer won the race with a time of 2 minutes, what was his average speed?
The answer to both problems may be expressed in miles per hour. Both problems are formally identical, except for differences in the difficulty of the arithmetic. Allowing an examinee to choose between these items might allow us to test the construct of interest (Does the student know the relation Rate × Time = Distance?), while at the same time letting the examinees pick the context within which they feel more comfortable.
The evidence available so far tells us that with enough preparatory work small choice can be implemented on exams fairly. But if this option is followed carefully the reasons for allowing choice have been mooted.
But What about Big Choice?
It was late at night in a dimly lit chamber hidden in the bowels of the admissions office of Ivy University. Through bleary eyes, Samantha Stewart, the admissions director, was reviewing the pile of dossiers that represented the entering class of 2014. Almost all of the tough decisions had been made. But one remained that she alone must deal with. There was but a single opening with two worthy competitors for that very lact spot. Both applicants had taken a rigorous program of study in high school and both excelled. Their SAT scores were nearly identical and their letters of recommendation could not have been better. One student was first violin in the all-state orchestra and the other was first-string quarterback on the all-state football team. Either would make a fine addition to the class, but there was only room for one. How was the director to decide? She was faced with trying to answer a seemingly impossible question: Was student A a better violinist than student B was a quarterback?
So far we have focused on small choice, in which we could plausibly ask individuals to answer any of the options available. We concluded that small choice is possible to do fairly, but only with a substantial amount of preparation. What about big choice, illustrated in the previous example? This is a much more difficult problem. Can we find an evidence-based solution?
Throughout the educational process decisions are made using nonrandomly selected data. Admissions to college are decided among individuals whose dossiers contain mixtures of material; one high school student may opt to emphasize courses in math and science, whereas another may have taken advanced courses in French and Spanish. One student might have been editor of the school newspaper, another captain of the football team, and yet a third might have been first violin in the orchestra. All represent commitment and success; how are they to be compared? Is your French better than my calculus? Is such a comparison sensible? Admissions offices at competitive universities face these problems all the time; dismissing them is being blind to reality. Moreover there is obvious sense in statements like “I know more physics than you know French.” Or “I am a better runner than you are a swimmer.” Cross-modal comparisons are not impossible, given that we have some implicit underlying notion of quality. How accurate are such comparisons? Can we make them at all when the differences between the individuals are subtle? How do we take into account the difficulty of the accomplishment? Is being an all-state athlete as distinguished an accomplishment as being a Merit Scholarship finalist?
How can we understand comparisons like these? Can we adapt the solutions for small choice to work much further out on the inference limb?
Big Choice
In contrast to small choice, big choice is a situation in which it makes no sense to insist that all individuals attempt all tasks (e.g., it is of no interest or value to ask the editor of the school yearbook to quarterback the football team for a series of plays in order to gauge proficiency in that context). Making comparisons among individuals after they have made a big choice is quite common. College admissions officers compare students who have chosen to take the French achievement test against those who opted for one in physics, even though their scores are on completely different scales. Companies that reward employees with merit raises usually have a limited pool of money available for raises and, in the quest for an equitable distribution of that pool, must confront such imponderable questions as “Is person A a more worthy carpenter than person B is a salesman?” At the beginning of this chapter I postponed big choice while attempting to deal with the easier problems associated with small choice.
Most of what we have discussed so far leans heavily on sampling responses to choice items from those who hadn't selected them and thus applies primarily to the small-choice situation. Can we make useful comparisons in the context of big choice? Yes, but it depends on the goal of the test. There are many possible goals of a testing program. For now I will consider only three: contest, measurement, and goad to induce change.
When a test is a contest, we are using it to determine a winner. We might wish to choose a subset of examinees for admission, for an award, or for a promotion. In a contest we are principally concerned with fairness. All competitors must be judged under the same rules and conditions. We are not concerned with accuracy, except to require that the test be sufficiently accurate to tell us the order of finish unambiguously.
When a test is used for measurement, we wish to make the most accurate possible determination of some characteristic of an examinee. Usually measurement has associated with it some action; we measure blood pressure and then consider exercise and diet; we measure a child's reading proficiency and then choose suitable books; we measure mathematical proficiency and then choose the next step of instruction. Similarly we employ measurement to determine the efficacy of various interventions. How much did the diet lower blood pressure? How much better was one reading program than another? When measuring we are primarily concerned with accuracy. Anything that reduces error may fairly be included on the test.
When a test is a goad to induce change, we are using the test to influence behavior. Sometimes the test is used as a carrot or a stick to influence the behavior of students; we give the test to get students to study more assiduously. Sometimes the test is used to modify the behavior of teachers; we construct the test to influence teachers' choice of material to be covered. This goal has been characterized as measurement-driven instruction,15 which has engendered rich and contentious discussions. I will not add to them here.16 At first blush it might appear that when a test is being used in this way, issues of fairness and measurement precision are not important, although the appearance of fairness may be. However, that is false. When a test is used to induce change, the obvious next question must be, “How well did it work?” If we used the test to get students to study more assiduously, or to study specific material, how much did they do so? How much more have the students learned than they would have under some other condition? The other condition might be “no announced test” or it might be with a test of a different format. There are obvious experimental designs that would allow us to investigate such questions—but all require measurement.17 Thus, even when the purpose of the test is to influence behavior, that test still ought to satisfy the canons of good measurement practice.
Making useful comparisons in the context of big choice is only possible for tests as contests, at least for the moment. When there is big choice, we can set out rules that will make the contest fair. We are not able to make the inferences that are usually desirable for measurement. Let us begin by considering an instructive (and relatively simple) example, the Ironman Triathlon.
Let us think of the Ironman Triathlon as a three-item test:
1. Swim 2.5 miles. This item takes a great swimmer forty-five minutes.
2. Cycle 125 miles. This item takes a great cyclist more than four hours.
3. Run 26.2 miles. This item takes a great runner more than two hours.
Score equals total time. As a contest, it is fair, for everybody knows the scoring rules before they begin.
Suppose we allow choice (pick two of three). Anyone who chooses item 2 is a fool (or doesn't know how to swim).
If we don't tell anyone about the expected amount of time, is the contest with choice still fair? Suppose we assign items to individuals? What would we need to do now to make the test fair?
Possible solution: We could make the items equally difficult. An approximation to such a manipulation is this:
1. Swim 7.5 miles. This item takes a great swimmer more than two hours.
2. Cycle 60 miles. This item takes a great cyclist more than two hours.
3. Run 26.2 miles. This item takes a great runner more than two hours.
Obviously, allowing choice on this modified version (an equilateral triathlon?) is more reasonable than the original formulation, but a lot more work would need to be done to assure that these events are more nearly of equal difficulty than merely using the times of world record holders.
The triathlon is a comparatively new sporting event. The relative dimensions of its component parts may not be what they will eventually become as issues of fairness and competitiveness get worked through with additional data. Thus it is illuminating to examine a more mature event of similar structure; the Olympic decathlon. But before we get to the decathlon let us take a brief theoretical aside to discuss some of the basics of measurement, and what is required to be able to define a winner in an event like the decathlon.
An Aside on Measurement Scales
When we measure anything, the quality of the measurement depends on the instrument we use. More precise measurement requires better tools. We must first decide how much precision is needed for the purpose at hand before we can pick the measuring instrument.
Measurement tools form a continuum that range from primitive to advanced. Let me select four levels of measurement from this range.
At the primitive end we might merely name things: table, chair, horse, dog. Measuring an object means putting it into a category. This sort of measurement is called, for obvious reasons, a nominal scale. Such a measurement is not much help for scoring a decathlon, for there is no ordering among the categories. A chair is neither more nor less than a pizza. The sole requirement for a measurement to be considered nominal is that the classification criteria must be unambiguous; an object cannot simultaneously be both a pizza and a chair.
Our next step up the scale is measurement that allows ordering. As such it is called an ordinal scale. To be considered ordinal the measure must satisfy the criterion for nominal measurement plus two additional criteria:
1. Connectedness: Either a ≥ b or b ≥ a.
2. Transitivity: If a ≥ b and b ≥ c, then a ≥ c.
These two criteria seem simple, but a moment's thought reveals how such characteristics separate nominal scale measurement from ordinal. A table is not more than or less than a pizza, hence neither of these two criteria make sense. But if we are to measure some contest we must have a metric in place that allows us to say that either performance a is better than or equal to performance b, or it is worse. Transitivity is also important and its implications are subtle. We will discuss it at greater length shortly. An example of an ordinal scale is Mohs' scale of hardness of minerals, in which any mineral is defined to be harder than another if it can scratch it, and lower if it is scratched. Thus a diamond is very high on the scale, for it will scratch most other things, and talc is very low, for most things will scratch it. Note that this scale satisfies the two requirements. It is easy to see why we must have at least an ordinal scale in order to decide any contest.
Next we come to interval scales. Such measurement has to satisfy the requirements of an ordinal scale as well as the additional characteristic that the difference between measurements must be meaningful and have the same meaning throughout the scale. An example is the Celsius scale of temperature. It clearly satisfies the ordinal requirements, but in addition the 10-degree difference between, say, 70 degrees and 60 degrees has the same meaning (in some physical sense) as a 10-degree difference anywhere else on the scale. Interval scale properties are critical for contests whose scores add together pieces from various parts.
Note that ratio inferences, for example, “80 degrees is twice as warm as 40 degrees,” make no sense when we have just an interval scale. In order for such inferences to be sensible we need a rational zero. Thus ratio statements of temperature make sense on the Kelvin scale, but not Celsius. This brings us to our last stop on this excursion, the ratio scale, which must satisfy all the properties of an interval scale plus have true zero. Thus measurements of length or weight or amount satisfy this requirement; two meters is twice as long as one, ten dollars is twice as much as five, twenty pounds is four times five pounds.
Now we have all the necessary theoretical machinery and vocabulary to move on to our next example.
The Olympic Decathlon
The decathlon is a ten-part track event that is multidimensional. There are strength events like discus, speed events like the 100 meter dash, endurance events like the 1,500 meter run, and events, like the pole vault, that stress agility. Of course underlying all of these events is some notion of generalized athletic ability, which may predict performance in all events reasonably accurately.18 How is the decathlon scored? In a word, arbitrarily. Each event is counted “equally” in that an equal number of points is allocated for someone who equaled the world record that existed in that event at the time that the scoring rules were specified.19 How closely one approaches the world record determines the number of points received (i.e., if you are within 90 percent of the world record you get 90 percent of the points). As the world records in separate events change, so too does the number of points allocated. If the world record gets 10 percent better, then 10 percent more points are allocated to that event. Let us examine the two relevant questions: Is this accurate measurement? Is this a fair contest?
To judge the accuracy of the procedure as measurement, we need to know the qualities of the scale so defined. Can we consider decathlon scores to be on a ratio scale? Is an athlete who scores 8,000 points twice as good as someone who scores 4,000? Most experts would agree that such statements are nonsensical. Can we consider decathlon scores to be on an interval scale? Is the difference between an athlete who scores 8,000 and one who scores 7,000 in any way the same as the difference between one who scores 2,000 and another who scores 1,000? Again, experts agree that this is not true in any meaningful sense. But, as we shall see, fairness requires that it needs to be approximately true over the (hopefully narrow) regions in the scale where most of the competitors perform.
How successful have the formulators of the scoring scheme for the Olympic Decathlon been in making this contest fair to athletes of all types?
Can we consider decathlon scores to be ordinally scaled? A fair contest must be. It is certainly so within any one event, but across events it is less obvious. This raises an important and interesting issue: If we are using a test as a contest, and we wish that it be fair, we must gather data that would allow us to test the viability of the requirements stated previously. The most interesting condition is that of transitivity. The condition suggests two possible outcomes in a situation involving multidimensional comparisons:
1. There may exist instances in which person A is preferred to person B and person B to person C, and last, person C is preferred to person A. For example, in any NFL season one can almost always construct a number of sequences in which team A beats team B which then beats team C, which later beats team A. This is called an “intransitive triad,” and, in football at least, it happens sufficiently often that we cannot always attribute it to random fluctuations. It means that in some multidimensional situations, no ordinal scale exists. This is not necessarily a bad thing. In this instance it contributes to the health of the professional football betting industry.
2. Data that allow the occurrence of an intransitive triad are not gathered. This means that while the scaling scheme may fail to satisfy the requirements of an ordinal scale, which are crucial for a fair contest, we will never know. This situation occurs in single-elimination tournaments, as well as in big-choice situations.
In a situation involving big choice, we are prevented from knowing if even the connectedness axiom is satisfied. How can we test the viability of this axiom if we can observe only A on one person and only B on another?
To get a better sense of the quality of measurement represented by the decathlon, let us consider what noncontest uses might be made of the scores. The most obvious use would be as a measure of the relative advantage of different training methods. Suppose we had two competing training methods, for example, one emphasizing strength and the other endurance. We then conduct an experiment in which we randomly assign athletes to one or the other of these two methods. In a pretest we get a decathlon score for each competitor and then again after the training period has ended. We then rate each method's efficacy as a function of the mean improvement in total decathlon score. While one might find this an acceptable scheme, it may be less than desirable. Unless all events showed the same direction of effect, some athletes might profit more from a training regime that emphasizes strength, while others might need more endurance. It seems that it would be far better not to combine scores, but rather to treat the ten component scores separately, perhaps as a profile. Of course each competitor will almost surely want to combine scores to see how much the total has increased, but that is later in the process. The measurement task, in which we are trying to understand the relation between training and performance, is better done at the disaggregated level. It is only for the contest portion that the combination takes place.
We conclude that scoring methods that resemble those used in the decathlon can only be characterized as measurement in an ordinal sense. And thus the measures obtained are only suitable for crude sorts of inferences.
When Is a Contest Fair?
In addition to the requirement of an ordinal scale, fair measurement also requires that all competitors know the rules in advance, that the same rules apply to all competitors equally, and that there is nothing in the rules that gives one competitor an advantage over another because of some characteristic unrelated to the competition. How well do the decathlon rules satisfy these criteria?
Certainly the scoring rules are well known to all competitors, and they apply evenhandedly to everyone. Moreover, the measurements in each event are equally accurate for every competitor. Thus if two competitors throw the shot the same distance, they will get the same number of points. Last, is a competitor placed at a disadvantage because of unrelated characteristics? No; each competitor's score is determined solely by performance in the events. We conclude that the decathlon's scoring rules comprise a fair contest even though they comprise a somewhat limited measuring instrument.
The decathlon represents a good illustration of what can be done with multidimensional tests. Sensible scoring can yield a fair contest, but not good measurement. There has been an attempt to count all events equally, balancing the relative value of an extra inch in the long jump against an extra second in the 1,500 meter run. But no one would contend that they are matched in any formal way. The decathlon is a multidimensional test, but it is not big choice as we have previously defined it. Every competitor provides a score in each event (on every “item”). How much deterioration would result if we add big choice into this mix?
Big choice makes the situation worse. As a real illustration, let us consider a pseudosport that was the subject of a popular 1980s TV program on ABC called Superstars. On it athletes from various sports were gathered together to compete in a series of seven different events. Each athlete had to select five events from among the seven. The winner of each event is awarded ten points, second place seven, third place five, and so on. The overall winner was the one who accumulated the most points. Some events were “easier” than others because fewer or lesser athletes elected to compete in that event; nevertheless the same number of points were awarded. This is big choice by our definition, in that there were events in which some athletes could not compete (e.g., Joe Frazier, a former world champion heavyweight boxer, chose not to compete in swimming because he could not swim). Are the scores in such a competition measurement as is commonly defined? No. Is the contest fair? By the rules of fairness described above, perhaps. Although because some of the data were missing (e.g., how well participants would have done on the events they chose not to compete in) the checking of key underlying assumptions is impossible.
If we are careful we can use big choice in a multidimensional context and under limited circumstances to have fair contests. We cannot yet have measurement in this context at a level of accuracy that can be called anything other than crude. Therefore we do not believe that inferences based on such procedures should depend on any characteristic other than their fairness. This being the case, users of big choice should work hard to assure that their scoring schemes are indeed as fair as they can make them.
When Is It Not Fair?
We might term big choice “easy choice,” because often big choice is really no choice at all. Consider a “choice” item in which an examinee is asked to discuss the plot of either (a) The Pickwick Papers or (b) Crime and Punishment from a Marxist perspective. If the student's teacher chose to include only The Pickwick Papers in the syllabus, there really is no choice. At least the student had no choice, because it was not plausible to answer any but a single option. Thus fairness requires the various options to be of equal difficulty. This returns us to the primary point of this account. How are we to ascertain the relative difficulty of big-choice items?
CONCLUSIONS
Can the uncritical use of choice lead us seriously astray? While there are several sources of evidence summarized in this chapter about the size of choice effects, I focused on just one series of exams, the College Board's Advanced Placement tests. Summaries from other sources, albeit analyzed in several different ways, suggest strongly that the Advanced Placement exams are not unusual. In fact they may be considerably better than average.
Experience with allowing choice in an experimental SAT is instructive.20 It had long been felt by math teachers that it would be better if examinees were allowed to use calculators on the mathematics portion of the SAT. An experiment was performed in which examinees were allowed to use a calculator if they wished. The hope was that it would have no effect on the scores. Alas, calculators improved scores. The experiment also showed that examinees who used more elaborate calculators got higher scores than those who used more rudimentary ones.21 Sadly, a preliminary announcement had already been made indicating that the future SAT-M would allow examinees the option of using whatever calculator they wished or not using one at all.
A testing situation corresponds to measuring people's heights by having them stand with their backs to a wall. Allowing examinees to bring a calculator to the testing situation, but not knowing for sure whether they had one, nor what kind, corresponds to measuring persons for height while allowing them, unbeknownst to you, to bring a stool of unknown and varying height on which to stand. Accurate and fair measurement is no longer possible.
Our discussion has concentrated on explicitly defined choice in tests, or “alternative questions” in the language of the first half of the twentieth century. However, in the case of portfolio assessment, the element of choice is implicit, and not amenable to many of the kinds of analysis that have been described here. Portfolio assessment, another “bright idea” of some educational theorists, may be more or less structured in its demands on the examinee—that is, it may specify the elements of the portfolio more or less specifically. However, to the extent that the elements of the portfolio are left to the choice of the examinee, portfolio assessment more closely resembles ABC's Superstars than even the decathlon. In portfolio assessment, how many forms of the test are created by examinee choice? Often, as many as there are examinees! In this case, such forms cannot be statistically equated. Applicants to universities, or for jobs, present a portfolio of accomplishments. These portfolios must be compared and evaluated so that the candidates can be ordered with respect to their suitability. Is it possible to do this both fairly and well?
Retreating back to the easier question, is building examinee choice into a test possible? Yes, but it requires extra work. Approaches that ignore the empirical possibility that different items do not have the same difficulty will not satisfy the canons of good testing practice, nor will they yield fair tests. But to assess the difficulty of choice items, one must have responses from a random sample of fully motivated examinees. This requires a special sort of data-gathering effort.
What can we do if the assumptions required for equating are not satisfied across the choice items? If test forms are built that cannot be equated, scores comparing individuals on incomparable forms have their validity compromised by the portion of the test that is not comparable. Thus we cannot fairly allow choice if the process of choosing cannot be adjusted away.
Choice is anathema to standardized testing unless those aspects that characterize the choice are irrelevant to what is being tested. Choice is either impossible or unnecessary.
AFTERWORD
The conclusion I reach in this chapter is bleak. Yet the triage task faced by hiring agents or admission officers is very real. Is there anything that provides even a ray of hope? I think so. Specifically,
1. If there are some common elements associated with all applicants (e.g., they all take the same exam), a fair ordering of the applicants can begin with the ordering on that exam.
2. If there are vast differences between candidates on items with choice (e.g., one candidate won an Olympic swimming medal while still in high school whereas her competitor won fourth place in the school's French competition) fair conclusions can be drawn about relative commitment, accomplishment, and proficiency. Mozart was a better musician than I am a swimmer. But the smaller the differences, the less valuable the evidence is for making comparative judgments.
3. Sometimes other issues enter into the decision. Remember the problem that Samantha Stewart, the admissions director, faced at the very beginning of this chapter. Although there was no way for her to be able to tell whether one candidate was a better violinist than the other was a quarterback, the decision was, in the end, easy. The university had desperate need of a quarterback but had plenty of violinists. This solution illustrates an old and honored strategy, usually known as the principle of “It don't make no nevermind.” When faced with a difficult problem you can't solve, find a way to avoid it.
I hope that I have made the case for avoiding, as much as is possible, giving choice. There are enough instances where there is no alternative but to have choice; we should not add to them. Last let me reiterate a point I made earlier—when choice is added, more able subgroups of examinees will choose more wisely than less able subgroups. This has been shown to exacerbate the differences between groups, hardly the outcome hoped for by proponents of providing choice toward the goal of fairer testing.
This chapter developed from H. Wainer and D. Thissen, “On Examinee Choice in Educational Testing,” Review of Educational Research, 64 (1994): 159–195.
1 College Entrance Examination Board 1905.
2 Indeed it challenges the very nature of what we would call a standardized test.
3 The graders for each test were identified, with their institutional affiliations. A practice, if followed in these litigious times, that would make finding people willing to grade exams a task of insuperable difficulty.
4 Section II of the 1921 exam asked the examinee to answer five of twenty-six questions. This alone yielded more than 65,000 different possible “forms.” When coupled with Section III (pick one essay topic from among fifteen) and Section I (“answer 1 of the following 3”) we arrive at the unlikely figure shown in table 6.1.
5 Carl Brigham (1890–1943) was, arguably, the inventor of the SAT.
6 Their warnings are strongly reminiscent of Fermat's marginal comments about his only recently proved theorem.
7 Personal communication, February 10, 1993.
8 Reported by Fremer, Jackson and McPeek (1968).
9 Pomplun et al. 1991; DeMauro 1991.
10 Fitzpatrick and Yen 1993.
11 Powers et al. 1992.
12 Wang, Wainer, and Thissen 1993.
13 An operational administration of these items involving more than 18,000 examinees.
14 Lukhele, Thissen, and Wainer 1994; Wainer and Thissen 1993.
15 Popham 1987.
16 The interested reader can begin with Gregory Cizek's excellent 1993 paper and work backward through the references provided by him.
17 It is not uncommon in education for innovations to be tried without an explicit design to aid in determining the efficacy of the intervention. Harold Gulliksen (personal communication, October 1965) was fond of recounting the response he received when he asked what was the control condition against which the particular educational innovation was to be measured. The response was “We didn't have a control because it was only an experiment.”
18 Actually it only predicts accurately for top-ranked competitors, who tend to perform “equally” well in all events. There are some athletes who are much better in one event or another, but they tend to have much lower overall performance than generalists who appear more evenly talented.
19 The Olympic decathlon scoring rules were first established in 1912 and allocated 1,000 points in each event for a world record performance. These scoring rules have been revised in 1936, 1950, 1964, and 1985. It is interesting to note that the 1932 gold medal winner would have finished second under the current (1985) rules.
20 Lawrence 1992.
21 Note that there is no way to know if the more elaborate calculators helped or if more able students chose such calculators. This uncertainty will always be the case when the students make the decision rather than being placed in one category or the other by some controlled process.
