Consider the following example (“Example 1”). Starting with our usual suppliers relvar S, suppose we define views V1 and V2 as follows:

VAR V1 VIRTUAL ( S WHERE CITY = 'London' OR CITY = 'Paris' ) ;

VAR V2 VIRTUAL ( ( S WHERE CITY = 'London' )
                   UNION
                 ( S WHERE CITY = 'Paris'  ) ) ;

Now, it’s intuitively obvious that these two views are semantically equivalent, even though their definitions—more precisely, their defining expressions—are syntactically distinct. What I mean by this observation is that (to spell the point out) it’s clearly the case that at any given time, those two expressions both denote the same relation. Thus, it’s also intuitively obvious that (a) if Q is a query on either V1 or V2, then Q is defined for the other view as well (and it produces the same result on both), and (b) what’s more, an analogous remark applies to updates also. But I want to take a closer look at part (b) of this claim in particular.

First, then, let’s think about INSERT operations. Suppose we try to insert a tuple for supplier S9 with city London. Then:

Second, DELETE operations. Suppose we try to delete the tuple for supplier S1. Then:

So the claims I made earlier do seem to hold up, at least with respect to this first example. And it’s tempting to conclude that, more generally, if views V1 and V2 are equivalent in the sense illustrated by that example—i.e., if their defining expressions are such that at any given time they both denote the same relation—then if U is an update on either V1 or V2, it must be the case that U is defined for the other one as well, and it has the same effect on both. Indeed, I’m on record^[138] as making a series of rather dogmatic assertions on such matters, all of them along the following lines:

Note: Before I try to elaborate on this “principle”—if principle it truly is—I need to clarify a couple of points. First, with respect to queries, what I said before, in essence, was this: If Q is a query on V1, then that same query Q is defined for V2 as well, and it produces the same result on both. But Q obviously can’t quite be “the same query” for both views, because of course the views have different names. Thus, for example, given views V1 and V2 as defined above for Example 1, if I claim that the query

V WHERE STATUS > 15

is defined for both V1 and V2, what I mean is that the symbol V can sensibly be replaced in that query by either V1 or V2. That’s what I meant when I said the expression Q can be said to represent “the same query” for both views. And given our usual sample values, that query will of course return the same result in both cases:

+-------------------------------+
| SNO | SNAME | STATUS | CITY   |
+-----+-------+--------+--------|
| S1  | Smith |     20 | London |
| S3  | Blake |     30 | Paris  |
| S4  | Clark |     20 | London |
+-------------------------------+

And when I use the phrase “the same update,” of course, I mean it to be understood in the same kind of way.

The second point I need to clarify has to do with what it means, precisely, for two views to be “equivalent.” Of course, I’ve appealed to an intuitive understanding of this notion a couple of times already in this discussion, first in my investigation into Example 1, and then in my attempt to draw a general conclusion from that investigation. But the question is: Is that intuitive understanding sufficient? As you’ve probably guessed already, the answer to this question is no. In fact, much of the rest of this chapter consists of an attempt to pin down much more precisely just what such a notion—i.e., of equivalence of views—might really mean.

Back, then, to the “semantics not syntax principle.” As I’ve indicated, I assumed for a long time that this “principle” obviously made sense. (After all, it certainly makes sense in another context. I refer here to the point, explained in Chapter 2, that compensatory actions aren’t driven by the arbitrary choice of syntax in which the pertinent update happens to have been formulated.) More recently, however, I began to wonder whether it might perhaps not be valid after all, or at best only partly valid. The reasons for this shift in attitude on my part are explained in the next couple of sections, but what they boil down to is this: It’s all too easy to find examples where—on the face of it, at least—such a principle simply doesn’t seem to hold up. What’s more, the machinations that one has to go through in attempts to make it hold up after all get increasingly baroque (epicycles upon epicycles, as it were). All of which makes the following quote from Enrico Bombieri^[139] (one of my favorite quotes, incidentally) increasingly germane: “When things get too complicated, it sometimes makes sense to stop and wonder: Have I asked the right question?” Now read on …

In logic, a tautology is something that’s unconditionally true; more precisely, it’s a predicate whose every possible invocation is guaranteed to yield TRUE, regardless of what arguments are substituted for its parameters if any. For example, p OR NOT p, where p is an arbitrary proposition, is a tautology, and so is 1+1 = 2. (This latter is in fact a proposition, of course, and it doesn’t actually have any parameters.)

Now, tautologies of the form exp1 ≡ exp (where exp1 and exp2 are arbitrary expressions and the symbol “≡” denotes logical equivalence)^[140] are particularly important, because they allow an expression containing an occurrence of exp1 to be rewritten as one containing an occurrence of exp2 instead. To spell the point out, let X1 be an expression containing an occurrence of exp1 as a subexpression; let exp2 be logically equivalent to exp1; and let X2 be the expression obtained from X1 by substituting an occurrence of exp2 for the occurrence of exp1 in question. Then X1 and X2 are logically equivalent in turn; hence, X1 can be rewritten as X2.

By way of illustration, I remind you of Example 1 from the previous section. In that example, I was effectively appealing to the fact that the expression

( S WHERE CITY = 'London' OR CITY = 'Paris' )
  ≡
( ( S WHERE CITY = 'London' ) UNION ( S WHERE CITY = 'Paris' ) )

is a tautology. Note: Of course, I’m sure you’re familiar with all of these ideas, since they form the basis of one of the important things that relational optimizers are supposed to do: namely, expression transformation, sometimes known as “query rewrite.” See SQL and Relational Theory for further discussion.

Now, set theory in general, and as a consequence relational algebra in particular, both include many interesting tautologies of the form discussed above (viz., exp1 = exp). Here are a few relational examples. Let A and B denote arbitrary relational expressions of the same relation type. (In set theory, they would denote arbitrary sets.) Then we have:

A  ≡  A INTERSECT ( A UNION B )

A  ≡  A UNION ( A INTERSECT B )

A INTERSECT B  ≡  A MINUS ( A MINUS B )

A INTERSECT B  ≡  B MINUS ( B MINUS A )

A MINUS B  ≡  A MINUS ( A INTERSECT B )

A UNION B  ≡  ( A MINUS B ) UNION ( A INTERSECT B ) UNION ( B MINUS A )

A MINUS A  ≡  B MINUS B

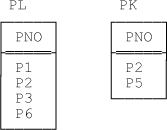
Now let’s consider some implications of the foregoing ideas for the issue of view updating specifically. Consider the following example (“Example 2”), involving relvars PL and PK from Chapters Chapter 9, Chapter 10, and Chapter 11. Just to remind you, those relvars both have just a single attribute PNO (part number), and thus are certainly of the same relation type; relvar PL gives part numbers for parts on sale, and relvar PK gives part numbers for parts in stock. The predicates are thus both very simple:

Sample values are shown in Figure 14-1 (which is extracted from various figures in Chapters Chapter 9, Chapter 10, and Chapter 11).

Figure 14-1. Relvars PL and PK—sample values

Now consider two views, VPL1 and VPL2, whose defining expressions exp1 and exp2 are as indicated here (recall from Chapter 3 that the symbol “” means “is defined as”):

exp1    PL                               /* defining view VPL1 */
exp2    PL INTERSECT ( PL UNION PK )     /* defining view VPL2 */

Observe that the defining expressions exp1 and exp2 here are logically equivalent (i.e., exp1 ≡ exp2 is a tautology—as a matter of fact, it’s a specific illustration of the first tautology in the list I gave above). At any given time, therefore, VPL1 and VPL2 certainly both have the same value; in fact, they both have the same value as the underlying relvar PL does at the time in question. However, now consider the following delete operations:

DELETE ( P2 ) FROM VPL1 ;

DELETE ( P2 ) FROM VPL2 ;

Of course, these two deletes both have the same effect on the target view as such. As you can easily confirm, however, the first causes the P2 tuple to be deleted from relvar PL and has no effect on relvar PK; the second, by contrast, causes that same tuple to be deleted from relvar PL and—at least according to the rules given in Chapters Chapter 9 and Chapter 10 for deleting through intersections and unions—also causes that same tuple to be deleted from relvar PK. So here we apparently have a case where “the same” update on “equivalent” views certainly doesn’t have the same effect (at least, not on the underlying relvars, although as I’ve said it does have the same effect on the views as such).

Now, it’s true that to a user who sees view VPL1 or VPL2 (either one) and the underlying relvars PL and PK as well, the effect of the foregoing deletes on those underlying relvars is at least explicable—assuming the user in question is also aware of the pertinent compensatory actions, of course. But the fact remains that the two deletes do have different effects overall. And the obvious questions remain, too: viz., why do those deletes have different effects overall? And what are the implications of the fact that they do?

Before I try to answer these questions, consider these insert operations on VPL1 and VPL2:

INSERT ( P7 ) INTO VPL1 ;

INSERT ( P7 ) INTO VPL2 ;

Again the effect on the target view is the same in both cases. However, it’s easy to see that the first insert causes a tuple for part P7 to be inserted into relvar PL and has no effect on relvar PK, while the second causes that same tuple to be inserted into relvar PL and—again, at least according to the rules given in Chapters Chapter 9 and Chapter 10 for inserting through intersections and unions—also causes that same tuple to be inserted into relvar PK. Again, then, it seems we have a case where “the same” update on “equivalent” views has different effects, at least on the underlying relvars.

To all of the above, let me add that the problems are compounded by the fact that no possible update on VPL1 has the same effect on the underlying relvars—on relvar PK in particular—as the foregoing delete or insert on VPL2 does.

Clearly, then, there’s something wrong with the “semantics not syntax principle.” Before I try to pin down what it might be, however, I want to consider another related issue.

In SQL and Relational Theory, I briefly describe an implementation technique called semantic optimization. Here’s a simple example, repeated from that earlier book. Consider the expression (SP JOIN S){PNO}. Now, the join here is based on the correspondence between a foreign key in a referencing relvar, SP, and the pertinent target key in the referenced relvar, S. Thus, every SP tuple does join to some S tuple, and every SP tuple therefore does contribute a part number to the projection operation that produces the overall result. So there’s no need to do the join!—the expression can be reduced for evaluation purposes to just SP{PNO}. Note carefully, however, that this transformation is valid only because of the semantics of the situation; with join in general, each operand will include some tuples that have no counterpart in the other and so don’t contribute to the overall result, and transformations such as the one just shown therefore won’t be valid. But in the case at hand, every SP tuple necessarily does have a counterpart in S, because a constraint—actually a foreign key constraint—is in effect that says that every shipment must have a supplier, and so the transformation is valid after all. Terminology: A transformation that’s valid only because a certain constraint is in effect is called a semantic transformation, and the resulting optimization is called a semantic optimization.

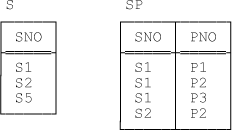
Given the foregoing, now consider the following example (“Example 3”). Suppose for simplicity that relvar S has just one attribute, SNO, and relvar SP has just two attributes, SNO and PNO (so both relvars are in fact “all key”). Figure 14-2 shows some sample values.

Figure 14-2. Relvars S and SP—sample values

Now consider two views, VSP1 and VSP2, whose defining expressions exp1 and exp2 are as indicated here:

exp1    SP                /* defining view VSP1 */
exp2    S JOIN SP         /* defining view VSP2 */

Observe here that (per the foregoing discussion) exp2 can be “semantically transformed” into exp1.^[141] It follows that, at any given time, VSP1 and VSP2 both have the same value; in fact, they both have the same value as the relvar SP does at the time in question. However, now consider the following deletes:

DELETE ( S2 , P2 ) FROM VSP1 ;

DELETE ( S2 , P2 ) FROM VSP2 ;

Once again the two deletes both have the same effect on the views as such. But it’s easy to see that the first causes the tuple (S2,P2) to be deleted from relvar SP and has no effect on relvar S, while the second causes that same tuple to be deleted from relvar SP and—at least according to the rules given in Chapter 8 for deleting through a one to many join—also causes the tuple for supplier S2 to be deleted from relvar S.^[142]

Next, consider the following inserts:

INSERT ( S4 , P1 ) INTO VSP1 ;

INSERT ( S4 , P1 ) INTO VSP2 ;

The first of these inserts fails on a Golden Rule violation (specifically, a violation of the foreign key constraint from SP to S). The second, however, causes the specified tuple to be inserted into relvar SP and—again, at least according to the rules given in Chapter 8 for inserting through a one to many join—also causes a tuple for supplier S4 to be inserted into relvar S. So this time, not only do the updates have different effects on the underlying relvars, they also have different effects on the views as such! In other words, to spell the point out, here we have a situation in which “the same” update doesn’t even have the same effect on its target relvars, even though those target relvars do happen to be “equivalent.”

To all of the above let me add that the problems are compounded by (a) the fact that no possible update on VSP1 has the same effect on the underlying suppliers relvar S as the foregoing delete on VSP2 does and (b) the fact that no possible update on VSP1 has the same effect on either S or VSP1 as the foregoing insert on VSP2 does. What’s more, no possible update on VSP2 produces the same Golden Rule violation on VSP2 as the foregoing (attempted) insert does on VSP1.

Clearly there’s more going on here than meets the eye. We need to take a closer look.

To review briefly (and abstracting somewhat):

So the obvious question in both cases is: Why is B affected at all?

These questions, and others like them, are very vexing. But now let me remind you of that quote from Enrico Bombieri: “When things get too complicated, it sometimes makes sense to stop and wonder: Have I asked the right question?” Maybe “Why is B affected at all?” isn’t the right question to ask. Maybe the right question to ask is: What exactly does it mean for two views—or two view defining expressions, rather—to be equivalent, anyway?^[143]

Well, I think the key to this latter question lies in a careful examination of a concept I’ve been appealing to throughout this book: viz., the notion of information equivalence. Here repeated from Chapter 3 is the definition I originally gave for that concept:

Now, given the foregoing definition, it would appear with respect to Example 2—at least at first sight—that a design consisting of just VPL1 and one consisting of just VPL2 are indeed information equivalent, given that the values of those two relvars are certainly equal at any given time and thus apparently represent the same set of propositions at the time in question. Similarly, it would appear with respect to Example 3 that a design consisting of just VSP1 and one consisting of just VSP2 are also information equivalent, given that the values of those relvars are also equal at any given time. But are these things really so?

For definiteness, let’s focus until further notice on Example 2 and views VPL1 and VPL2. Here again are the view defining expressions:

exp1    PL                               /* defining view VPL1 */
exp2    PL INTERSECT ( PL UNION PK )     /* defining view VPL2 */

Now, it’s true that exp1 and exp2 here are logically equivalent (each can be logically derived from the other). But they aren’t informationally equivalent! To be specific, exp2 tells us something that exp1 doesn’t—it tells us that relvar PK exists, which exp1 certainly doesn’t.^[144] By the same token, consider the tuple consisting of just the PNO value P1, which appears in both relvars. The appearance of that tuple in relvar VPL1 represents the following proposition:

By contrast, the appearance of that same tuple in relvar VPL2 denotes the following proposition:

And just as the expressions exp1 and exp2 are logically but not informationally equivalent, so these two propositions too are logically but not informationally equivalent—i.e., they don’t convey the same information. At the very least, the second proposition tells us it could possibly be the case that part P1 is in stock (a fact about the real world that isn’t even mentioned in the first proposition); likewise, it also tells us that it must be the case that part P1 is either on sale or in stock or both, another fact about the real world that isn’t mentioned in the first proposition.

With the foregoing by way of motivation, I propose the following definition for what it means for two relational expressions to be “informationally equivalent” (except that now I revert to our more usual phrase “information equivalent”):

Clearly, the defining expressions for views VPL1 and VPL2, although they’re logically equivalent, aren’t information equivalent by this definition. Now, our original definition of information equivalence (i.e., for sets of relvars) talked in terms of constraints, not relational expressions—it said two sets of relvars are information equivalent if and only if the pertinent constraints are such that every proposition that can be represented by either set can also be represented by the other. But as we know from numerous discussions and examples earlier in the book, there’s a one to one correspondence between constraints and relational expressions: For every relational expression rx, a constraint whose boolean expression component is IS_EMPTY(rx) can be defined; at the same time, every constraint can always be formulated in terms of such an IS_EMPTY invocation, and so for every constraint there’s a corresponding relational expression. In particular, therefore, as we also know, every view defining expression implies a certain constraint. So we can surely say two such constraints meet the requirements of that original definition (i.e., of information equivalence) if and only if the applicable view defining expressions are information equivalent in the sense just defined.

Now let’s extend these ideas to predicates and propositions. The predicate for VPL1 can be stated symbolically, and slightly more formally, as follows (I’ll use the symbol “⇔” to mean “if and only if”):

t ∊ VPL1  ⇔  t ∊ PL

(“tuple t appears in VPL1 if and only if it appears in PL”). Likewise, the predicate for VPL2 can be stated as follows:

t ∊ VPL2  ⇔  t ∊ PL AND ( t ∊ PL OR t ∊ PK )

(“tuple t appears in VPL2 if and only if it appears in PL and also in either PL or PK”). Now, the point of these reformulations is merely to show that the predicates too can be thought of as containing references to the pertinent relvars—and given that they do, we can apply the notion of information equivalence to them also. In the case at hand, of course, we can see that the predicates we’re talking about here are, again, not information equivalent by the proposed definition. What’s more, it seems reasonable to say that if predicates P1 and P2 are information equivalent, then for every proposition that can be obtained by instantiation from P1, there’s an information equivalent proposition that can be obtained by instantiation from P2 (and vice versa, of course).

Given all of the above, then, it seems to me to make sense to say, with respect to Example 2 specifically, that, appearances to the contrary notwithstanding, a design consisting of just VPL1 and one consisting of just VPL2 aren’t information equivalent after all. And a similar remark applies to Example 3 also: The definition of VSP2 mentions relvar S, which the definition of VSP1 doesn’t, and so a design consisting of just VSP1 and one consisting of just VSP2 aren’t information equivalent. To be more specific, the definition of VSP2 tells us the suppliers relvar exists, which the definition of VSP1 doesn’t.^[145]

To get back to Example 2: As a consequence of the foregoing considerations, it isn’t really even true to say the result of evaluating any given query Q on VPL1 at time T and the result of evaluating that same query Q on VPL2 at that same time T will always be identical. To be specific, the result will of course always be the same relation r in both cases—but the set of tuples in that relation r will represent different sets of propositions in the two cases. A fortiori, therefore, it seems to me entirely reasonable that a given update U on VPL1 at time T and the same update U on VPL2 at that same time T might sometimes have different effects. More particularly, I think it’s perfectly reasonable to say updates on VPL1 never have any effect on relvar PK, while updates on VPL2, by contrast, sometimes do have an effect on that relvar. I even think it’s reasonable in general that the same update might have different effects on two views (on the views as such, I mean), if the corresponding defining expressions are logically equivalent but not information equivalent. In fact, exactly such a situation arose in connection with Example 3, as you’ll surely recall.

The net of all this is as follows: The definition of what it means for two sets of relvars to be information equivalent—see Information Equivalence Revisited—is adequate as it stands. Rather, what needs some refinement is our understanding of what it means for two propositions to be “the same proposition.” I’ve proposed that they be considered the same if and only if they’re information equivalent, and I’ve proposed a definition for this latter concept: viz., they need to be corresponding instantiations of predicates that are information equivalent in turn.

There is, however, still an open question. I’ve proposed that two views V1 and V2 not be regarded as interchangeable if their defining expressions aren’t information equivalent. But the question remains: Are they necessarily interchangeable if their defining expressions are information equivalent? That is, is it possible for an update on V1 and “the same” update on V2 to have different effects, even if the defining expressions for V1 and V2 are information equivalent as defined above? This is a question that I believe deserves further study.

I’d like to close this chapter by offering some observations that show that at least there’s some precedent for the idea that just because expressions exp1 and exp2 appear to be equivalent in certain respects, it doesn’t follow that they can be used completely interchangeably. Note, however, that these remarks are something of a digression from our main topic, and you can skip them if you like.

First of all, I want to make a general point: viz., I strongly suspect that what we’re dealing with here—viz., the issue of updating through “equivalent” expressions—is one of those situation in which the logical difference between values and variables is significant. To be more specific, there’s a logical difference between an expression and a pseudovariable reference:

(See the very end of Chapter 2 if you need to refresh your memory regarding pseudovariables in general, and recall from Chapter 3 that views act as pseudovariables as far as updates are concerned.) In other words, an expression and a pseudovariable reference have very different semantics, even if they’re syntactically identical.

Next, I can recall several occasions in the past where thinking carefully about the logical difference between values and variables led to an epiphany (or what I certainly thought of at the time as an epiphany, anyway). One case in point has to do with the model of type inheritance Hugh Darwen and I were developing, or trying to develop, as a logical consequence of the type theory aspects of The Third Manifesto. We were struggling with the concept of what’s known in the world of object orientation (OO) as substitutability, which OO writings typically explain thus:

For example, if SQUARE is a subtype of RECTANGLE, then it should be possible to substitute squares for rectangles in the foregoing kind of way, because squares are rectangles. Taken at face value, however, this concept seems to give rise to all kinds of absurdities, including squares that aren’t square, circles that aren’t circular, and other such solecisms (contradictions in terms, really).^[147] It was only when we realized that the OO term object sometimes meant a variable and sometimes a value that we also realized that what we needed to do was distinguish between variable substitutability and value substitutability—and it was making that distinction that enabled us to avoid those OO solecisms. To be more specific, it was making that distinction that led us to realize that certain expressions, though they might be interchanged with complete freedom in read-only contexts, could be interchanged only conditionally in update contexts.

My third point also has to do with our inheritance model but is perhaps more obviously related to the question of exactly what it means for two expressions to be equivalent. One of the things I mentioned in the section “Some Well Known Tautologies” was that the expressions A INTERSECT B and A MINUS (A MINUS B) are equivalent—and so indeed they are, inasmuch as they certainly always have the same value. However, it turns out that, first, all expressions have what the Manifesto calls a declared type; second, the declared type of A INTERSECT B isn’t the same, in general, as the declared type of A MINUS (A MINUS B)! To be specific, the declared type of A MINUS (A MINUS B) is the same as that of A, but the declared type of A INTERSECT B is the “least specific common subtype” of the declared types of A and B, which is, in general, some proper subtype of that of A. Once again, therefore, it doesn’t necessarily follow that just because two expressions always have the same value, they can be used interchangeably. In the case at hand, in fact, the two expressions, though they do always have the same value, aren’t even interchangeable for read-only purposes!—at least, not 100 percent.^[148]