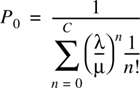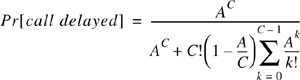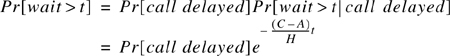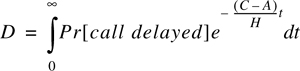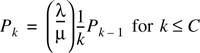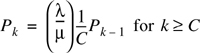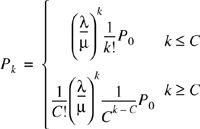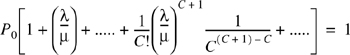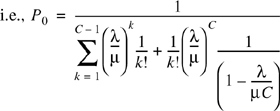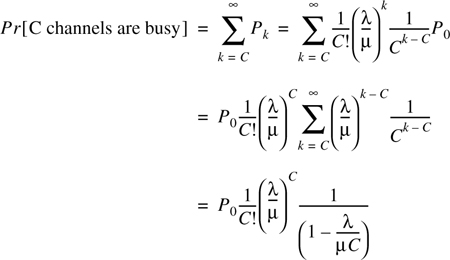Consider a system with C channels and U users. Let λ be the total mean call arrival rate per unit time for the entire trunked system (average number of call requests per unit time over all channels and all users), and let H be the average call holding time (average duration of a call). If A is the offered load for the trunked system, then A = λH.

The probability that a call requested by a user will be blocked is given by

Equation A.2. 

It is assumed that calls arrive according to the Poisson distribution, such that

Equation A.3. 

where a(t) is the number of call requests (arrivals) that have occurred since t = 0 and τ is the call interarrival time (the time between successive call requests). The term λ denotes the average number of call requests per unit time over the user population, and is called the arrival rate.

The Poisson process implies that the time of the nth call arrival and the interarrival times between successive call requests are mutually independent. The interarrival times between call requests are exponential and mutually independent, and the probability that the interarrival time will be less than some time s is given by Pr(τ_n ≤ s) = 1 − e^−λs, s ≥ 0 where τ_n is the interarrival time of the nth arrival, and τ_n = t_{n + 1} − t_n, where t_n is the time at which the nth call request arrived. In other words, the probability density function for τ_n is [Ber92]

Equation A.4. 

For every t ≥ 0, δ ≥ 0,

Equation A.5. 

Equation A.6. 

Equation A.7. 

where O(δ) is the probability of more than one call request arriving over the time interval δ and is a function of δ such that

The probability of n arrivals in δ seconds is found from Equation (A.3)

Equation A.8. 

The user service time is the duration of a particular call that has successfully accessed the trunked system and has been allocated a channel for a call. Service times are assumed to be exponential with mean call duration H, where μ = 1/H is the mean service rate (average number of serviced calls per unit time). H is also called the average holding time. The probability that the service time of the nth serviced call will be less than some call duration s is given by

Equation A.9. 

and the probability density function of the service time is

Equation A.10. 

where s_n is the service time of the nth call.

This trunking system (represented by the Erlang B formula) is called an M/M/C/C queueing system. The first M denotes a memoryless Poisson process for call arrivals, the second M denotes an exponential service time for the users, the first C denotes the number of trunked channels available, and the last C indicates a hard limit on the number of simultaneous users that are served.

The property of Markov chains can be used to derive the Erlang B formula. Consider a discrete time stochastic process that takes values from the set of nonnegative integers, so that the possible states of the process are i = 0, 1,.... The process is said to be a Markov chain if its transition from the present state i to the next state i + 1 depends solely on the state i and not on previous states. Discrete time Markov chains enable the traffic to be observed at discrete observation points for specific traffic conditions. The operation of a practical trunked system is continuous in time, but may be analyzed in small time intervals δ, where δ is a small positive number. If N_k is the number of calls (occupied channels) in the system at time kδ, then N_k may be represented as

Equation A.11. 

where N is a discrete random process representing the number of occupied channels at discrete times. N_k is a discrete time Markov chain with steady state occupancy probabilities which are identical to the continuous Markov chain, and can have values ranging on 0,1,2,....C.

The transition probability P_i,j describes the probability of channel occupancies over a small observation interval, and is given by

Equation A.12. 

Using Equations (A.5) through (A.7), and letting δ → 0, we obtain

Equation A.13. 

Equation A.14. 

Equation A.15. 

Equation A.16. 

Equation A.17. 

The transition state diagram for the Markov chain is shown in Figure A.1

Figure A.1. The transition probabilities represented as a Markov chain state diagram for Erlang B.

Figure A.1 is a Markov chain representation of a trunked system with C channels. To understand the Markov chain state diagram, assume that there are 0 channels being used by the system, i.e., there are no users. Over a small interval of time, the likelihood that the system will continue to use 0 channels is (1 - λδ). The probability that there will be a change from 0 channels to 1 channel in use is given by λδ. On the other hand, if one channel is in use, the probability that the system will transition to 0 used channels is given by μδ. Similarly, the likelihood that the system will continue to use 1 channel is given by 1 − λδ − μδ All of the outgoing probabilities from a certain state sum to 1.

Over a long period of time, the system reaches steady state and has n channels in use. Figure A.2 represents the steady state response of an LCC system.

Figure A.2. A trunked LCC system at steady state with n number of channels in use.

At steady state, the probability of having n channels in use is equivalent to the probability of having (n − 1) channels in use, times the transition probability λδ.

Hence, under steady state conditions,

Equation A.18. 

Equation (A.18) is known as the Global Balance Equation. Furthermore,

Equation A.19. 

Using the Global Balance equation for different values of n, it is seen that

Equation A.20. 

Equation A.21. 

Equation A.22. 

Evaluating Equation (A.20) for different values of n

Equation A.23. 

and

Equation A.24. 

Substituting Equation (A.23) in Equation (A.24)

Equation A.25. 

From Equation (A.23), the probability of blocking for C trunked channels is

Equation A.26. 

Substituting Equation (A.25) in Equation (A.26),

Equation A.27. 

The total offered traffic is A = λH = λ/μ. Substituting this in Equation (A.27), the probability of blocking is given by

Equation A.28. 

Equation (A.28) is the Erlang B formula.

Consider a system where C is the number of trunked channels. The assumptions used to derive the Erlang C formula are similar to those used to derive Erlang B, except for the additional stipulation that if an offered call cannot be assigned a channel, it is placed in a queue which has an infinite length. Each call is then serviced in the order of its arrival, the arrival process obeying a Poisson distribution given by

Equation A.34. 

where a is the number of call arrivals which are waiting for service.

Just as the Erlang B formula was derived using the assumption that all call interarrival times are exponential and independent, the time between successive call arrivals is τ_n = t_{n + 1} − t_n and the distribution of the interarrival times is such that

Equation A.35. 

As was the case for Erlang B, the service time for each user already on the trunked system is assumed to be exponential and is given by

Equation A.36. 

Using discrete time Markov chains with transition probabilities given in Equations (A.12) to (A.17), the Erlang C formula is easily derived. Let P_i,j denote the transition probability of going from state i to state j. The state diagram for the system is shown in Figure A.3.

Figure A.3. The transition probabilities represented as a Markov chain state diagram for Erlang C.

The Erlang C formula is derived by assuming that the trunked system is a M/M/C/D queue, where C denotes the maximum number of simultaneous users and D is the maximum number of calls that may be held in the queue for service. If D is assumed to be infinite, then the system is an M/M/C/∞ queue, commonly referred to as simply M/M/C queue. If D is infinite, then P_k may denote the steady state probability of finding k calls in the system (both served and queued calls). That is,

Equation A.37. 

where N_t is the total number of calls either using or waiting for the system at time t. In steady state, the probability that the system is in state k and makes a transition to state k − 1 in the next transition interval is the same as the probability that the system is in state k − 1 and makes a transition to state k. Thus, from the state diagram shown in Figure A.3,

Equation A.38. 

hence

Equation A.39. 

and

Equation A.40. 

hence

Equation A.41. 

and it follows that

Equation A.42. 

Since 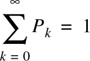, we have

Equation A.43. 

Equation A.44. 

Equation A.45. 

The probability that an arriving call occurs when all C channels are busy and thus has to wait can be determined using Equation (A.42).

Equation A.46. 

The above equation is valid for . Substituting for P_o from Equation (A.45)

Equation A.47. 

But, A = λ/μ = λH. Substituting this in Equation (A.47)

Equation A.48. 

Equation (A.48) is the expression for Erlang C.